CSC 312 Automata Theory Lecture 1 Introduction Administrative













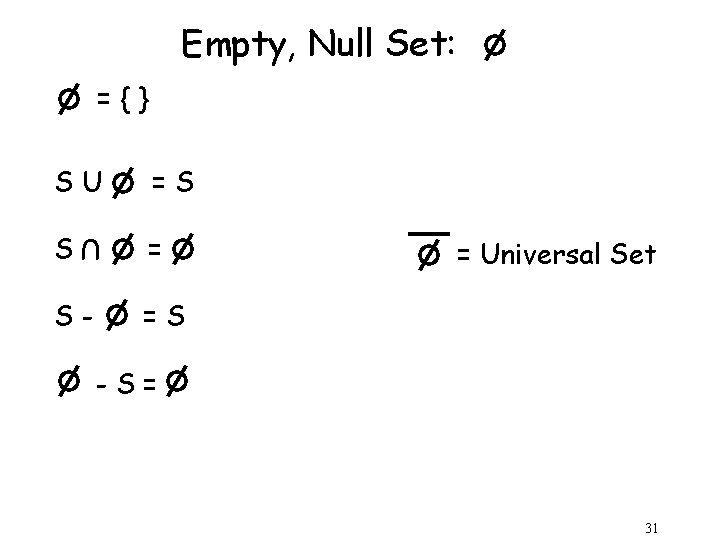





- Slides: 48

CSC 312 Automata Theory Lecture # 1 Introduction

Administrative Stuff • Instructor: Muhammad Usman Akram musmanakram@ciitahore. edu. pk Room # C-11 Web. Link: http: //usman-blog. com/category/courses/theory-ofautomata-fa 15/ • Office Hrs: Mon-Thu 11: 30 – 13: 00 hrs (or by appointment) • Prerequisite: CSC 102 - Discrete Structures

Course Objectives: This course is designed to enable the students to study and mathematically model various abstract computing machines that serve as models for computations and examine the relationship between these automata and formal languages.

Course Outline Regular expressions, TG, DFA and NFAs. Core concepts of Regular Languages and Finite Automata; Moore and Mealy Machines, Decidability for Regular Languages; Non-regular Languages; Transducers (automata with output). Context-free Grammar and Languages; Decidability for Contextfree Languages; Non-context-free Languages; Pushdown Automata, If time allows we will also have a short introduction to Turing machines.

Course Organization Text Book: i) Denial I. A. Cohen Introduction to Computer Theory, Second Edition, John Wiley & Sons. Reference Books: i) J. E. Hopcroft, R. Motwani, & J. D. Ullman Introduction to Automata Theory, Languages, and Computation, Third Edition, Pearson, 2008. Instruments: There will be 3~4 assignments, 3~4 quizzes, Weights: Assignments 10% Quizzes 15% S-I 10% S-II Final Exam 15% 50%

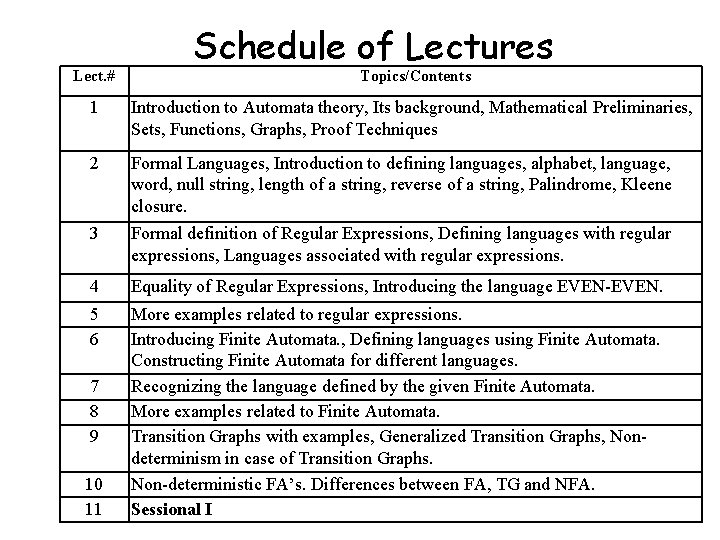
Lect. # Schedule of Lectures Topics/Contents 1 Introduction to Automata theory, Its background, Mathematical Preliminaries, Sets, Functions, Graphs, Proof Techniques 2 Formal Languages, Introduction to defining languages, alphabet, language, word, null string, length of a string, reverse of a string, Palindrome, Kleene closure. 3 Formal definition of Regular Expressions, Defining languages with regular expressions, Languages associated with regular expressions. 4 Equality of Regular Expressions, Introducing the language EVEN-EVEN. 5 6 More examples related to regular expressions. Introducing Finite Automata. , Defining languages using Finite Automata. Constructing Finite Automata for different languages. Recognizing the language defined by the given Finite Automata. More examples related to Finite Automata. Transition Graphs with examples, Generalized Transition Graphs, Nondeterminism in case of Transition Graphs. Non-deterministic FA’s. Differences between FA, TG and NFA. Sessional I 7 8 9 10 11

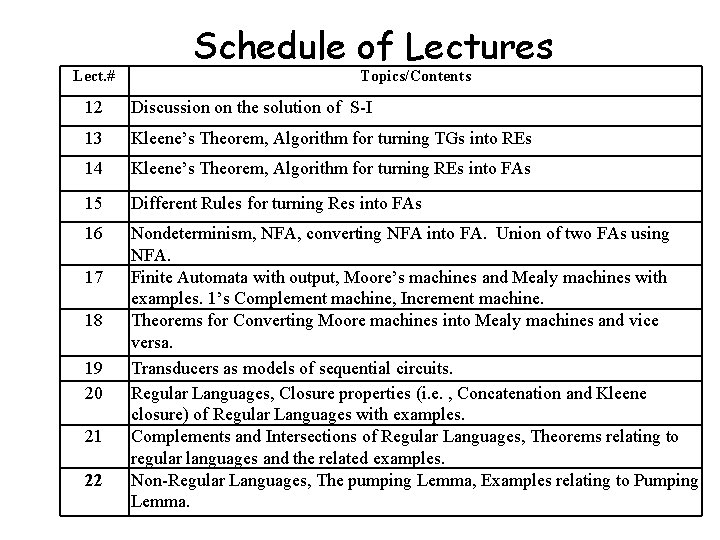
Lect. # Schedule of Lectures Topics/Contents 12 Discussion on the solution of S-I 13 Kleene’s Theorem, Algorithm for turning TGs into REs 14 Kleene’s Theorem, Algorithm for turning REs into FAs 15 Different Rules for turning Res into FAs 16 Nondeterminism, NFA, converting NFA into FA. Union of two FAs using NFA. Finite Automata with output, Moore’s machines and Mealy machines with examples. 1’s Complement machine, Increment machine. Theorems for Converting Moore machines into Mealy machines and vice versa. Transducers as models of sequential circuits. Regular Languages, Closure properties (i. e. , Concatenation and Kleene closure) of Regular Languages with examples. Complements and Intersections of Regular Languages, Theorems relating to regular languages and the related examples. Non-Regular Languages, The pumping Lemma, Examples relating to Pumping Lemma. 17 18 19 20 21 22

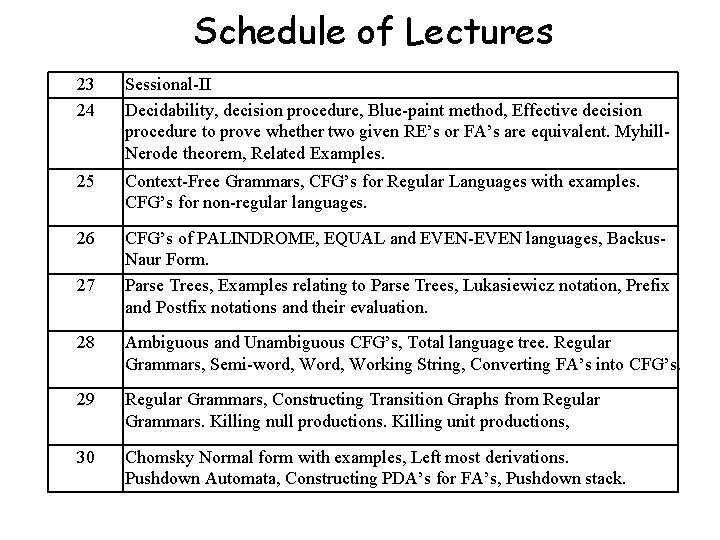
Schedule of Lectures 23 24 Sessional-II Decidability, decision procedure, Blue-paint method, Effective decision procedure to prove whether two given RE’s or FA’s are equivalent. Myhill. Nerode theorem, Related Examples. 25 Context-Free Grammars, CFG’s for Regular Languages with examples. CFG’s for non-regular languages. 26 CFG’s of PALINDROME, EQUAL and EVEN-EVEN languages, Backus. Naur Form. Parse Trees, Examples relating to Parse Trees, Lukasiewicz notation, Prefix and Postfix notations and their evaluation. 27 28 Ambiguous and Unambiguous CFG’s, Total language tree. Regular Grammars, Semi-word, Working String, Converting FA’s into CFG’s. 29 Regular Grammars, Constructing Transition Graphs from Regular Grammars. Killing null productions. Killing unit productions, 30 Chomsky Normal form with examples, Left most derivations. Pushdown Automata, Constructing PDA’s for FA’s, Pushdown stack.

Some basics • Automaton = A self-operating machine or mechanism (Dictionary definition), plural is Automata. • Automata = abstract computing devices • Automata theory = the study of abstract machines (or more appropriately, abstract 'mathematical' machines or systems), and the computational problems that can be solved using these machines. • • Mathematical models of computation Finite automata Push-down automata Turing machines

History • 1930 s : Alan Turing defined machines more powerful than any in existence, or even any that we could imagine – Goal was to establish the boundary between what was and was not computable. • 1940 s/1950 s : In an attempt to model “Brain function” researchers defined finite state machines. • Late 1950 s : Linguist Noam Chomsky began the study of Formal Grammars. • 1960 s : A convergence of all this into a formal theory of computer science, with very deep philosophical implications as well as practical applications (compilers, web searching, hardware, A. I. , algorithm design, software engineering, …)

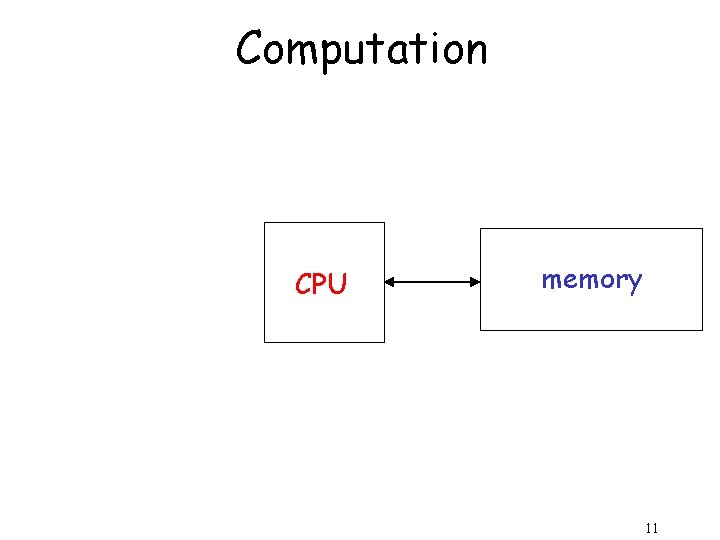
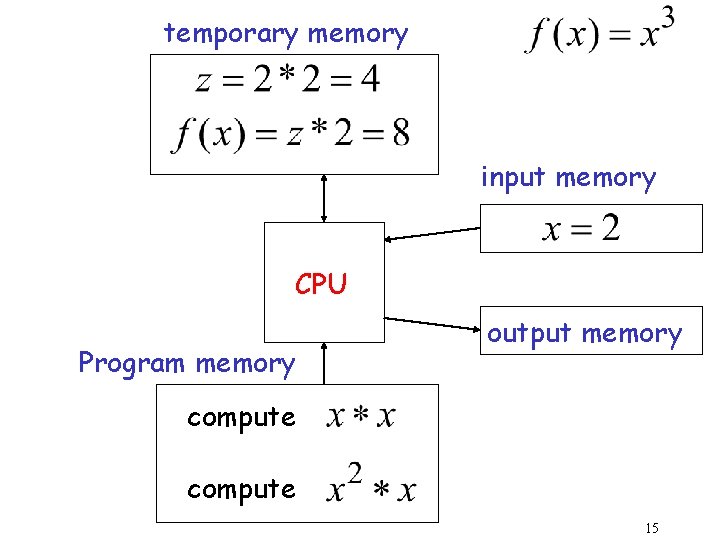
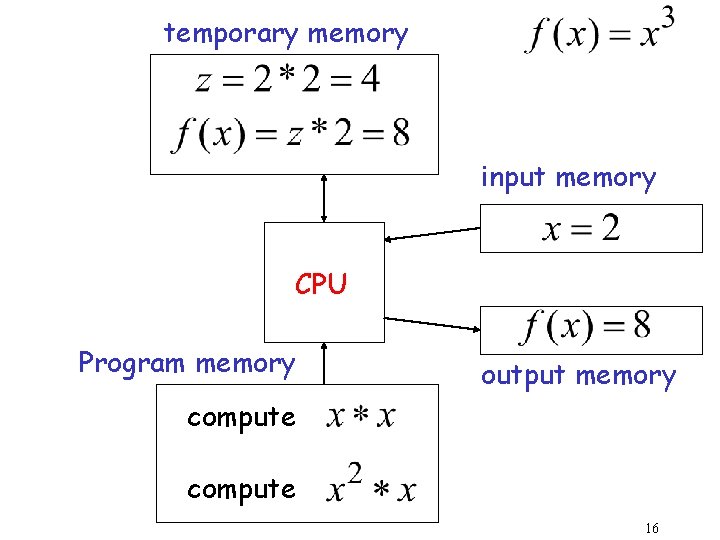
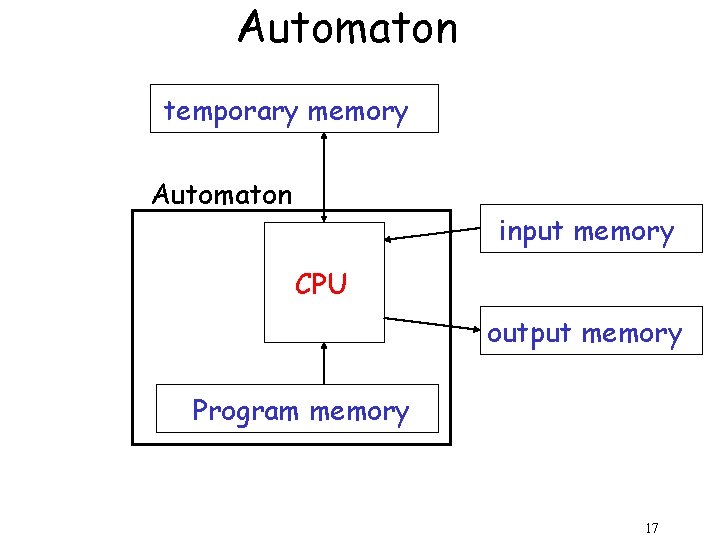
Computation CPU memory 11

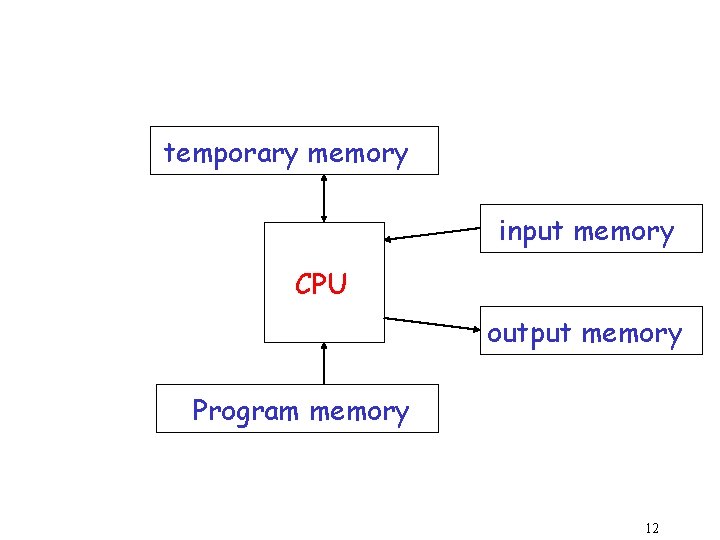
temporary memory input memory CPU output memory Program memory 12

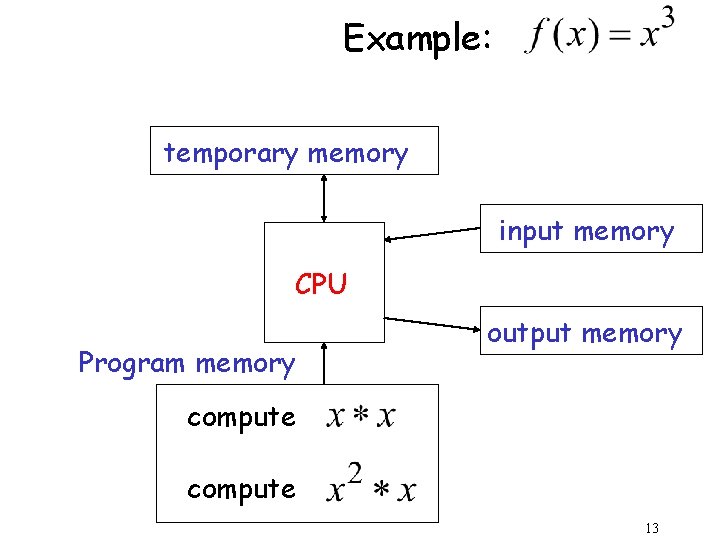
Example: temporary memory input memory CPU Program memory output memory compute 13

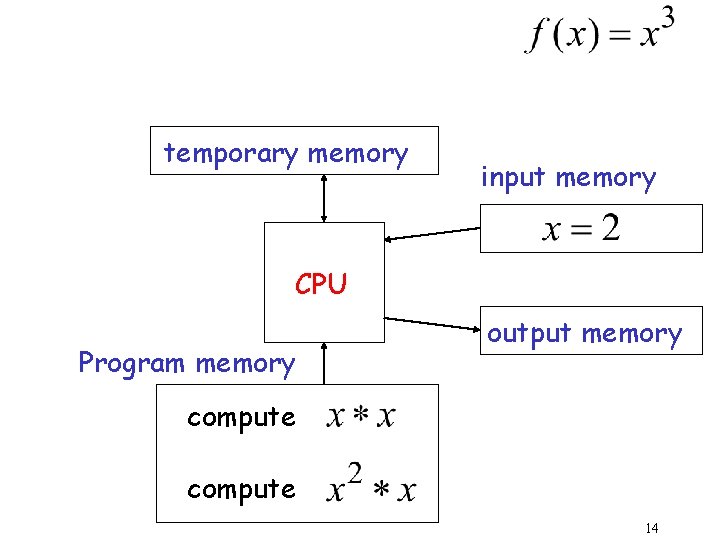
temporary memory input memory CPU Program memory output memory compute 14

temporary memory input memory CPU Program memory output memory compute 15

temporary memory input memory CPU Program memory output memory compute 16

Automaton temporary memory Automaton input memory CPU output memory Program memory 17

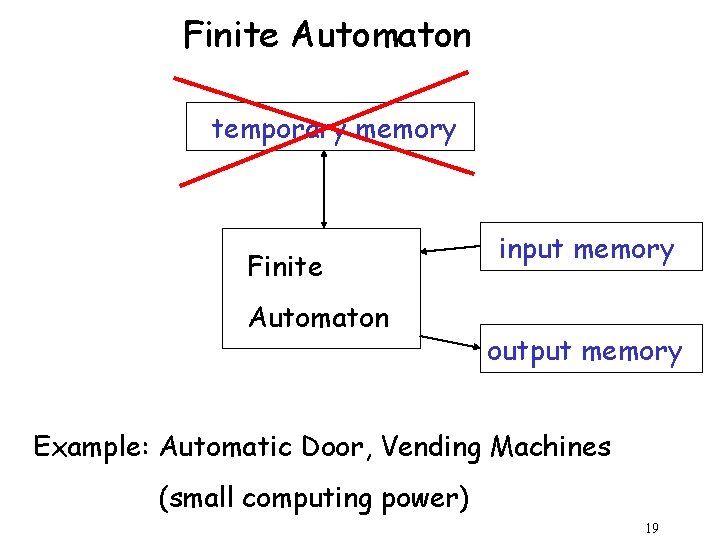
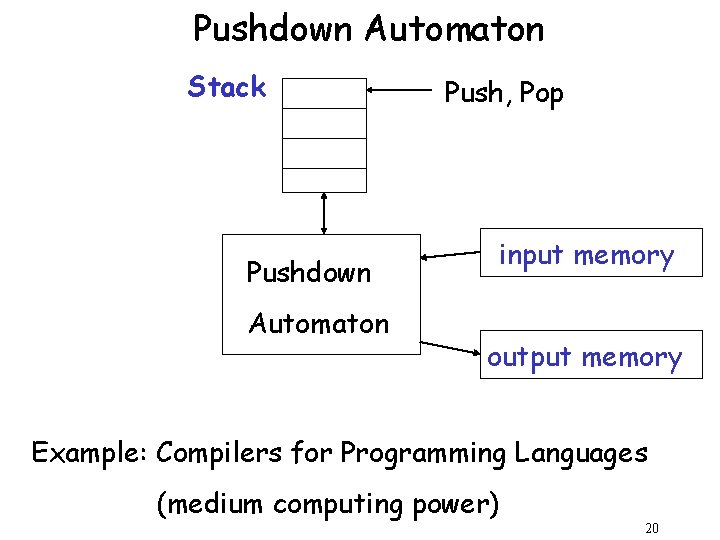
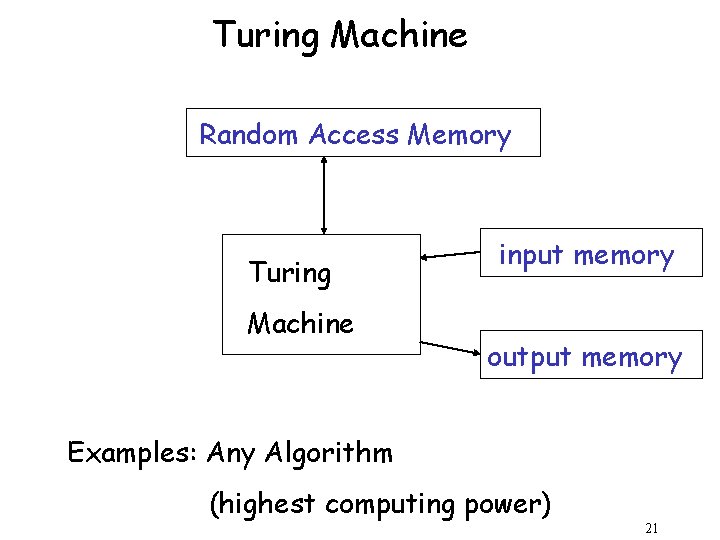
Different Kinds of Automata are distinguished by the temporary memory • Finite Automata: no temporary memory • Pushdown Automata: stack • Turing Machines: random access memory 18

Finite Automaton temporary memory Finite Automaton input memory output memory Example: Automatic Door, Vending Machines (small computing power) 19

Pushdown Automaton Stack Pushdown Automaton Push, Pop input memory output memory Example: Compilers for Programming Languages (medium computing power) 20

Turing Machine Random Access Memory Turing Machine input memory output memory Examples: Any Algorithm (highest computing power) 21

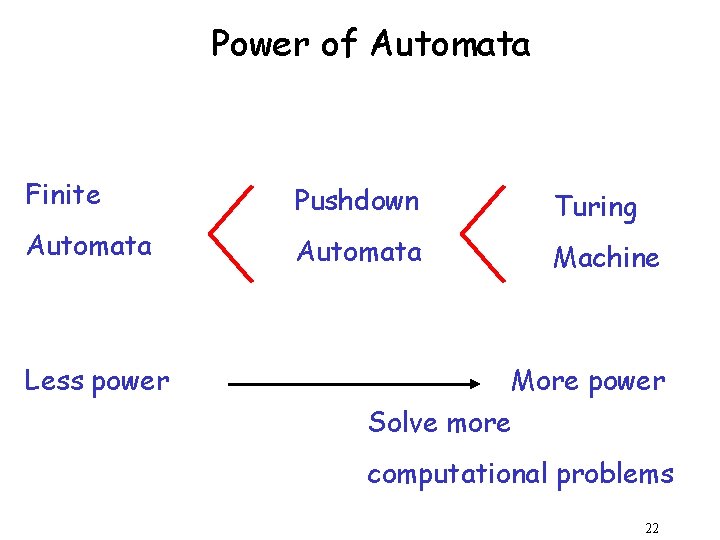
Power of Automata Finite Pushdown Automata Turing Automata Machine Less power More power Solve more computational problems 22

Mathematical Preliminaries • Sets • Functions • Relations • Graphs • Proof Techniques 23

SETS A set is a collection of elements We write 24

Set Representations C = { a, b, c, d, e, f, g, h, i, j, k } C = { a, b, …, k } finite set S = { 2, 4, 6, … } infinite set S = { j : j > 0, and j = 2 k for some k>0 } S = { j : j is nonnegative and even } 25

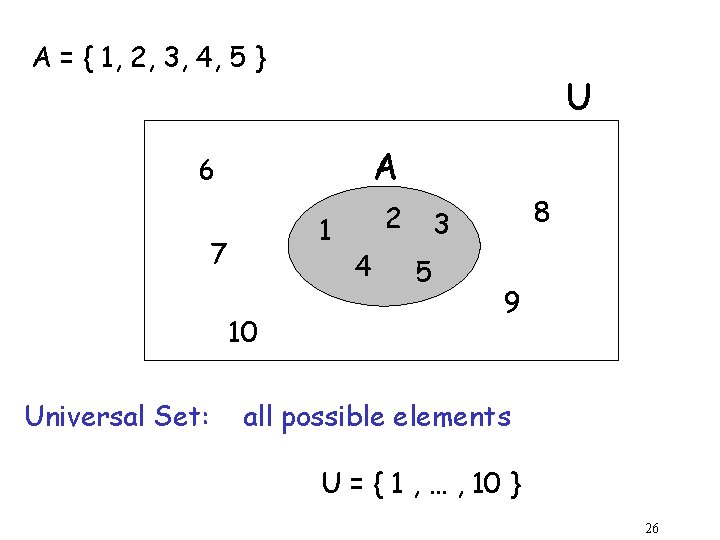
A = { 1, 2, 3, 4, 5 } U A 6 1 7 10 Universal Set: 2 4 8 3 5 9 all possible elements U = { 1 , … , 10 } 26

Set Operations A = { 1, 2, 3 } B = { 2, 3, 4, 5} B A • Union A U B = { 1, 2, 3, 4, 5 } 2 3 1 4 5 • Intersection U A 2 3 B = { 2, 3 } • Difference 1 A-B={1} B - A = { 4, 5 } 4 Venn diagrams 5 27

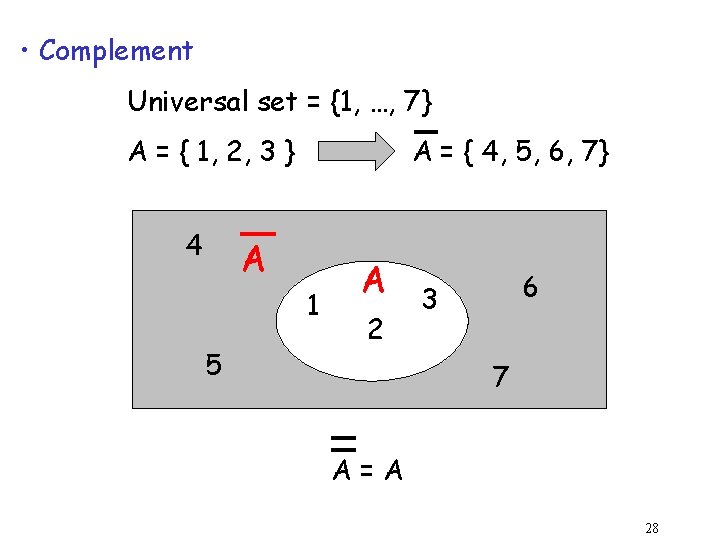
• Complement Universal set = {1, …, 7} A = { 1, 2, 3 } 4 A = { 4, 5, 6, 7} A 1 5 A 2 6 3 7 A=A 28

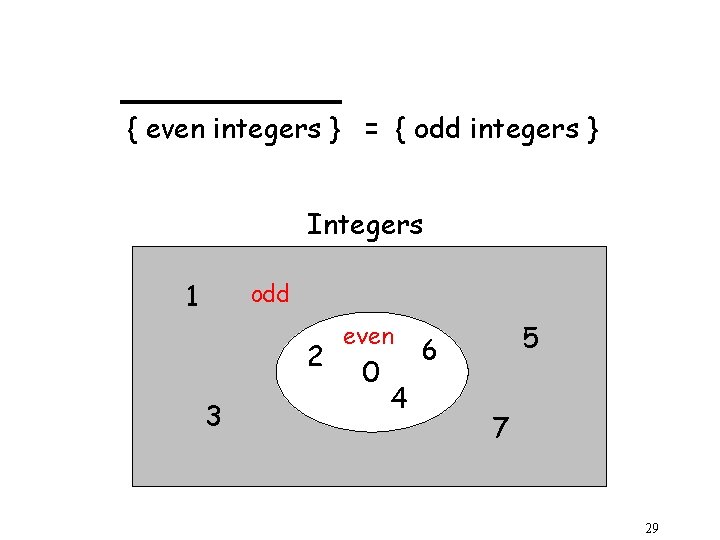
{ even integers } = { odd integers } Integers 1 odd 2 3 even 0 4 5 6 7 29

De. Morgan’s Laws U AUB=A B B=AUB 30
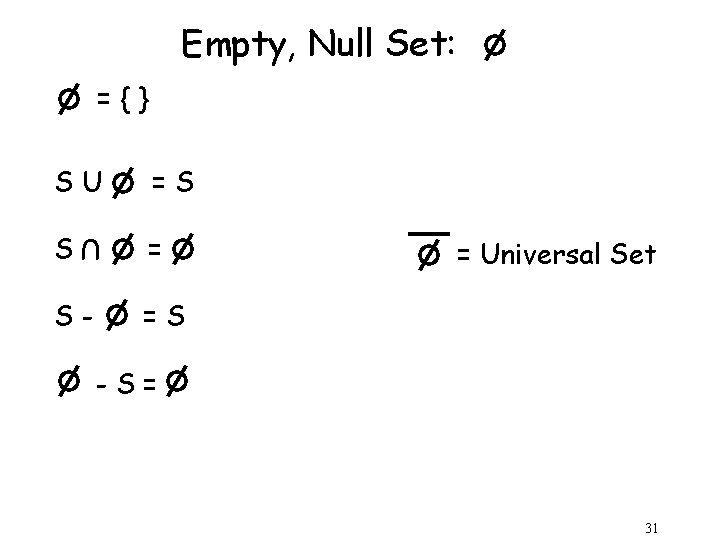
Empty, Null Set: ={} SU =S S = U S- = Universal Set =S -S= 31

Subset A = { 1, 2, 3} B = { 1, 2, 3, 4, 5 } B U Proper Subset: A U A B B A 32

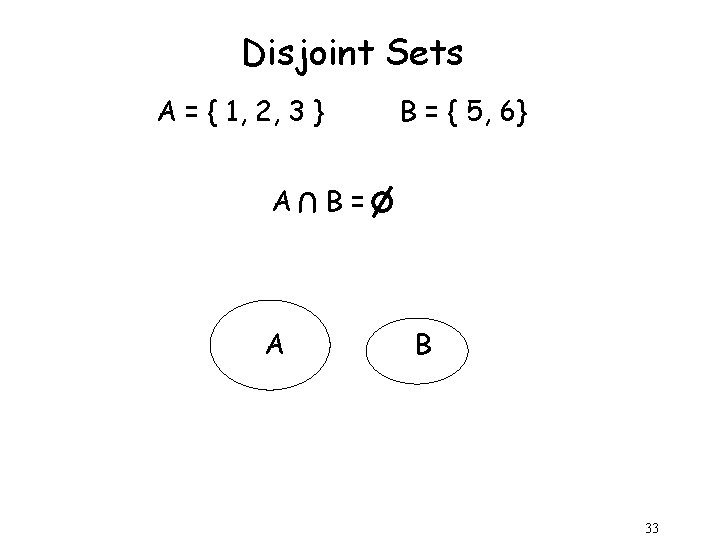
Disjoint Sets A = { 1, 2, 3 } A U A B = { 5, 6} B= B 33

Set Cardinality • For finite sets A = { 2, 5, 7 } |A| = 3 (set size) 34

Powersets A powerset is a set of sets S = { a, b, c } Powerset of S = the set of all the subsets of S 2 S = { , {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c} } Observation: | 2 S | = 2|S| ( 8 = 23 ) 35

Cartesian Product A = { 2, 4 } B = { 2, 3, 5 } A X B = { (2, 2), (2, 3), (2, 5), ( 4, 2), (4, 3), (4, 5) } |A X B| = |A| |B| Generalizes to more than two sets AXBX…XZ 36

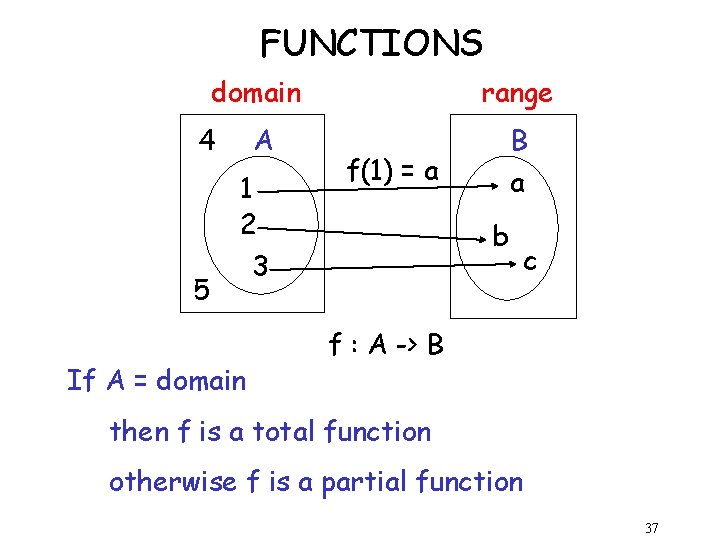
FUNCTIONS domain 4 5 A 1 2 3 If A = domain range B f(1) = a a b c f : A -> B then f is a total function otherwise f is a partial function 37

RELATIONS Let A & B be sets. A binary relation “R” from A to B R = {(x 1, y 1), (x 2, y 2), (x 3, y 3), …} Where and R⊆Ax. B xi R yi to denote e. g. if R = ‘>’: 2 > 1, 3 > 2, 3 > 1 38

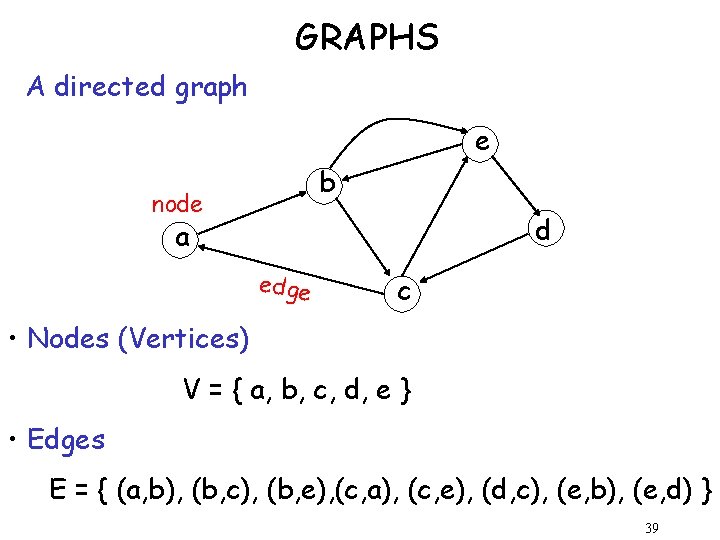
GRAPHS A directed graph e b node d a edge c • Nodes (Vertices) V = { a, b, c, d, e } • Edges E = { (a, b), (b, c), (b, e), (c, a), (c, e), (d, c), (e, b), (e, d) } 39

Labeled Graph 2 6 a b 1 5 3 e 6 2 d c 40

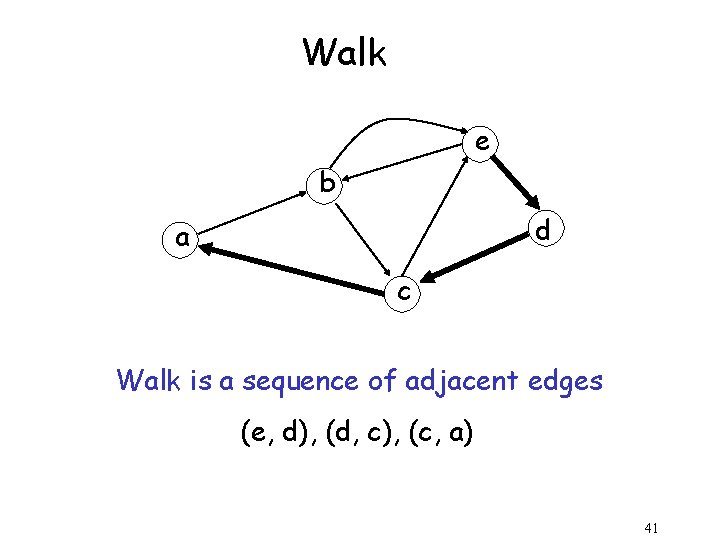
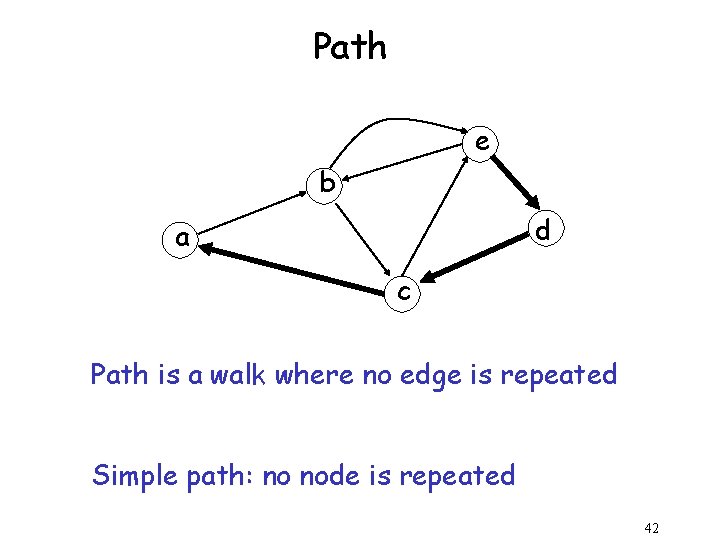
Walk e b d a c Walk is a sequence of adjacent edges (e, d), (d, c), (c, a) 41

Path e b d a c Path is a walk where no edge is repeated Simple path: no node is repeated 42

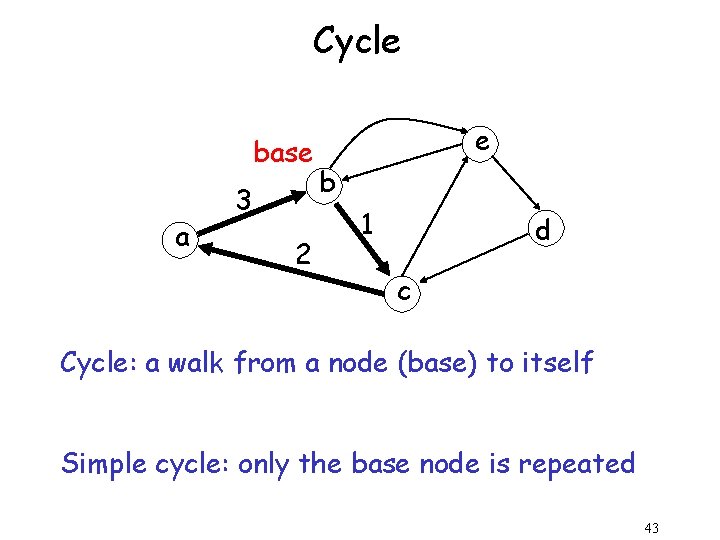
Cycle base a 3 2 e b 1 d c Cycle: a walk from a node (base) to itself Simple cycle: only the base node is repeated 43

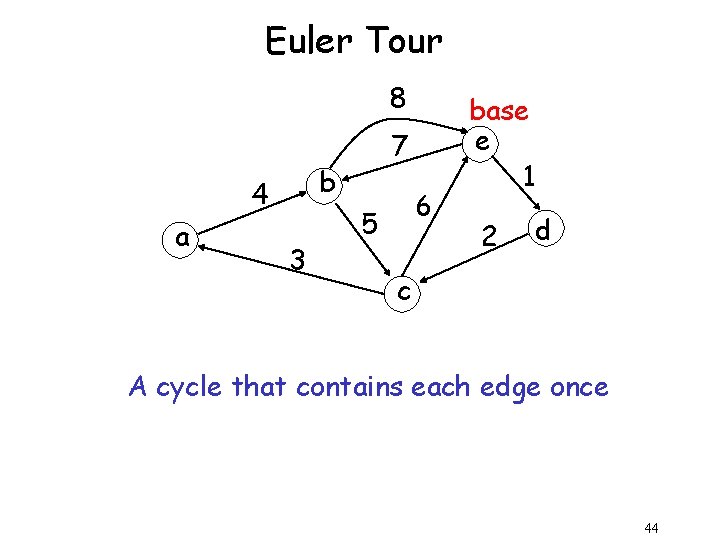
Euler Tour 8 b 4 a 7 3 6 5 base e 1 2 d c A cycle that contains each edge once 44

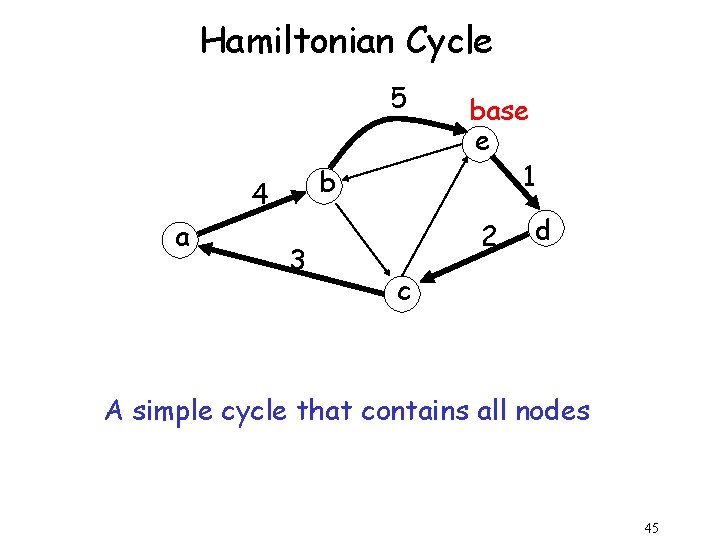
Hamiltonian Cycle 5 b 4 a 3 base e 1 2 d c A simple cycle that contains all nodes 45

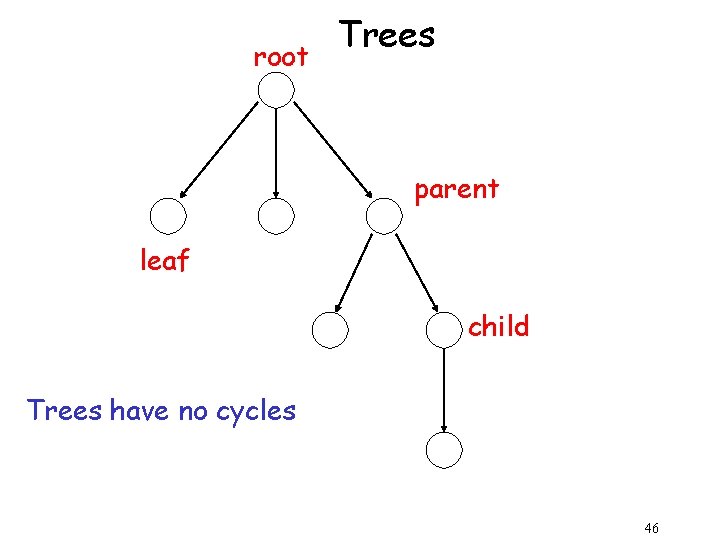
root Trees parent leaf child Trees have no cycles 46

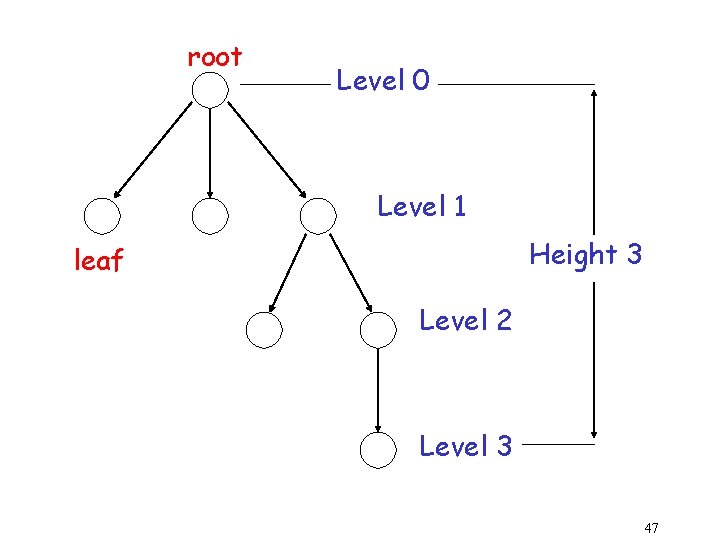
root Level 0 Level 1 Height 3 leaf Level 2 Level 3 47

Binary Trees 48
 01:640:244 lecture notes - lecture 15: plat, idah, farad
01:640:244 lecture notes - lecture 15: plat, idah, farad Administrative theory & praxis
Administrative theory & praxis An introduction to formal languages and automata
An introduction to formal languages and automata Csc102
Csc102 Gtg in theory of automata
Gtg in theory of automata Central concepts of automata theory in flat
Central concepts of automata theory in flat Bidirectional transducers in automata theory
Bidirectional transducers in automata theory Formal languages and automata theory tutorial
Formal languages and automata theory tutorial Automata theory tutorial
Automata theory tutorial Csc3120 datasheet
Csc3120 datasheet Automata theory
Automata theory Automata theory
Automata theory All words
All words Difference between valid and invalid alphabets in automata
Difference between valid and invalid alphabets in automata Csci 3130
Csci 3130 Csci 3130
Csci 3130 Csci3130
Csci3130 Aaaaaabb
Aaaaaabb Why we study automata theory
Why we study automata theory Reverse of a string in automata theory
Reverse of a string in automata theory Csci3130
Csci3130 Cse 312
Cse 312 123 132 213 231 312 321
123 132 213 231 312 321 Nepotism
Nepotism Ics 312
Ics 312 Cse 312
Cse 312 Geog 312 sfu
Geog 312 sfu Java 8 312
Java 8 312 Po box 30512 salt lake city
Po box 30512 salt lake city Cse 332 uw
Cse 332 uw Sophie nam
Sophie nam Altivar 312 solar
Altivar 312 solar 2-312
2-312 Ssis 312
Ssis 312 21 cfr part 312
21 cfr part 312 Bus 312
Bus 312 15 cienmilésimos
15 cienmilésimos Jeopardy adding and subtracting integers
Jeopardy adding and subtracting integers What is the difference between 29 028 and 1 312
What is the difference between 29 028 and 1 312 Ics 312
Ics 312 Ics 312
Ics 312 Ics 312
Ics 312 2/9 simplified
2/9 simplified Bagian dalam sebuah pipa paralon yang berjari jari 21 cm
Bagian dalam sebuah pipa paralon yang berjari jari 21 cm Mcs 312
Mcs 312 Mcs 312
Mcs 312 Ee 312
Ee 312 Mcs 312
Mcs 312 Mcs 312
Mcs 312