CS 6234 Lecture 4 q Linear Programming v

CS 6234: Lecture 4 q Linear Programming v LP and Simplex Algorithm [PS 82]-Ch 2 v Duality [PS 82]-Ch 3 v Primal-Dual Algorithm [PS 82]-Ch 5 v Additional topics: u. Reading/Presentation by students Lecture notes adapted from Comb Opt course by Jorisk, Math Dept, Maashricht Univ, Hon Wai Leong, NUS (CS 6234, Spring 2009) Page 1 Copyright © 2009 by Leong Hon Wai

Combinatorial Optimization Chapter 3 of [PS 82] Duality Combinatorial Optimization Masters OR

LP in general form min s. t. c´ x a´i x xj ≥ xj = bi ≤ bi 0 free jεN iεM i ε M´ j ε N´ 1. Introduce surplus variables for inequality constraints 2. Replace free variables by two non-negative variables. Combinatorial Optimization Masters OR

In standard form… min s. t. c~´ x~ A~ x~ = b x~ ≥ 0 where A~ has extra columns for x´s in N´, and for slack variables, x~ has extra variables for x´s in N´ and for slack variables, c~ has extra elements for x´s in N´. Combinatorial Optimization Masters OR

Starting the dual The simplex method gives an optimal solution x 0~ to the LP in standard form, with a basis Q, satisfying c~´ – (c. B~´ B~-1)A~ ≥ 0. Thus, π´ = c. B~´ B~-1 is a feasible solution to the problem π´ A~ ≤ c~´ where π ε Rm. Combinatorial Optimization Masters OR

The dual 1. π´ Aj ≤ cj, for j ε N, 2. π´ Aj ≤ cj, for j ε N´, and π´ Aj ≤ –cj, for j ε N´, and hence π´ Aj = cj, for j ε N´. 3. –πi ≤ 0, for i ε M´, or πi ≥ 0, for i ε M´. Objective: max π´ b. Combinatorial Optimization Masters OR

Definition of the Dual Definition 3. 1: Given an LP in general form, called the primal, the dual is defined as follows Primal Dual Min c´x Max π´b a ´i x = b i iεM πi free a ´i x ≥ b i i ε M´ πi ≥ 0 xj ≥ 0 jεN π´ Aj ≤ cj xj free j ε N’ π´ Aj = cj Combinatorial Optimization Masters OR

Strong duality Theorem 3. 1: If an LP has an optimal solution, so does its dual, and at optimality their costs are equal. Proof. Let x and π be optimal solutions to the primal and the dual resp. , then c´x ≥ π´Ax ≥ π´b. From the dual (*) From the primal Combinatorial Optimization Masters OR

Strong duality proof Thus the primal has cost at least as high as the dual. Then, if the primal has a feasible solution, the cost of the dual cannot be unbounded. It has feasible solution π´, and since it is not unbounded, it must have an optimum. The cost of π´ is π´ b = c. B~´ B~-1 b = c. B~´ x 0~ which is the optimal solution of the primal. Together with (*) this suffices to prove the Theorem. Combinatorial Optimization Masters OR

The dual of the dual Theorem 3. 2. The dual of the dual is the primal. Proof. Left as an exercise. Theorem 3. 3: Given a primal-dual pair, either of the following holds: 1. Both have a finite optimum 2. Both are infeasible 3. One is unbounded the other is infeasible Proof. Skip. Combinatorial Optimization Masters OR

Complementary slackness Theorem 3. 4: A pair, x, π, respectively feasible in a primal-dual pair is optimal if and only if: ui = πi (a´i x - bi) = 0 vj = (cj - π´ Aj) xj = 0 for all i for all j. Combinatorial Optimization Masters OR (1) (2)

Complementary slackness (2) Proof: Recall ui = πi (a´i x - bi) & vj = (cj - π´Aj) xj Define u = ui (≥ 0) & v = vj (≥ 0) Thus, u = 0 if and only if (1) holds (each ui = 0) and v = 0 if and only if (2) holds (each vj = 0). Now, notice that (u + v) = c´x – π´b. Thus, if (1) and (2) hold, (u + v) = 0, and c´x = π´b. This implies that x and π have the same objective value, and hence are both optimal. Combinatorial Optimization Masters OR

Complementary slackness (3) Consequences: If an inequality constraint in the dual is not binding, then the corresponding primal variable must have value zero and vice versa. Likewise, if a nonnegative variable has strictly positive value, then the corresponding constraint must be binding. Combinatorial Optimization Masters OR

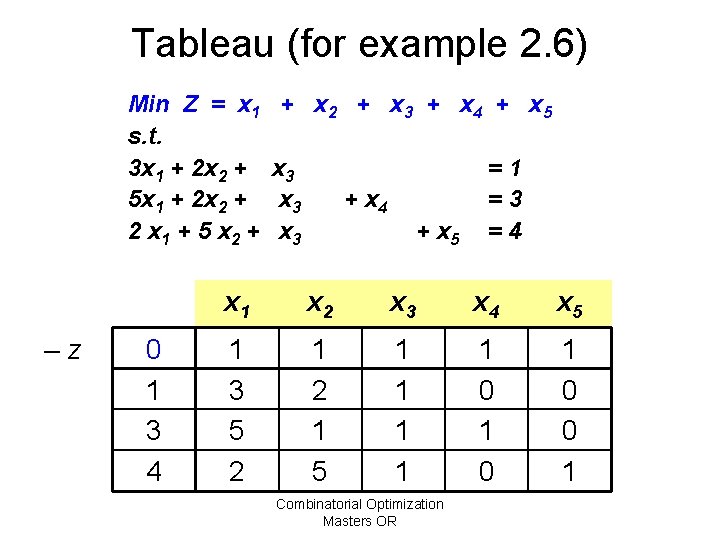
Tableau (for example 2. 6) Min Z = x 1 s. t. 3 x 1 + 2 x 2 + 5 x 1 + 2 x 2 + 2 x 1 + 5 x 2 + –z 0 1 3 4 + x 2 + x 3 + x 4 + x 5 x 3 x 3 + x 4 + x 5 =1 =3 =4 x 1 x 2 x 3 x 4 x 5 1 3 5 2 1 5 1 1 1 0 1 0 0 1 Combinatorial Optimization Masters OR

Simplex Algorithm (Tableau Form) –z x 1 x 2 x 3 x 4 x 5 0 1 1 1 3 2 1 0 0 3 5 1 1 1 0 4 2 5 1 0 1 x 2 x 3 x 4 x 5 –z -6 -3 -3 0 0 0 x 3 = 1 3 2 1 0 0 x 4 = 2 2 -1 0 x 5 = 3 -1 3 0 0 1 Diagonalize to get bfs { x 3, x 4, x 5 } x 1 x 2 x 3 x 4 x 5 –z 0 1 1 1 x 3 = 1 3 2 1 0 0 x 4 = 2 2 -1 0 x 5 = 3 -1 3 0 0 1 Determine reduced cost by making c~j = 0 for all basic col Combinatorial Optimization Masters OR

Combinatorial Optimization Masters OR

Farkas Lemma Skip 3. 3 Combinatorial Optimization Masters OR

The shortest path problem and its dual Definition 3. 3 Given a directed graph G=(V, E) and a nonnegative weight cj ≥ 0 associated with each arc ej ε E, an instance of the shortest path problem (SP) is the problem of finding a directed path from a distinguished source node s to a distinguished terminal node t, with the minimum total weight. Combinatorial Optimization Masters OR

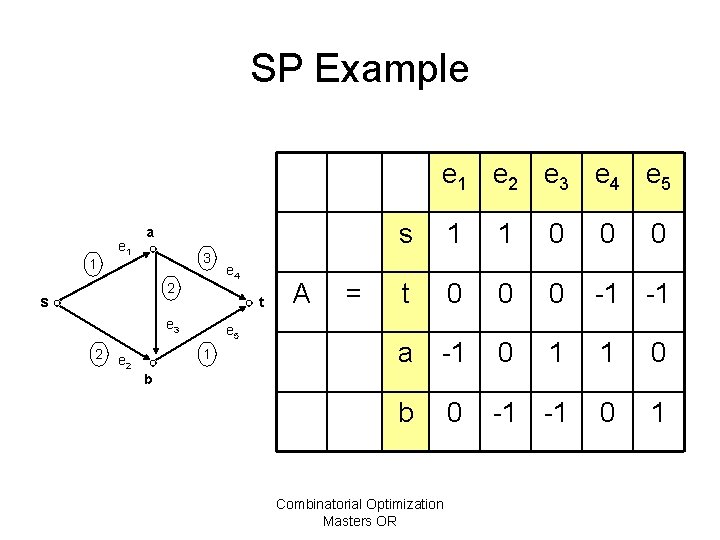
Shortest path problem Feasible set F is given by F = {P = (ej 1, . . , ejk) : P is a directed path from s to t in G}. Cost c(P) = Σi=1 k cji. Formulation as LP uses node-arc incidence matrix A: aij = { 1 -1 0 if arc j leaves node i -f arc j enters node i otherwise Combinatorial Optimization Masters OR

SP Example e 1 e 2 e 3 e 4 e 5 1 e 1 a 3 2 s t e 3 2 e 5 1 e 2 e 4 A = s 1 1 0 0 0 t 0 0 0 -1 -1 a -1 0 1 1 0 b 0 -1 -1 0 1 b Combinatorial Optimization Masters OR

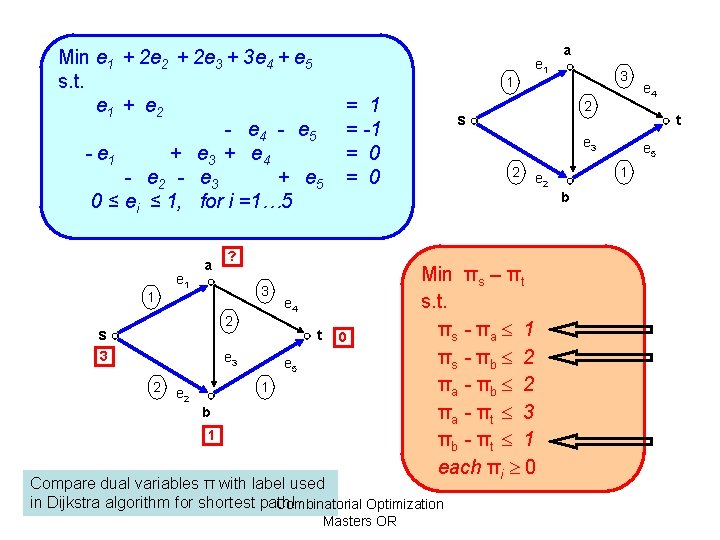
LP formulation Min e 1+ 2 e 2+ 2 e 3 + 3 e 4 + e 5 s. t. e 1 + e 2 - e 1 e 3 + - e 2 0 ≤ ei ≤ 1, i =1… 5 Combinatorial Optimization Masters OR - e 4 e 5 = 1 = -1 = 0

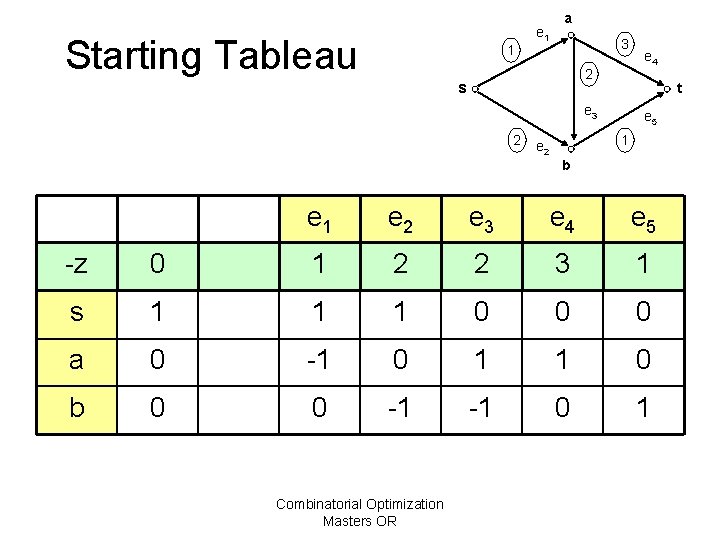
Redundancy Claim: Any solution that satisfies 3 of the four constraints, satisfies all 4 of them. Easily checked. Thus, we omit the constraint for the sink t. Next, we consider the tableau of a feasible solution Combinatorial Optimization Masters OR

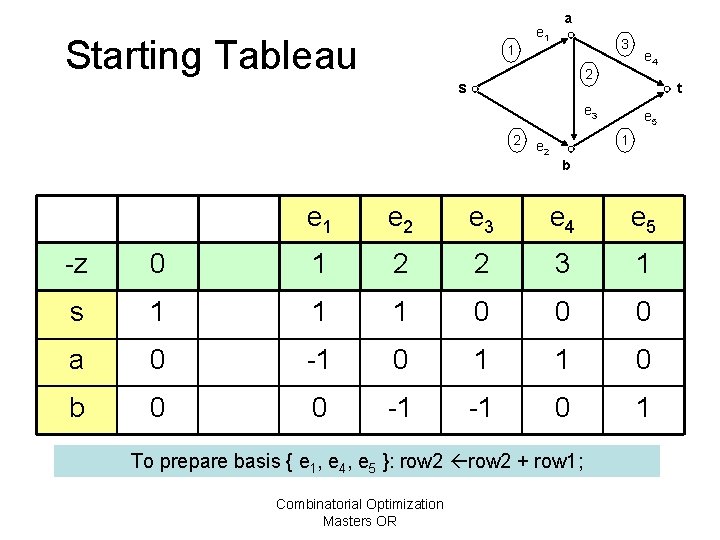
Starting Tableau 1 e 1 a 3 2 s t e 3 2 e 4 e 5 1 e 2 b e 1 e 2 e 3 e 4 e 5 -z 0 1 2 2 3 1 s 1 1 1 0 0 0 a 0 -1 0 1 1 0 b 0 0 -1 -1 0 1 Combinatorial Optimization Masters OR

Summary of LP for SP • Simplex algorithm in tableau form – Cost vector c is also included as a constraint (Read details in [PS 82]-Ch-2) • Each basis has (n-1) edges; Clever idea! – Not all are positive; – Edges with +ve flows are on the (s-t) path • Pivoting – bring in a new edge; – Based on relative cost (row 0 of tableau) Combinatorial Optimization Masters OR

Starting Tableau 1 e 1 a 3 2 s t e 3 2 e 4 e 5 1 e 2 b e 1 e 2 e 3 e 4 e 5 -z 0 1 2 2 3 1 s 1 1 1 0 0 0 a 0 -1 0 1 1 0 b 0 0 -1 -1 0 1 To prepare basis { e 1, e 4, e 5 }: row 2 + row 1; Combinatorial Optimization Masters OR

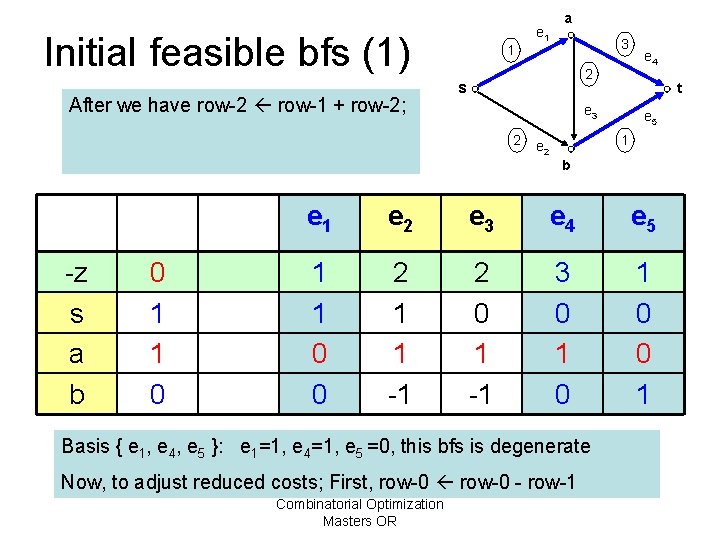
Initial feasible bfs (1) After we have row-2 row-1 + row-2; 1 e 1 a 3 2 s t e 3 2 e 4 e 5 1 e 2 b -z s a b 0 1 1 0 e 1 e 2 e 3 e 4 e 5 1 1 0 0 2 1 1 -1 2 0 1 -1 3 0 1 0 0 1 Basis { e 1, e 4, e 5 }: e 1=1, e 4=1, e 5 =0, this bfs is degenerate Now, to adjust reduced costs; First, row-0 - row-1 Combinatorial Optimization Masters OR

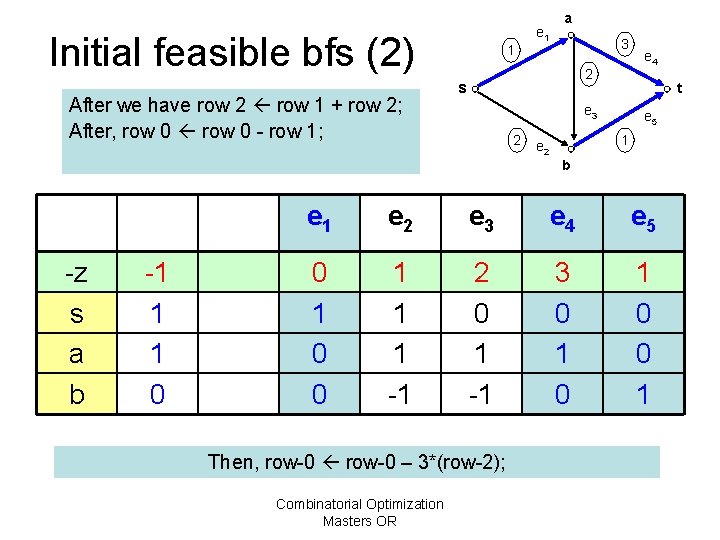
Initial feasible bfs (2) After we have row 2 row 1 + row 2; After, row 0 - row 1; 1 e 1 a 3 2 s t e 3 2 e 4 e 5 1 e 2 b -z s a b -1 1 1 0 e 1 e 2 e 3 e 4 e 5 0 1 0 0 1 1 1 -1 2 0 1 -1 3 0 1 0 0 1 Then, row-0 – 3*(row-2); Combinatorial Optimization Masters OR

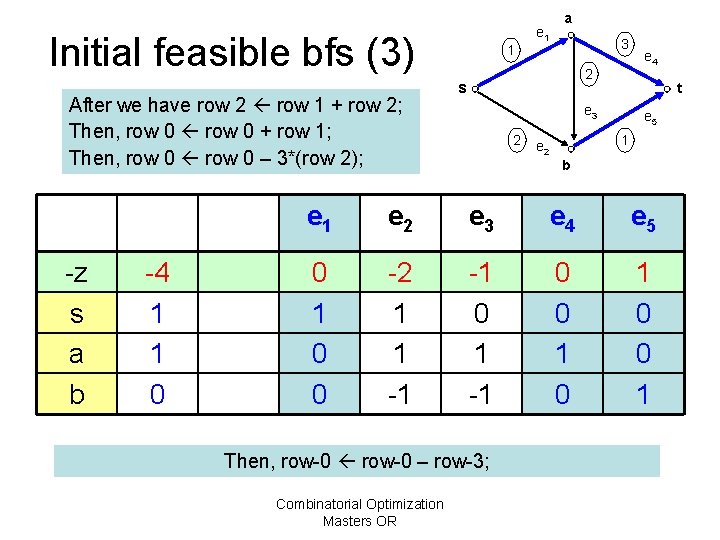
Initial feasible bfs (3) After we have row 2 row 1 + row 2; Then, row 0 + row 1; Then, row 0 – 3*(row 2); -z s a b -4 1 1 0 1 e 1 a 3 2 s t e 3 2 e 4 e 5 1 e 2 b e 1 e 2 e 3 e 4 e 5 0 1 0 0 -2 1 1 -1 -1 0 0 1 Then, row-0 – row-3; Combinatorial Optimization Masters OR

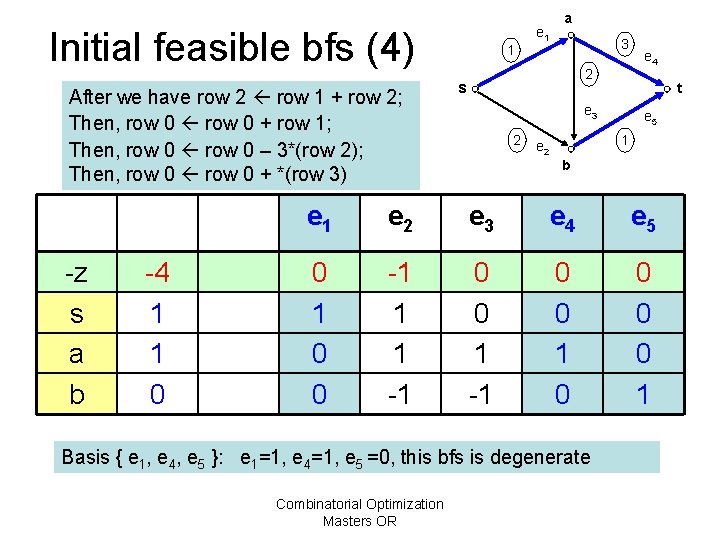
Initial feasible bfs (4) After we have row 2 row 1 + row 2; Then, row 0 + row 1; Then, row 0 – 3*(row 2); Then, row 0 + *(row 3) -z s a b -4 1 1 0 1 e 1 a 3 2 s t e 3 2 e 4 e 5 1 e 2 b e 1 e 2 e 3 e 4 e 5 0 1 0 0 -1 1 1 -1 0 0 1 Basis { e 1, e 4, e 5 }: e 1=1, e 4=1, e 5 =0, this bfs is degenerate Combinatorial Optimization Masters OR

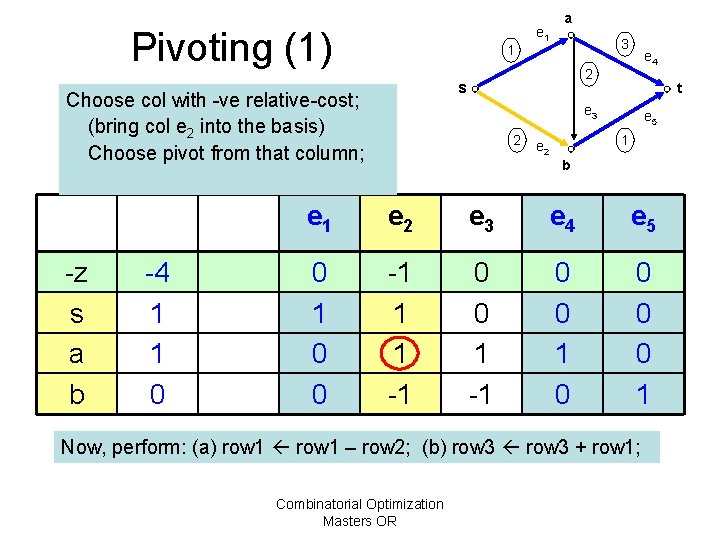
Pivoting (1) 1 -4 1 1 0 3 e 4 2 s Choose col with -ve relative-cost; (bring col e 2 into the basis) Choose pivot from that column; -z s a b e 1 a t e 3 2 e 5 1 e 2 b e 1 e 2 e 3 e 4 e 5 0 1 0 0 -1 1 1 -1 0 0 1 Now, perform: (a) row 1 – row 2; (b) row 3 + row 1; Combinatorial Optimization Masters OR

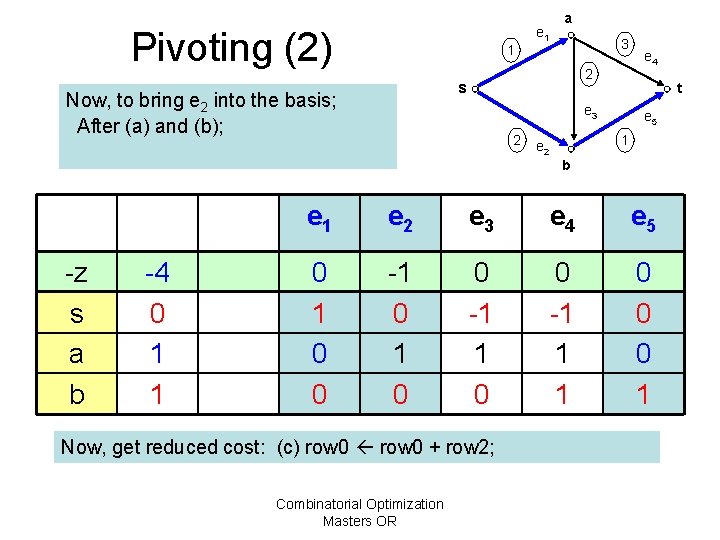
Pivoting (2) 1 e 1 a 3 2 s Now, to bring e 2 into the basis; After (a) and (b); t e 3 2 e 4 e 5 1 e 2 b -z s a b -4 0 1 1 e 2 e 3 e 4 e 5 0 1 0 0 -1 1 1 0 0 0 1 Now, get reduced cost: (c) row 0 + row 2; Combinatorial Optimization Masters OR

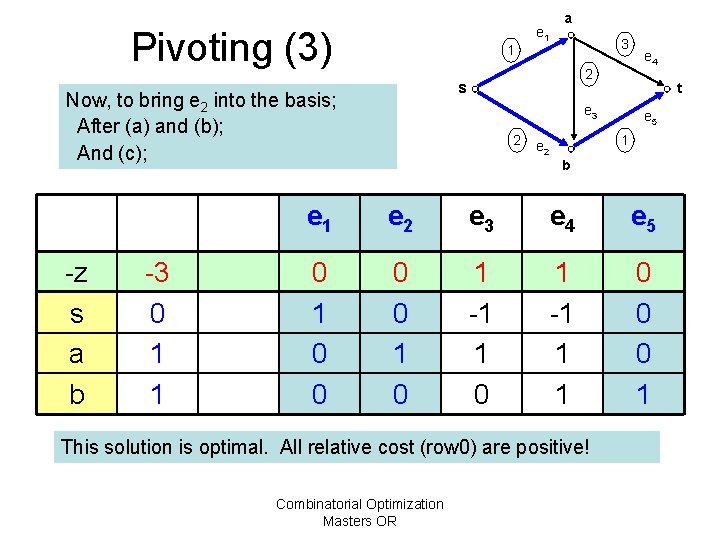
Pivoting (3) 1 -3 0 1 1 3 2 s Now, to bring e 2 into the basis; After (a) and (b); And (c); -z s a b e 1 a t e 3 2 e 4 e 5 1 e 2 b e 1 e 2 e 3 e 4 e 5 0 1 0 1 -1 1 1 0 0 0 1 This solution is optimal. All relative cost (row 0) are positive! Combinatorial Optimization Masters OR

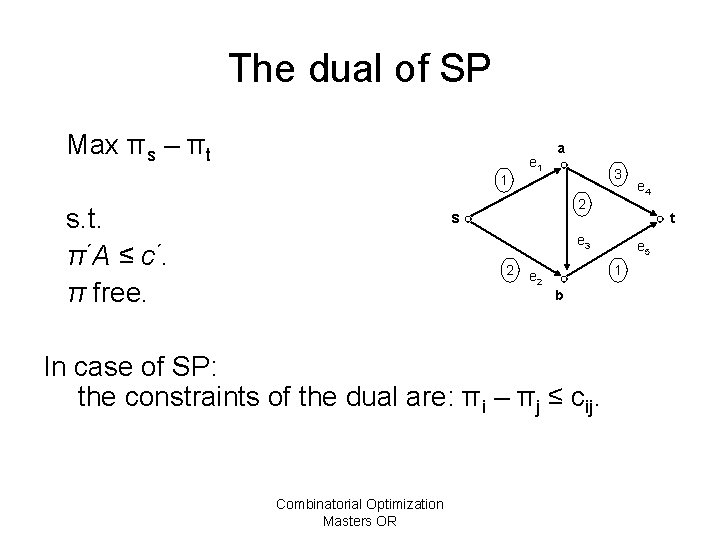
The dual of SP Max πs – πt 1 s. t. π ´A ≤ c ´. π free. e 1 a 3 2 s t e 3 2 b In case of SP: the constraints of the dual are: πi – πj ≤ cij. Combinatorial Optimization Masters OR e 5 1 e 2 e 4

Complementary slackness for SP A path f as defined by primal variables, and an assignment of dual variables π are jointly optimal if and only if: 1. A primal variable with positive value corresponds to a dual constraint that is satisfied at equality. 2. A dual constraint not satisfied at equality corresponds to a primal variable with value zero. Combinatorial Optimization Masters OR

Min e 1 + 2 e 2 + 2 e 3 + 3 e 4 + e 5 s. t. e 1 + e 2 - e 4 - e 5 - e 1 + e 3 + e 4 - e 2 - e 3 + e 5 0 ≤ ei ≤ 1, for i =1… 5 1 e 1 a 2 3 0 e 5 1 e 2 3 2 s 2 b 1 Min πs – πt s. t. πs - πa 1 πs - πb 2 πa - πt 3 πb - πt 1 each πi 0 Compare dual variables π with label used in Dijkstra algorithm for shortest path! Combinatorial Optimization Masters OR e 5 1 e 2 e 4 t e 3 b e 4 t e 3 2 = 1 = -1 = 0 ? 3 s 1 e 1 a

Read up the following sections on your own. Sect 3. 5: Dual Info in the Tableau Sect 3. 6: Dual Simplex Algorithm Sect 3. 7: Intrepretation of Dual Simplex Algorithm Combinatorial Optimization Masters OR

Some Suggested Exercises: All from [PS 82] • • • Theorem 3. 3 3 11 12 13 17 Combinatorial Optimization Masters OR

Thank you. Q&A Hon Wai Leong, NUS (CS 6234, Spring 2009) Page 38 Copyright © 2009 by Leong Hon Wai