CS 1321 CS 1321 Introduction to Programming Georgia

CS 1321

CS 1321: Introduction to Programming Georgia Institute of Technology College of Computing Lecture 21 November 06, 2001 Fall Semester

Today’s Menu 1. Graphs: A brief review 2. Representing Graphs in Scheme 3. Searching Graphs: DFS 4. Searching Graphs: BFS 5. Traversing Graphs: Finding a Path 6. Traversing Graphs: Finding a “short” path.

A Brief Note Believe it or not, you have a test next week. The cut off for material will be Graphs.

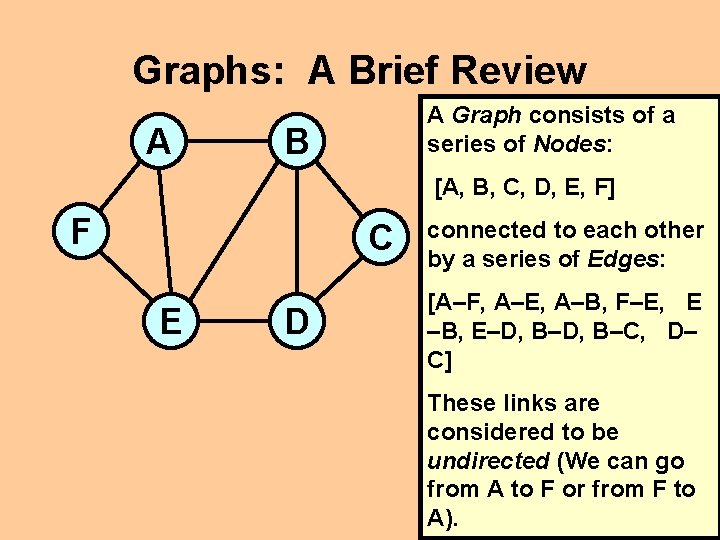
Graphs: A Brief Review A A Graph consists of a series of Nodes: B [A, B, C, D, E, F] F C E D connected to each other by a series of Edges: [A–F, A–E, A–B, F–E, E –B, E–D, B–C, D– C] These links are considered to be undirected (We can go from A to F or from F to A).

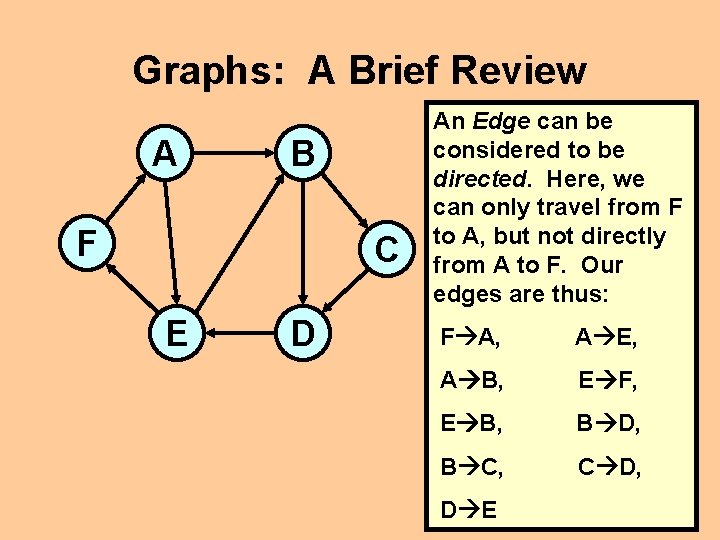
Graphs: A Brief Review A B F C E D An Edge can be considered to be directed. Here, we can only travel from F to A, but not directly from A to F. Our edges are thus: F A, A E, A B, E F, E B, B D, B C, C D, D E

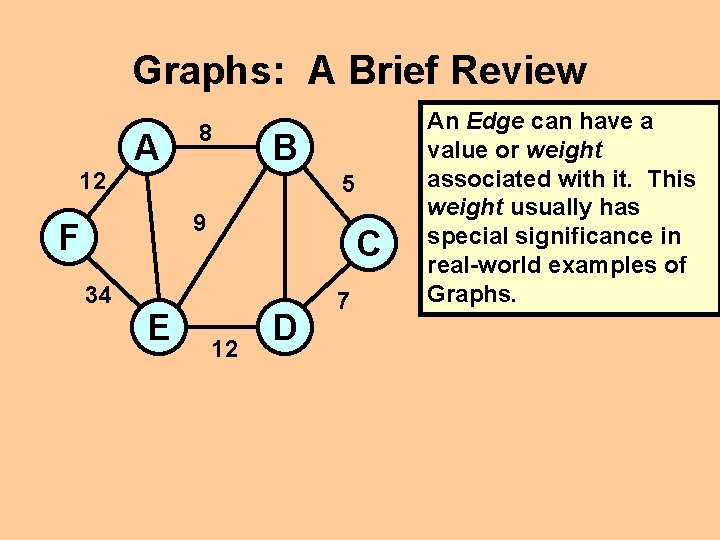
Graphs: A Brief Review 12 A 8 B 5 9 F 34 E C 12 D 7 An Edge can have a value or weight associated with it. This weight usually has special significance in real-world examples of Graphs.

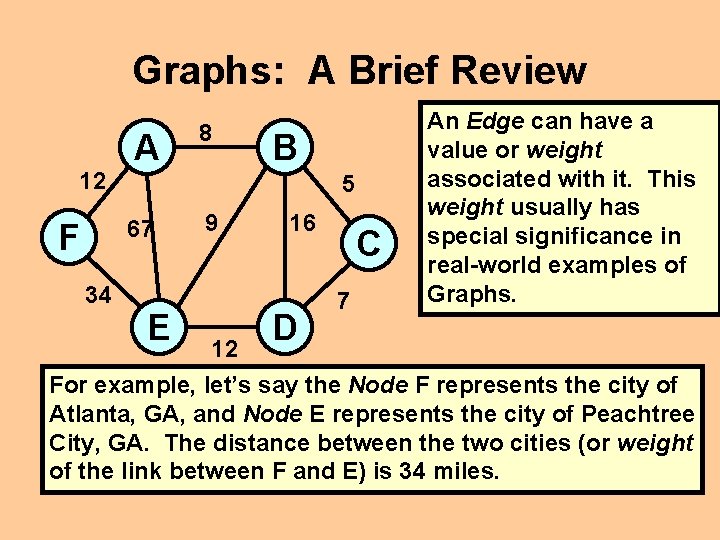
Graphs: A Brief Review 12 A 34 B 5 67 F 8 E 9 16 D C 7 An Edge can have a value or weight associated with it. This weight usually has special significance in real-world examples of Graphs. 12 For example, let’s say the Node F represents the city of Atlanta, GA, and Node E represents the city of Peachtree City, GA. The distance between the two cities (or weight of the link between F and E) is 34 miles.

Working With Graphs: a note before we begin Most of the examples of working with graphs that we’ll go over today will be shown at an algorithmic and graphical level. However, when code is shown, the data definitions that we use may change as our problems grow more and more complex.

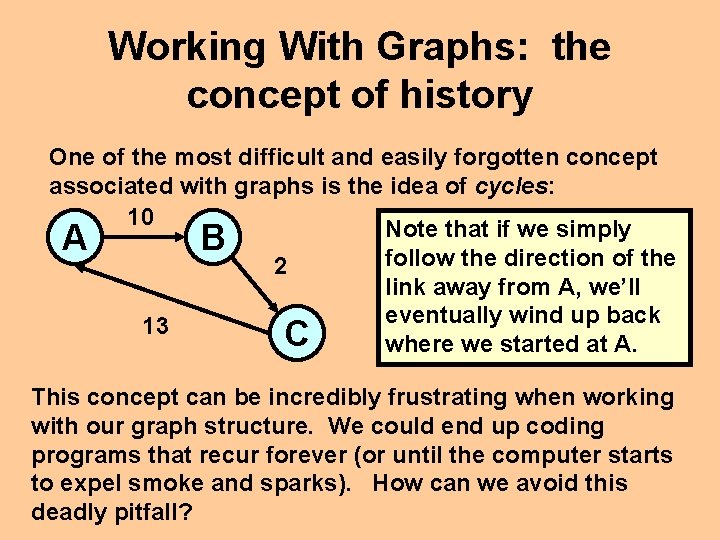
Working With Graphs: the concept of history One of the most difficult and easily forgotten concept associated with graphs is the idea of cycles: 10 Note that if we simply A B 13 2 C follow the direction of the link away from A, we’ll eventually wind up back where we started at A. This concept can be incredibly frustrating when working with our graph structure. We could end up coding programs that recur forever (or until the computer starts to expel smoke and sparks). How can we avoid this deadly pitfall?

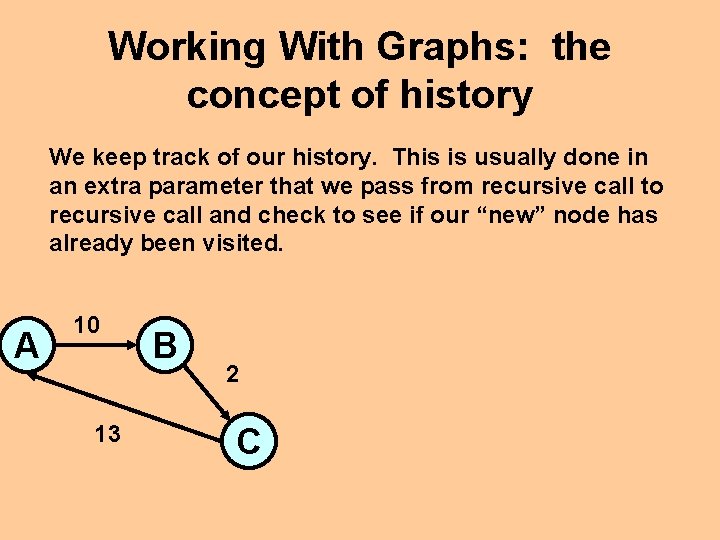
Working With Graphs: the concept of history We keep track of our history. This is usually done in an extra parameter that we pass from recursive call to recursive call and check to see if our “new” node has already been visited. A 10 13 B 2 C

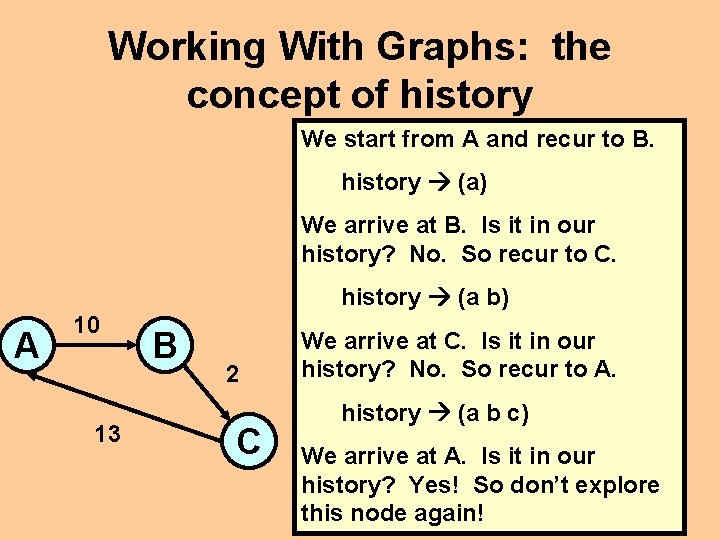
Working With Graphs: the concept of history We start from A and recur to B. history (a) We arrive at B. Is it in our history? No. So recur to C. history (a b) A 10 13 B 2 C We arrive at C. Is it in our history? No. So recur to A. history (a b c) We arrive at A. Is it in our history? Yes! So don’t explore this node again!

Searching Graphs: Depth First Search (review) Given a node in our graph, a list of nodes we’ve visited, and a data value to look for: 1) Check to see if we’ve already visited the current node. Return failure if we have. 2) Check to see if the current node contains the value we’re looking for. Return success if it does. 3) Check to see if we’ve got any place left to search (any links coming off the current node). Return failure if we don’t. 4) Add the current node to our list of nodes we’ve visited and try out each path leading off the current node until one of them succeeds or all of them fail.

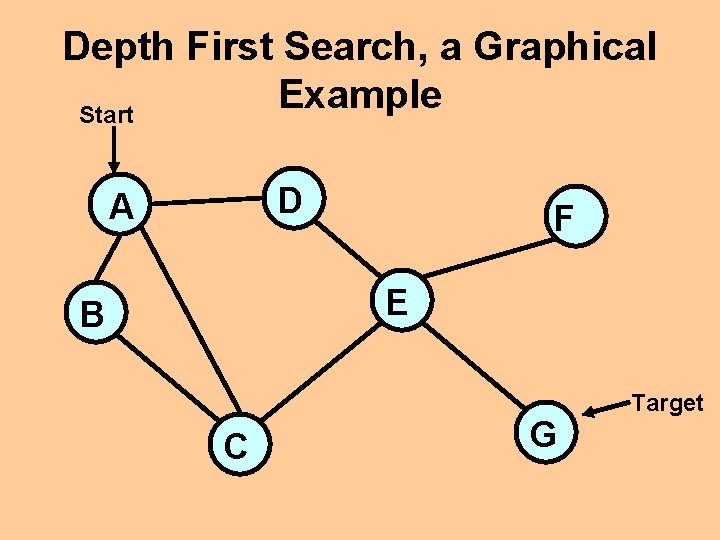
Depth First Search, a Graphical Example Start D A F E B C G Target

Searching Graphs: Breadth First Search Before we begin discussing Breadth First Search, we have to introduce one simple concept first: Queues. The easiest way to understand Queues is to think of a line at a bank or a movie theater. This line has a front end a back end. When new people arrive, they are added to the back of the line (no cutting!). When the bank teller or cashier is ready, they help the person at the front of the line. That’s it. Now, in CS terminology:

Queues A queue is a FIFO data definition: First thing into the queue is the first thing out of the queue. You enqueue items onto the back of your queue. You dequeue items from the front of your queue.

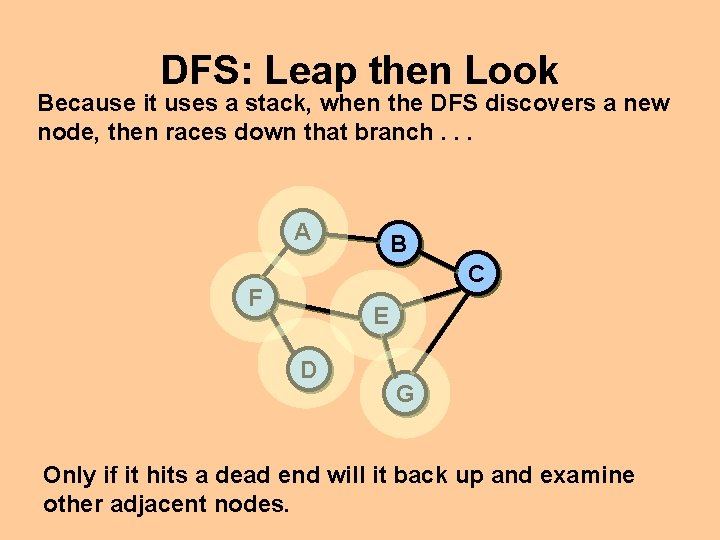
DFS: Leap then Look Because it uses a stack, when the DFS discovers a new node, then races down that branch. . . A B C F E D G Only if it hits a dead end will it back up and examine other adjacent nodes.

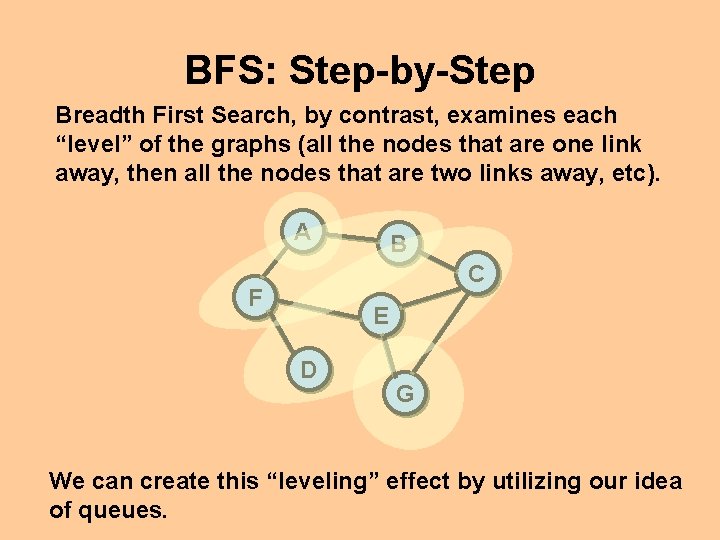
BFS: Step-by-Step Breadth First Search, by contrast, examines each “level” of the graphs (all the nodes that are one link away, then all the nodes that are two links away, etc). A B C F E D G We can create this “leveling” effect by utilizing our idea of queues.

Breadth First Search Given a starting point in the graph G, a history of places we’ve visited, a queue of places we need to go to, and a target value: 1) If the current node is what we’re looking for, return success 2) If we have no places left on our queue of places to try next, return failure 3) Otherwise, enqueue all the links coming off the current node that we haven’t encountered, place the current node on our history and visit the next item off our queue.

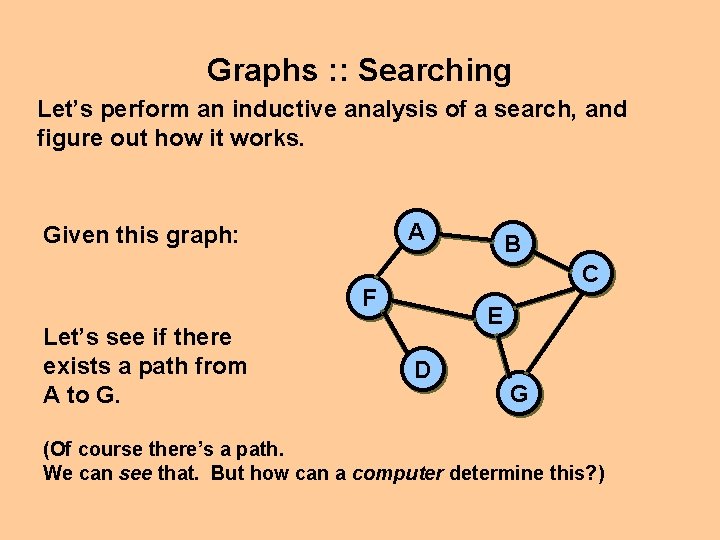
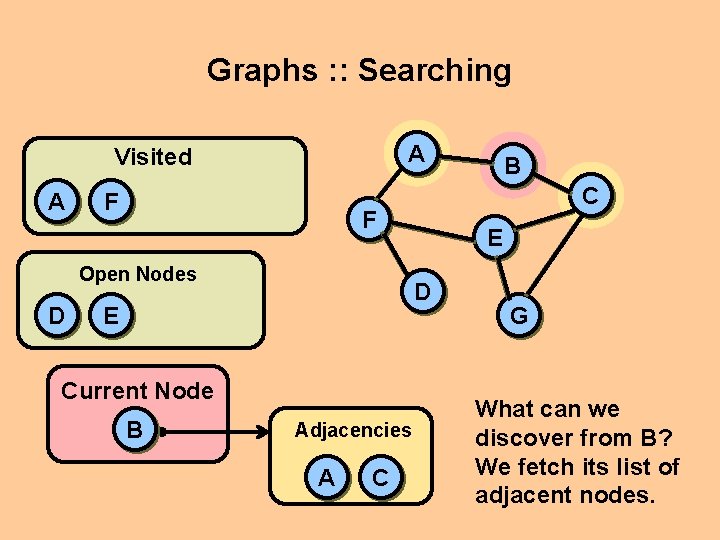
Graphs : : Searching Let’s perform an inductive analysis of a search, and figure out how it works. A Given this graph: C F Let’s see if there exists a path from A to G. B E D G (Of course there’s a path. We can see that. But how can a computer determine this? )

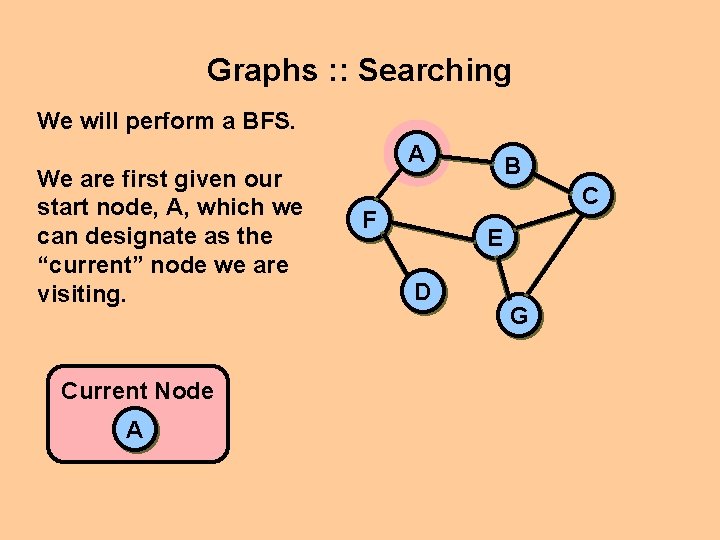
Graphs : : Searching We will perform a BFS. We are first given our start node, A, which we can designate as the “current” node we are visiting. Current Node A A B C F E D G

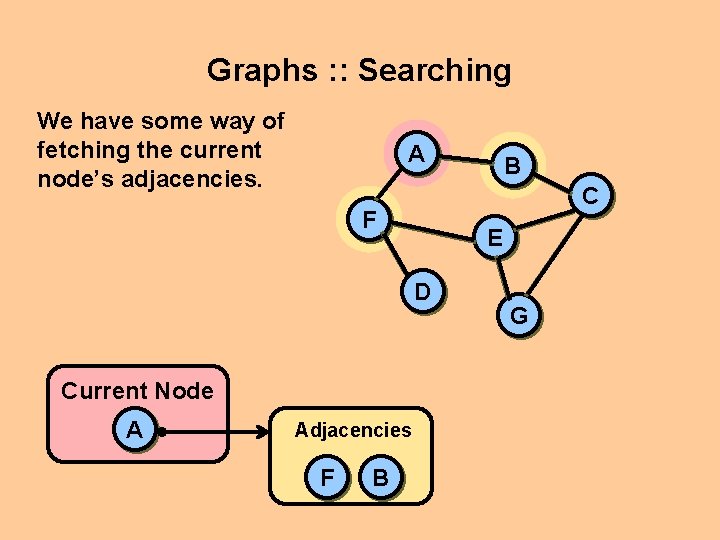
Graphs : : Searching We have some way of fetching the current node’s adjacencies. A C F E D Current Node A Adjacencies F B B G

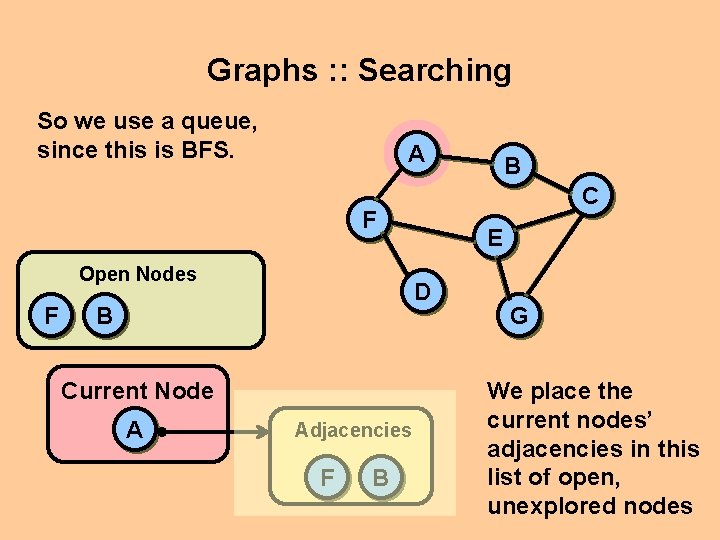
Graphs : : Searching So we use a queue, since this is BFS. A C F Open Nodes F Current Node A E D B Adjacencies F B B G We place the current nodes’ adjacencies in this list of open, unexplored nodes

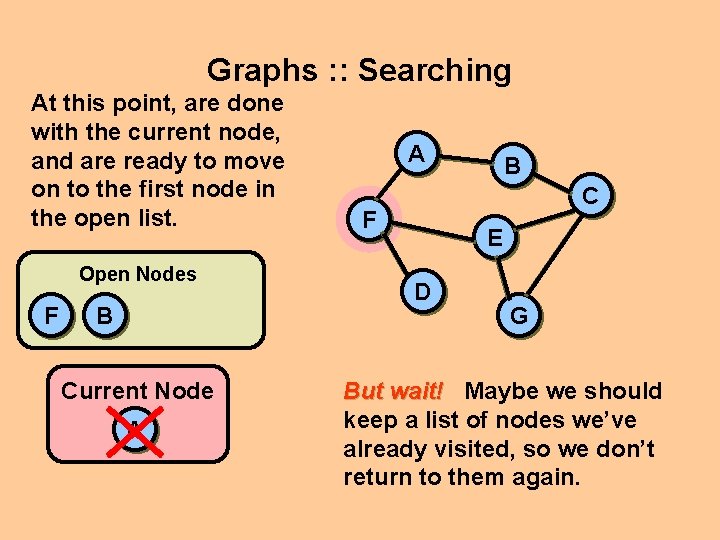
Graphs : : Searching At this point, are done with the current node, and are ready to move on to the first node in the open list. Open Nodes F B Current Node A A B C F E D G But wait! Maybe we should keep a list of nodes we’ve already visited, so we don’t return to them again.

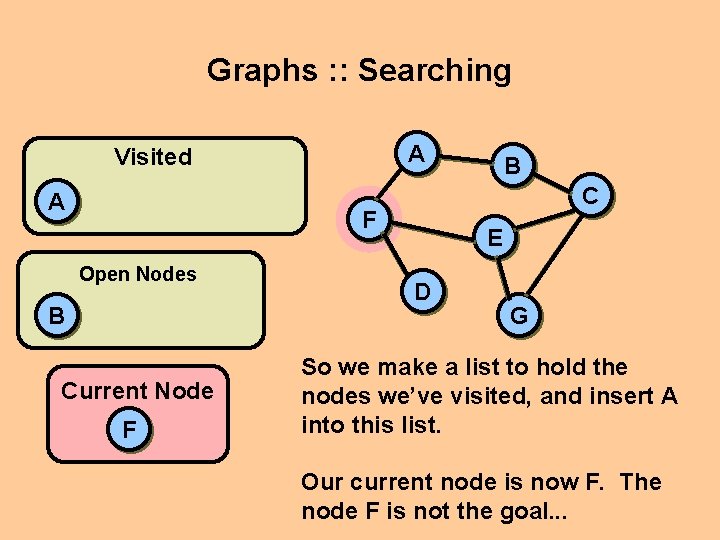
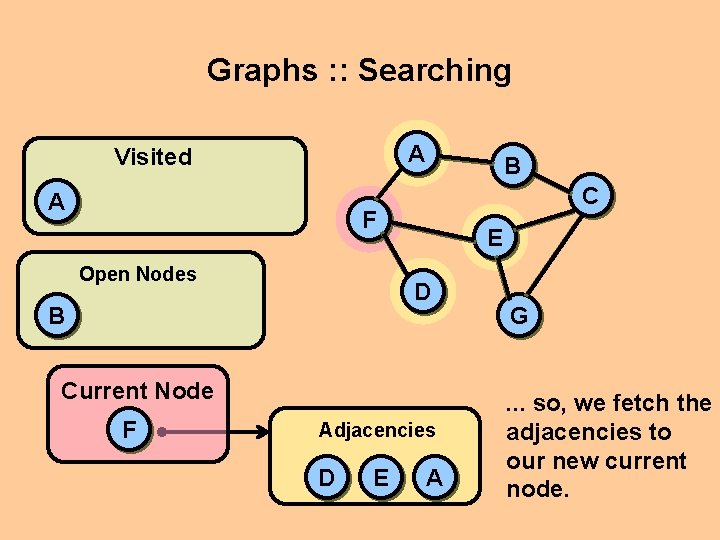
Graphs : : Searching A Visited A C F Open Nodes B Current Node F B E D G So we make a list to hold the nodes we’ve visited, and insert A into this list. Our current node is now F. The node F is not the goal. . .

Graphs : : Searching A Visited A B C F Open Nodes E D B Current Node F Adjacencies D E A G . . . so, we fetch the adjacencies to our new current node.

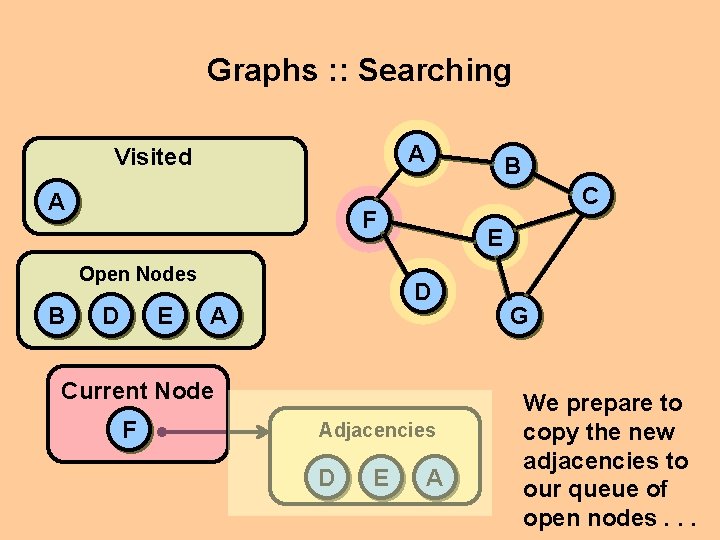
Graphs : : Searching A Visited A C F Open Nodes B B D E E D A Current Node F Adjacencies D E A G We prepare to copy the new adjacencies to our queue of open nodes. . .

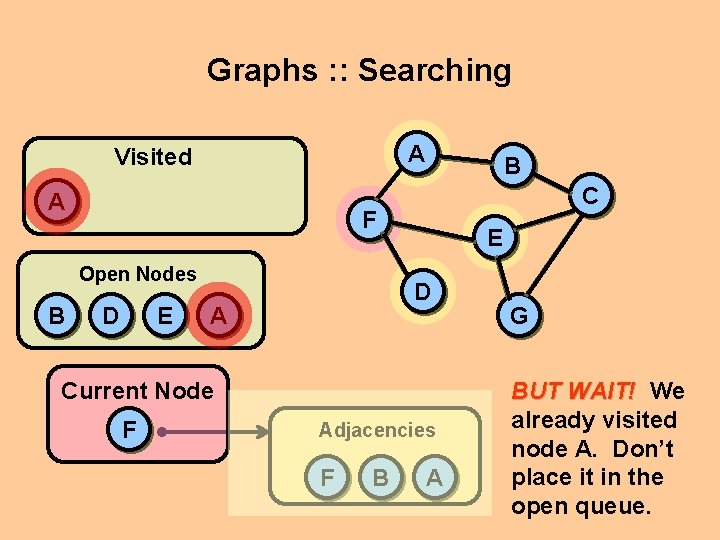
Graphs : : Searching A Visited A C F Open Nodes B B D E E D A Current Node F Adjacencies F B A G BUT WAIT! We already visited node A. Don’t place it in the open queue.

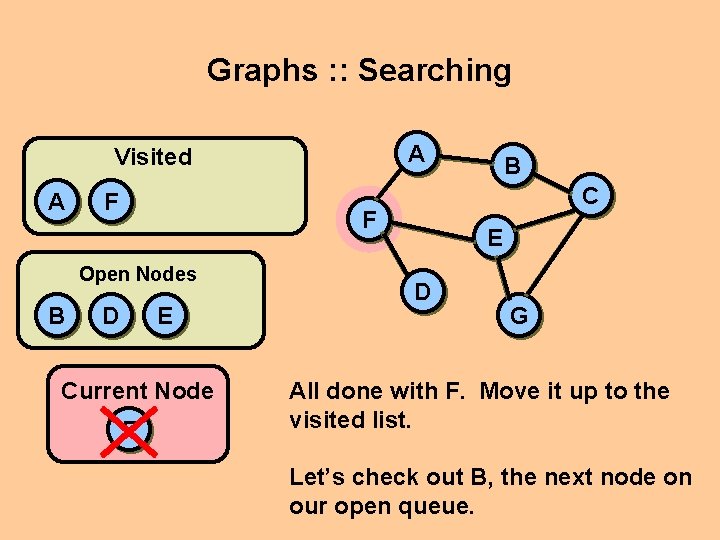
Graphs : : Searching A Visited A F B C F Open Nodes D E Current Node F B E D G All done with F. Move it up to the visited list. Let’s check out B, the next node on our open queue.

Graphs : : Searching A Visited A F D C F Open Nodes Current Node B E D E Adjacencies A C B G What can we discover from B? We fetch its list of adjacent nodes.

Graphs : : Searching A Visited A F D C F Open Nodes E Current Node B E D C Adjacencies A C B G Once again, our list of visited nodes saves us from a cycle in our search

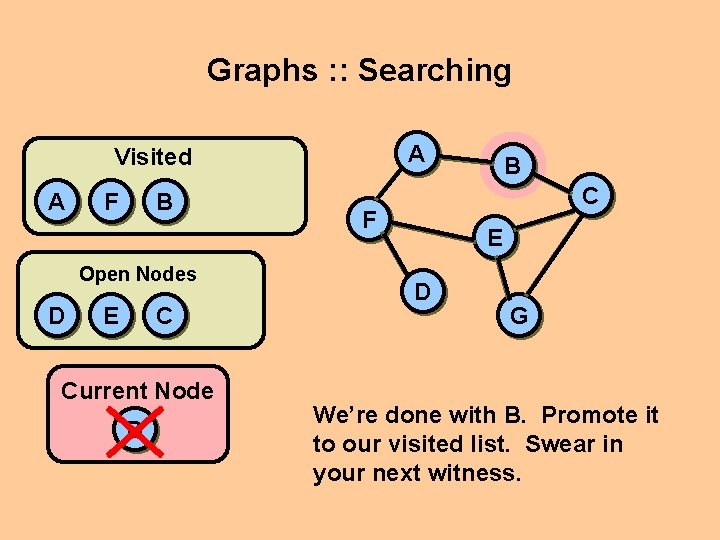
Graphs : : Searching A Visited A F B Open Nodes D E C Current Node B B C F E D G We’re done with B. Promote it to our visited list. Swear in your next witness.

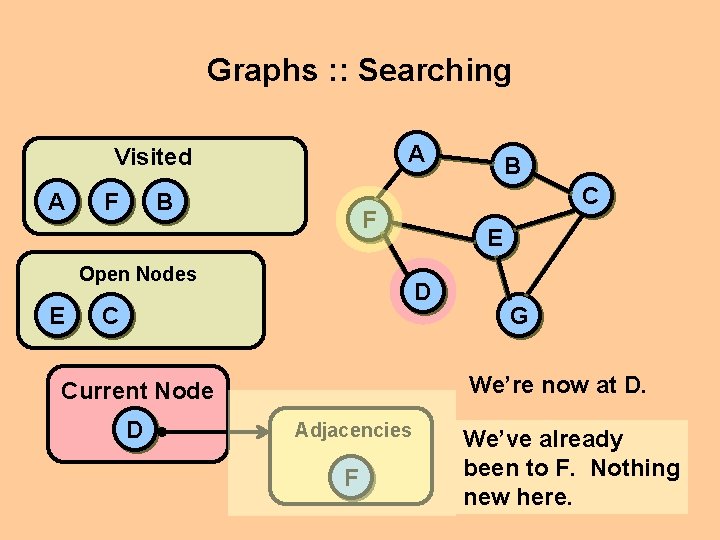
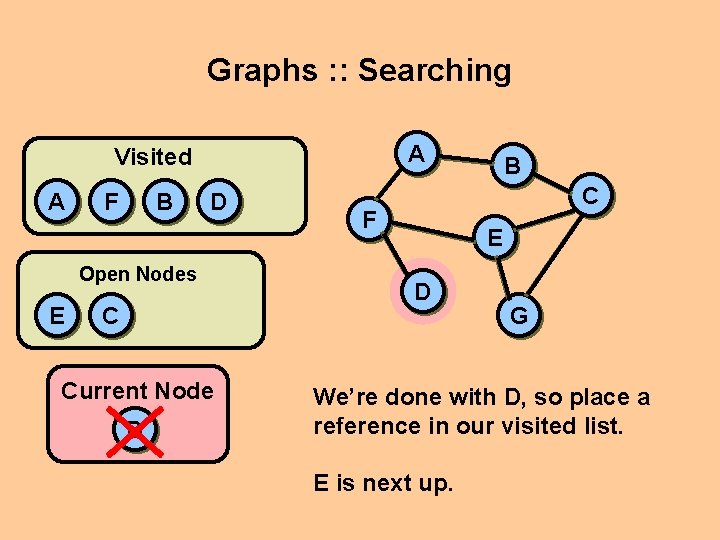
Graphs : : Searching A Visited A F B E E D C G We’re now at D. Current Node D C F Open Nodes B Adjacencies F We’ve already been to F. Nothing new here.

Graphs : : Searching A Visited A F B D Open Nodes E C Current Node D B C F E D G We’re done with D, so place a reference in our visited list. E is next up.

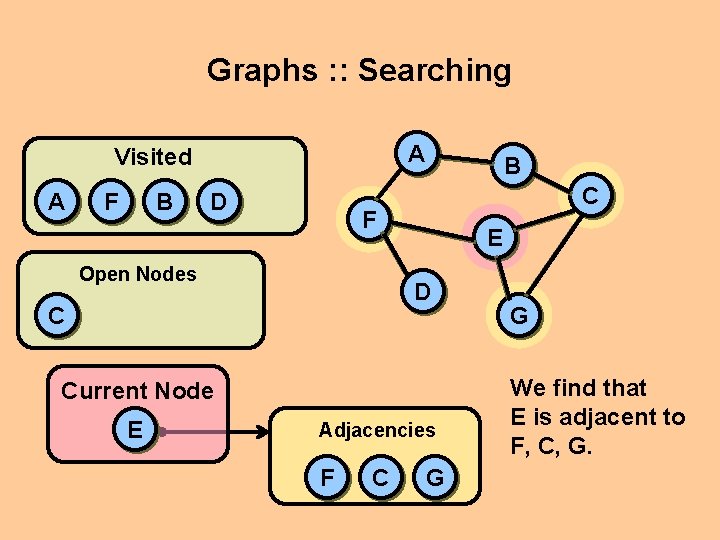
Graphs : : Searching A Visited A F B D B C F Open Nodes E D C Current Node E Adjacencies F C G G We find that E is adjacent to F, C, G.

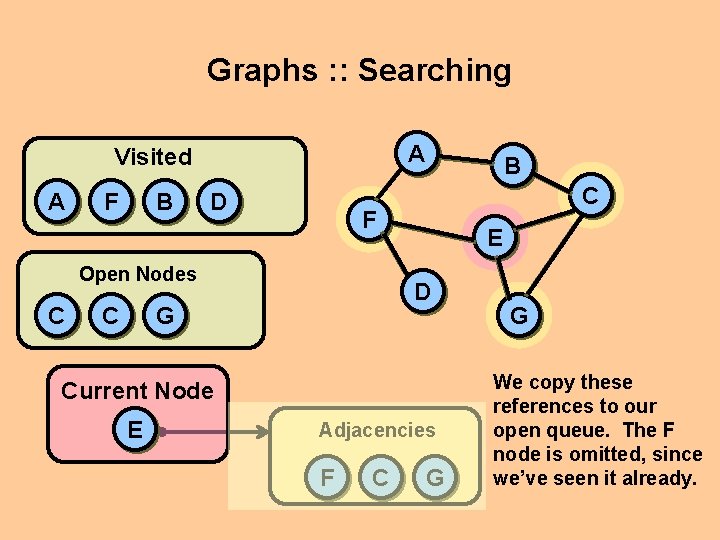
Graphs : : Searching A Visited A F B D C C F Open Nodes C B E D G Current Node E Adjacencies F C G G We copy these references to our open queue. The F node is omitted, since we’ve seen it already.

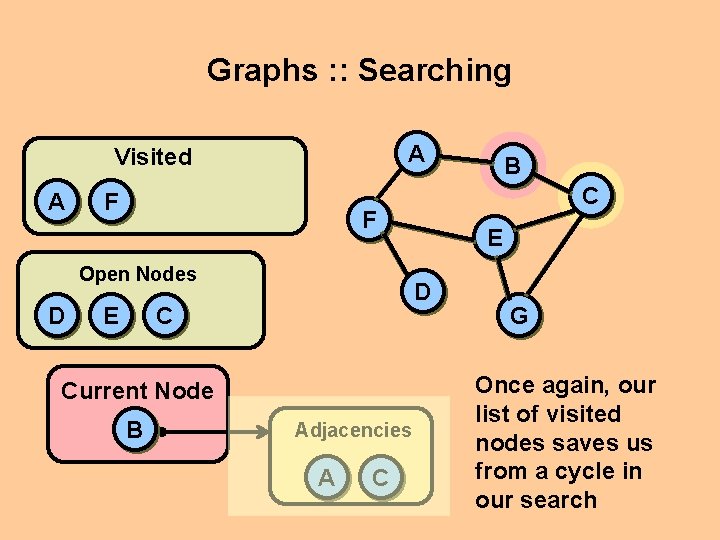
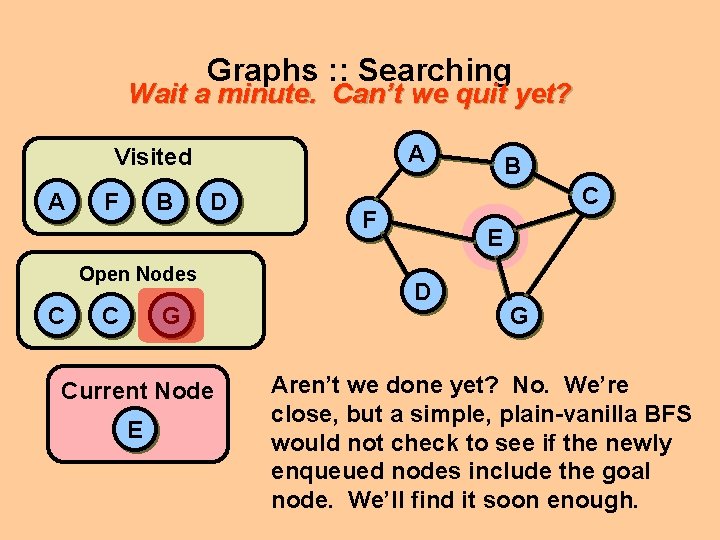
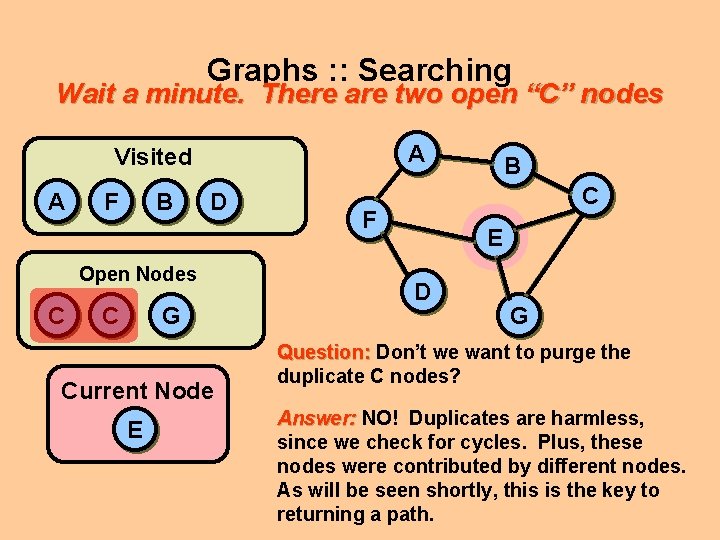
Graphs : : Searching Wait a minute. Can’t we quit yet? A Visited A F B D Open Nodes C C G Current Node E B C F E D G Aren’t we done yet? No. We’re close, but a simple, plain-vanilla BFS would not check to see if the newly enqueued nodes include the goal node. We’ll find it soon enough.

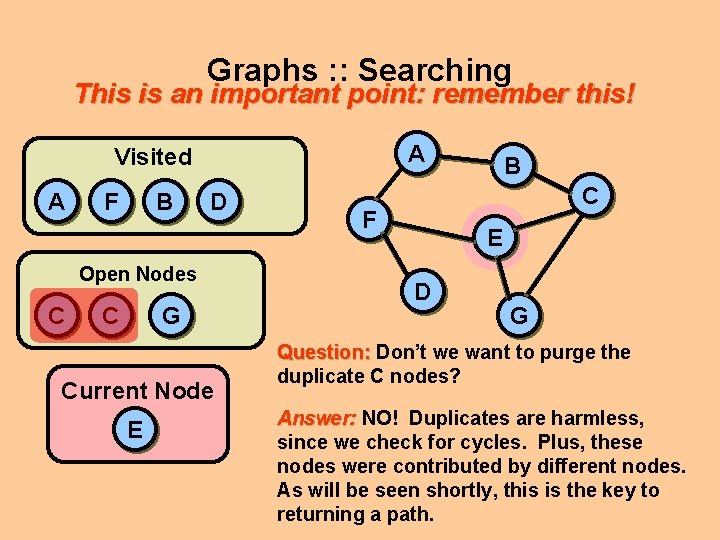
Graphs : : Searching Wait a minute. There are two open “C” nodes A Visited A F B D Open Nodes C C G Current Node E B C F E D G Question: Don’t we want to purge the duplicate C nodes? Answer: NO! Duplicates are harmless, since we check for cycles. Plus, these nodes were contributed by different nodes. As will be seen shortly, this is the key to returning a path.

Graphs : : Searching This is an important point: remember this! A Visited A F B D Open Nodes C C G Current Node E B C F E D G Question: Don’t we want to purge the duplicate C nodes? Answer: NO! Duplicates are harmless, since we check for cycles. Plus, these nodes were contributed by different nodes. As will be seen shortly, this is the key to returning a path.

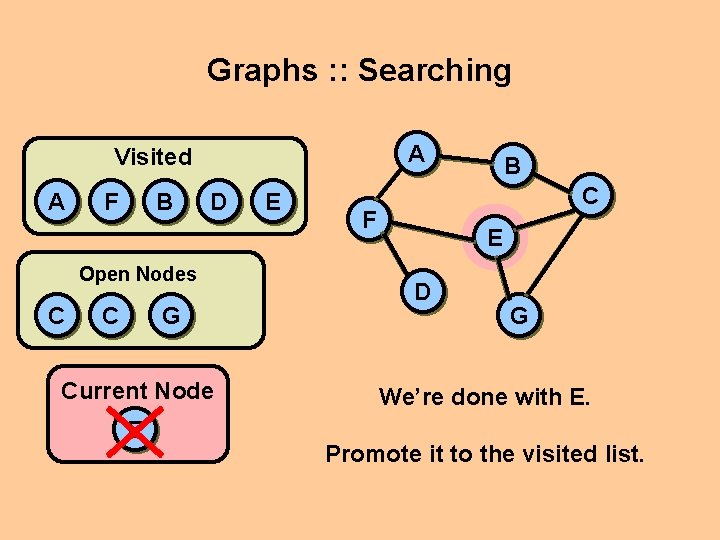
Graphs : : Searching A Visited A F B D Open Nodes C C G Current Node E E B C F E D G We’re done with E. Promote it to the visited list.

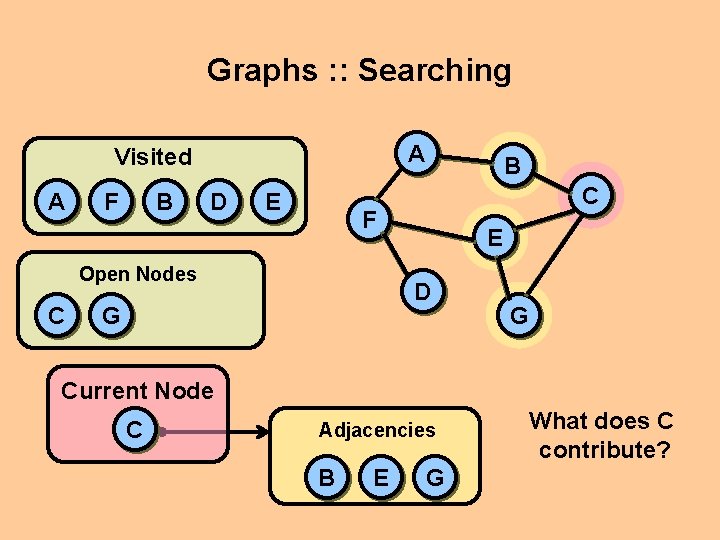
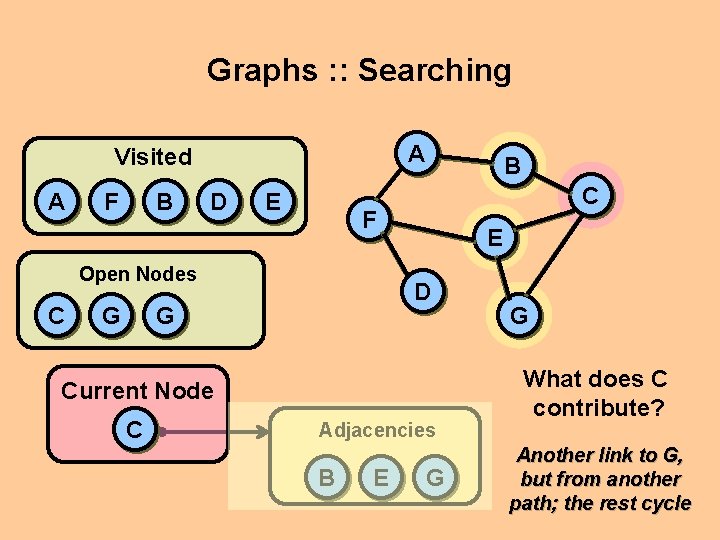
Graphs : : Searching A Visited A F B D E C F Open Nodes C B E D G G Current Node C Adjacencies B E G What does C contribute?

Graphs : : Searching A Visited A F B D E G C F Open Nodes C B E D G Current Node C Adjacencies B E G G What does C contribute? Another link to G, but from another path; the rest cycle

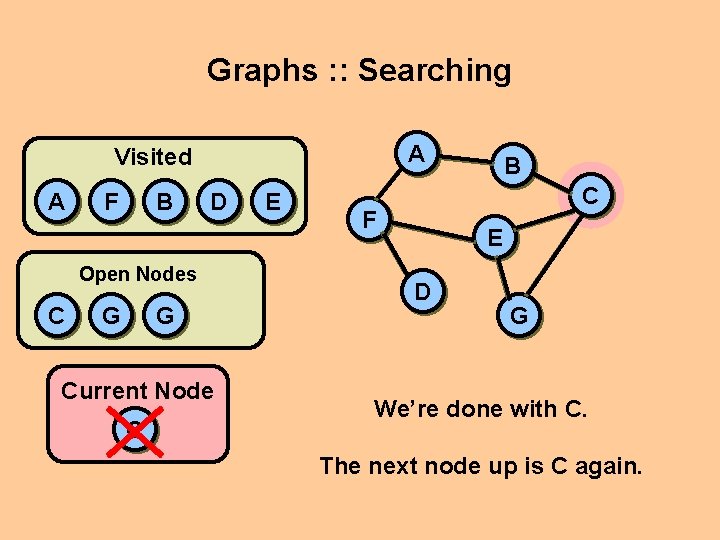
Graphs : : Searching A Visited A F B D Open Nodes C G G Current Node C E B C F E D G We’re done with C. The next node up is C again.

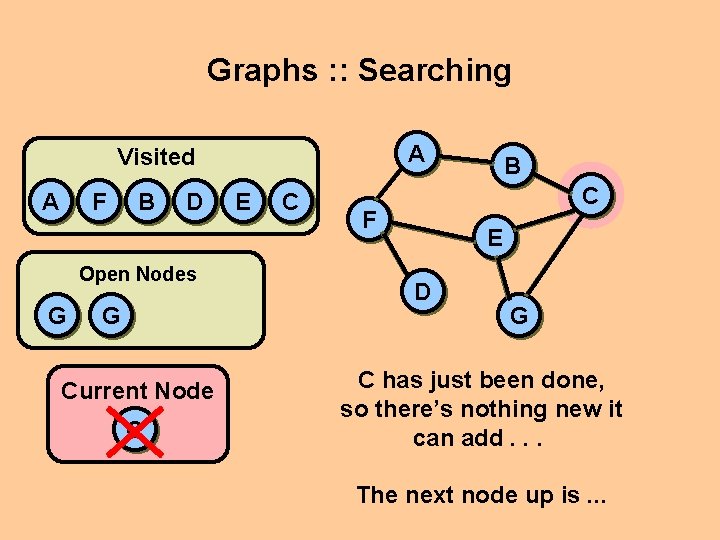
Graphs : : Searching A Visited A F B D Open Nodes G G Current Node C E C B C F E D G C has just been done, so there’s nothing new it can add. . . The next node up is. . .

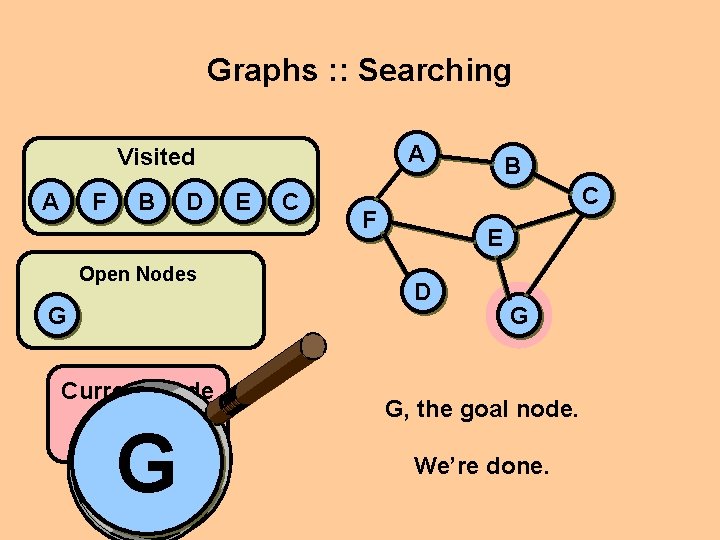
Graphs : : Searching A Visited A F B D Open Nodes G Current Node G G E C B C F E D G G, the goal node. We’re done.

Finding A Path Finding a path in a Graph is another common task that we’ll see over and over again. It’s actually very similar to the searching problems, with the difference that instead of just finding a value in a Graph, we want to represent the series of steps that a person could use to get from one node to another.

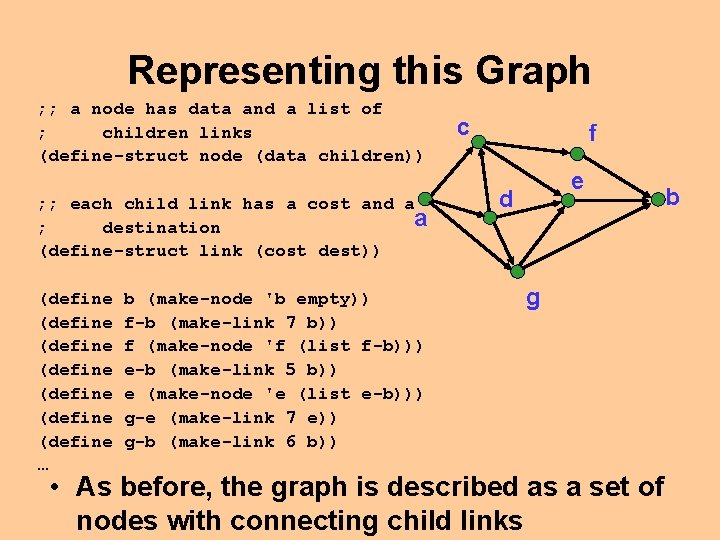
Representing this Graph ; ; a node has data and a list of ; children links (define-struct node (data children)) ; ; each child link has a cost and a a ; destination (define-struct link (cost dest)) (define (define … b (make-node 'b empty)) f-b (make-link 7 b)) f (make-node 'f (list f-b))) e-b (make-link 5 b)) e (make-node 'e (list e-b))) g-e (make-link 7 e)) g-b (make-link 6 b)) c f e d g • As before, the graph is described as a set of nodes with connecting child links b

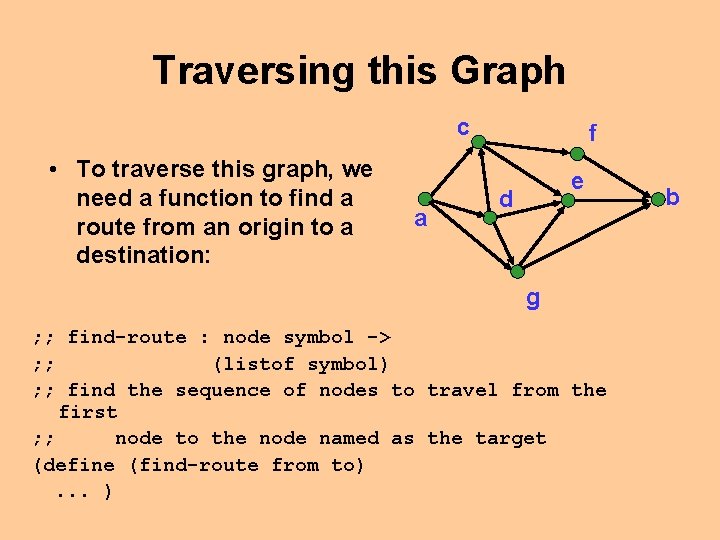
Traversing this Graph c • To traverse this graph, we need a function to find a route from an origin to a destination: a f e d g ; ; find-route : node symbol -> ; ; (listof symbol) ; ; find the sequence of nodes to travel from the first ; ; node to the node named as the target (define (find-route from to). . . ) b

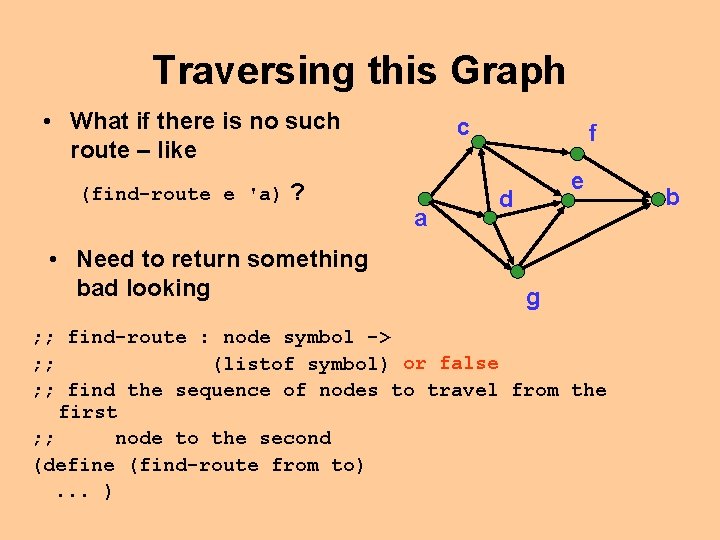
Traversing this Graph • What if there is no such route – like (find-route e 'a) ? • Need to return something bad looking c a f e d g ; ; find-route : node symbol -> ; ; (listof symbol) or false ; ; find the sequence of nodes to travel from the first ; ; node to the second (define (find-route from to). . . ) b

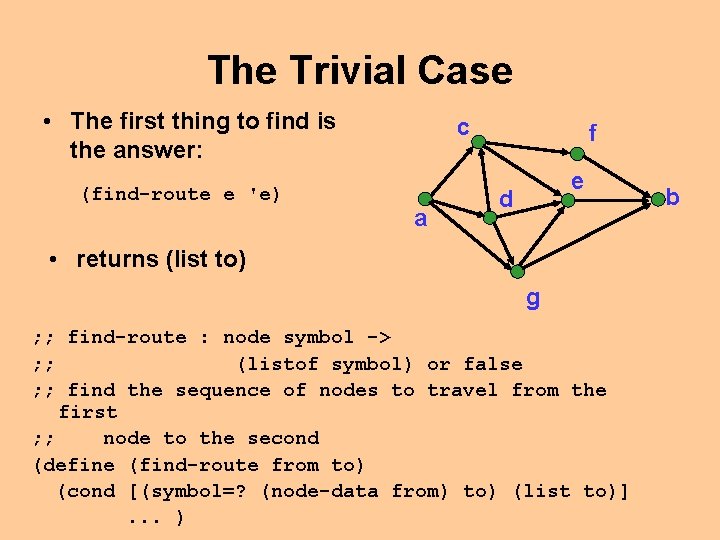
The Trivial Case • The first thing to find is the answer: (find-route e 'e) c a f e d • returns (list to) g ; ; find-route : node symbol -> ; ; (listof symbol) or false ; ; find the sequence of nodes to travel from the first ; ; node to the second (define (find-route from to) (cond [(symbol=? (node-data from) to) (list to)]. . . ) b

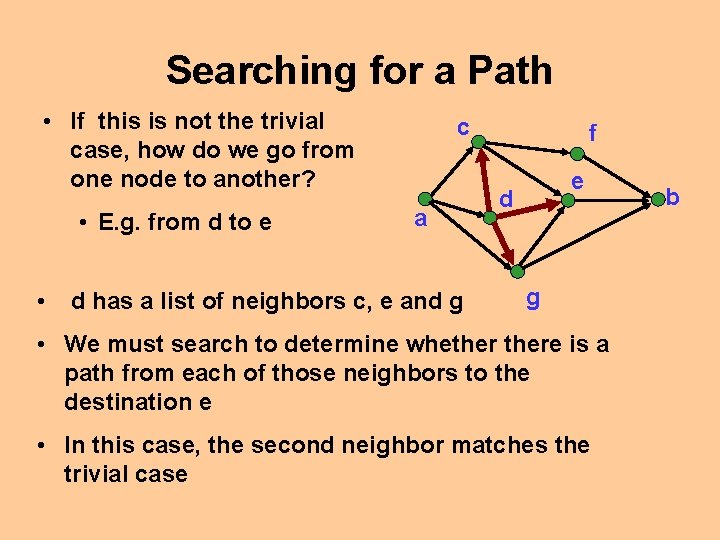
Searching for a Path • If this is not the trivial case, how do we go from one node to another? • E. g. from d to e • c a d has a list of neighbors c, e and g f e d g • We must search to determine whethere is a path from each of those neighbors to the destination e • In this case, the second neighbor matches the trivial case b

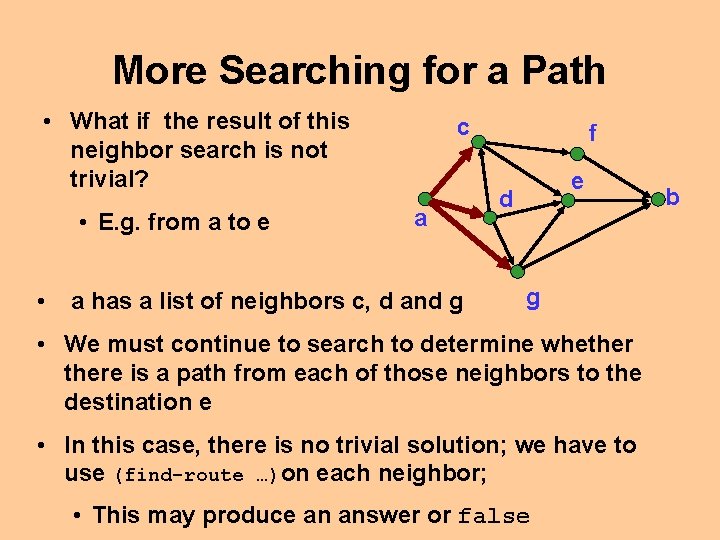
More Searching for a Path • What if the result of this neighbor search is not trivial? • E. g. from a to e • c a a has a list of neighbors c, d and g f e d g • We must continue to search to determine whethere is a path from each of those neighbors to the destination e • In this case, there is no trivial solution; we have to use (find-route …)on each neighbor; • This may produce an answer or false b

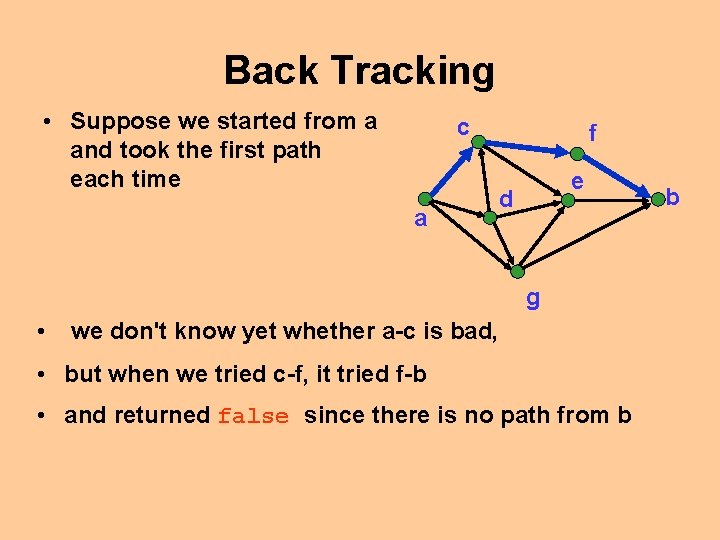
Back Tracking • Suppose we started from a and took the first path each time c a f e d g • we don't know yet whether a-c is bad, • but when we tried c-f, it tried f-b • and returned false since there is no path from b b

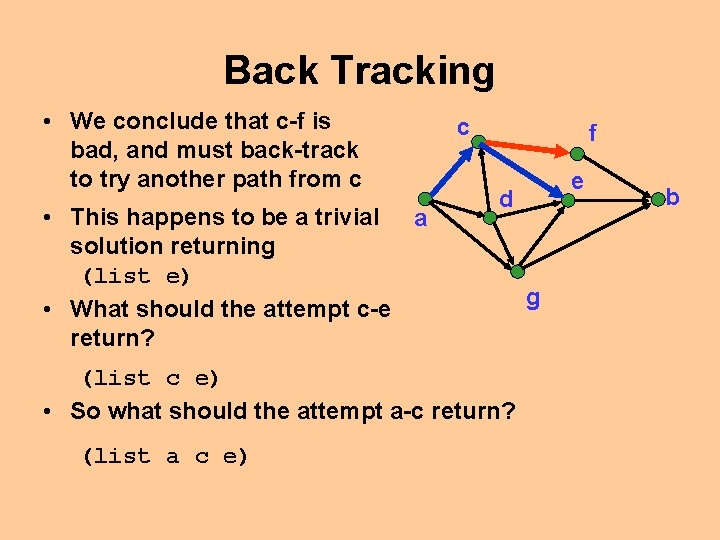
Back Tracking • We conclude that c-f is bad, and must back-track to try another path from c • This happens to be a trivial a solution returning (list e) • What should the attempt c-e return? c f d (list c e) • So what should the attempt a-c return? (list a c e) e g b

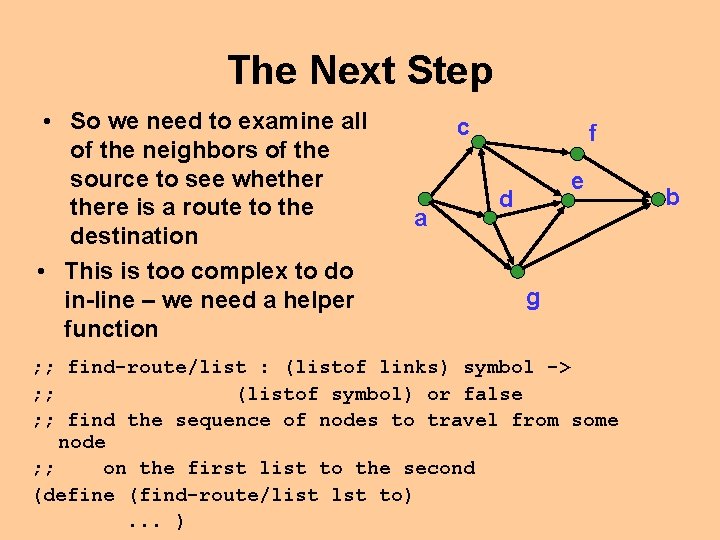
The Next Step • So we need to examine all of the neighbors of the source to see whethere is a route to the destination • This is too complex to do in-line – we need a helper function c a f e d g ; ; find-route/list : (listof links) symbol -> ; ; (listof symbol) or false ; ; find the sequence of nodes to travel from some node ; ; on the first list to the second (define (find-route/list lst to). . . ) b

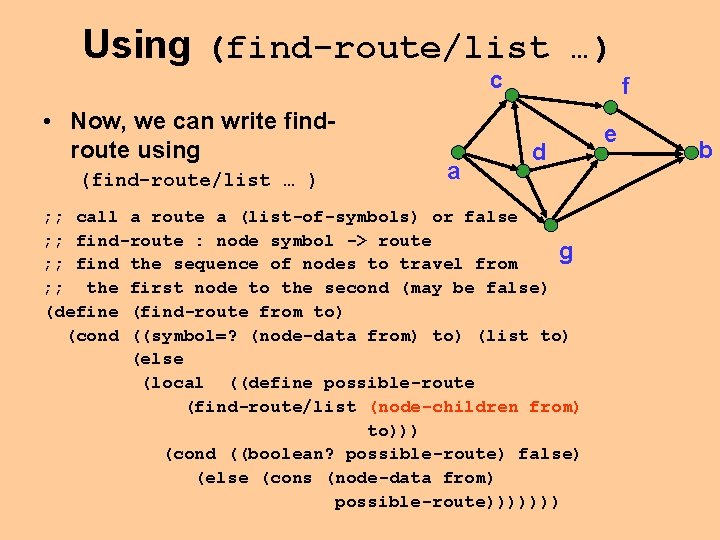
Using (find-route/list …) c • Now, we can write findroute using (find-route/list … ) a f d ; ; call a route a (list-of-symbols) or false ; ; find-route : node symbol -> route g ; ; find the sequence of nodes to travel from ; ; the first node to the second (may be false) (define (find-route from to) (cond ((symbol=? (node-data from) to) (list to) (else (local ((define possible-route (find-route/list (node-children from) to))) (cond ((boolean? possible-route) false) (else (cons (node-data from) possible-route))))))) e b

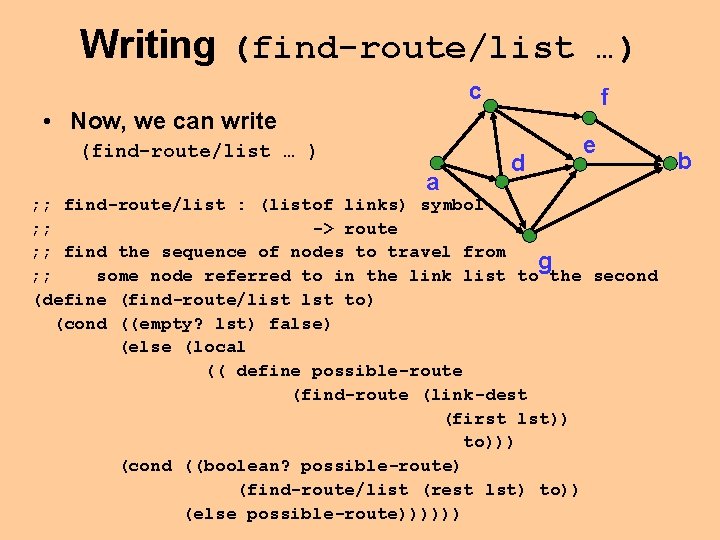
Writing (find-route/list …) c f • Now, we can write (find-route/list … ) a d e ; ; find-route/list : (listof links) symbol ; ; -> route ; ; find the sequence of nodes to travel from g ; ; some node referred to in the link list to the second (define (find-route/list lst to) (cond ((empty? lst) false) (else (local (( define possible-route (find-route (link-dest (first lst)) to))) (cond ((boolean? possible-route) (find-route/list (rest lst) to)) (else possible-route)))))) b

Optimization Algorithms Many real-world problems involve maximizing or minimizing a value: – How can a car manufacturer get the most parts out of a piece of sheet metal? – How can a moving company fit the most furniture into a truck of a certain size? – How can a university schedule its classes to make the best use of classrooms without conflicts?

Optimal vs. Approximate Solutions Often, we can make a choice: – Do we want the guaranteed optimal solution to the problem, even though it might take a lot of work/time to find? – Do we want to spend less time/work and find an approximate solution (near optimal)?

Approximate Solutions

Greedy Algorithms – Approximates optimal solution – May or may not find optimal solution – Provides “quick and dirty” estimates – A greedy algorithm makes a series of “short-sighted” decisions and does not “look ahead” – Spends less time

A Greedy Algorithm Consider the weight and value of some foreign coins: foo bar baz qux $6. 00 $4. 00 $3. 00 $0. 50 500 grams 450 grams 410 grams 300 grams If we can only fit 860 grams in our pockets. . . A greedy algorithm would choose: 1 foo 500 grams = $6. 00 Total of $6. 50 1 qux 300 grams = $0. 50 Optimal solution is: 1 bar 450 grams = $4. 00 1 baz 410 grams = $3. 00 Total of $7. 00

Is a Greedy Algorithm bad?

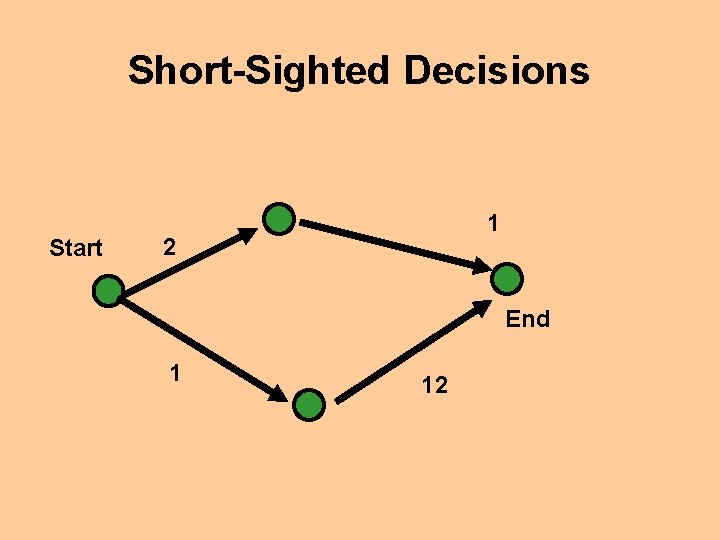
Short-Sighted Decisions Start 1 2 End 1 12

The Shortest Path Problem Given a directed, acyclic, weighted graph… Start at some vertex a What is the shortest path from start vertex say a to some end vertex say b?

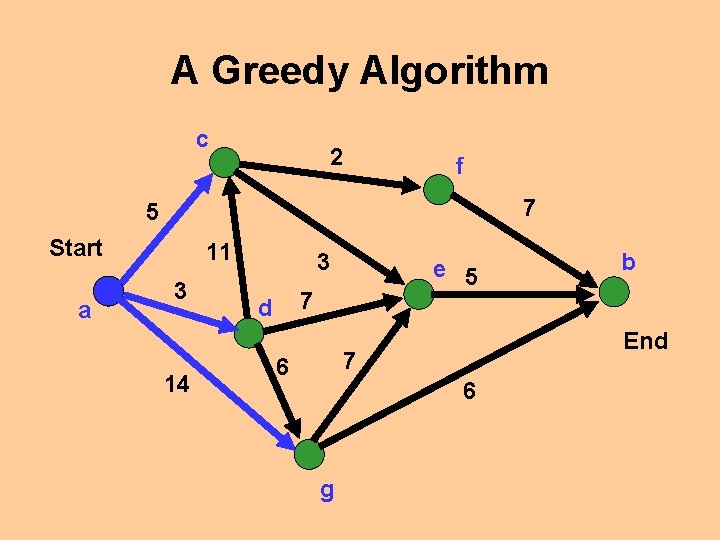
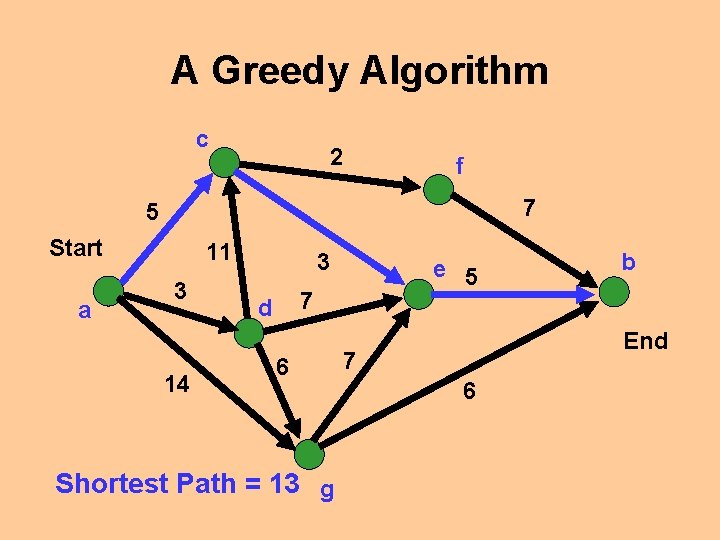
A Greedy Algorithm c 2 f 7 5 Start a 11 3 14 3 e 5 7 d End 7 6 6 g b

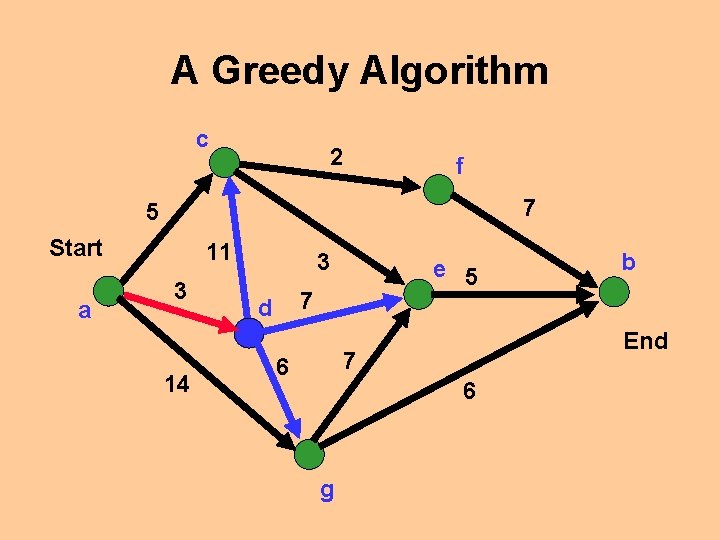
A Greedy Algorithm c 2 f 7 5 Start a 11 3 14 3 e 5 7 d End 7 6 6 g b

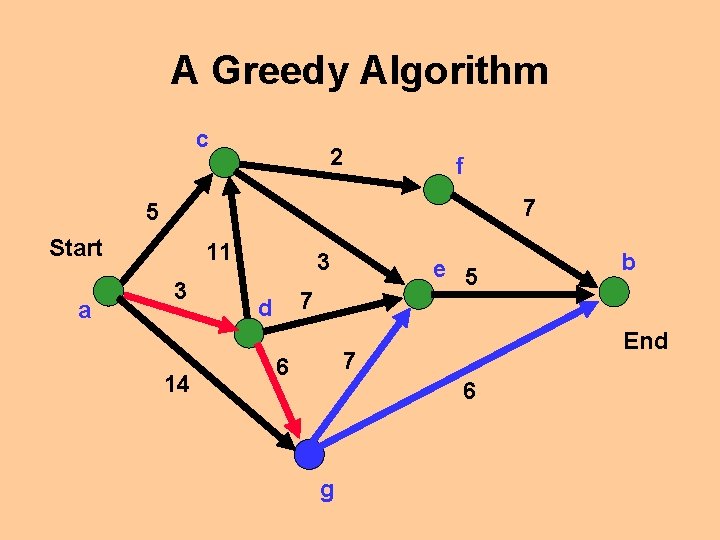
A Greedy Algorithm c 2 f 7 5 Start a 11 3 14 3 e 5 7 d End 7 6 6 g b

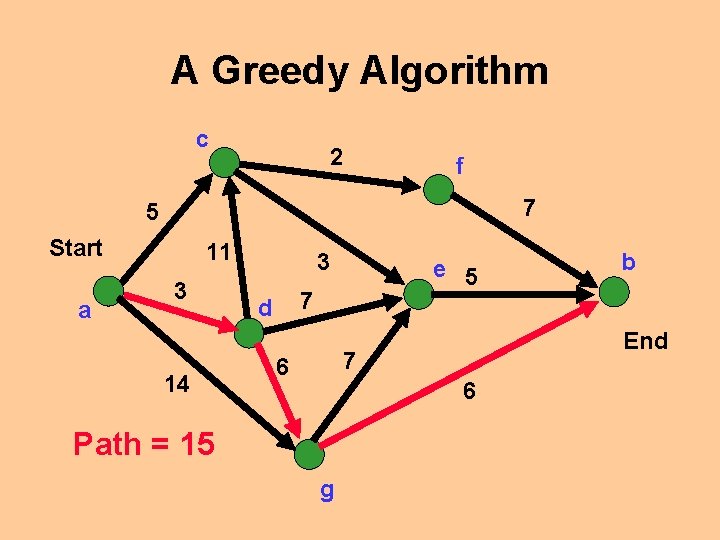
A Greedy Algorithm c 2 f 7 5 Start a 11 3 14 3 e 5 7 d End 7 6 6 Path = 15 g b

A Greedy Algorithm c 2 f 7 5 Start a 11 3 14 3 e 5 7 d 6 Shortest Path = 13 g b End 7 6

Greedy Algorithm Design Generative recursion – Should arrive eventually at the answer – Steps for reaching the answer are indirect ; ; greedy : : node name -> list of links ; ; given a current node and the name of ; ; the target, find the list of nodes to ; ; take you there Note: the solution makes use of Tail Recursion

Code Used 1 ; ; greedy : : node name -> list of links ; ; given a current node and the name of ; ; the target, find the list of links to ; ; take you there (define (greedy from target) (cond ((symbol=? (node-data from) target) (list target)) (else (local ((define this-link (best-link from))) (cond ((not this-link) empty) (else (cons (node-data from) (greedy (link-dest this-link) target))))))

Code Used 2 ; ; best-link : : node -> link ; ; given a node, find the least cost link to somewhere ; ; else (define (best-link from) (best-link-r (node-children from) 100000 false)) ; ; best-link-r : : list-of-links current -> link ; ; given a list and a current cost, find the best link (define (best-link-r lst cost current) (cond [(empty? lst) current] [(< (link-cost (first lst)) cost) (best-link-r (rest lst) (link-cost (first lst))] [else (best-link-r (rest lst) cost current)]))

Code Used 2 ; ; best-link : : node -> link ; ; given a node, find the least cost link to somewhere else (define (best-link from) (best-link-r (node-children from) 100000 false)) ; ; best-link-r : : list-of-links current -> link ; ; given a list and a current cost, find the best link (define (best-link-r lst cost current) (cond [(empty? lst) current] [(< (link-cost (first lst)) cost) (best-link-r (rest lst) (link-cost (first lst))] [else (best-link-r (rest lst) cost current)]))

Code Used 3 (define b (make-node 'b empty)) (define (define (define (define (define f-b (make-link 7 b)) f (make-node 'f (list e-b (make-link 5 b)) e (make-node 'e (list g-e (make-link 7 e)) g-b (make-link 6 b)) g (make-node 'g (list c-e (make-link 3 e)) c-f (make-link 2 f)) c (make-node 'c (list d-c (make-link 11 c)) d-e (make-link 7 e)) d-g (make-link 6 g)) d (make-node 'd (list a-c (make-link 5 c)) a-d (make-link 3 d)) a-g (make-link 14 g)) a (make-node 'a (list f-b))) e-b))) g-e g-b))) c-e c-f))) d-c d-e d-g))) a-c a-d a-g)))