CS 1321 CS 1321 Introduction to Programming Georgia























































































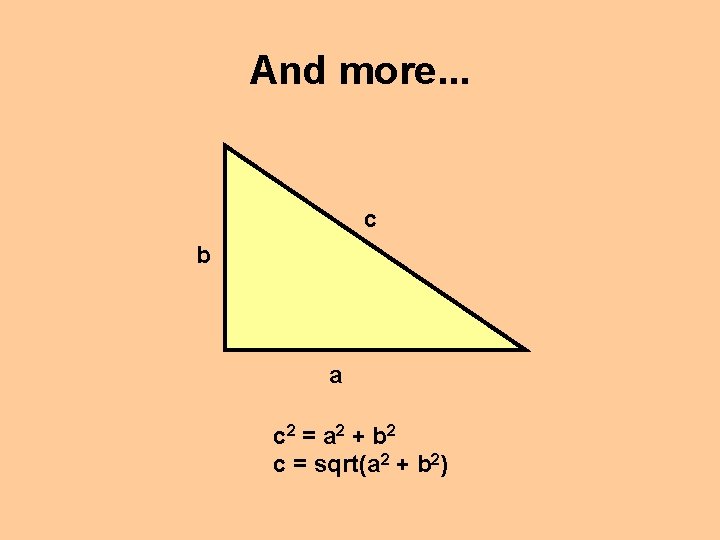
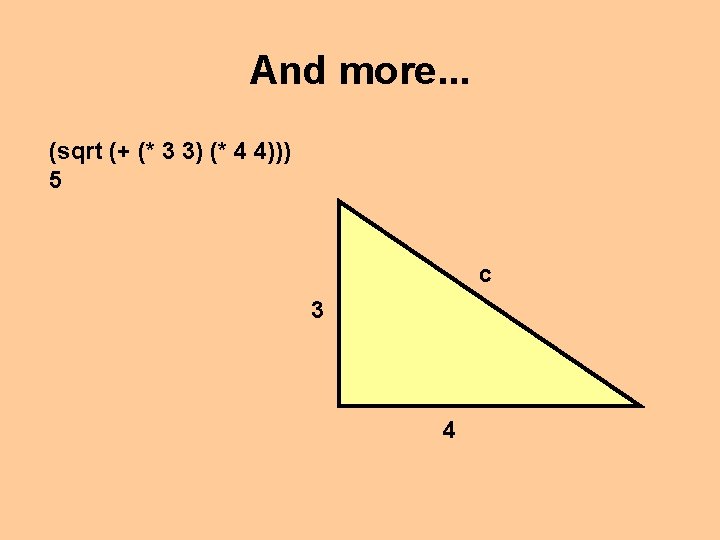








- Slides: 115

CS 1321

CS 1321: Introduction to Programming Georgia Institute of Technology College of Computing Lecture 1 Aug. 21, 2001 Fall Semester

Who I am Who: Monica Sweat Email: sweat@cc. gatech. edu (use cs 1321 in the subject line) (avoid sending me html-formatted email!) Office: Room 120, College of Computing. Course: http: //www. cc. gatech. edu/classes/AY 2002/cs 1321 My website: http: //www. cc. gatech. edu/~sweat Office hours: TBA

University Vocabulary • Lecture: Typically led by Professor or Lecturer. Sometimes big. • Lab: Formerly held in equipped laboratory. Now hands on labs are done on your own. • Recitation: Typically led by Teaching Assistant (TA). Smaller group. Questions and answers.

Basic Schedule Lecture: Tues & Thurs (~1. 5 hours each) You MUST go to the section you’ve signed up for; For example, the homeworks might vary from section to section. Recitation: One night/week 6: 00 p. m. to 8: 00 p. m.

Resources • Book & Dr. Scheme Website – How To Design Programs • Felleisen, Findler, Flatt, Krishnamurthi • http: //www. htdp. org • Class Web Site – http: //www. cc. gatech. edu/AY 2002/CS 1321 – Lecture slides – Examples – On-line Lab Manual – And much more

Resources • Newsgroups – required reading! • My Web Site – http: //www. cc. gatech. edu/~sweat • Lecture slides • Examples • And much more • Again, Dr. Scheme Web Site http: //www. htdp. org

Course Text How to Design Programs Matthias Felleisen Robert Bruce Findler Matthew Flatt Shriram Krishnamurthi ISBN 0 -262 -06218 -6 Online copy available at: http: //www. htdp. org

Help • Follow the following sequence of people – TA (or newsgroup) – Senior TA (STA) – your TA's supervisor – Instructor/Program Manager

Graded items • Tests – given during recitation, dates TBA • Final exam – consult OSCAR for estimated date & time, but subject to change! • Homework – many. 2 -day and 5 day turnaround. Basically assigned one lecture, due the next. • “Lab” - Weekly; often simple. Note: Done on your own – the name “lab” is a misnomer and is misleading.

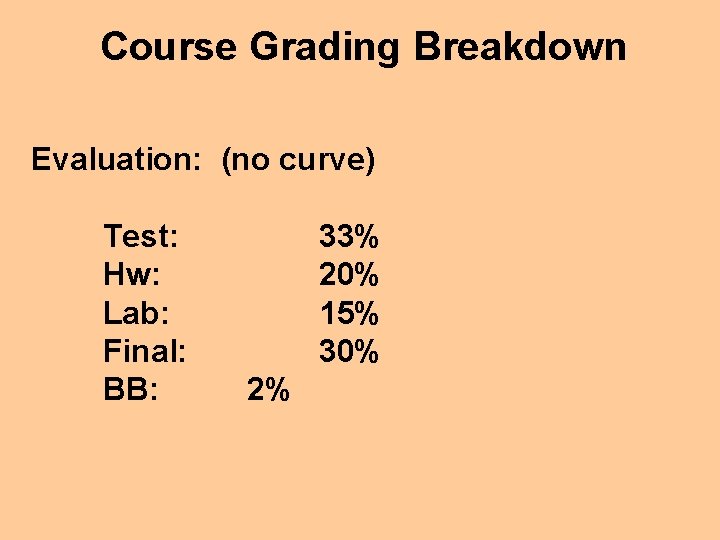
Course Grading Breakdown Evaluation: (no curve) Test: Hw: Lab: Final: BB: 33% 20% 15% 30% 2%

Some Tips For many students this will be your first exposure to Computer Science (unlike Math, Chemistry, etc. )

Tip #1 Don’t wait until the last minute to get help

Tip #2 Hey, can I still pass if I can get enough partial credit? Bad things happen while learning a new skill. You will probably crash and burn on some programs. Start early; give yourself time for mistakes.

Tip #3 Don’t be too ambitious with your course load. You CANNOT slack off in this class, even for a few days.

Tip #4 Watch out for the “big picture”. Don’t forget this is a programming course, not a Scheme course. It’s dangerous to hide from the programming part of the course. You may be crushed on the final.

Today’s Menu 0. What is Computer Science? 1. What is an Algorithm? 2. Why Study Computer Science? 3. Which Computer Language? 4. Why Scheme? 5. Course Mechanics 6. On to Scheme

0. What is Computer Science?

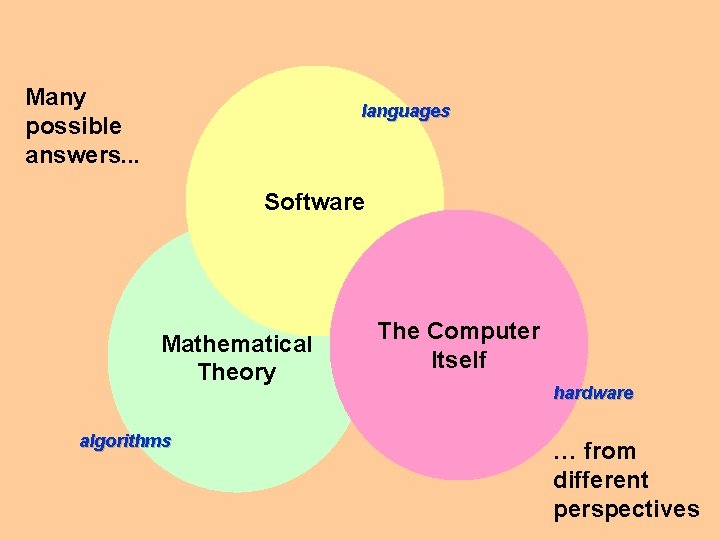
Many possible answers. . . languages Software Mathematical Theory algorithms The Computer Itself hardware … from different perspectives

Definitions “Computer science is the study of what computers do. ”

Rather Dry Definition Computer science, today more accurately a separate discipline, considers a number of rather mathematical topics. In addition to computability questions arising from many problems in discrete mathematics, and logic questions related to recursion theory, one must consider scheduling questions, stochastic models, and so on. Computer Science is no more about computers than astronomy is about telescopes.

Definitions "Computer Science is, simply put, the study of computation. The study of anything that lends itself to a computational model is a study in Computer Science. "

Definitions “Computer science revolves around computational processes, which are also called information processes or simply processes. A process is a dynamic succession of events—a happening. ”

Process—What? ? So we define ‘CS’ based on a study of computational processes--- What’s a process?

A Definition Through Indirection Another way of describing a process is "a procedure in execution. " What's a procedure? A procedure is a collection of instructions, instructions that results in some useful behavior on behalf of the device that executes the instruction. When expressed in a symbolic language, language the procedure is called a computer program.

1. What is an Algorithm?

Algorithms • An algorithm is a precise method of solving a problem • A given problem may be solvable by a number of different algorithms • An algorithm will typically use levels of abstraction to make the solution clearer and implementation easier.

Once upon a time Many years ago programmers realized that programming a complex task would be simpler if they could break the big job down into pieces

Once upon a time This was the birth of modular programming where big programs get broken down into smaller pieces called modules, methods, subroutines, procedures or functions.

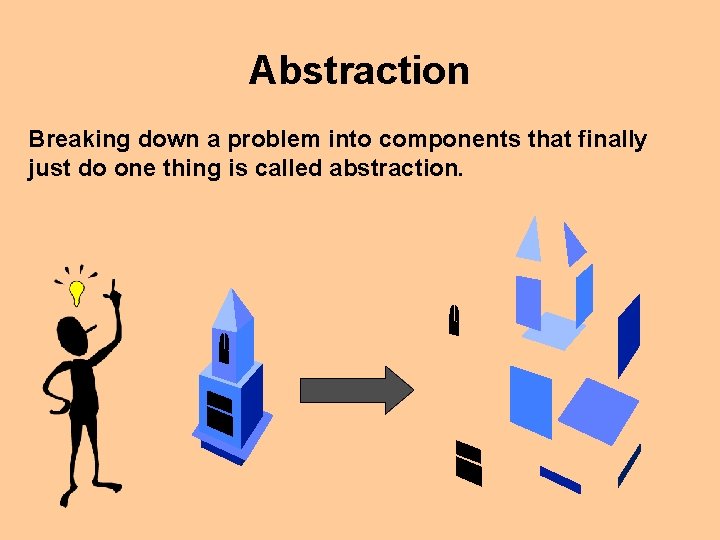
Abstraction Breaking down a problem into components that finally just do one thing is called abstraction.

Algorithms & Abstraction • A key feature of a well written algorithm will be proper use of abstraction • This will provide an algorithm that – – is more understandable is easier to implement and test provides more reusable modules will get a higher grade!

2. Why Study Computer Science?

Myth: Computer science is for techno geeks who want to drive expensive luxury imports. Truth: Computer science should be at the core of a liberal arts education. The essence of computer programming: Describing adequately the process to be used to perform some task is an essential skill in all professions

Imagine Taking a class about bicycling And never getting on a bike! So we propose to you, to spend some cycles learning about computer programming Will you be ready for the Tour de France?

The Inevitable. . . If we propose to study CS, we need the convenience of a symbolic language to express and communicate our instructions. Hence, we’ll use a computer language to learn about processes and procedures.

3. Which Computer Language?

A# ABC ABEL ABCL ACCENT ACTOR ADA ADL AGORA AKL ALEF ALEPH ALF ALGOL AMBER AMIGA E AML AMPL appall AVAIL AWK B BABEL BASIC BAWK Be. BOP BEFUN BETA BEGL BERTRAND BIGWIG BISTRO BLISS BLUE BRIAN BRILLIANT BSL C C++ (GNU CECIL CHARITY CHEETAH CHi. LL CILK CLAIRE CLARITY CLEAN CLIPS CLOS C COBOL COLD FUSION COMAL COMMON LISP COOL COMPONENT PASCAL CORBA COSY CWEB DAD DARK BASIC DELPHI DEMETER DIALECT DRAGOON DYL DYNACE E ECLIPSE Eiffel EGG ELF ELASTIC C ELLIE EMERALD ENIAC ERLANG ES Eu. LISP EUPHORIA FRANZ LISP FMPL FORMS/3 FORTH FORTRAN G GEL GENTLE G G+DEL GREEN GUILE HASKELL HOPE HPCODE HUGO ICI ICON INFER ISWIM J JAD JAVA BEANS JAVASCRIPT Jo. CAML JOY JUICE K KALEIDOSCOPE KEVO LAGOONA LAURE LEDA LENS LIANA LIFE LIMBO LINDA LISP LML LOGO LOOEE LOOKS LO LUA LUSTRE M 4 MAGENTA MAGMA MATCHMAKER MATLAB MCPL MELD C M MERCURY MEROON MIRANDA MISA ML MODULA 2 MODULA 3 MOPS MOZART MUM NAPIER 88 NAWK NEON NESL NET REXX NEWTON NIAL O 2 OAKLISP OBERON OBJECTIVE CAML OBJECT OBLIQ OCCAM OCTAVE OLABL OMEGA O OPAL ORCA OSCAR OSQL OZ PAL PARASOL PARLOG++ PASCAL PERL PECOS PFL PHOCUS PHANTOM PHP PICO PICT PIKE PILE PIRANHA PIRL PIZZA PL/B PL/I PLAN PLAIN PLIANT POLKA POLYGOTH PRESTO PROGRESS POOL POPTALK POST POWERBUILDER PROBE PROFAN PROGRAPH PROLOG PROMETHEUS PROTEUS P PYTHON Q QUEST R REBOL REFINE REGINA RELFUN REXX RPG RUBY S SAT SCALLOP SCHEME SCREAMER SCRIPT X SED SELF SEQUENCE L SEPIA SIMU SIRI SISAL SMALLTALK SMSL SNAML SNOBOL SNOOPS SPANNER SQUEAK SQL SR SUNEIDO T 3 X Tcl/TK TECO TELESCRIPT TELOS TEMPO THETA TOM TOP TRAITS T TURBO PASCAL TURING TYCOON UFO UNLAMBDA V VIRT VISUAL BASICSCRIPT VISUAL C++ WINDUCTOR WINTERP WOOL XLISP XML YAFL YERK YO Flavors Assembler, C, C++, Fortran, Java, Scheme, Lisp

? What’s the purpose of a computer language?

Consider To understand why there are so many computer languages, we might also consider why there are many spoken languages. Exactly how many spoken languages are there?

Consider: Total Living Languages Percentage The Americas 1, 000 15% Africa 2, 011 30% Europe 225 3% Asia 2, 165 32% The Pacific 1, 302 19% -----TOTAL 6, 703 Why do people speak different languages? What is the purpose of a human language? Source: www. sil. org/ethnologue

Insight We have so many spoken languages because there are so many cultures and contexts for societies. Similarly, there are many different computer languages because they each come from unique contexts, and address different types of problems and needs.

? Asked Another Way Why are there so many computer languages? (Why not create one “perfect” computer language? ) For whom does one write programs in a language? (Why not write them in 1 s and 0 s? )

Typically Different types of problems lead to different approaches with computer languages < < < < Scientific computation - Fortran List processing - Lisp Business programming - Cobol Systems programming - C Old CS education favorite – Pascal Object-Oriented programming – C++ OOP that’s good for running over internet - Java

Computer Languages Computer languages have two related purposes: 1. efficiently provide instructions to machines that execute programs and procedures Computer consumption 2. provide a clear written record of theory or idea expressed in the procedure Human consumption

Computer Languages We could program in 1 s and 0 s (machine language), but will instead employ a high-level language. We’re using a language called Scheme, plus introducing some basic software tools (Matlab, Excel, HTML, etc. ) But note that: -- what you learn is not restricted to the language -- ideas expressed in the language can be expressed in other languages

Revelation We are therefore writing programs in Scheme (and not 1’s and 0’s that the computers prefer) because. . . we want other people to understand our ideas and programs. In other words, computer languages are used to communicate with OTHER PEOPLE (as well as computers).

Note! This is not a class in Scheme programming This is a class about computation and problem solving. It’s just handy to actually use a programming language while we study the subject at hand – programming and problem solving. Scheme is "incidental but essential" to the course subject. We’re more concerned about programming.

4. Why Scheme?

Scheme? The choice of Scheme for beginners is natural. Permits programmers to focus on two key elements of programming: Programs as relations between quantities Evaluating programs for specific inputs. Using just this core language, students can develop complete programs during the first session with a teacher.

Scheme? The choice of Scheme for beginners is natural. Easily arranged as a tower of language levels. As students learn more about programming and the language, the teacher can expose students to richer layers of the language, which allows students to write more interesting and more concise programs.

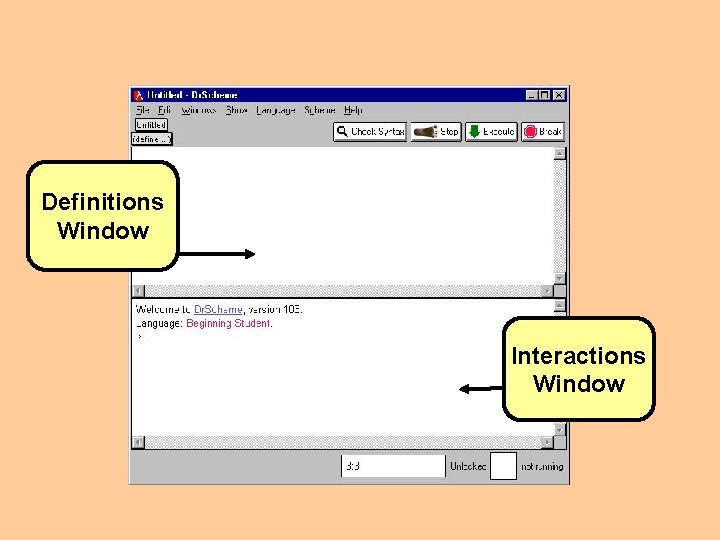
Scheme? The choice of Scheme for beginners is natural. The Dr. Scheme programming environment offers a truly interactive evaluator. Definitions window where students define programs Interactions window which acts like a pocket calculator. You can enter expressions into the interactions window, and Dr. Scheme determines their values (just like with pocket-calculator arithmetic). You proceed from there to calculations with structures, lists, and trees--the kinds of data that computer programs often manipulate.

Scheme? The choice of Scheme for beginners is natural. Use of an interactive evaluator with a rich data language permits you to focus on problem solving and program design activities. An interactive mode of evaluation encourages you to experiment in all kinds of ways and satisfy your curiosity!

Scheme? The choice of Scheme for beginners is natural. The nature of Scheme requires programmers to use good abstraction to solve a problem. Many computer scientists consider learning a functional language like Scheme to be an essential part of learning the process of abstraction.

But we wanted to use a cool real-world language!!!

“Real World” Use of Scheme is used!: -- NASA’s 1999 Software of the Year was a Lisp program controlling the Deep Space 1 spacecraft. -- Powers parts of Yahoo’s backend -- CAD software engines used Lisp -- It’s used by professionally trained software engineers

Why Use Scheme? Core Material at other Universities Berkeley Brown CMU Indiana MIT Rice Utah Yale Florida

Why Use Scheme? Speed -- Rapid prototyping -- Development time (more expensive than execution time) is quicker

Why Use Scheme? Speed (cont’d) -- Scheme (derived from Lisp) has an execution time that well to many other ‘fast’ languages “We have repeated Prechelt's study using Lisp as the implementation language. Our results show that Lisp's performance is comparable to or better than C++ in terms of execution speed, with significantly lower variability which translates into reduced project risk. Furthermore, development time is significantly lower and less variable than either C++ or Java. ” NASA study of Lisp www-aig. jpl. nasa. gov/public/home/gat/lisp-study. html

Why Use Scheme? Cost Free! Money allocated for an expensive C++ compiler can now be squandered elsewhere.

• SCHEME is a statically scoped and properly tail-recursive dialect of the LISP programming language invented by Guy Lewis Steele Jr. and Gerald Jay Sussman. It was designed to have an exceptionally clear and simple semantics and few different ways to form expressions. A wide variety of programming paradigms, including imperative, functional, and message passing style, find convenient expression in SCHEME. • SCHEME has lexical scoping, uniform evaluation rules, and uniform treatment of data types. It does not have the concept of pointers, uninitialized variables, specialized looping constructs, or explicit storage management. In SCHEME all data types are equal. What one can do to one data type, one can do to all data types. There are seven kinds of expressions: constant, variable reference, procedure creation, procedure application, conditional, assignment, and sequence. • Numbers are especially interesting in that an integer is a rational and a real is a complex. SCHEME requires no looping constructs. Any function which calls itself in the "Tail" position is just a loop. • SCHEME has several important advantages: it's elegantly simple in that regular structure and trivial syntax avoids "special case" confusion. It's expressiveness means that one spends little time trying to work around the language, it concentrates on what they want say rather than on how to say it. It supports a variety of styles (including OO); allows users to better match their solution style to the style of the problems to be solved. There’s Much, Much More. . .

Scheme is cool

Finally What do you call someone who speaks three languages? What do you call someone who speaks two languages? What do you call someone who speaks one language?

Ga Tech Experience Monolingual programmers are not well equipped for the real world

Tough Nut to Crack a v Ja Sch e me CS COMPUTATION C + + C

6. On to Scheme )

Installing Dr. Scheme http: //www. htdp. org

In cs 1321, you will use the Dr. Scheme program as your editor and development environment

Definitions Window Interactions Window

Execute buttons loads the Definitions into the Interactions window

Saving your work

Important Be sure to set the language level in Dr. Scheme to “Beginning Scheme”, then click on "Execute”

Perspective We might categorize computer languages: procedural or imperative languages -- BASIC, FORTRAN, C, Pascal -- Reflect low-level focus of language -- Programmers must create solutions that reflect the type of hardware, restrictions and limits of the system they are using

Perspective Object-oriented programming -- Java, C++, Ada, Smalltalk -- Programmers must think in terms of data and the behaviors appropriate to that data -- Less design pressure from the limits and requirements of the computer system.

Perspective Functional Programming -- Lisp, Scheme -- Programs viewed as a collection of procedures similar to mathematical functions. -- Much easier to implement

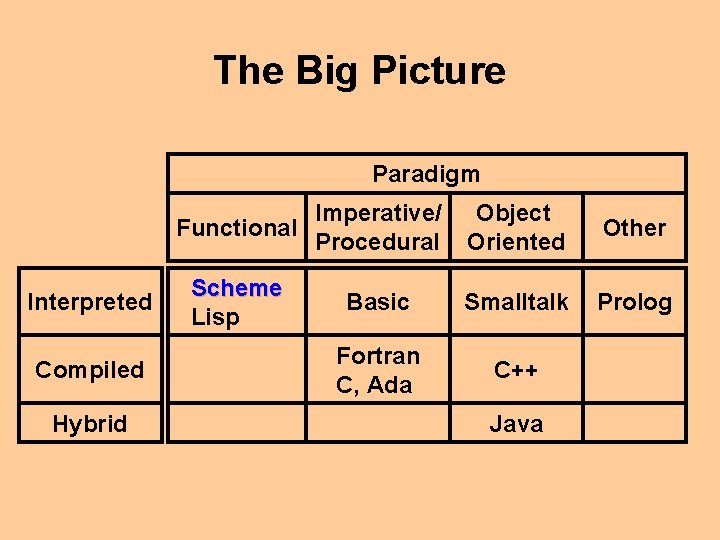
Further Perspective In addition to labels of functional, procedural, and OO languages, we might also categorize languages based on whether they are interpreted or compiled (or even a hybrid). Interpreted languages are evaluated one step at a time, with values and variables being determined dynamically at run time. Compiled languages are assembled into memory, with address locations and offsets precalculated, and then crafted into an “executable” program.

The Big Picture Paradigm Interpreted Compiled Hybrid Functional Imperative/ Procedural Object Oriented Other Scheme Lisp Basic Smalltalk Prolog Fortran C, Ada C++ Java

So • Scheme can execute a single line of code as soon as it is typed into the interactions window (+ 2 2) 4

Simple Evaluation Let’s start with something simple. Suppose we wanted to solve the following expression: 3 + 4 * 5 This looks easy, but what might go wrong?

Simple Evaluation It might be that by mistake someone could read this as “ 7 * 5” by adding before multiplying. A clear mistake. 3 + 4 * 5 How can we be sure nobody makes this mistake?

Simple Evaluation We can add unnecessary but helpful parentheses around part of the expression. 3 + (4 * 5) We all know that parenthetical expressions are evaluated first… So this will make it totally clear.

Simple Evaluation We can go further, and add parentheses around the entire expression. (3 + (4 * 5)) This doesn’t change the meaning of our original short notation. It makes things explicit.

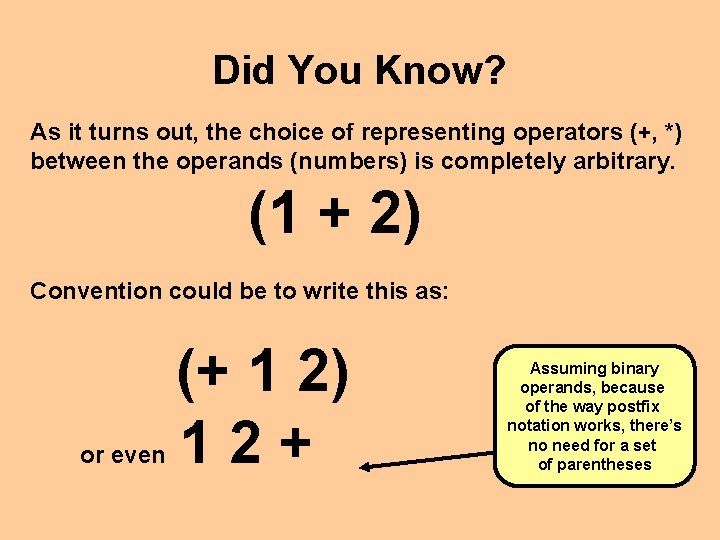
Did You Know? As it turns out, the choice of representing operators (+, *) between the operands (numbers) is completely arbitrary. (1 + 2) Convention could be to write this as: or even (+ 1 2) 12+ Assuming binary operands, because of the way postfix notation works, there’s no need for a set of parentheses

Prefix Notation Scheme uses prefix notation, where the operation call occurs first, followed by the data or arguments. ( <operation> <data> ) Examples: (+ 2 2) (* 3 1) (/ 10 0) (* 7 (+ 4 5)) Which of these would cause problems if entered into a simple calculator?

Prefix Notation Self quiz: Write the following expression in prefix notation: 1) subtract 3 from 5 2) subtract 10 from the quantity 5 minus 8 3) divide 3 into 42 4) sum the squares of both 3 and 4

Using Dr. Scheme (in class demonstration)

Using the Stepper Dr. Scheme includes a remarkable stepping tool that let’s you see the order of evaluation. Let’s evaluate some complex expressions with this tool. (/ (* 2 4) (/ (* 6 4) (* 12 4))) (in class demonstration)

Grading Notice At this point, you might want to consult the following grade-action chart: Desired Grade in cs 1321 Actions You Will Take This Evening A Try numerous examples in Dr. Scheme AND the Stepper B Run Dr. Scheme, but not the Stepper C Merely read notes/slides D/F Blow it off until something’s due

Onto Functions We noted that Scheme is a “functional” programming language. This implies we’ll be working with functions. Let’s review what we knew about functions in mathematics.

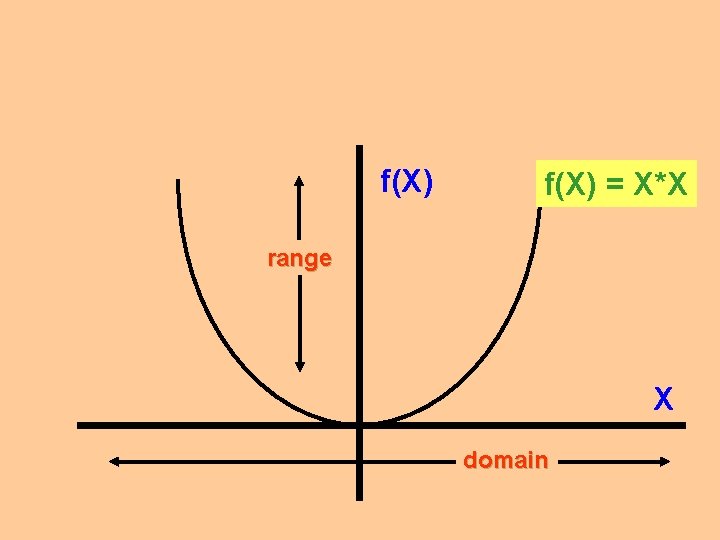
Functions Let’s start with a simple function from mathematics: f(x) = x * x This function squares a number, thus: f(2) = 2 * 2 = 4 f(5) = 5 * 5 = 25 with me?

Functions Recall that a function: domain 1 maps a set of values, called the domain, 2 onto a set of return values, called the range, range 3 so that one of the domain values is paired with one and only one of the range values.

f(X) = X*X range X domain

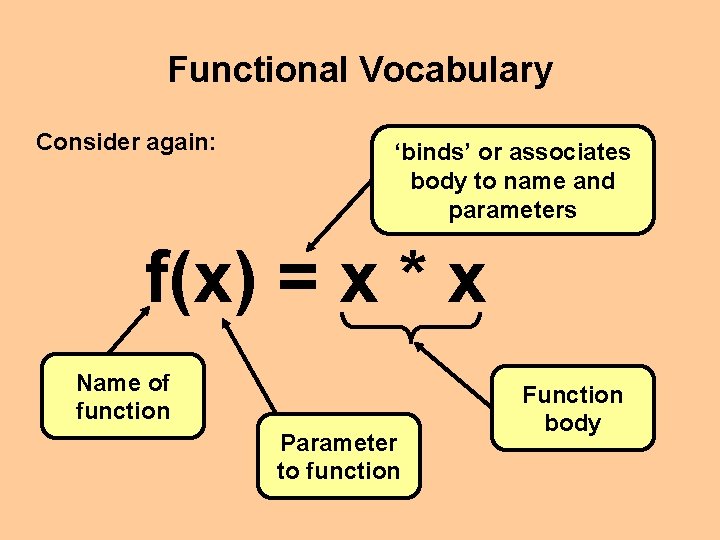
Functional Vocabulary Consider again: ‘binds’ or associates body to name and parameters f(x) = x * x Name of function Parameter to function Function body

Functional Vocabulary f(x) = x * x f(2) The function body is “applied to” to the value 2

Observations f(x) = x * x f(2) = 4 Predictable, reproducible. Each time we apply the function to the value 2, we get the same result. Nothing changed about the parameter Each time we call f(2), we do not change the value of 2. “The function doesn’t alter anything in the world. ”

Observations Composable We can compose a function of other functions. f(f(2)) The inner f(2) returns 4, so the outer f() call is sent 4. The overall expression returns 16: f(f(2)) f(4) 16

Basic Scheme Having refreshed our memory of functions, let’s learn about a few basic Scheme data types.

Scheme Elements Integers, Integers e. g. 4, -6, 0 Real Numbers, Numbers e. g. , 3. 14159 Ratios, Ratios e. g. , 1/2, 4/3 Symbols, Symbols e. g. , x, y, foo, bar -- often used for the name of a parameter, or a function name, or a variable

Scheme Given what we’ve covered, how would you categorize this: + Is this a real number? An integer? A ratio? Perhaps… a symbol? Hmm…

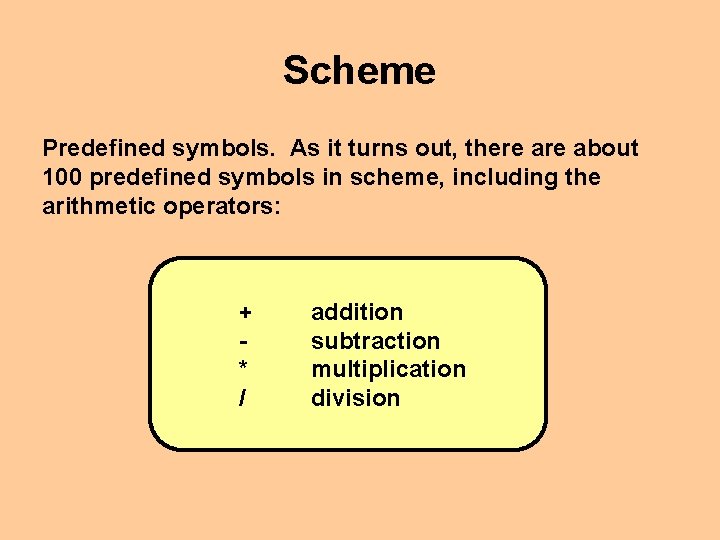
Scheme Predefined symbols. As it turns out, there about 100 predefined symbols in scheme, including the arithmetic operators: + * / addition subtraction multiplication division

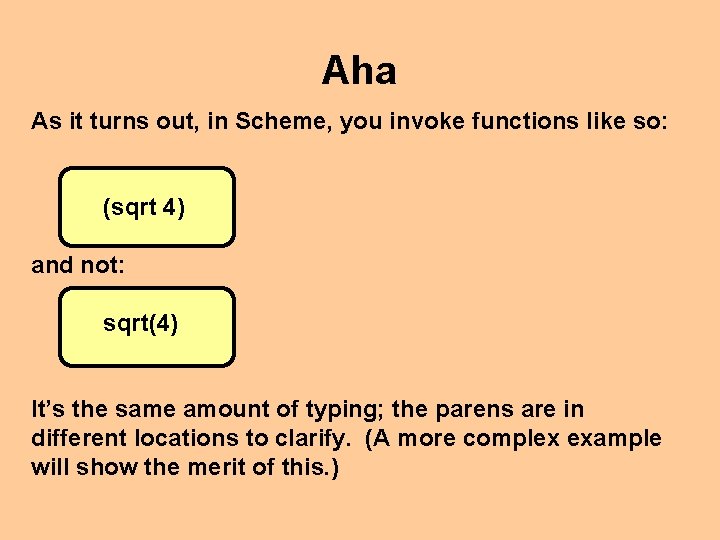
Our First Example Suppose we wished to use the predefined function “sqrt”, which returns the square root of a parameter. In the interpreter of Dr. Scheme, you might be tempted to type: sqrt(4) Since we’re used to expressions such as “f(4)” from mathematics – but Scheme uses a different style…

Aha As it turns out, in Scheme, you invoke functions like so: (sqrt 4) and not: sqrt(4) It’s the same amount of typing; the parens are in different locations to clarify. (A more complex example will show the merit of this. )

What if. . . When we next type in: (sqrt 4)) we see: #i 1. 4142135623730951 That looks like the right value, but what’s with the “#i” in front? This is scheme’s way of indicating an approximation.

So let's write a Scheme function! Remember square: f(x) = x * x We start by naming the function (define (sq x) and continue by adding the body (define (sq x) (* x x)) And we test (sq 3) 9

Remember Pythagoras?
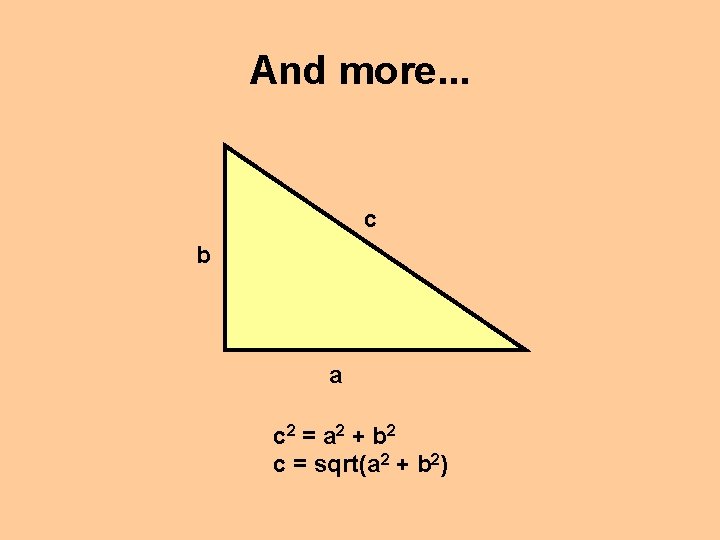
And more. . . c b a c 2 = a 2 + b 2 c = sqrt(a 2 + b 2)
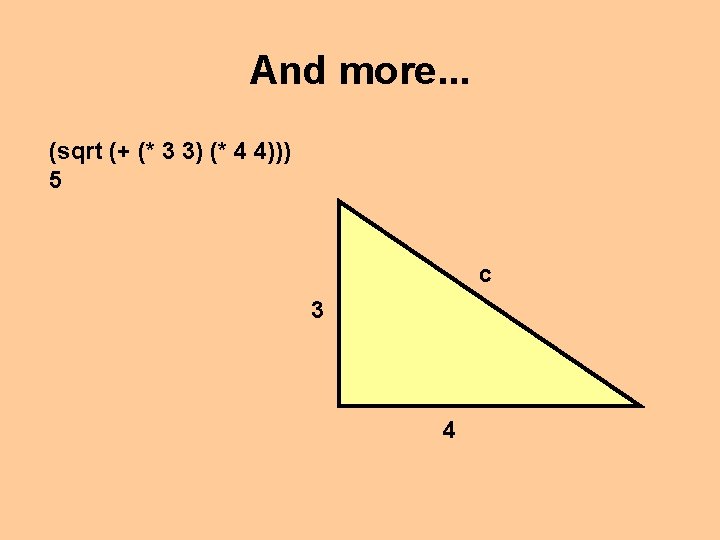
And more. . . (sqrt (+ (* 3 3) (* 4 4))) 5 c 3 4

Recall We use prefix notation, instead of infix: (* 3 3) rather than ( 3 * 3) because scheme expects the name of the function first (after the opening paren). "*" is a function that multiplies numbers together

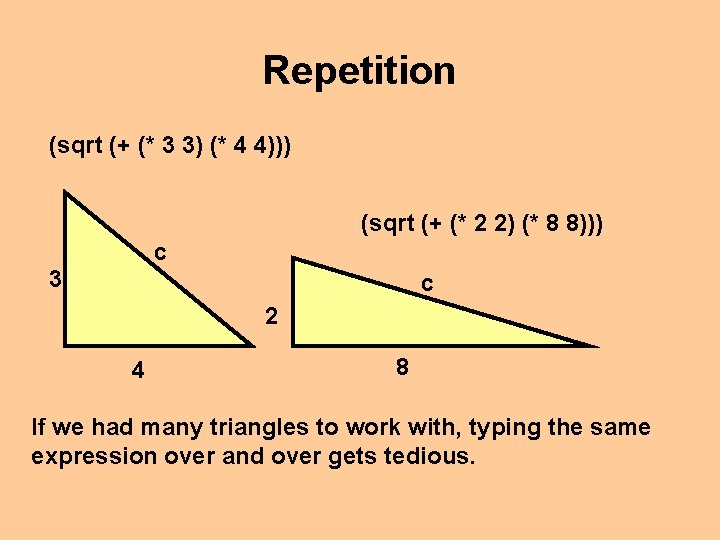
Repetition (sqrt (+ (* 3 3) (* 4 4))) (sqrt (+ (* 2 2) (* 8 8))) c 3 c 2 4 8 If we had many triangles to work with, typing the same expression over and over gets tedious.

A Fix In mathematics, we’d recognize the function at play: hypotenuse(a, b) = sqrt ( a*a + b*b ) Remember what that "=" sign meant? It binds the body to the function/parameter list. In Scheme, we can do this binding by ‘defining’ a function. It begins with: ( define

The Fix Is In At this point, the Scheme interpreter would expect you to name the function you hope to define. We need to come up with a symbol name. The symbol “hypotenuse” is good: (define (hypotenuse side 1 side 2) Here side 1 and side 2 are "parameters" or "arguments“ – basically placeholders for the side lengths

Still More At this point, we’ve have a symbol for the name of the function and the names of the parameters to the function. (define (hypotenuse side 1 side 2) The body of the function is easy to figure out: (define (hypotenuse side 1 side 2) (sqrt (+ (* side 1) (* side 2))))

Style matters! (not to scheme, but for good programming…) As a matter of style, we will use indents and returns to better format the statement: (define (hypotenuse side 1 side 2) (sqrt (+ (* side 1) (* side 2)))) As opposed to: (define (hypotenuse side 1 side 2) (sqrt (+ (* side 1) (* side 2))))

Can we abstract even further? Note that we need to square the values and we defined a square function: sq earlier. (define (hypotenuse side 1 side 2) (sqrt (+ (* side 1) (* side 2)))) (define (hypotenuse side 1 side 2) (sqrt (+ (sq side 1) (sq side 2))))

Questions?

Reading Assignment • Read Chapter 1 from How to Design Programs!!