Concise guide on numerical methods Grzegorz Pytel Warsaw

Concise guide on numerical methods Grzegorz Pytel, Warsaw University of Technology Fourier Transform and its applications

Talk scheme 1 2 3 Theoritcal introduction Numerical methods Applications Fourier transform and its application in review 29/10/2020 Fourier Transform and its application 2

1 THEORETICAL INTRODUCTION t Fourier Transform and its application 3

Fourier analysis Numerical methods Linear Periodic Phenomena Symmetry Group theory 29/10/2020 Fourier Transform and its application 4

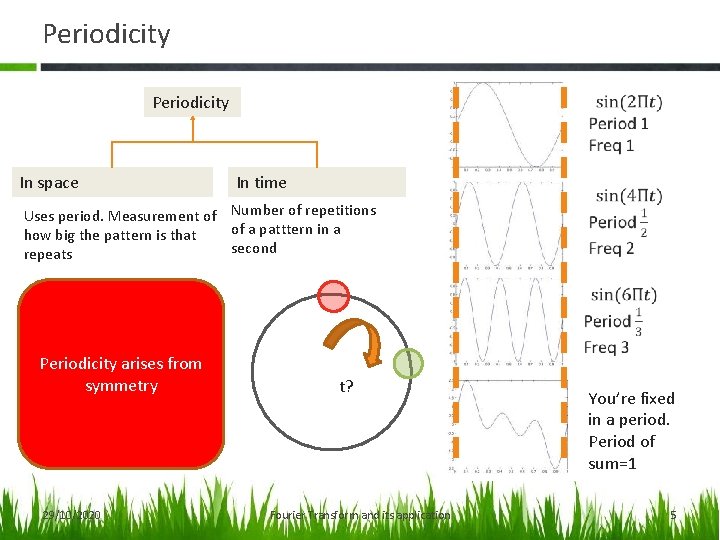
Periodicity In space In time Uses period. Measurement of Number of repetitions of a patttern in a how big the pattern is that second repeats Periodicity arises from symmetry 29/10/2020 t? Fourier Transform and its application You’re fixed in a period. Period of sum=1 5

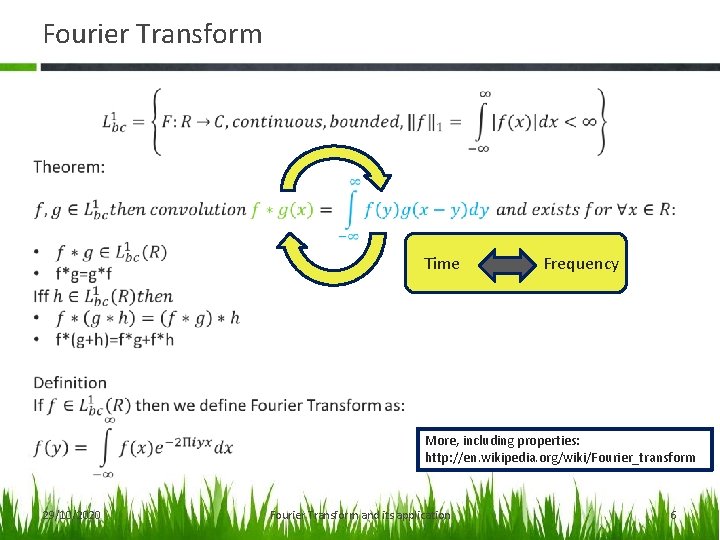
Fourier Transform Time Frequency More, including properties: http: //en. wikipedia. org/wiki/Fourier_transform 29/10/2020 Fourier Transform and its application 6

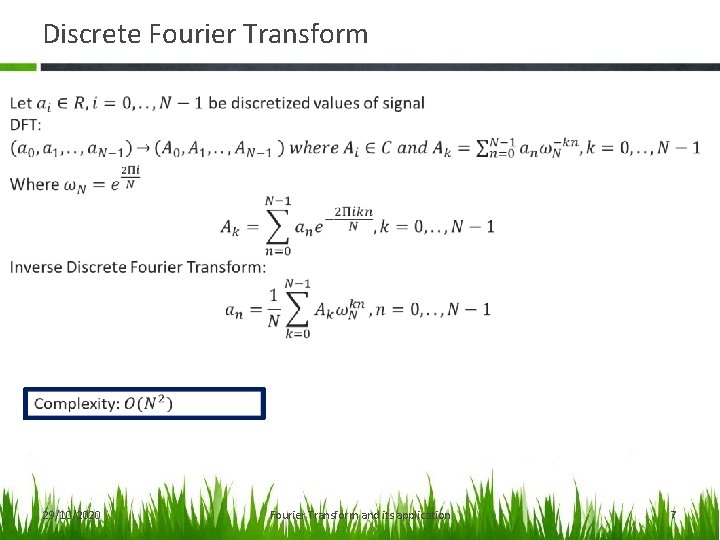
Discrete Fourier Transform 29/10/2020 Fourier Transform and its application 7

Fast Fourier Transform Wolfgang Bangerth, Guido Kanschat, • A fast Fourier transform (FFT) and Ralf Hartmann, a software library is an efficient algorithm to for computational solution of partial compute the discrete Fourier differential equations using adaptive transform (DFT) and its finite elements 2007 inverse. Jonathan Shewchuk for Triangle, a two • FFTs was constructed by J. W. dimensional mesh generator and Cooley of IBM and John W. Delaunay Triangulator Tukey of Princeton published a paper in 1965 reinventing the Chris Bischof and Alan Carle for ADIFOR algorithm and describing how 2. 0, an automatic differentiation tool for On Thursday, 8 July 1999, the third Wilkinson Prize to perform it conveniently on for Numerical Software was awarded to Matteo Frigo Fortran 77 programs a computer and Steven Johnson of Massachusetts Institute of Technology. The winning entry, FFTW (the "Fastest Fourier Linda Petzold for DASSL, a differential • http: //www. fftw. org/ Transform in the West"), is a library of C routines for the algebraic equation solver 29/10/2020 2003 1999 1995 1991 efficient computation of the discrete Fourier transform of real and complex data. The unparalleled efficiency over a wide range of computer platforms is by automatically determining the best computational strategy for the Wilkinson Prize axis particular hardware. Fourier Transform and its application 8

Fast Fourier Transform – Danielson Lenczos 29/10/2020 Fourier Transform and its application 9

2 Numerical methods World’s major methods used for computing FFT Fourier Transform and its application 10

Fast Fourier Transform Cooley– Tukey 29/10/2020 Primefactor Bruun's Rader's Fourier Transform and its application Bluestein's Winogard 11

Cooley-Tukley • Twiddle factor 29/10/2020 Danielson-Lanczos Cooley-Tukley Time [min] 140 0. 02 Task’s size 64 DFT 3– 5 significant digits, real numbers 2048 DFT 8 digits Fourier Transform and its application 12

Cooley-Tukley • Nlog. N complexity • Can only be used to speed the calculation of DFTs of a size that is a power of two • Requires padding with 0 • extra multiplications by roots of unity called twiddle factors More inc. sourcecode at: http: //numericalrecipes. blogspot. com/2009/04/cooleyturkey-fft-algorithm. html 29/10/2020 Fourier Transform and its application 13

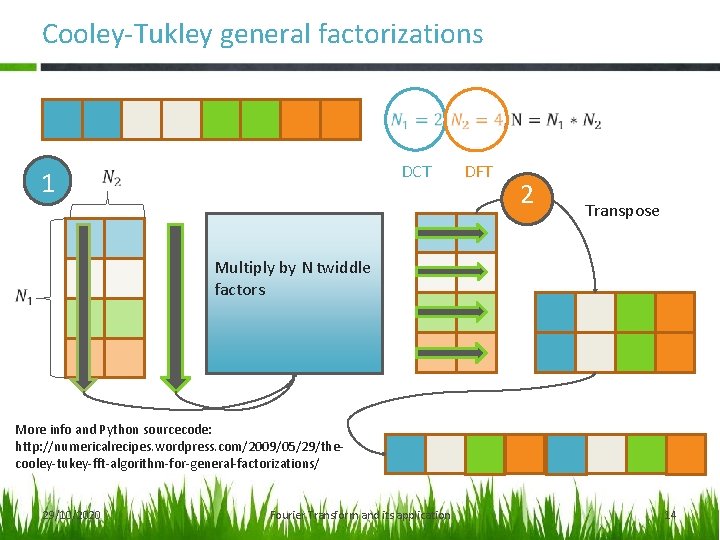
Cooley-Tukley general factorizations 1 DCT DFT 2 Transpose Multiply by N twiddle factors More info and Python sourcecode: http: //numericalrecipes. wordpress. com/2009/05/29/thecooley-tukey-fft-algorithm-for-general-factorizations/ 29/10/2020 Fourier Transform and its application 14

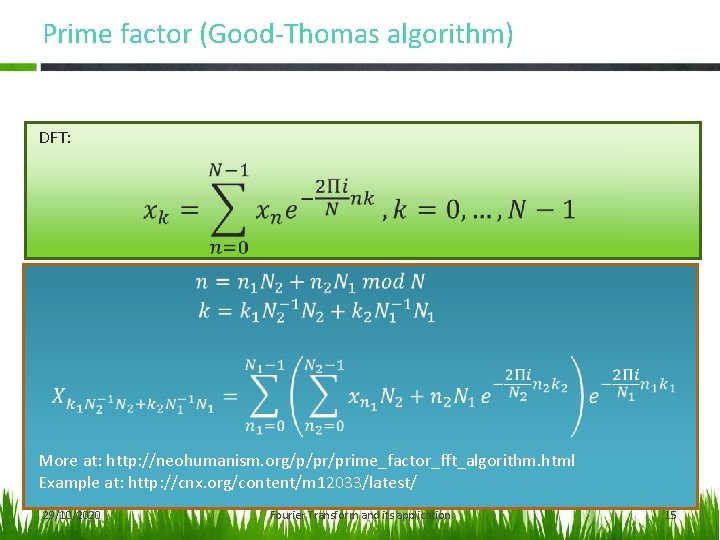
Prime factor (Good-Thomas algorithm) DFT: • More at: http: //neohumanism. org/p/pr/prime_factor_fft_algorithm. html Example at: http: //cnx. org/content/m 12033/latest/ 29/10/2020 Fourier Transform and its application 15

Bruun’s • Only real coefficients until the last computation stage • May be less accurate than Cooley–Tukey in the face of finite numerical precision (Storn, 1993) 29/10/2020 Fourier Transform and its application 16

Rader’s • Computes DFT of prime sizes by re-expressing the DFT as a cyclic convolution • Is a one-dimensional index-mapping scheme that turns a length-N DFT (N prime) into a length-(N− 1) convolution and a few additions. Rader's conversion works only for primelength N. • Most efficient for prime-length N More at: http: //cnx. org/content/m 12023/latest/ 29/10/2020 Fourier Transform and its application 17

Rader’s 29/10/2020 Fourier Transform and its application 18

Bluestein’s (1968) • Computes FFT at arbitrary sizes by re-expressing the DFT as a convolution • can be performed with a pair of FFTs (plus the precomputed FFT of bn) via the convolution theorem. The key point is that these FFTs are not of the same length N: such a convolution can be computed exactly from FFTs only by zero-padding it to a length greater than or equal to 2 N– 1 • O(N log N) 29/10/2020 Fourier Transform and its application 19

Winogard DFT’s row • • DFT’s column Fastest, smallest number of operations Extremely efficient for small N (N<20) The number of adds becomes huge for large N Most difficult Winogard need O(N) multiplications to compute the FFT. However, at the cost of asymptotically many more additions, and thus they represent a tradeoff that is typically unfavorable on modern CPUs with hardware multipliers. More at: http: //cnx. org/content/m 16333/latest/#uid 24 29/10/2020 Fourier Transform and its application 20

3 Industrial applications Examples of industrial applications of FFT and DFT Fourier Transform and its application 21

Industrial products/companies reliable on FFT 29/10/2020 Fourier Transform and its application 22

Voice power in matlab DEMO 29/10/2020 Fourier Transform and its application 23

DEMO Source code function [n, fs, wave. Data] = wave. Record. FFT() n=20000; fs=11025; wave. Data=wavrecord(n, fs); wavplay(wave. Data, fs); frequency(wave. Data, n, fs); End 29/10/2020 Fourier Transform and its application function[] = frequency(wave. Data, n, fs) s 1=wave. Data(: , 1); p=fft(s 1); n. Unique. Pts=ceil((n+1)/2); p=p(1: n. Unique. Pts); p=abs(p); p=p/n; p=p. ^2; if rem(n, 2) p(2: end) = p(2: end)*2; else p(2: end -1) = p(2: end - 1)*2; end freq. Array=(0: n. Unique. Pts-1)*(fs/n); plot(freq. Array/1000, 10*log 10(p), 'k') xlabel('Frequency (k. Hz)') ylabel('Power (d. B)') end 24

Fourier transform DIGITIZING NATURE 29/10/2020 Fourier Transform and its application 25

End remarks FFT length Multiplies Adds Mults+Adds 10248 30728 40976 • Radix 2 The most commonly used FFT algorithms by Split radix 1024 7172 27652 34842 far are the power-of-two-length FFT Prime factor 1008 5804 29100 34904 algorithms Winograd 1008 3548 34416 37964 • Prime Factor and Winograd require somewhat fewer multiplies, but the overall difference usually isn't sufficient to warrant the extra difficulty • Changing radix can speed up, up to 30 -40 % 29/10/2020 Fourier Transform and its application 26

Bibliography 29/10/2020 • http: //see. stanford. edu/see/co urseinfo. aspx? coll=84 d 174 c 2 d 74 f-493 d-92 ae-c 3 f 45 c 0 ee 091 Fourier Transform and its application 27