Colorao Teoria dos Grafos INF 5037INF 2781 CCECPPGIUFES

Coloração Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

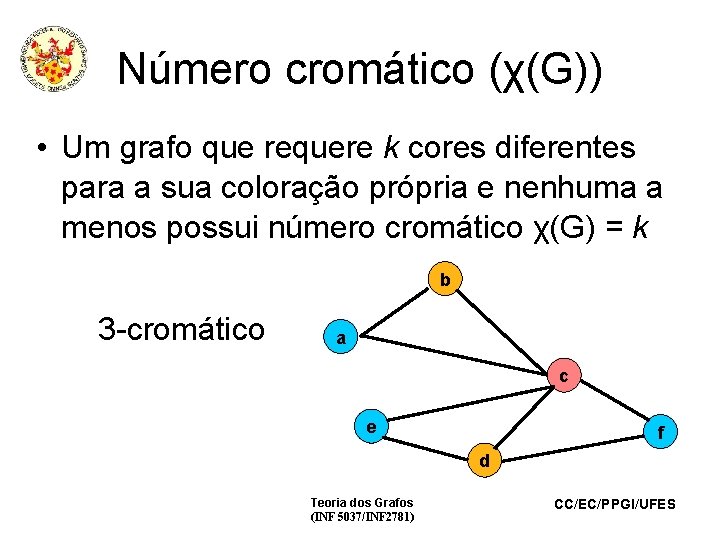
Número cromático (χ(G)) • Um grafo que requere k cores diferentes para a sua coloração própria e nenhuma a menos possui número cromático χ(G) = k b 3 -cromático a c e f d Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

Um exemplo de aplicação • Problema dos exames: alocação de um grupo de alunos aos exames de recuperação que eles devem prestar em um colégio » Restrição: Duas disciplinas só podem ter exames realizados simultaneamente se não envolverem alunos em comum Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

Um exemplo de aplicação Alunos Disciplinas 1 Mat. x Port. x 2 3 4 5 6 7 8 9 10 11 x x Hist. x Física x Química x Biologia x 14 15 x x x 16 x x Ingl. x 13 x x Geog. 12 x x x x x Teoria dos Grafos (INF 5037/INF 2781) x x CC/EC/PPGI/UFES

Um exemplo de aplicação São necessários apenas dois horários para realização dos exames: um para os exames de Matemática, Geografia, Biologia e História e outro, para os exames de Português, Inglês, Física e Química. Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

Teorema Toda árvore com dois ou mais vértices é 2 -cromática Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

Teorema Um grafo com pelo menos uma aresta é 2 -cromático sss não possui ciclos comprimento ímpar Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

Teorema Seja Δ o grau máximo dos vértices de G. Então χ(G) 1 + Δ Exercício! Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

Partição Cromática • Um grafo G k-cromático é p-partido sss k p. • Em um grafo p-partido, vértices de uma mesma partição não são adjacentes. • Um conjunto de vértices de um grafo é dito independente se não possui vértices adjacentes. Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

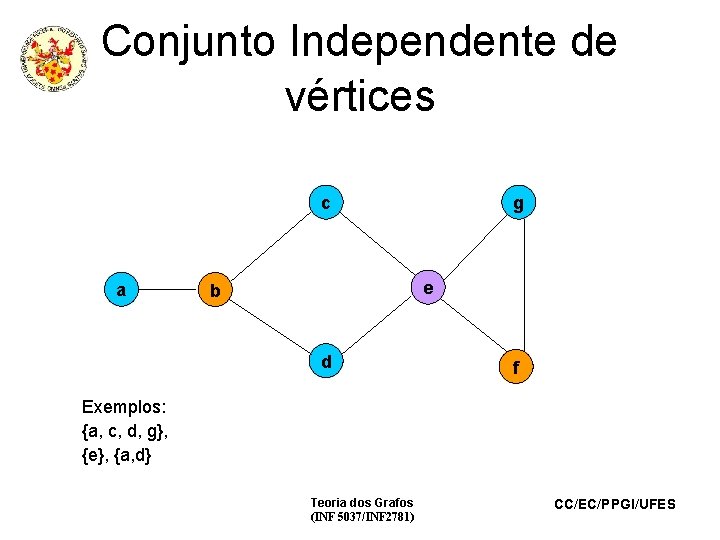
Conjunto Independente de vértices c a g e b d f Exemplos: {a, c, d, g}, {e}, {a, d} Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

Conjunto Independente de vértices maximal Um conjunto independente maximal é um conjunto independente no qual não se pode adicionar mais nenhum vértice sem destruir a propriedade de independência. Exemplos: {a, c, d, g}, {b, f} Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

Conjunto Independente de vértices maximal • Existem vários conjuntos independentes maximais em um grafo que podem ter diferentes tamanhos. • Qual é o de maior tamanho? • (G) = número de independência de G (cardinalidade do conjunto independente de vértices de maior tamanho de G) Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

χ(G) X (G) • Seja G um grafo com n vértices e χ(G) = k • Número de vértices coloridos com a mesma cor (G) ≥ n/ χ(G) Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

Como achar um conjunto independente maximal? • Comece com um vértice qualquer. • Selecione os próximos vértices sempre testando se o conjunto ao qual eles estão sendo inseridos continua independente • Atenção: encontra-se um conjunto maximal e não o maior de todos! Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

χ(G) X (G) • Encontrar (G): consiste em encontrar todos os conjuntos independentes maximais e obter o maior; • Encontrar χ(G): número mínimo de conjuntos independentes maximais cuja união resulta em V Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

Partição cromática • Dado um grafo simples e conexo G, os vértices de G são particionados no menor número possível de conjuntos independentes de vértices disjuntos. Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

Matchings Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

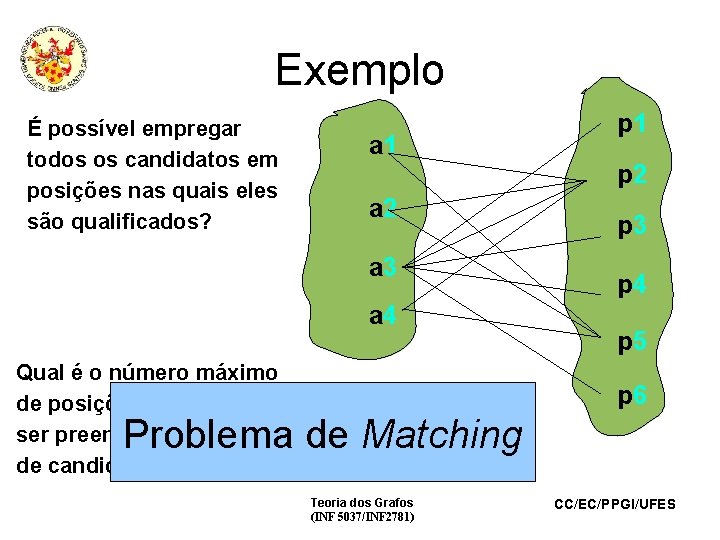
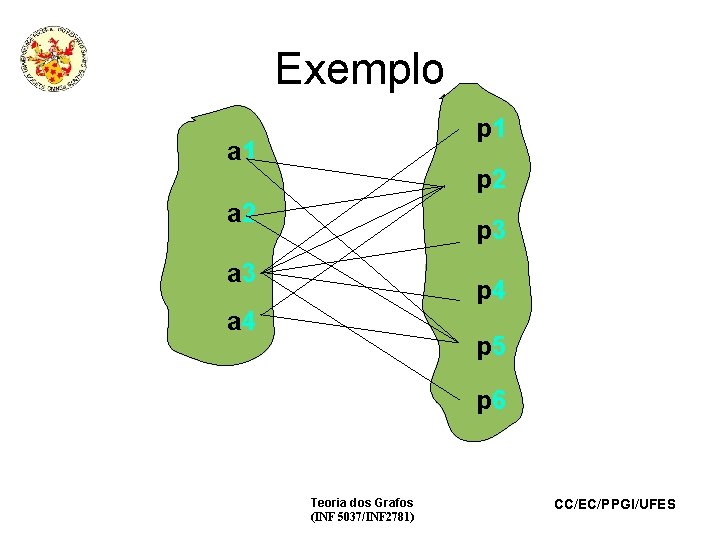
Exemplo • Sejam a 1, a 2, a 3 e a 4 candidatos a preencher 6 vagas p 1, p 2, p 3, p 4, p 5 e p 6 de uma empresa. A qualificação de cada candidato o possibilita a se candidatar para um certo subconjunto de vagas, conforme a figura a seguir: Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

Exemplo É possível empregar todos os candidatos em posições nas quais eles são qualificados? a 1 a 2 a 3 a 4 Qual é o número máximo de posições que podem ser preenchidas pelo grupo de candidatos? p 1 p 2 p 3 p 4 p 5 p 6 Problema de Matching Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

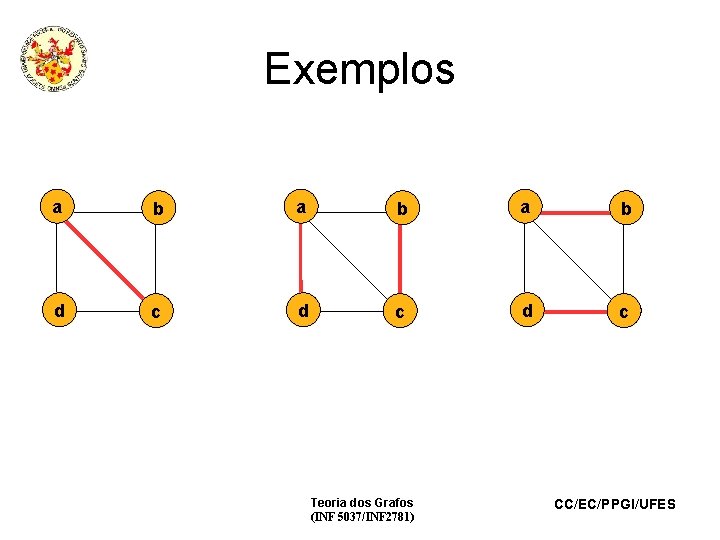
Matching • Um matching em um grafo é um subconjunto de arestas não adjacentes. Uma única aresta já é considerada um matching. • Um matching maximal é um matching no qual nenhuma aresta a mais pode ser adicionada sem ferir a propriedade de matching Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

Exemplos a b a b d c d c Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

Número de matching • Um grafo pode ter muitos matchings maximais; • n° de matching: o número de arestas do maior deles. • qual é o número de matching do grafo do slide anterior? Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

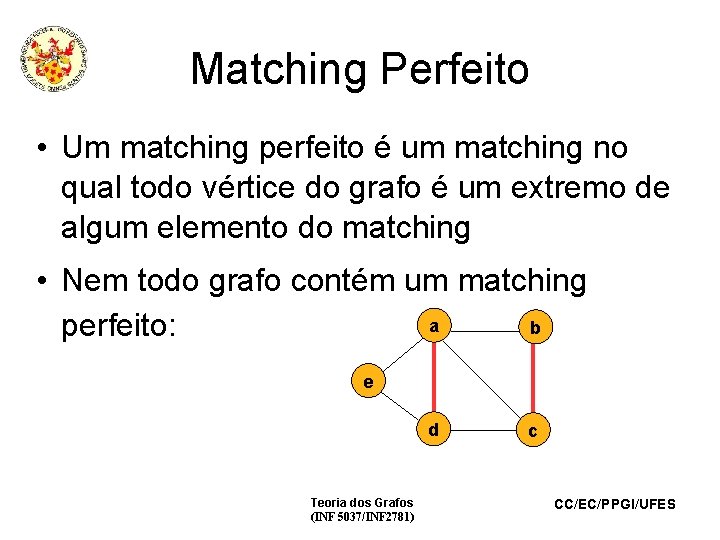
Matching Perfeito • Um matching perfeito é um matching no qual todo vértice do grafo é um extremo de algum elemento do matching • Nem todo grafo contém um matching a b perfeito: e d Teoria dos Grafos (INF 5037/INF 2781) c CC/EC/PPGI/UFES

Observação Todo matching perfeito é maximal mas nem todo matching maximal é perfeito Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

Matching completo • Definição válida para grafos bipartidos • Em um grafo bipartido com subconjuntos de vértices V 1 e V 2, um matching completo de V 1 em V 2 é um matching no qual existe uma aresta incidente a cada aresta de V 1. Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

Observação um matching completo é o maior matching maximal mas um matching maximal pode não ser completo Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

Exemplo p 1 a 1 p 2 a 2 p 3 a 3 p 4 a 4 p 5 p 6 Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

Condições para existência de um matching completo • |V 1| |V 2|; • todo subconjunto de r vértices em V 1 deve ser adjacente a pelo menos r vértices em V 2, para r = 1, 2, . . . , |V 1|. Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

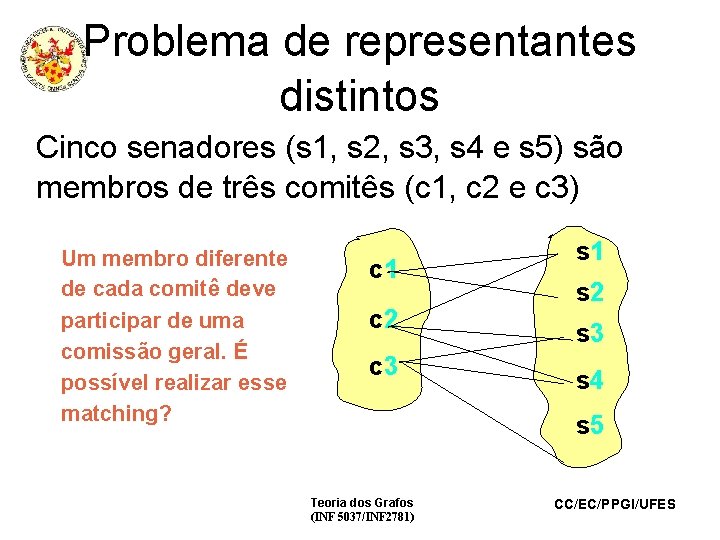
Problema de representantes distintos Cinco senadores (s 1, s 2, s 3, s 4 e s 5) são membros de três comitês (c 1, c 2 e c 3) Um membro diferente de cada comitê deve participar de uma comissão geral. É possível realizar esse matching? c 1 c 2 c 3 s 1 s 2 s 3 s 4 s 5 Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

Teorema Em um grafo bipartido, um matching completo de V 1 para V 2 existe se existe um inteiro positivo m tal que o grau de todo vértice v 1 de V 1 ≥ m ≥ o grau de todo vértice v 2 de V 2 Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

Prova • Considere um subconjunto de r vértices em V 1 • Cada um dos r vértices tem pelo menos m vértices de V 2 incidentes a ele. Assim esses r vértices tem pelo menos m. r arestas incidentes • Cada uma das m. r arestas é incidente a algum vértices de V 2 • Por sup. d(vi) ≤ m, vi de V 2 • Então as m. r arestas são incidentes a pelo menos m. r/m = r vértices • Assim, qualquer subconjunto de r vértices de V 1 é adjacente a r ou mais vértices de V 2. • Logo, G possui um matching completo Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

Cobertura de vértices • Um conjunto de vértices K de V é uma cobertura de G se toda aresta de G possui pelo menos um extremo em K • Cobertura mínima: aquela que possui o menor número possível de vértices Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

Exemplo Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

Observações • Se K é uma cobertura e M um matching de G então K contém pelo menos um extremo de cada aresta de M • Para quaisquer K e M em G tem-se |M| |K| Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

Cobertura de arestas • Em um grafo G, um conjunto g de arestas cobre G se todo vértice em G é incidente a pelo menos uma aresta em g. O conjunto g é chamado cobertura de G. Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

Observações • G consiste na sua própria cobertura • Uma árvore geradora é uma cobertura • Um ciclo hamiltoniano, se ele existe, é uma cobertura Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

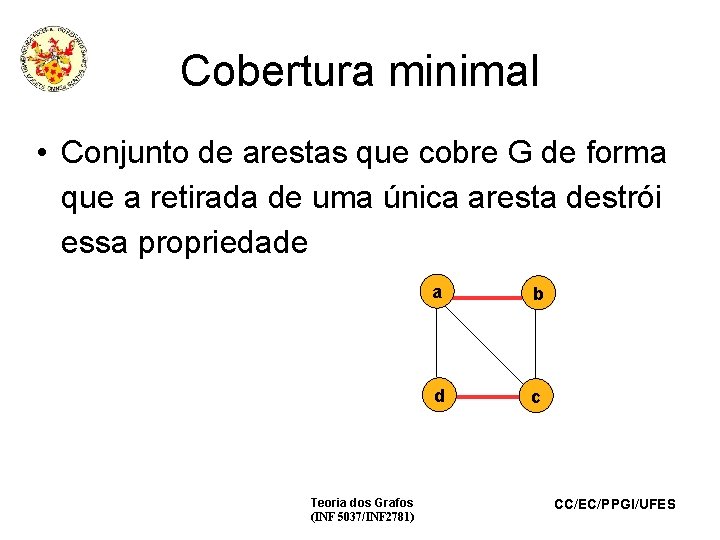
Cobertura minimal • Conjunto de arestas que cobre G de forma que a retirada de uma única aresta destrói essa propriedade Teoria dos Grafos (INF 5037/INF 2781) a b d c CC/EC/PPGI/UFES

Observações • G possui uma cobertura se não possui vértices isolados • Uma cobertura de um grafo com n vértices possui pelo menos n/2 arestas • Toda aresta pendente de um grafo faz parte de toda cobertura de G • Toda cobertura contém uma cobertura minimal • Nenhuma cobertura minimal contém um ciclo. Assim, uma cobertura minimal contém no máximo n-1 arestas Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

Nº de cobertura de G • Número de arestas da cobertura minimal de menor tamanho de G Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES

Teorema Uma cobertura g de um grafo é minimal se e somente se g não contém caminhos de comprimento 3 ou mais Teoria dos Grafos (INF 5037/INF 2781) CC/EC/PPGI/UFES