rvores CCECMestrado Teoria dos Grafos UFES rvores Grafo

Árvores CC/EC/Mestrado Teoria dos Grafos UFES

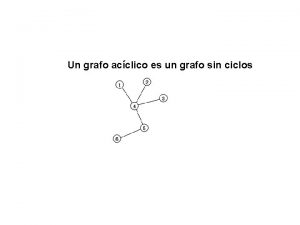
Árvores • Grafo Acíclico: não possui ciclos CC/EC/Mestrado Teoria dos Grafos UFES

Árvores • Grafo Acíclico: não possui ciclos • Uma árvore é um grafo conexo acíclico CC/EC/Mestrado Teoria dos Grafos UFES

Árvores • Grafo Acíclico: não possui ciclos • Uma árvore é um grafo conexo acíclico Todas as árvores com 6 vértices CC/EC/Mestrado Teoria dos Grafos UFES

Floresta Um grafo acíclico é também chamado de floresta. CC/EC/Mestrado Teoria dos Grafos UFES

Teorema: Um grafo T é uma árvore sss existir um único caminho entre cada par de vértices de T CC/EC/Mestrado Teoria dos Grafos UFES

Prova • ( ) Por contradição!!! – T é uma árvore • v e w dois vértices quaisquer de T – não existe caminho entre v e w ou – P 1 e P 2: dois caminhos-(u, v) distintos » Existem necessariamente dois vértices t 1 e t 2 P 1 e P 2 tais que entre t 1 e t 2, P 1 e P 2 são distintos CC/EC/Mestrado Teoria dos Grafos UFES

Prova • ( ) Também por contradição!!! – existe um único caminho entre cada par de vértices: T é conexo – Sup. T não é acíclico: • existe um ciclo C em T • seja {v, w} uma aresta de C: – Dois caminhos entre v e w em T (contradição) CC/EC/Mestrado Teoria dos Grafos UFES

Teorema: Se T é uma árvore então m=n-1 Prova: • Por indução em n!!!! CC/EC/Mestrado Teoria dos Grafos UFES

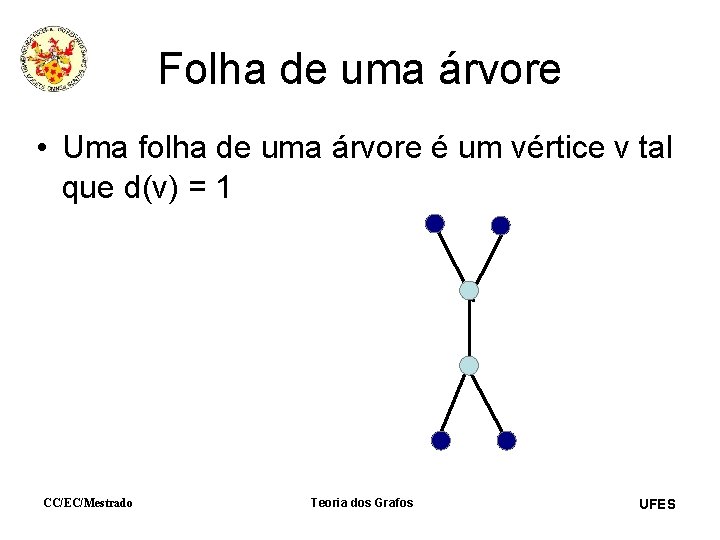
Folha de uma árvore • Uma folha de uma árvore é um vértice v tal que d(v) = 1 CC/EC/Mestrado Teoria dos Grafos UFES

Teorema Toda árvore possui pelo menos duas folhas, n > 1. CC/EC/Mestrado Teoria dos Grafos UFES

Teorema: Um grafo conexo é uma árvore sss toda aresta é uma ponte CC/EC/Mestrado Teoria dos Grafos UFES

Teorema: O centro de uma árvore possui um ou dois vértices. CC/EC/Mestrado Teoria dos Grafos UFES

Árvore enraizada • Uma árvore no qual um vértice é destacado dos outros (raíz) é chamada de árvore com raíz ou enraizada. • Nível de uma árvore enraizada: um vértice vi é dito estar no nível i da árvore se vi está a uma distância i da raiz. • Altura: nível máximo da árvore CC/EC/Mestrado Teoria dos Grafos UFES

Teorema: Toda árvore é um grafo bipartido. Exercício!!! CC/EC/Mestrado Teoria dos Grafos UFES

Árvore binária • Uma árvore estritamente binária é uma classe especial de árvore enraizada • Cada vértice possui exatamente 2 filhos, ou seja, existe apenas um vértice com grau 2 (raíz) e os outros vértices possuem grau 1 ou 3 CC/EC/Mestrado Teoria dos Grafos UFES

Árvore binária • Propriedades: – a) o número de vértices é ímpar – b) o número de folhas é (n+1)/2 – c) a altura mínima de uma árvore estritamente binária com n vértices é log 2 (n+1) - 1 CC/EC/Mestrado Teoria dos Grafos UFES

Subgrafo gerador • Relembrando: um grafo H é subgrafo de G se V(H) V(G) e E(H) E(G). Se V(H) = V(G) então H é subgrafo gerador ou de espalhamento de G. CC/EC/Mestrado Teoria dos Grafos UFES

Árvore Geradora • Uma árvore geradora é um subgrafo gerador de G que é uma árvore. • Uma árvore geradora em um grafo G é um subgrafo minimal que conecta todos os vértices de G; CC/EC/Mestrado Teoria dos Grafos UFES

Teorema: Todo grafo conexo possui uma árvore geradora CC/EC/Mestrado Teoria dos Grafos UFES

Corolário: Se G é conexo, então m n-1 CC/EC/Mestrado Teoria dos Grafos UFES

Teorema: Seja T uma árvore geradora de um grafo conexo G e seja a uma aresta de G, a T. Então T+ a contém um único ciclo. CC/EC/Mestrado Teoria dos Grafos UFES

Prova: • Como T é acíclico, cada ciclo de T+a contém a. C é um ciclo de T+e sse C-e é um caminho em T ligando os extremos de e. Pelo teorema, T tem um único caminho desse tipo, logo T+e contém um único ciclo. CC/EC/Mestrado Teoria dos Grafos UFES

Algoritmos • Para construção de uma árvore geradora; • Para construção de uma árvore geradora mínima. CC/EC/Mestrado Teoria dos Grafos UFES

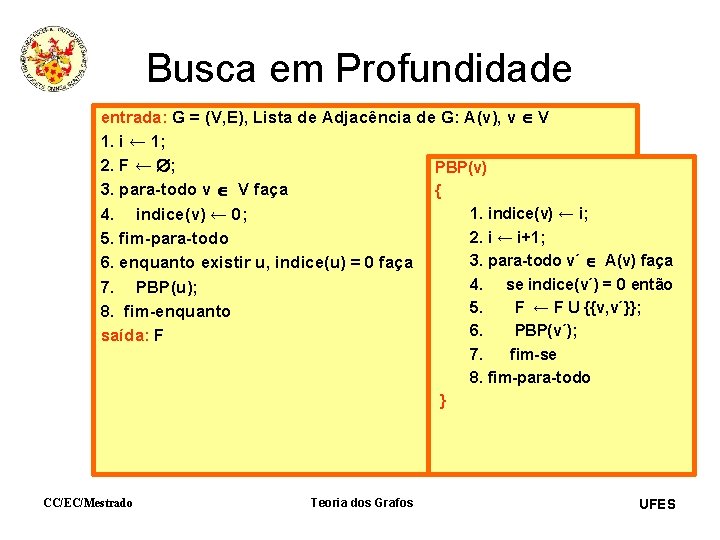
Busca em Profundidade entrada: G = (V, E), Lista de Adjacência de G: A(v), v V 1. i ← 1; 2. F ← ; PBP(v) 3. para-todo v V faça { 1. indice(v) ← i; 4. indice(v) ← 0; 2. i ← i+1; 5. fim-para-todo 3. para-todo v´ A(v) faça 6. enquanto existir u, indice(u) = 0 faça 4. se indice(v´) = 0 então 7. PBP(u); 5. F ← F U {{v, v´}}; 8. fim-enquanto 6. PBP(v´); saída: F 7. fim-se 8. fim-para-todo } CC/EC/Mestrado Teoria dos Grafos UFES

Complexidade • Para cada v V, PBP(v) é chamado apenas uma vez quando o vértice ainda não foi visitado (indice(v) = 0) • Tempo gasto por PBP(v): proporcional a d(v) • Tempo gasto por todas as chamadas de PBP(v): proporcional a m • Linhas 3 – 8: O(n) • Construção de F: O(m) • Complexidade: O(max {n, m}) CC/EC/Mestrado Teoria dos Grafos UFES

Árvores geradoras em um grafo valorado • O peso de uma árvore geradora T de G é definido como a soma dos valores de todas as arestas de T. • Diferentes árvores geradoras de T podem ter diferentes pesos. • Árvore Geradora mínima: a árvore geradora de G de menor peso. CC/EC/Mestrado Teoria dos Grafos UFES

Árvore geradora mínima • Aplicações: – Em problemas de interligação (comunicação, redes de luz, esgotos, etc. ) – Em problemas de construção de redes de menor custo (malhas rodoviárias, redes de computadores) CC/EC/Mestrado Teoria dos Grafos UFES

Teorema: Uma árvore geradora T de um grafo conexo valorado G é mínima sss não existe qualquer outra árvore geradora de G, a uma distância 1 de T, cujo peso é menor que o peso de T. Distância entre Ti e Tj de G: número de arestas de G presentes em Ti mas não presentes em Tj. CC/EC/Mestrado Teoria dos Grafos UFES

Algoritmo de Prim entrada: G = (V, E), Lista de Adjacência de G: A(v), v V, matriz de pesos 1. T ← ; 2. V´ ← {u}; 3. para-todo v V – V´ faça 4. L(v) ← peso ({u, v}); 5. fim-para-todo 6. enquanto V´ V faça 7. ache um vértice w tal que L(w) = min {L(v)| v V-V´}; 8. u = o vértice de V´, ligado a w, representando a aresta com o menor custo; 9. e = {u, w}; 10. T ← T U {e}; 11. V´← V´ U {w}; 12. para-todo v V – V´ faça 13. se peso({v, w}) < L(v) então 14. L(v) ← p({v, w}); 15. 16. fim-se fim-para-todo 17. fim-enquanto saída: T CC/EC/Mestrado Teoria dos Grafos UFES

Complexidade • Linhas 6 - 16: n-1 vezes • Linhas 7 - 8: n-1 vezes • Linhas 11 – 15: n-1 vezes • Complexidade: O(n 2) CC/EC/Mestrado Teoria dos Grafos UFES

Teorema: O algoritmo de Prim acha uma árvore geradora mínima de um grafo conexo G não orientado. CC/EC/Mestrado Teoria dos Grafos UFES

Algoritmo de Kruskal entrada: G = (V, E), Lista de Adjacência de G: A(v), v V, matriz de pesos 1. se peso (ei) > peso (ej) então 2. i > j; 3. fim-se // ordenar as arestas pelos pesos 4. T ← ; 5. para-todo i = 1, . . . , |E| faça 6. se T U {e} é acíclico então 7. T ← T U {e}; 8. fim-se 9. fim-para-todo; saída: T CC/EC/Mestrado Teoria dos Grafos UFES

Complexidade • Exercício!! CC/EC/Mestrado Teoria dos Grafos UFES