LICEO SCIENTIFICO con annesso LICEO CLASSICO F QUERCIA

LICEO SCIENTIFICO con annesso LICEO CLASSICO “F. QUERCIA” di Marcianise Dirigente Scolastico: Prof. DIAMANTE MAROTTA Pro gett o la uree scie ntif iche DI MARSILIO CARMELA MADONNA Docenti Cordinatori: Prof. ssa Concetta Marino Prof. Renzo Piccolo MARTONE IV C MARIADOMENICA IV A RAFFAELLA MIGLIORINI SONIA IV C IV D 1

Laboratorio di Teoria dei Grafi

La teoria dei grafi è quella disciplina che ha come oggetto di studio i grafi che permettono di schematizzare una grande varietà di situazioni e di processi e spesso di consentire di analizzarli in termini quantitativi ed algoritmici. Essa trova applicazione in numerosi campi che vanno dalla topologia all’informatica, ma anche nel quotidiano. Grafo sociale

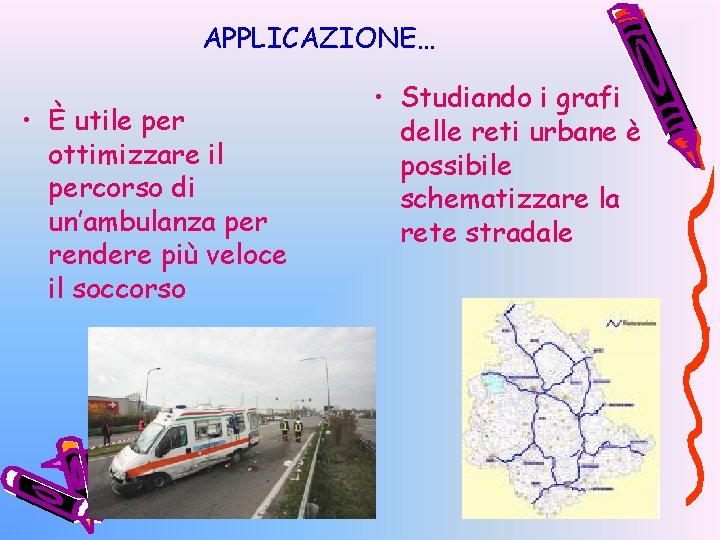
APPLICAZIONE… • È utile per ottimizzare il percorso di un’ambulanza per rendere più veloce il soccorso • Studiando i grafi delle reti urbane è possibile schematizzare la rete stradale

LA TEORIA DEI GRAFI TROVA APPLICAZIONI ANCHE IN ALTRI CAMPI… • In sociologia • In chimica contribuisce alla schematizzare le rappresentazione relazioni che delle molecole più intercorrono tra gli complesse. individui.

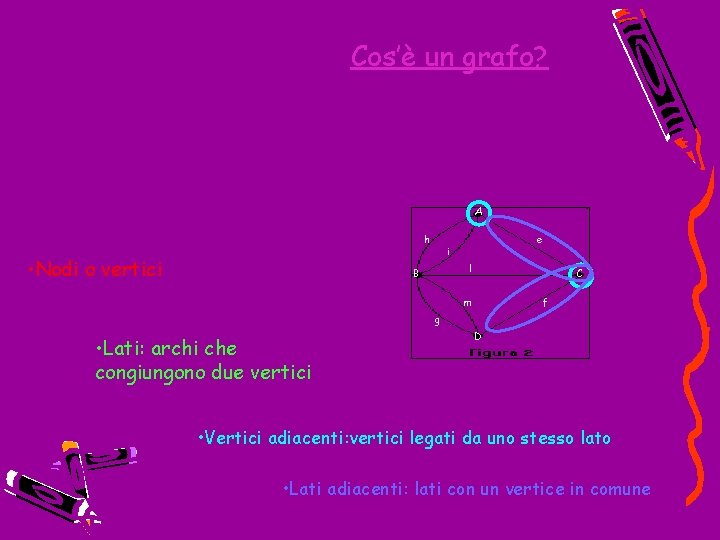
Cos’è un grafo? A h • Nodi o vertici e i l B C m f g • Lati: archi che congiungono due vertici D • Vertici adiacenti: vertici legati da uno stesso lato • Lati adiacenti: lati con un vertice in comune

Parametri di un grafo: In questo grafo è • Ordine: è il numero di vertici 4 perché i vertici sono: A; B; C; D • Dimensione: è il numero di lati 7 perché i lati sono: e; f; g; h; i; l; m • Grado o valenza di un vertice: è il numero dei lati passanti per il vertice e si indica con d(v). A h e i l B • Lemma della stretta di mano: la somma dei gradi di ciascun vertice è il doppio del numero dei lati Ad(v)+ Bd(v)+ Cd(v)+ Dd(v)= 2 • (n lati) 3 + 5 + 3 = 2 • 7 C m g f D 7 lati 4 vertici

Tipi di grafi connessi (comunque siano presi due vertici esiste un lato che li unisce): • Grafo semplice: formato da una successione senza ripetizione di una coppia vertice-lato. A B C • Multigrafo: se almeno un vertice del grafo ha più di un vertice adiacente A D E E B • Grafo orientato: i lati hanno un senso di percorrenza (A->B non equivale a B->A) Grafo non orientato: i lati non hanno un senso di percorrenza (A->B equivale a B->A) A B C C E Grafo diretto: se è multigrafo e orientato A B D E C C D A Un grafo è completo quando ogni vertice è collegato con tutti gli altri

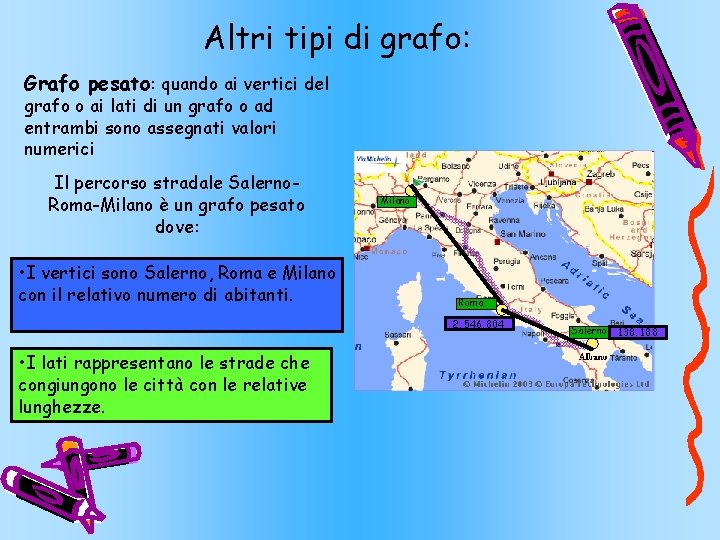
Altri tipi di grafo: Grafo pesato: quando ai vertici del grafo o ai lati di un grafo o ad entrambi sono assegnati valori numerici Il percorso stradale Salerno. Roma-Milano è un grafo pesato dove: • I vertici sono Salerno, Roma e Milano con il relativo numero di abitanti. Milano Roma 2. 546. 804 • I lati rappresentano le strade che congiungono le città con le relative lunghezze. Salerno 138. 188

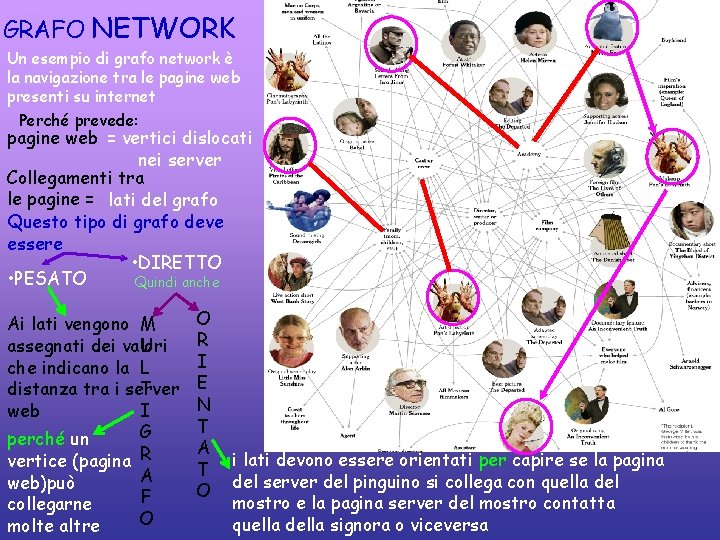
GRAFO NETWORK Un esempio di grafo network è la navigazione tra le pagine web presenti su internet Perché prevede: pagine web = vertici dislocati nei server Collegamenti tra le pagine = lati del grafo Questo tipo di grafo deve essere • DIRETTO • PESATO Quindi anche Ai lati vengono M assegnati dei valori U che indicano la L distanza tra i server T web I G perché un vertice (pagina R A web)può F collegarne O molte altre O R I E N T A T O i lati devono essere orientati per capire se la pagina del server del pinguino si collega con quella del mostro e la pagina server del mostro contatta quella della signora o viceversa

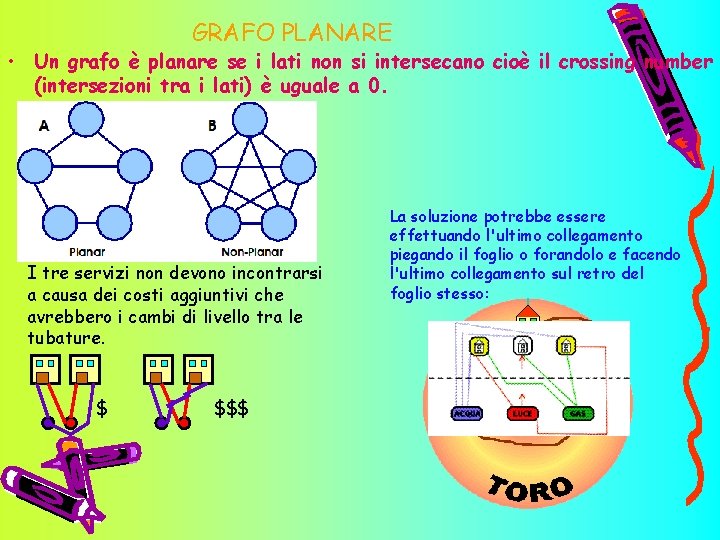
GRAFO PLANARE • Un grafo è planare se i lati non si intersecano cioè il crossing number (intersezioni tra i lati) è uguale a 0. I tre servizi non devono incontrarsi a causa dei costi aggiuntivi che avrebbero i cambi di livello tra le tubature. $ $$$ La soluzione potrebbe essere effettuando l'ultimo collegamento piegando il foglio o forandolo e facendo l'ultimo collegamento sul retro del foglio stesso:

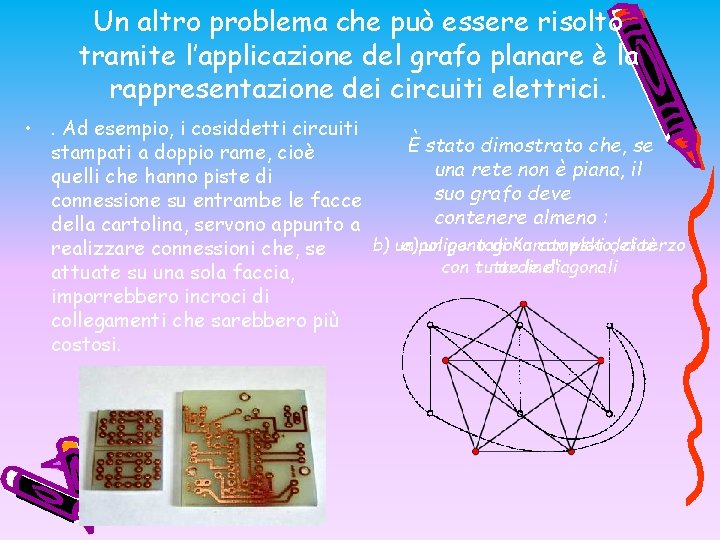
Un altro problema che può essere risolto tramite l’applicazione del grafo planare è la rappresentazione dei circuiti elettrici. • . Ad esempio, i cosiddetti circuiti È stato dimostrato che, se stampati a doppio rame, cioè una rete non è piana, il quelli che hanno piste di suo grafo deve connessione su entrambe le facce contenere almeno : della cartolina, servono appunto a b) un a) poligono un pentagono di Kuratowski completo, del cioè terzo realizzare connessioni che, se con tutte ordine" le diagonali attuate su una sola faccia, imporrebbero incroci di collegamenti che sarebbero più costosi.

Si può dimostrare che per un grafo planare connesso e semplice con numero di vertici maggiore o uguale a 3 vale la seguente relazione : m<3 n-6 n = numero di vertici, . m = numero di lati Se n è maggiore di tre e non vi sono cicli di lunghezza tre, allora il numero di lati è minore o uguale a 2 m<2 n-4

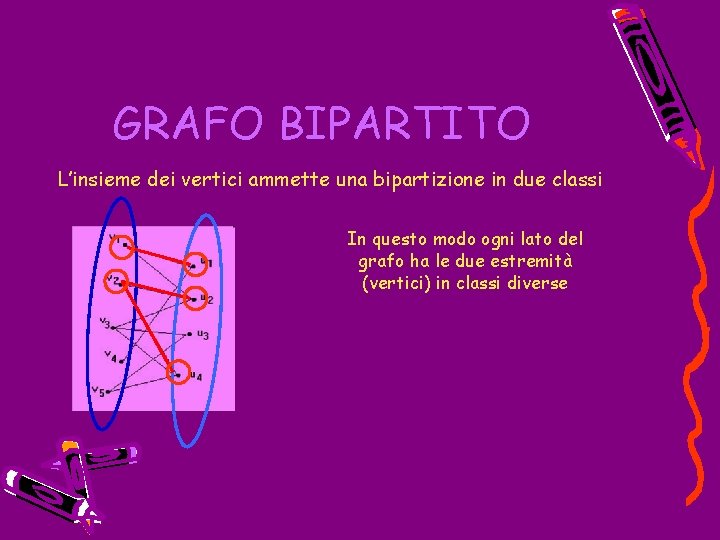
GRAFO BIPARTITO L’insieme dei vertici ammette una bipartizione in due classi In questo modo ogni lato del grafo ha le due estremità (vertici) in classi diverse

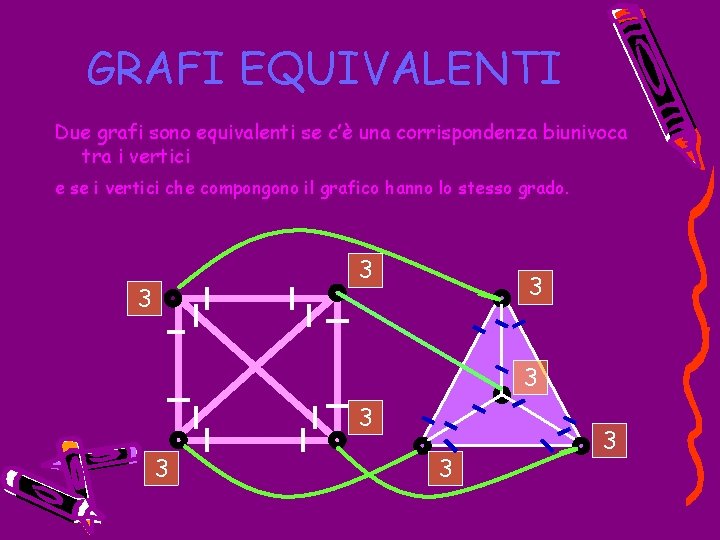
GRAFI EQUIVALENTI Due grafi sono equivalenti se c’è una corrispondenza biunivoca tra i vertici e se i vertici che compongono il grafico hanno lo stesso grado. 3 3 3 3

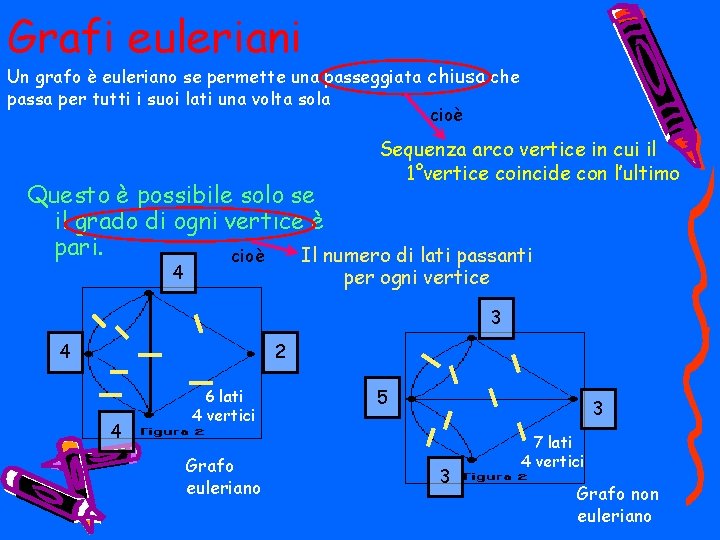
Grafi euleriani Un grafo è euleriano se permette una passeggiata chiusa che passa per tutti i suoi lati una volta sola cioè Sequenza arco vertice in cui il 1°vertice coincide con l’ultimo Questo è possibile solo se il grado di ogni vertice è pari. Il numero di lati passanti cioè 4 per ogni vertice 3 4 2 4 6 lati 4 vertici Grafo euleriano 5 3 3 7 lati 4 vertici Grafo non euleriano

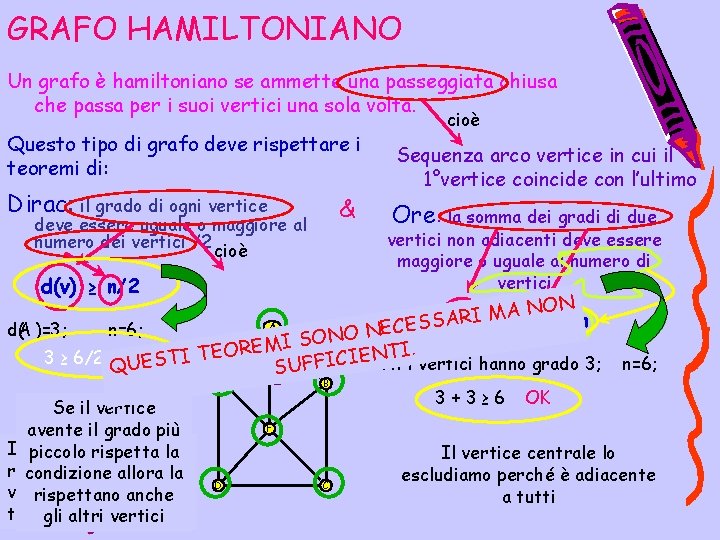
GRAFO HAMILTONIANO Un grafo è hamiltoniano se ammette una passeggiata chiusa che passa per i suoi vertici una sola volta. Questo tipo di grafo deve rispettare i teoremi di: Dirac: il grado di ogni vertice & deve essere uguale o maggiore al numero dei vertici /2 cioè Sequenza arco vertice in cui il 1°vertice coincide con l’ultimo Ore: la somma dei gradi di due vertici non adiacenti deve essere maggiore o uguale al numero di vertici d(v) ≥ n/2 ON N A M I R + d(v) ≥ n d(u) SSA A E C E n=6; d(A )=3 ; N SONO I M E R O TI. E N T E I I 3 ≥ 6/2 OK T C S I Tutti i vertici hanno grado 3; QUE SUFF E Se il vertice avente il grado più Il teorema è piccolo rispetta la rispettato daallora tutti ila condizione vertici perché anche hanno rispettano tuttigli grado 3 altri ≥vertici B 3+3≥ 6 n=6; OK F D C Il vertice centrale lo escludiamo perché è adiacente a tutti

Il problema della colorazione di una mappa In questo problema la teoria dei grafi trova una sua ulteriore applicazione. Per una miglior comprensione di una mappa geografica-politica si è solito utilizzare colori diversi per regioni adiacenti. Se hanno Per motivi di costi si preferisce almeno un ridurre al minimosegmento il numerodidi colori da utilizzare. confine in comune. In caso contrario, per esempio, per colorare la cartina dell’Italia avremo dovuto utilizzare 21 colori differenti Si è cercato, allora, il numero più piccolo di colori necessari alla comprensione della mappa

Ma quale è il numero minimo di colori? Molti studiosi hanno cercato di dare una risposta a questa domanda, che è giunta nel 1977 quando, con una complicata dimostrazione e l’aiuto di potenti computer , Appel e Haken scoprirono che un grafo planare è 4 -colorabile Così la cartina degli Stati Uniti è colorata con soli 4 colori invece che con 50 colori. v verde R rosso B blu G

Il teorema dei quattro colori può essere reso comprensibile grazie alla teoria dei grafi. Due vertici adiacenti non possono essere colorati allo stesso modo • Vertice del grafo= regione della mappa • Lato del grafo= confine che delimita 2 regioni adiacenti Appel e Haken scoprirono che ogni grafo piano è 4 -colorabile

L’esperienza “Lauree scientifiche” è stata molto interessante e significativa. Abbiamo seguito con interesse i corsi tenuti dai docenti universitari che ci hanno avvicinato alle materie scientifiche. Quest’esperienza ci ha permesso di crescere e di confrontarci con gli altri. Abbiamo lavorato, prima, singolarmente elaborando un nostro piccolo progetto che racchiudesse qualche nostra conoscenza e soprattutto ciò che, dalle varie lezioni all’università, abbiamo appreso. In una fase successiva, il confronto con altre persone della nostra stessa classe, ci ha arricchito notevolmente; inoltre il lavoro di gruppo è sempre piacevole e interessante. Nell’ultima fase del nostro lavoro abbiamo collaborato con ragazze di altre classi per mettere insieme i progetti realizzati singolarmente e il materiale che avevamo a disposizione, con opportuni approfondimenti. Questo confronto ci ha permesso di migliorare di volta in volta il progetto. Vorremo perciò ringraziare tutti i docenti universitari, ma in particolare la professoressa Polverino che ci ha fatto conoscere “la teoria dei grafi” che sopra abbiamo trattato. Ringraziamo anche i docenti del liceo scientifico “F. Quercia” che ci hanno accompagnati lungo il percorso e ci hanno dato la possibilità di partecipare al progetto.

Ringraziamo vivamente: La Prof. corso. Olga Polverino, della “UNINA 2” di Napoli, docente del Il Prof. Diamante Marotta, Dirigente Scientifico “F. Quercia” di Marcianise; I docenti cordinatori: Prof. ssa Scolastico Concetta Marino del e al Prof. Liceo Renzo Piccolo. Il nostro auspicio è che questa esperienza possa essere ripresa, e potenziata, nel prossimo anno scolatico. grazie DI MARSILIO CARMELA IV C MADONNA MARIADOMENICA IV A MARTONE RAFFAELLA IV C MIGLIORINI SONIA IV D