GRAFOS ESTRUCTURA DE DATOS INTRODUCCION Los grafos son

GRAFOS ESTRUCTURA DE DATOS

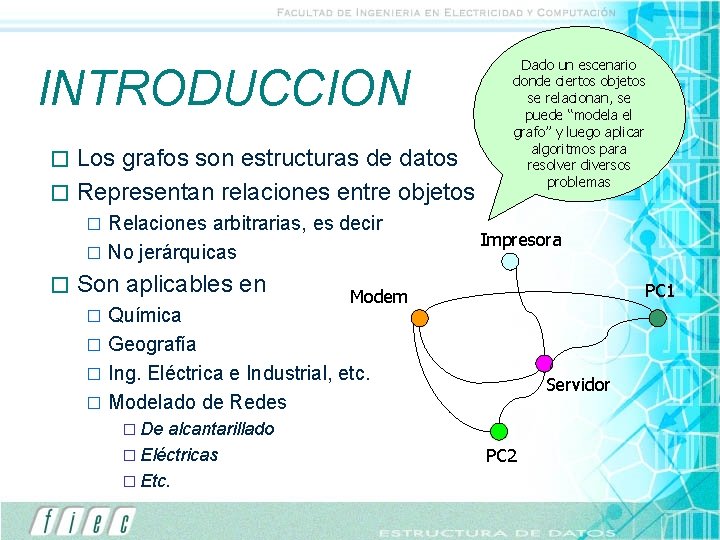
INTRODUCCION Los grafos son estructuras de datos � Representan relaciones entre objetos � Relaciones arbitrarias, es decir � No jerárquicas � � Son aplicables en Dado un escenario donde ciertos objetos se relacionan, se puede “modela el grafo” y luego aplicar algoritmos para resolver diversos problemas Impresora PC 1 Modem Química � Geografía � Ing. Eléctrica e Industrial, etc. � Modelado de Redes � alcantarillado � Eléctricas � Etc. Servidor � De PC 2

DEFINICION � Un � V, grafo G = (V, A) el conjunto de vértices o nodos � Representan � A, 4 5 los objetos el conjunto de arcos � Representan 1 7 las relaciones V = {1, 4, 5, 7, 9} A= {(1, 4), (5, 1), (7, 9), (7, 5), (4, 9), (4, 1), (1, 5), (9, 7), (5, 7), (9, 4)} 9

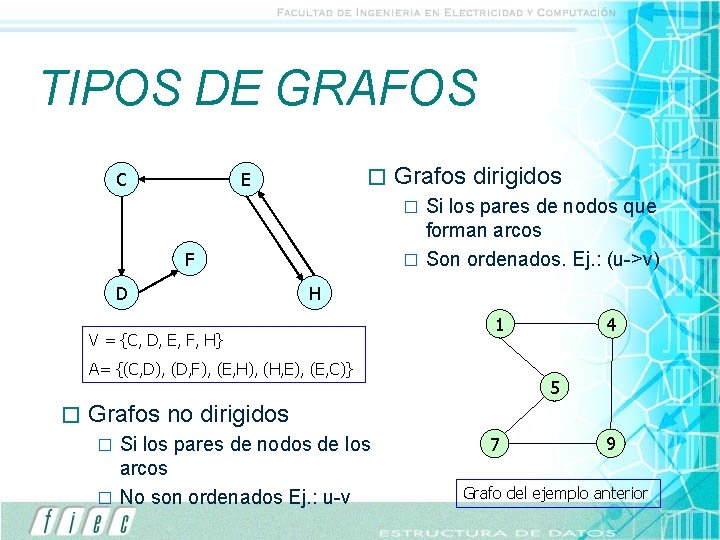
TIPOS DE GRAFOS C � E Grafos dirigidos Si los pares de nodos que forman arcos � Son ordenados. Ej. : (u->v) � F D H V = {C, D, E, F, H} 1 A= {(C, D), (D, F), (E, H), (H, E), (E, C)} � 4 5 Grafos no dirigidos Si los pares de nodos de los arcos � No son ordenados Ej. : u-v � 7 9 Grafo del ejemplo anterior

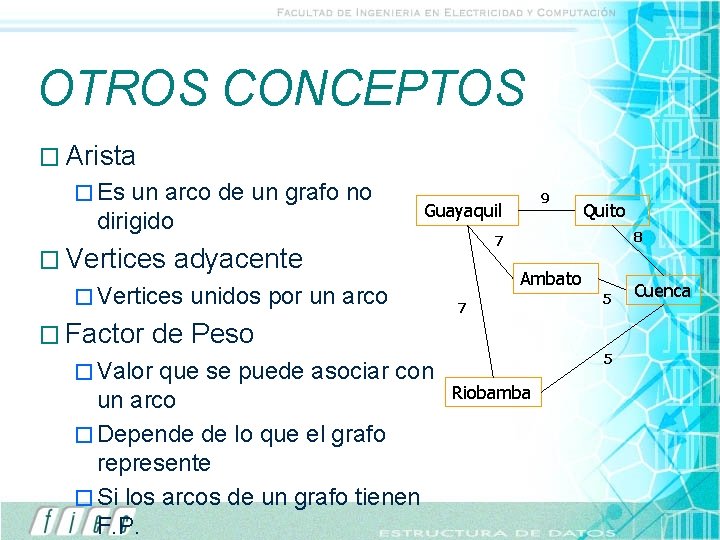
OTROS CONCEPTOS � Arista � Es un arco de un grafo no dirigido � Vertices � Factor Guayaquil unidos por un arco Quito 8 7 adyacente � Vertices 9 Ambato 7 5 de Peso � Valor que se puede asociar con un arco � Depende de lo que el grafo represente � Si los arcos de un grafo tienen F. P. 5 Riobamba Cuenca

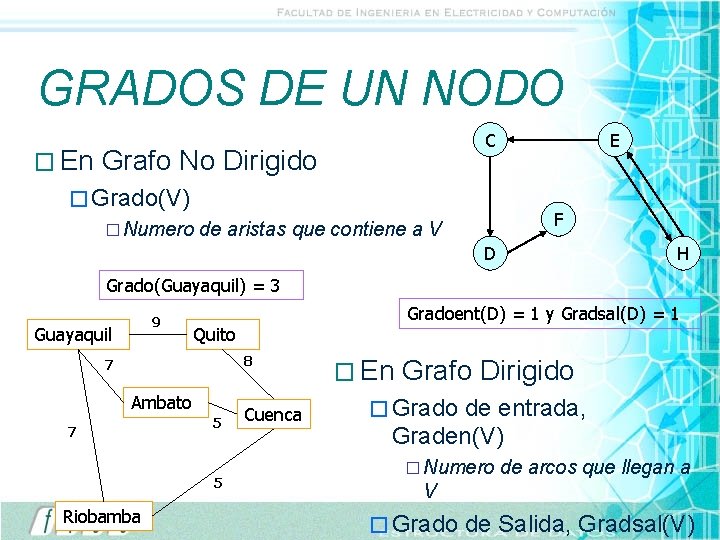
GRADOS DE UN NODO � En C Grafo No Dirigido � Grado(V) � Numero E F de aristas que contiene a V D H Grado(Guayaquil) = 3 9 Guayaquil Gradoent(D) = 1 y Gradsal(D) = 1 Quito 8 7 Ambato 7 5 5 Riobamba Cuenca � En Grafo Dirigido � Grado de entrada, Graden(V) � Numero de arcos que llegan a V � Grado de Salida, Gradsal(V)

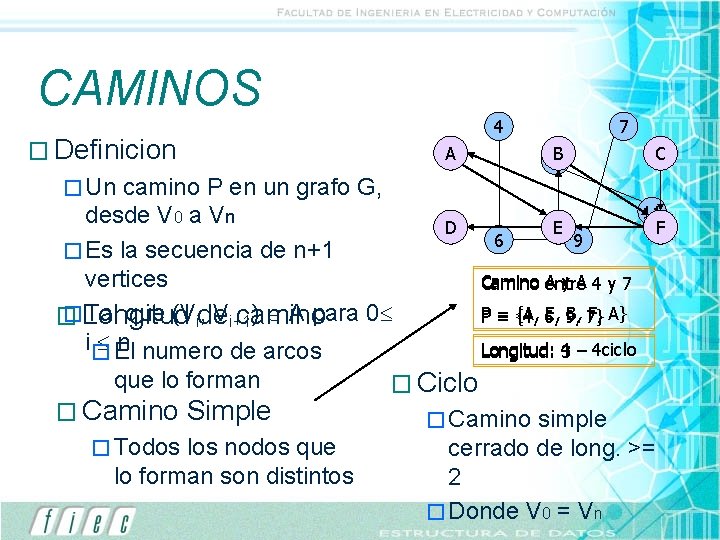
CAMINOS 4 � Definicion A camino P en un grafo G, desde V 0 a Vn � Es la secuencia de n+1 vertices �Longitud Tal que (Vide , Vi+1 ) A para 0 � camino i� El n numero de arcos 7 B 10 C E 11 F � Un que lo forman � Camino � Todos Simple los nodos que lo forman son distintos D 6 9 Camino A y. A 4 y 7 entre P = {A, E, 9, B, 7} F, A} {4, 6, Longitud: 4 3 – 4 ciclo � Camino simple cerrado de long. >= 2 � Donde V 0 = Vn

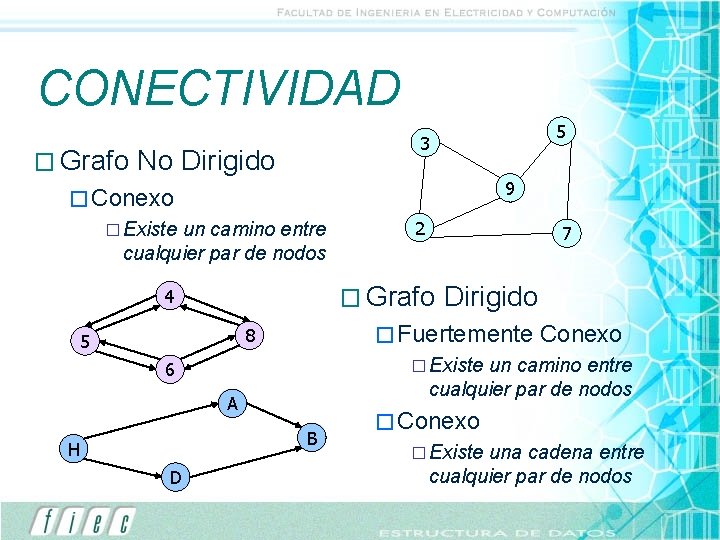
CONECTIVIDAD � Grafo 5 3 No Dirigido 9 � Conexo � Existe un camino entre cualquier par de nodos Dirigido � Fuertemente 8 5 Conexo � Existe un camino entre cualquier par de nodos 6 A B D 7 � Grafo 4 H 2 � Conexo � Existe una cadena entre cualquier par de nodos

TDA GRAFO � Datos � Vertices y � Arcos(relacion entre vertices) � Operaciones � void Añadir. Vertice(Grafo G, Vertice V) � Añadir un nuevo vertice � void Borrar. Vertice(Grafo G, � Eliminar un vertice existente � void Union(Grafo � Unir dos vertices Generico clave) G, Vertice V 1, Vertice V 2) � Void Borrar. Arco(Grafo G, Vertice V 1, Vertice V 2) � Eliminar � bool un Arco Es. Adyacente(Grafo G, Vertice V 1, Vertice V 2)

REPRESENTACION � Dos posibles representaciones �Estatica: �Los Matriz de Adyacencia vertices se representan por indices(0…n) �Las relaciones de los vertices se almacenan en una Matriz �Dinamica: �Los Lista de Adyacencia vertices forman una lista �Cada vertice tiene una lista para representar sus relaciones(arcos)

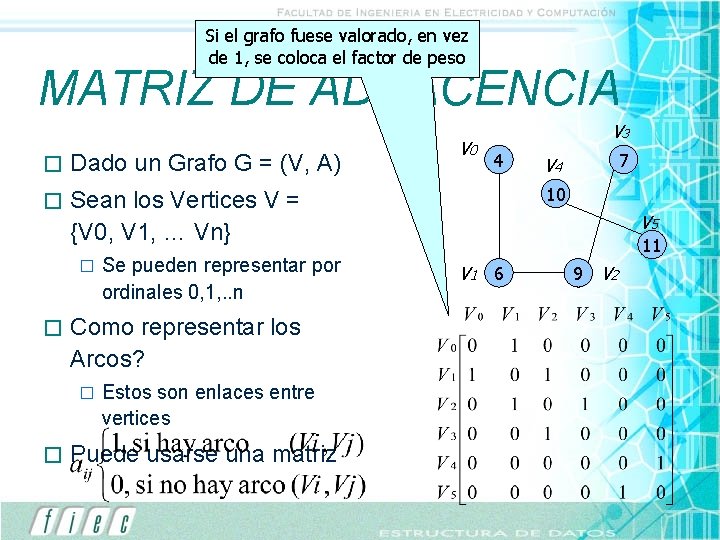
Si el grafo fuese valorado, en vez de 1, se coloca el factor de peso MATRIZ DE ADYACENCIA � Dado un Grafo G = (V, A) � Sean los Vertices V = {V 0, V 1, … Vn} � � Como representar los Arcos? � � Se pueden representar por ordinales 0, 1, . . n Estos son enlaces entre vertices Puede usarse una matriz V 0 V 3 4 7 V 4 10 V 5 11 V 1 6 9 V 2

EL TIPO DE DATO � Los Vertices �Se definen en un Arreglo � Los #define MAX 20 typedef int [MAX] Matriz. Ady; typdef Generico[MAX] Vertices; typedef struct Grafo{ Arcos Vertices V; Matriz. Ady A; �Se definen en una Matriz int nvertices; bool Dirigido; };

UNIR VERTICE void Union(Grafo G, int v 1, int v 2){ } G->A[v 1][v 2] = 1; if(!G->dirigido) G->A[v 2][v 1] = 1;

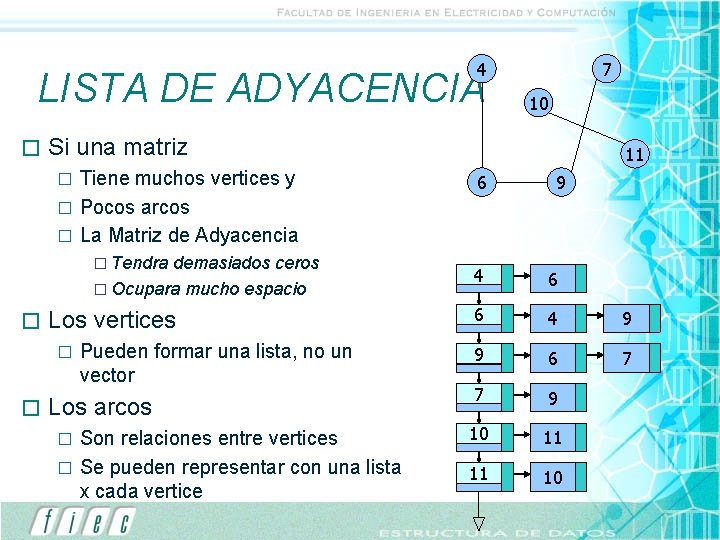
4 LISTA DE ADYACENCIA � Tiene muchos vertices y � Pocos arcos � La Matriz de Adyacencia � Tendra demasiados ceros � Ocupara mucho espacio Los vertices � � 10 Si una matriz � � 7 Pueden formar una lista, no un vector Los arcos Son relaciones entre vertices � Se pueden representar con una lista x cada vertice � 11 6 9 4 6 6 4 9 9 6 7 7 9 10 11 11 10

EL TIPO DE DATO � Cada vertice tiene typedef struct Vertice{ � Contenido Generico contenido; � Siguiente LSE *LA; � Una lista de adyacencia � Cada nodo en la lista de adyacencia � Peso }; typedef Vertice *Arco; typedef struct Grafo{ del arco � Siguiente }; � Una referencia al vertice(arco) LSE LVertices; bool dirigido;

ALGUNAS IMPLEMENTACIONES void Union(Grafo G, Vertice V 1, Vertice V 2){ LSE_Insertar. Nodo. Fin(V 1 ->Larcos, LSE_Crear. Nodo(V 2)); if(!G->dirigido) LSE_Insertar. Nodo. Fin(V 2 ->Larcos, LSE_Crear. Nodo(V 1); }

EJERCICIO � Complete la implementacion de las operaciones del grafo con lista de adyacencia

RECORRIDOS DEL GRAFO � Se busca �Visitar todos los nodos posibles �Desde un vertice de partida D �Cualquiera � Existe �En dos posibles recorridos Anchura y �En Profundidad

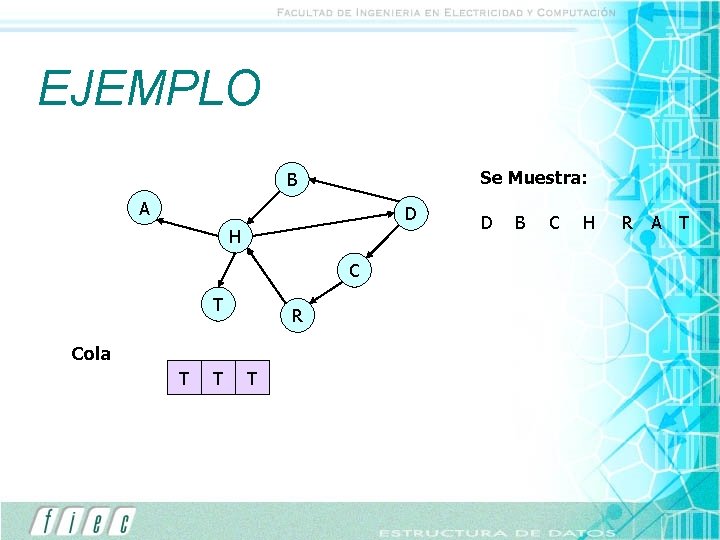
RECORRIDO EN ANCHURA � Encolar vertice de partida � Marcarlo como “visitado” � Mientras la cola no este vacia � Desencolar vertice W � Mostrarlo � Marcar como visitados � Los vertices adyacentes de W � Que no hayan sido ya visitados � Encolarlos

EJEMPLO Se Muestra: B A D H C T R Cola D H R C A B T H R C A T T D B C H R A T

IMPLEMENTACION LSE *Recorrer. En. Anchura(Grafo G, Vertice V){ LSE *L; LSE_nodo *sacado, *parco; Vertice *vsacado, *varco; Cola Q; L = malloc(sizeof(LSE)); LSE_Inicializar(L); Cola_Inicializar(&Q); V. visitado = TRUE; En. Colar(&Q, LSE_Nodo. Crear(&V)); while(!Cola_Esta. Vacia(Q)){ sacado = Des. En. Colar(&Q); vsacado = Generico_Obtener. Vertice(sacado->G); LSE_Insertar. Nodo. Fin(L, LSE_Nodo. Crear(vsacado)); for(parco = vsacado->LArcos->header; parco!=NULL; parco = parco->sig){ varco = Generico_Obtener. Vertice(parco->G); if(!varco->visitado){ varco->visitado = TRUE; En. Colar(&Q, LSE_Nodo. Crear(varco)); } } } return L; }

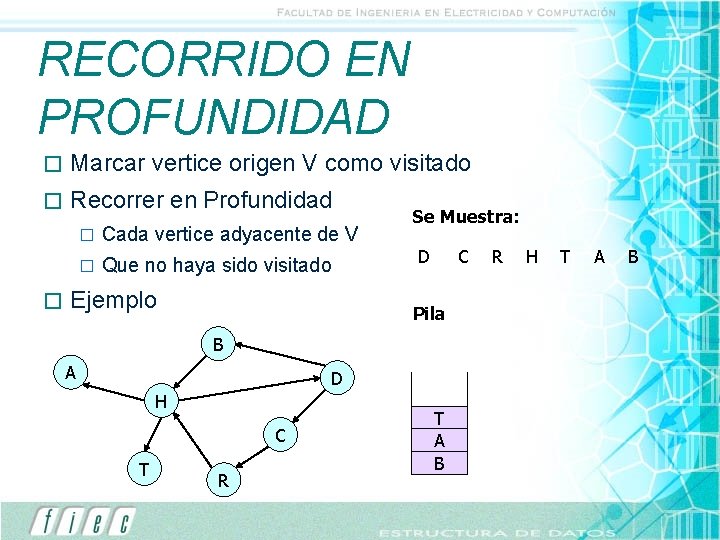
RECORRIDO EN PROFUNDIDAD � Marcar vertice origen V como visitado � Recorrer en Profundidad � � Cada vertice adyacente de V � Que no haya sido visitado Ejemplo Se Muestra: D C Pila B A D H C T R T H R C A D B R H T A B

EJERCICIO Escriba la implementacion del recorrido en profundidad de un grafo a partir de un vertice inicial