Classification Ex 90 marks A 80 marks 90

Classification • Ex 90<= marks A 80<= marks 90 B 70<= marks < 80 C 60<= marks < 70 D marks<60 10/2/2020 F Data Mining -By Dr. S. C. Shirwaikar 1

Classification • predicts categorical class labels (discrete or nominal) • classifies data (constructs a model) based on the training set and the values (class labels) in a classifying attribute and uses it in classifying new data Defn: Given a Database D={t 1, t 2, …tn} of tuples and a set C={C 1, C 2, …Cm}, the classification problem is to define a mapping f: D C where each ti is assigned to one class Cj. Second Problem Overfitting 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 2

Classification Three basic methods used to solve classification problems • Specifying boundaries • Using probability distributions p(ti/Cj) • Using posterior probabilities p(Cj/ti) 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 3

Typical applications • Credit approval-applicant as good or poor credit risk • Target marketing-profile of a good customer • Medical diagnosis- Develop a profile of stroke victims • Fraud detection -Determine a credit card purchase is fraudulent Classification is a two-step process Classifier is built from a data set- learning step The training data set contains tuples having attributes one of which is a class label attribute 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 4

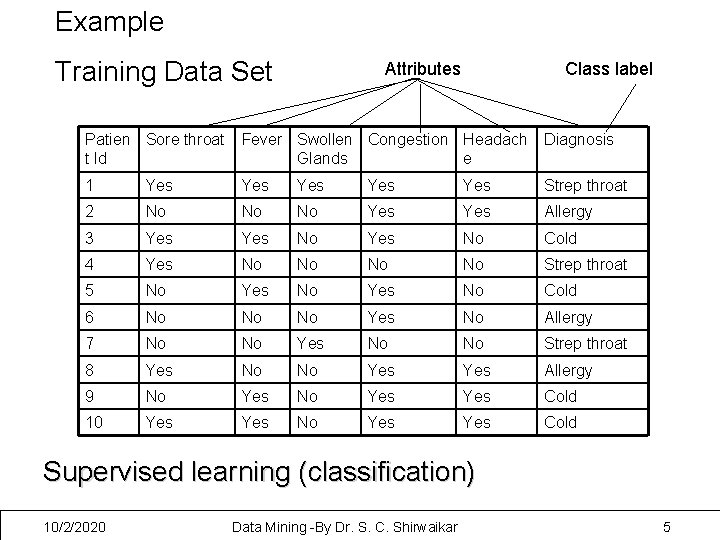
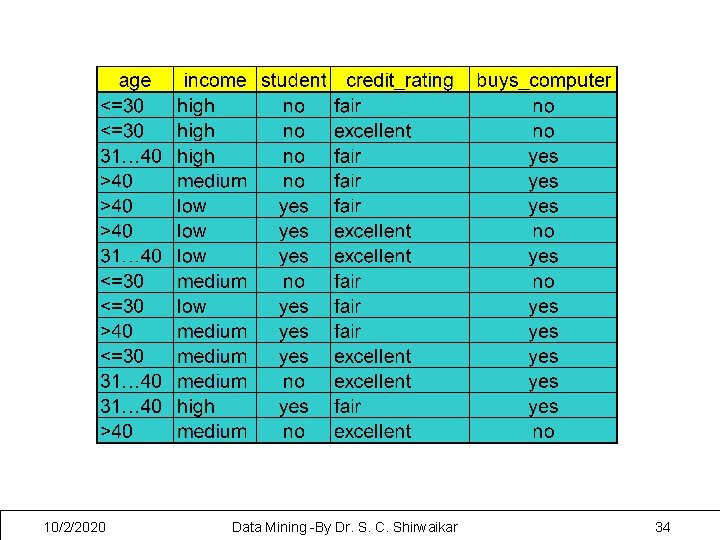
Example Training Data Set Attributes Class label Patien Sore throat t Id Fever Swollen Congestion Headach Glands e Diagnosis 1 Yes Yes Yes Strep throat 2 No No No Yes Allergy 3 Yes No Cold 4 Yes No No Strep throat 5 No Yes No Cold 6 No No No Yes No Allergy 7 No No Yes No No Strep throat 8 Yes No No Yes Allergy 9 No Yes Yes Cold 10 Yes No Yes Cold Supervised learning (classification) 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 5

Since class label is provided it is known as supervised learning 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 6

Model construction: • Describing a set of predetermined classes • Each tuple/sample is assumed to belong to a predefined class, as determined by the class label attribute • The set of tuples used for model construction is training set • The model is represented as classification rules, decision trees, or mathematical formulae Model usage: • for classifying future or unknown objects • Estimate accuracy of the model The known label of test sample is compared with the classified result from the model • Accuracy rate is the percentage of test set samples that are correctly classified by the model • Test set is independent of training set, otherwise over-fitting will occur • If the accuracy is acceptable, use the model to classify data tuples whose class labels are not known 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 7

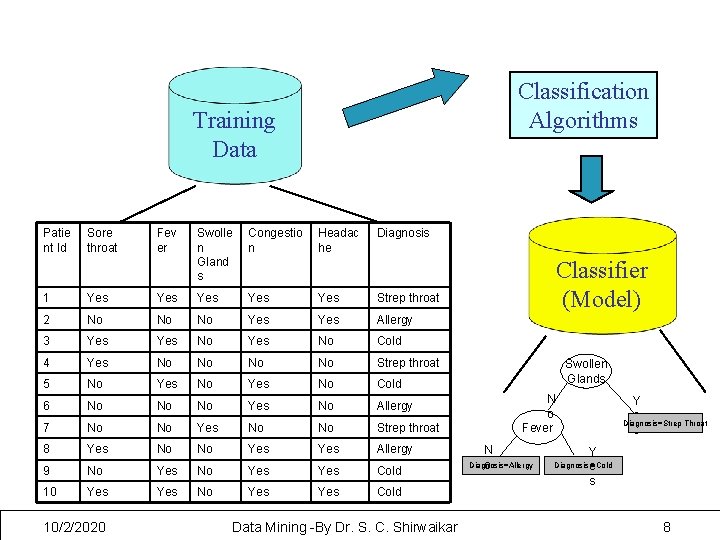
Classification Algorithms Training Data Patie nt Id Sore throat Fev er Swolle n Gland s Congestio n Headac he Diagnosis 1 Yes Yes Yes Strep throat 2 No No No Yes Allergy 3 Yes No Cold 4 Yes No No Strep throat 5 No Yes No Cold 6 No No No Yes No Allergy 7 No No Yes No No Strep throat 8 Yes No No Yes Allergy 9 No Yes Yes Cold 10 Yes No Yes Cold 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar Classifier (Model) Swollen Glands N o Fever N Diagnosis=Allergy o Y e Diagnosis=Strep Throat s Y Diagnosis e =Cold s 8

Preparing data for classification • Data cleaning – Preprocess data in order to reduce noise and handle missing value Ignore missing data Assume a value for the missing data. This meas that the value of missing data is taken to be a specific value all of its own. 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 9

• Relevance analysis (feature selection) – Remove the irrelevant or redundant attributes – Redundant attributes may be able to be detected by correlation analysis – Improves classification efficiency and scalability • Data transformation – Generalize and/or normalize data -- Data Reduction 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 10

Choosing Classification Algorithms • Algorithm categorization • Distance based • Statistical • Decision Tree Based • Neural network • Rule based • Classification categorization • Specifying boundaries-divides input space into regions • Probabilistic- determine probability for each class and assign tuple to the class with highest probability 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 11

Measuring Performance • Performance of classification algorithm is by evaluating accuracy of the classification • Computational costs -Space and time requirements • Scalability-efficient even for large databases • Robustness-ability to make correct classification in the presence of noisy data • Overfitting problem- the classification fits the training data exactly but may not be applicable to a broader population of data • Interpretability- insight provided by classifier 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 12

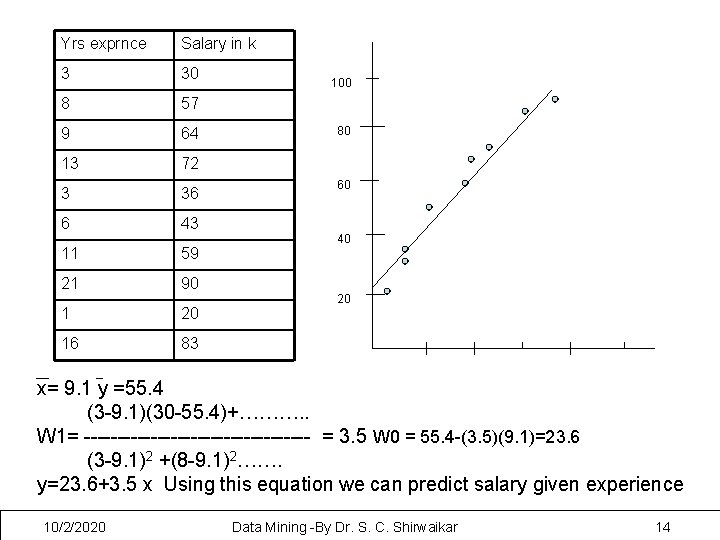
Statistical-based algorithms Straight line regression analysis involves a response variable y and a single predictor variable x and models y is a linear function of x y = w 0 + w 1 x where w 0 (y-intercept) and w 1 (slope) are regression coefficients These coefficients can be solved by the method of least squares which estimates the best fitting straight line D be the training data set containing n data points (x 1, y 1), (x 2, y 2)…(xn, yn), regression coefficients can be estimated as ∑ (xi- x) (yi –y) w 1 = ------------ w 0 = y – w 1 x ∑ (xi- x)2 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 13

Yrs exprnce Salary in k 3 30 8 57 9 64 13 72 3 36 6 43 11 59 21 90 1 20 16 83 100 80 60 40 20 x= 9. 1 y =55. 4 (3 -9. 1)(30 -55. 4)+………. . W 1= ----------------- = 3. 5 W 0 = 55. 4 -(3. 5)(9. 1)=23. 6 (3 -9. 1)2 +(8 -9. 1)2……. y=23. 6+3. 5 x Using this equation we can predict salary given experience 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 14

Multiple Linear regression It is an extension of Straight line regression analysis so as to involve more than one predictor variable It allows response variable y to be modeled as a linear function of n predictor variables or attributes describing a tuple x as (x 1, x 2, …xn) y = w 0 + w 1 x 1 +w 2 x 2+w 3 x 3+…. . wnxn The method of least squares can be extended to solve for w 0, w 1 etc. the equations are much more complex and can be solved by using statistical software packages 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 15

The linear model gets affected by the presence of noise or outliers (extreme, exceptional values) Nonlinear regression • Some nonlinear models can be modeled by a polynomial function • A polynomial regression model can be transformed into linear regression model. For example, y = w 0 + w 1 x + w 2 x 2 + w 3 x 3 convertible to linear with new variables: x 2 = x 2, x 3= x 3 y = w 0 + w 1 x + w 2 x 2 + w 3 x 3 • Some models are intractable nonlinear (e. g. , sum of exponential terms) – possible to obtain least square estimates through extensive calculation on more complex formulae 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 16

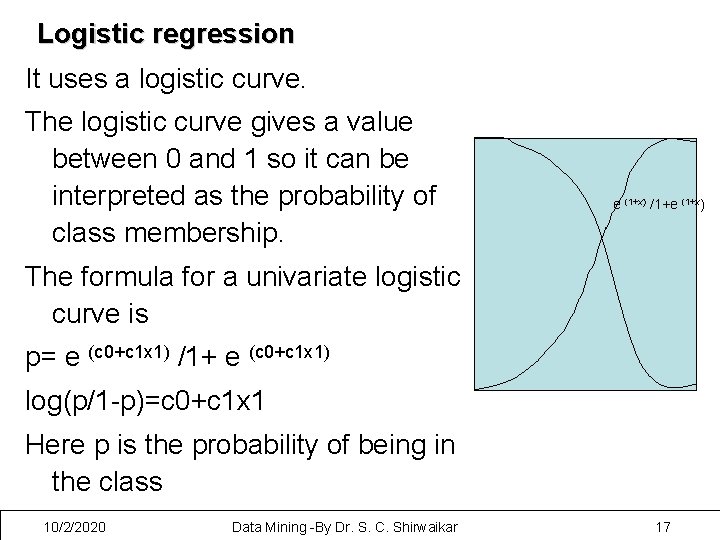
Logistic regression It uses a logistic curve. The logistic curve gives a value between 0 and 1 so it can be interpreted as the probability of class membership. e (1+x) /1+e (1+x) The formula for a univariate logistic curve is p= e (c 0+c 1 x 1) /1+ e (c 0+c 1 x 1) log(p/1 -p)=c 0+c 1 x 1 Here p is the probability of being in the class 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 17

Bayesian Classification: It is based on Bayes’ Theorem of conditional probability. It is a statistical classifier: performs probabilistic prediction, i. e. , predicts class membership probabilities A simple Bayesian classifier, naïve Bayesian classifier, assumes that different attribute values are independent which simplifies computational process It has comparable performance with decision tree and selected neural network classifiers 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 18

Let X be a data tuple (“evidence”): described by values of its n attributes Let H be a hypothesis that X belongs to class C Classification is to determine P(H|X), the probability that the hypothesis holds given the observed data sample X Probability that X belongs to class C having known the attribute description of X Given that X is 31. . 40 and medium income , X will buy computer P(H) (prior probability H ), the initial probability E. g. , X will buy computer, regardless of age, income, … 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 19

Let X be a data tuple (“evidence”): described by values of its n attributes Let H be a hypothesis that X belongs to class C Classification is to determine P(H|X), the probability that the hypothesis holds given the observed data sample X Probability that X belongs to class C having known the attribute description of X Given that X is 31. . 40 and medium income , X will buy computer P(H) (prior probability H ), the initial probability E. g. , X will buy computer, regardless of age, income, … 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 20

P(H/X) (posteriori probability of H ), the probability of H when attributes of X are known P(X): (prior probability of X) It is probability that sample data is in observed range Ex It is probability that person is in the range 31. . 40 and medium income- evidence P(X/H) (posteriori probability of X) -likelihood E. g. , Given that X will buy computer, the prob. that X is 31. . 40, medium income Baye’s theorem relates all these probabilities P(H/X)= P(X/H) P(X) Posteriori= Likelihood x priori / evidence 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 21

Let D be a training set of tuples and their associated class labels, and each tuple is represented by an n-D attribute vector X = (x 1, x 2, …, Xn) Suppose there are m classes C 1, C 2, …, Cm. Classification is to derive the maximum posteriori, i. e. , the maximal P(Ci|X) This can be derived from Bayes’ theorem P(Ci/X)= P(X/Ci) P(X) Since P(X) is constant for all classes, only P(X/Ci)P(Ci) needs to be maximized 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 22

If class prior probabilities are not known, it can be assumed that all classes are equally likely P(C 1)=P(C 2) =………………. . =P(Cn) Reduced to maximizing P(X/Ci) If data set has many attributes, it will be computationally expensive to compute P(X/Ci) To reduce computation, assumption of class conditional independence is made Attributes are conditionally independent P(X/Ci)= P(x 1/Ci)x. P(x 2/Ci)x………………x P(xn/Ci) 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 23

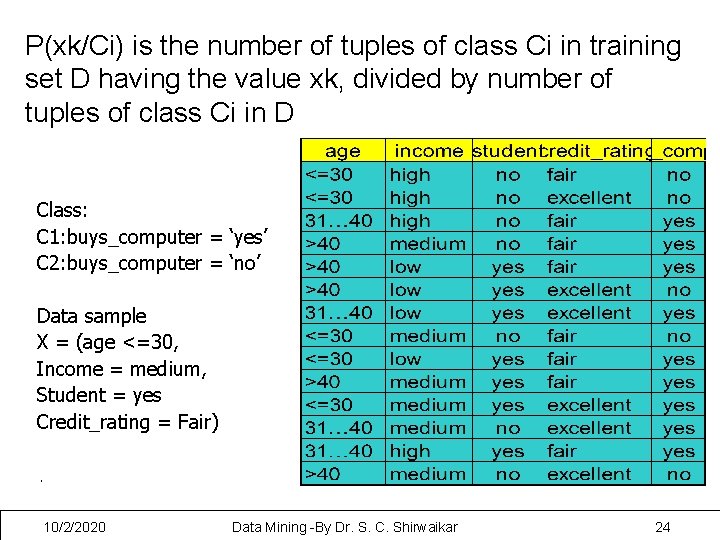
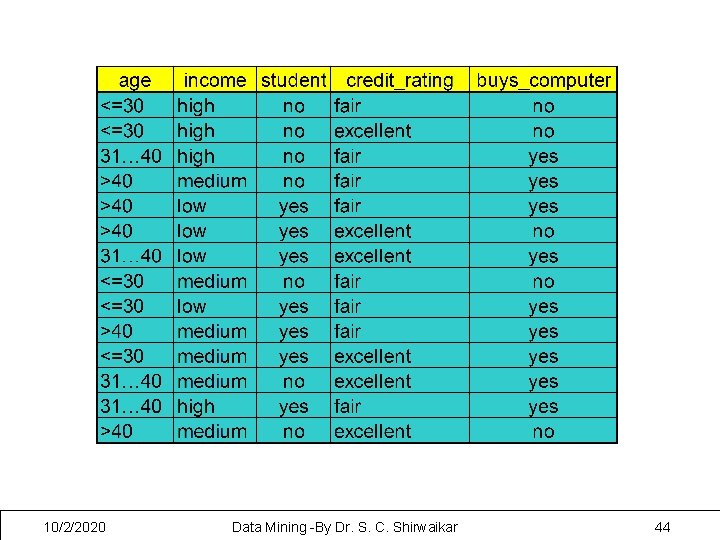
P(xk/Ci) is the number of tuples of class Ci in training set D having the value xk, divided by number of tuples of class Ci in D Class: C 1: buys_computer = ‘yes’ C 2: buys_computer = ‘no’ Data sample X = (age <=30, Income = medium, Student = yes Credit_rating = Fair) 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 24

• P(Ci): P(buys_computer = “yes”) = 9/14 = 0. 643 P(buys_computer = “no”) = 5/14= 0. 357 • Compute P(X|Ci) for each class P(age = “<=30” | buys_computer = “yes”) = 2/9 = 0. 222 P(age = “<= 30” | buys_computer = “no”) = 3/5 = 0. 6 P(income = “medium” | buys_computer = “yes”) = 4/9 = 0. 444 P(income = “medium” | buys_computer = “no”) = 2/5 = 0. 4 P(student = “yes” | buys_computer = “yes) = 6/9 = 0. 667 P(student = “yes” | buys_computer = “no”) = 1/5 = 0. 2 P(credit_rating = “fair” | buys_computer = “yes”) = 6/9 = 0. 667 P(credit_rating = “fair” | buys_computer = “no”) = 2/5 = 0. 4 • X = (age <= 30 , income = medium, student = yes, credit_rating = fair) P(X|Ci) : P(X|buys_computer = “yes”) = 0. 222 x 0. 444 x 0. 667 = 0. 044 P(X|buys_computer = “no”) = 0. 6 x 0. 4 x 0. 2 x 0. 4 = 0. 019 P(X|Ci)*P(Ci) : P(X|buys_computer = “yes”) * P(buys_computer = “yes”) = 0. 028 P(X|buys_computer = “no”) * P(buys_computer = “no”) = 0. 007 Therefore, X belongs to class (“buys_computer = yes”) 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 25

Zero-probability problem Naïve Bayesian prediction requires each conditional prob. to be non-zero. Otherwise, the predicted prob. will be zero irrespective of all other probabilities Ex. Suppose a dataset with 1000 tuples, income=low (0), income= medium (990), and income = high (10), Use Laplacian correction (or Laplacian estimator) Adding 1 to each case Prob(income = low) = 1/1003 Prob(income = medium) = 991/1003 Prob(income = high) = 11/1003 The “corrected” prob. estimates are close to their “uncorrected” counterparts and the problem of zero probability is solved 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 26

Advantages • Easy to implement • Only one scan of training data is required • Good results obtained in most of the cases • Can easily handle missing values Disadvantages • Assumption: class conditional independence, therefore loss of accuracy • Practically, dependencies exist among variables E. g. , hospitals: patients: Profile: age, family history, etc. Symptoms: fever, cough etc. , Disease: lung cancer, diabetes, etc. Dependencies among these cannot be modeled by Naïve Bayesian Classifier Bayesian Belief Networks 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 27

Distance-based algorithms Each tuple is assigned to class to which it is most similar Each class is represented as a tuple The representative for each class is the centre or centroid Each tuple ti is assigned to class Cj such that sim(ti, Cj) >sim(ti, Cl) for all Cl such that Cl ≠Cj Each tuple must be compared to the center for a class and there are fixed number of classes. The complexity depends on the number of classes K Nearest Neighbors is a distance based algorithm i. e a lazy learning algorithm. Simply stores training data (or only does minor processing) and waits until it is given a test tuple 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 28

Distance-based algorithms Similarity or distance measures may be used to identify the alikeness of different items in the database The similarity between two tuples ti and tj sim(ti, tj) , in a database D is a mapping from Dx. D to the range [0, 1] Characteristics of a good similarity measure 1. sim(ti, ti)=1 for all ti 2. sim(ti, tj)=0 if ti and tj are not alike at all 3. sim(ti, tj) < sim(ti, tk) if ti is more like tk than it is like tj 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 29

Dice: sim(ti, tj) = ∑ tik tjk ∑ tik 2 + ∑tjk 2 Jaccard : sim(ti, tj) = Cosine : sim(ti, tj) = ∑ tik tjk ∑ tik 2 +∑tjk 2 - ∑ tik tjk ∑ tik 2 ∑tjk 2 Overlap : sim(ti, tj) = ∑ tik tjk min (∑ tik 2, ∑tjk 2) Distance or dissimilarity measures are often used instead of similarity measures-usually distance measures Euclidean : dis(ti, tj) = ∑ (tih-tjh)2 Manhattan : dis(ti, tj) = ∑ | tih-tik| 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 30

The k-Nearest neighbor algorithm • K closet neighbors in the training set to the given tuple are to be determined • The nearest neighbor are defined in terms of Euclidean distance, dist(X 1, X 2) • The new item is then placed in the class that contains the most items from this set k of closest items • The value of k can be determined experimentally. Starting with k=1, a test set is used to estimate the error rate of the classifier. The k value that gives minimum error rate can be selected • k-NN for real-valued prediction for a given unknown tuple returns the mean values of the k nearest neighbors 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 31

The k-Nearest neighbor algorithm • Distance-weighted nearest neighbor algorithm gives greater weight to closer neighbors • Robust to noisy data by averaging k-nearest neighbors • The complexity is O(d), d is the size of training set, can be reduced to O(logd) by storing training set in search trees, can be O(1) by using parallelism 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 32

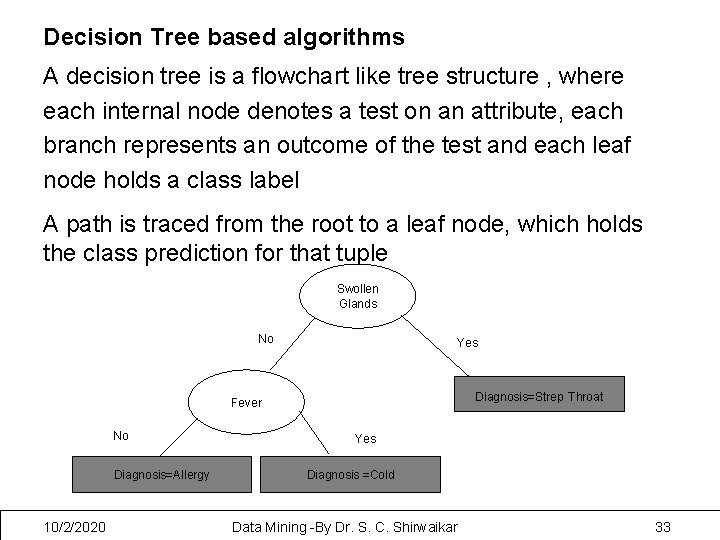
Decision Tree based algorithms A decision tree is a flowchart like tree structure , where each internal node denotes a test on an attribute, each branch represents an outcome of the test and each leaf node holds a class label A path is traced from the root to a leaf node, which holds the class prediction for that tuple Swollen Glands No Yes Diagnosis=Strep Throat Fever No Diagnosis=Allergy 10/2/2020 Yes Diagnosis =Cold Data Mining -By Dr. S. C. Shirwaikar 33

10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 34

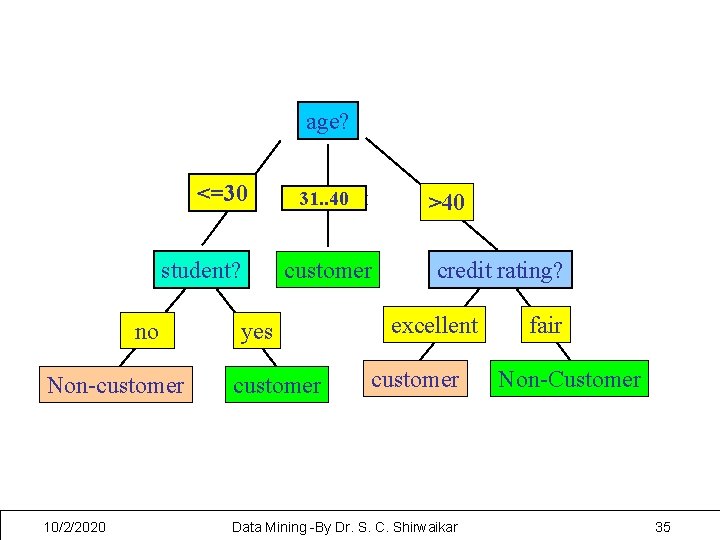
age? <=30 student? no 31. . 40 overcast >40 customer yes credit rating? excellent customer Non-customer 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar fair Non-Customer 35

Algorithm Generate_decision_tree(D, attribute_list) Create a Node N If tuples in D are in the same class C then return N as leaf node labeled with class C If attribute list is empty then return N as a leaf node labeled with the majority class in D Apply attribute selection method D to get the best splitting attribute and label the node accordingly Split the node depending on attribute domain For each split Let Dj be the set of data tuples in D satisfying outcome j If Dj is empty then attach a leaf labeled with majotrity class in D Else give a recursive call to Generate _decsion tree for the new node 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 36

Decision_Tree induction: Construct a DT using training data For each ti € D, apply the DT to determine it’s class. Advantages: 1. Easy to use and efficient 2. Rules can br generated that are easy to interpret and understand. 3. They scale well for large databases because the tree size is independent of database size. 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 37

Input. D //training data Output: T //Decision Tree DTBuild algorithm: T= ø Determine best splitting criterion: T= Create root node and label with splitting attribute; T= Add arc to root node for each split predicate and label; for each arc do D = Database created by applying splitting predicate to D; If stopping point reached for this path, then T’= Create leaf node and label with appropriate class; else T’=DTBuild(D); T’= Add T’ to arc; 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 38

Disadvantages: 1. They do not easily handle continuous data 2. These attribute domain must be divided into categories to be handled. 3. 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 39

Issues faced by DT algorithms • Choosing splitting attributes -best splitting criterion is when all tuples in the partition belong to the same class(pure). Some attributes are better than other. Choice of attribute should be such that it minimizes the expected number of tests needed to classify a given tuple and guarantees a simple tree structure • Ordering of splitting attributes – The order in which the attributes are chosen is important • The attributes are ranked based on some attribute selection measure. The best score attribute is chosen as splitting attribute • Splits- number of splits depends on the domain of the attribute • Tree structure- a balanced tree with the fewest levels is desirable 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 40

• Stopping criteria – The creation of the tree stops when the training data is perfectly classified. Stopping earlier can prevent overfitting and generation of large trees • Training data –Training data set can give rise to overfitting problem • Pruning- Once a tree is constructed , some modifications to the tree might not be specific enough to work properly with more general data. ID 3(Iterative Dichotomiser) ID 3 technique of building a decision tree is based on information theory and attempts to minimize excepted number of comparisons Like in “Twenty question Game” ask questions that provide the most information 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 41

Entropy is used to measure the amount of uncertainity or surprise in a set of data When all data in a set belongs to the same class there is no uncertainity – entropy is zero The objective of decision tree classification is to iteratively partition the given data set into subsets where all elements in each final subset belong to the same class-pure partition Defn : Given a data set D and probabilities p 1, p 2, …pn where ∑ pi=1, pi is the probability that an arbitrary tuple in D belongs to Class Ci, entropy or expected information neededd to classify a tuple in D is defined as H(D)= ∑ pi (log(1/pi)) = - ∑ pi log(pi) 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 42

If selection of an attribute A does not result into pure partitions then additional information required in order to arrive at exact classification is measured as info. A(D) = ∑|Dj|/|D| x Info(Dj) The term |Dj|/|D| acts as the weight of the jth partition Information gained by branching on attribute A Gain(A)=Info(D)-Info. A(D) The difference between the original information requirement based on just the proportion of classes and the new requirement obtained after partitioning on A The smaller the expected information , the greater is the purity of the partitions Select the attribute with the highest information gain 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 43

10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 44

H(D) = Info(D) = -9/14 log(9/14) – 5/14 log (5/14) =0. 940 If the tuples are classified according to attribute age The Expected information required for further classification after partitioning on Attribute age Info age(d) = 5/14 x( -2/5 log(2/5)-3/5 log(3/5)) + 4/14 x( -4/4 log(4/4)-0/4 log(0/4)) + 5/14 x( -3/5 log(3/5)-2/5 log(2/5)) = 0. 694 bits Hence gain in information Gain(age) = Info(d) – Infoage(D) = 0. 940 -0. 694=0. 246 Similarly gains for other attributes can be calculated Gain(Income) =0. 029 Gain(student)=0. 151 and Gain(credit_rating)=0. 048 Hence attribute age is chosen as the splitting attribute 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 45

C 4. 5 is a successor of ID 3 It improves ID 3 in the following ways Missing data- instead of ignoring missing data , the value is predicted based on what is known about the attributes of other records Continuous data- discretized by dividing data into ranges Pruning- with subtree replacement , a subtree is replaced by a leaf node, if this replacement results in an error rate close to that of the original tree –bottom up -With Subtree raising, a subtree is replaced by its most used subtree. Subtree is raised to a higher location depending on increase in error rate 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 46

Rules - generates both decision tree and the rules set. . Some methods are used to simplify rules such as replacing rule by a simpler version Splitting – The ID 3 approach favors attributes with many divisions and thus may lead to overfitting. An improvement can be made by taking into account the cardinality of each division. The Gain. Ratio is used opposed to Gain. Ratio(D, S)= Gain(D, S) / H(|Di|/|D|) C 4. 5 uses the largest Gainratio that ensures larger than average Information gain For the attribute Income H(|Di|/|D|) = -4/14 log(4/14) -6/14 log(6/14) – 4/14 log(4/14) = 0. 926 Gainratio= Gain(Income)/0. 926=0. 029/0. 926=0. 031 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 47

CART (Classification and regression trees ) is a technique that generates a binary decision tree Entrpy is used as a measure to chose the best splitting attribute In ID 3 one child is created for each subcategory while here only two children are created At each step , exhaustive search is used to decide the best split where best is defined by Φ(s/t) = 2 PLPR ∑ | P(Ci / t. L) – P (Ci / t. R )| Here L and R indicate left and right subtrees, PL and PR are the probabilities that the tuple will be on left or right side of the tree P(Ci/TL) denote the probability a tuple is in classs Ci and in the left subtree 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 48

Scalable DT technique SPRINT(Scalable Parallelizable Induction of decision tree It addresses scalability issue by adding parallelism It uses gini index to find the best split If a data set D contains examples from n classes, gini index, gini(D) is defined as gini(D)= 1 - ∑ pj 2 where pj is the relative frequency of class j in D If a data set D is split on A into two subsets D 1 and D 2, the gini index gini(D) is defined as gini split (D) = n 1/n ginii(D 1)+ n 2/n gini(D 2) The attribute provides the smallest ginisplit(D) (or the largest reduction in impurity) is chosen to split the node (need to enumerate all the possible splitting points for each attribute) 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 49

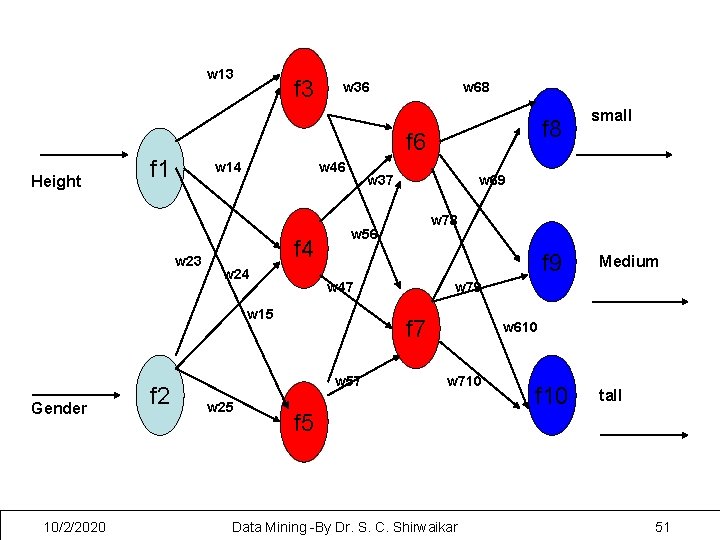
Neural Networks is an information processing system in the form of a graph with many nodes as processing elements (Neurons) and arcs as interconnections between them. NN can be viewed as a directed graph with source (input), sink (output) and internal (hidden) nodes. The input nodes exist in the input layer, output nodes in the output layer and hidden nodes in one or more hidden layers During processing , functions at each node are applied to the input data to produce the output 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 50

w 13 Height f 3 w 36 f 1 w 14 w 46 f 4 w 24 w 37 10/2/2020 w 25 w 78 f 9 w 47 Medium w 79 f 7 w 57 small w 69 w 56 w 15 f 2 f 8 f 6 w 23 Gender w 68 w 610 w 710 f 5 Data Mining -By Dr. S. C. Shirwaikar f 10 tall 51

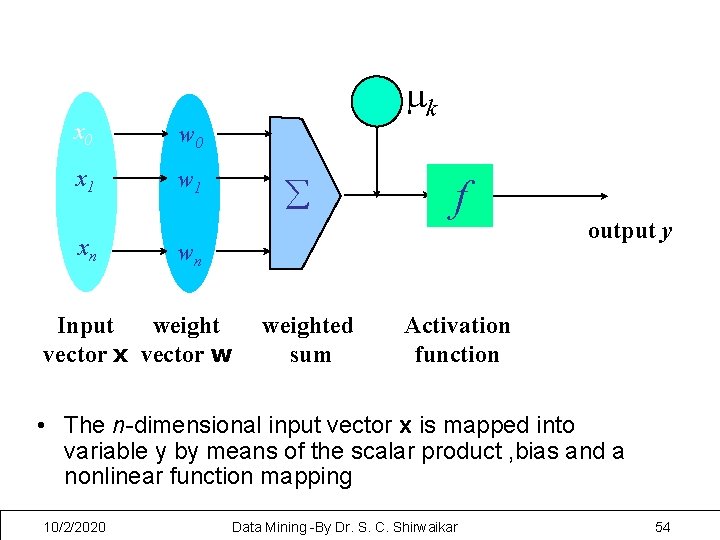
The output of each node I in the NN is based on the definition of function fi, called activation function associated with i. There are many choices for activation functions but are usually threshold functions generating output only if input is above a threshold level Linear- produces a linear output value based on the input fi(s)=cs Threshold or step -The output is 1 or 0 , depending on the sum of the products of the input values abnd their associated weights fi(s)=1 if s >T and 0 otherwise 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 52

Sigmoid – This is a S shaped curve with output values between -1 and 1. fi(s)= 1/(1+e-cs) is a commonly used logistic sigmoid function Hyperbolic tangent – This function has output centered at zero fi(s)=(1– e–s )/(1+e-cs) Nodes in NN have an extra input called bias. This bias value of 1 is input on an arc with a weight of -θ. The effect of the bias input is to move the activation function on the X axis by a value of θ. 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 53

x 0 w 0 x 1 w 1 xn - mk å f wn Input weight vector x vector w weighted sum output y Activation function • The n-dimensional input vector x is mapped into variable y by means of the scalar product , bias and a nonlinear function mapping 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 54

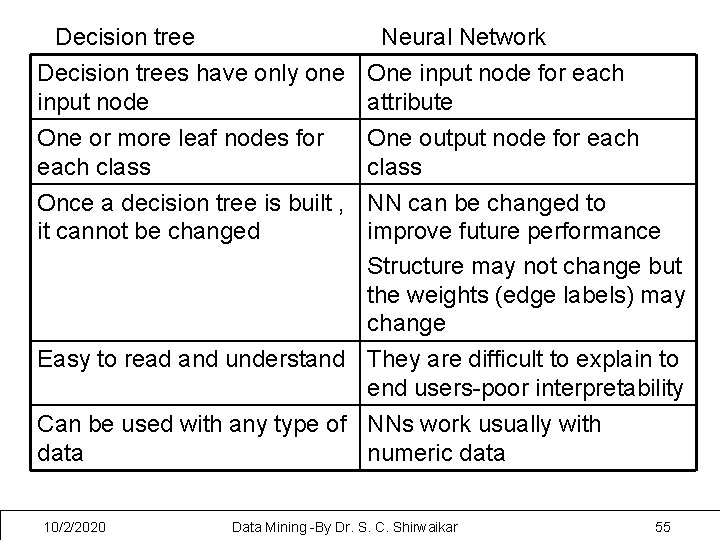
Decision tree Neural Network Decision trees have only one input node One or more leaf nodes for each class One input node for each attribute One output node for each class Once a decision tree is built , NN can be changed to it cannot be changed improve future performance Structure may not change but the weights (edge labels) may change Easy to read and understand They are difficult to explain to end users-poor interpretability Can be used with any type of NNs work usually with data numeric data 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 55

Backpropagation is a neural network learning algorithm. During learning phase, the network learns by adjusting the weights so as to be able to predict the correct class labels of the input tuples Neural Networks involve long training times There are several parameters such as weights , hidden nodes which are determined empirically. It is difficult for human beings to interpret the symbolic meaning behind learned weights or hidden weights and hence are less desirable for data mining –poor interpretability They have high tolerance for noisy data and greater ability to classify patterns on which they are not trained They are well-suited for continuous-valued inputs and outputs. Algorithms are inherently parallel 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 56

The backpropagation algorithm performs learning on a multilayer feed-forward neural network. The input layer only serves to pass the attribute values to the next layer. The network is feed forward in that none of the weights cycles back to an input unit or to an output unit of a previous layer. It is fully connected in that each unit provides input to each unit in the next forward layer 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 57

Defining a network topology • First decide the network topology: No of units in the input layer, No of hidden layers (if > 1), No of units in each hidden layer, and No of units in the output layer • Normalizing the input values for each attribute measured in the training tuples to [0. 0— 1. 0] • One input unit per domain value, each initialized to 0 • One Output unit can be used represent two classes, for classification of more than two classes, one output unit per class is used • Once a network has been trained and its accuracy is unacceptable, repeat the training process with a different network topology or a different set of initial weights 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 58

Backpropagation • Iteratively process a set of training tuples & compare the network's prediction with the actual known target value • For each training tuple, the weights are modified to minimize the mean squared error between the network's prediction and the actual target value • Modifications are made in the “backwards” direction: from the output layer, through each hidden layer down to the first hidden layer, hence “backpropagation” 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 59

Backpropagation Steps 1. Initialize weights (to small random numberss) and biases in the network 2. Propagate the inputs forward Incase of input units output is same as input Incase of hidden or output units compute the net input and the bias and input and compute output by applying activation function 3. For each output unit and hidden units compute the error 4. Backpropagate the error by updating weights and biases 5. The steps 2 to 4 are repeated unitil Terminating condition is satisfied (when error is very small, etc. ) 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 60

Using IF-THEN Rules for Classification Represent the knowledge in the form of IF-THEN rules R: IF age = youth AND student = yes THEN buys_computer = yes “If “ part or left-hand side of rule is called Rule antecedent or precondition “Then” part or right-hand side is called. Rule consequent Assessment of a rule: coverage and accuracy ncovers = No of tuples covered by R ncorrect = No of tuples correctly classified by R coverage(R) = ncovers /|D| D: training data set, | D| is the number of tuples in D accuracy(R) = ncorrect / ncovers 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 61

If a rule R is satisfied by a tuple X then the rule R is said to be triggered by X If only one rule is triggered, rule fires by returning class prediction If more than one rule is triggered, need conflict resolution Size ordering: assign the highest priority to the triggering rules that has the “toughest” requirement (i. e. , with the most attribute test) Class-based ordering: decreasing order of prevalence or misclassification cost per class Rule-based ordering (decision list): rules are organized into one long priority list, according to some measure of rule quality or by experts 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 62

• Rule Extraction from a Decision Tree • Rules are easier to understand than large trees • One rule is created for each path from the root to a leaf • Each attribute-value pair along a path forms a conjunction: the leaf holds the class prediction • Rules are mutually exclusive and exhaustive 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 63

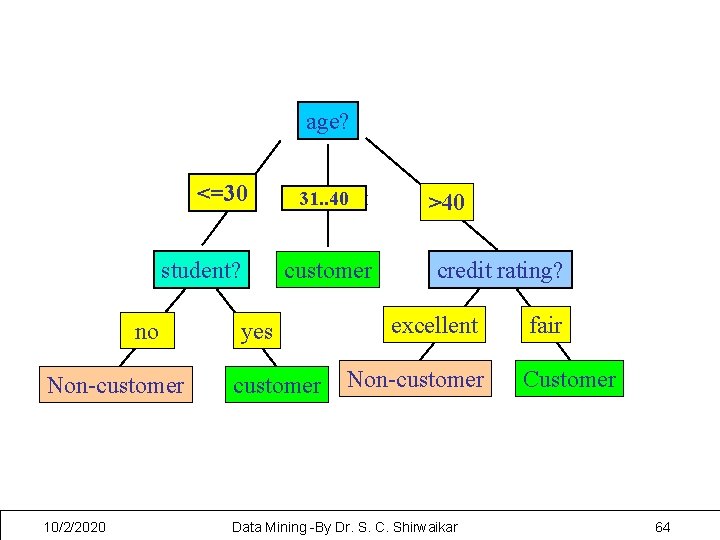
age? <=30 student? no 31. . 40 overcast customer yes >40 credit rating? excellent Non-customer 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar fair Customer 64

• Example: Rule extraction from our buys_computer decisiontree IF age = young AND student = no THEN buys_computer = no IF age = young AND student = yes THEN buys_computer = yes IF age = mid-age THEN buys_computer = yes IF age = old AND credit_rating = excellent THEN buys_computer = yes IF age = young AND credit_rating = fair THEN buys_computer = no 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 65

Rule extraction from networks: Network pruning • Simplify the network structure by removing weighted links that have the least effect on the trained network • Then perform link, unit, or activation value clustering • The set of input and activation values are studied to derive rules describing the relationship between the input and hidden unit layers Sensitivity analysis: assess the impact that a given input variable has on a network output. The knowledge gained from this analysis can be represented in rules 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 66

Rule Extraction from a Training data set • threshold Sequential covering algorithm: Extracts rules directly from training data • Rules are learned sequentially, each for a given class Ci will cover many tuples of Ci but none (or few) of the tuples of other classes • Steps: – Rules are learned one at a time – Each time a rule is learned, the tuples covered by the rules are removed – The process repeats on the remaining tuples unless termination condition, e. g. , when no more training examples or when the quality of a rule returned is below a user-specified 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 67

Combining Techniques Given a classification problem no one classification technique yields the best results • A synthesis of approaches takes multiple techniques and blends them into a new approach Example use linear regression to predict missing values which is then used as input to NN • CMC ( Combination of multiple classifiers) Multiple independent approaches can be applied each yielding its own class prediction. The results are then compared or combined in some manner 10/2/2020 Data Mining -By Dr. S. C. Shirwaikar 68