Classification Classification Classification Classification Features and labels Green

Classification

Classification

Classification

Classification

Features and labels (Green, 6, 4, 4. 5) (Green, 7, 4. 5, 5) (Red, 6, 3, 3. 5) (Red, 4. 5, 4, 4. 5) (Yellow, 1. 5, 8, 2) (Yellow, 1. 5, 7, 2. 5)

Features and labels Objects Features (X) Labels (Y)

Classification (Train) Objects Features (X) Labels (Y)

Classification (Test) (Red, 7, 4, 4. 5) h(Red, 7, 4, 4. 5) ?

Classification (Test) (Red, 5, 3, 4. 5) h(Red, 5, 3, 4. 5) ?

Classification (Test) h(Green, 6, 4, 4. 5) ?

Classification (Test) h(Yellow, 2, 10, 1. 2) ?

Dictionary • Classification, Pattern recognition, Discrimination • X: Features, Explanatory variables, Covariates • Y: Labels, Response variables, Outcome • h(X) : Classifier, hypothesis

Example • Cancer classification: – Y: the tumor is benign or malignant – X: information from the tumor as well as the patient, e. g. size of tumor, shape of tumor, other measurements, etc. – Objective: from what we observe, what is the probability that the tumor is malignant?

Examples More science and technology applications: – handwritten zip code identification – drug discovery (to identify the biological activity of chemical compounds using features describing the chemical structures) – Gene expression analysis ( thousands of features with only dozens of observations)

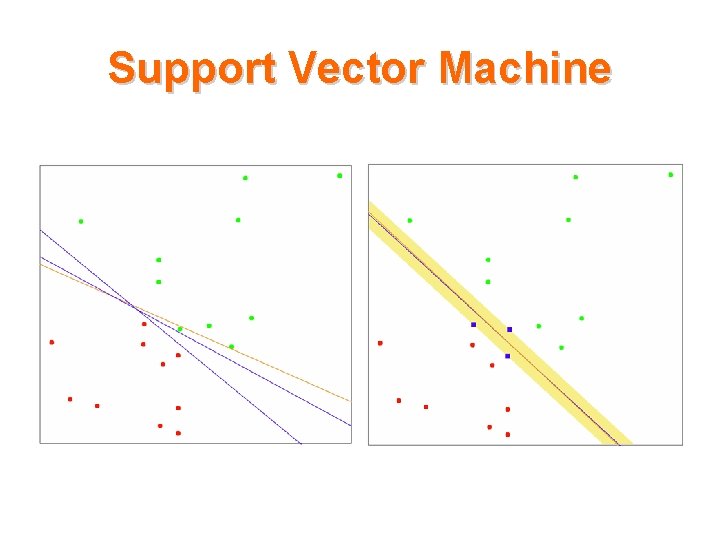
Support Vector Machine • If the data is linearly separable then there exist infinitely many solutions. • Which solution is the best?

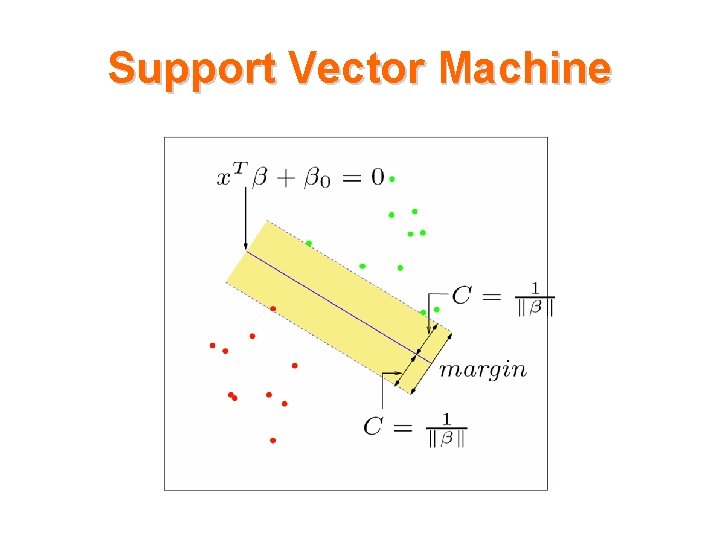
Support Vector Machine Choose the line farthest from both classes. i. e. Choose the line which has the maximum distance from the closest point.
Support Vector Machine

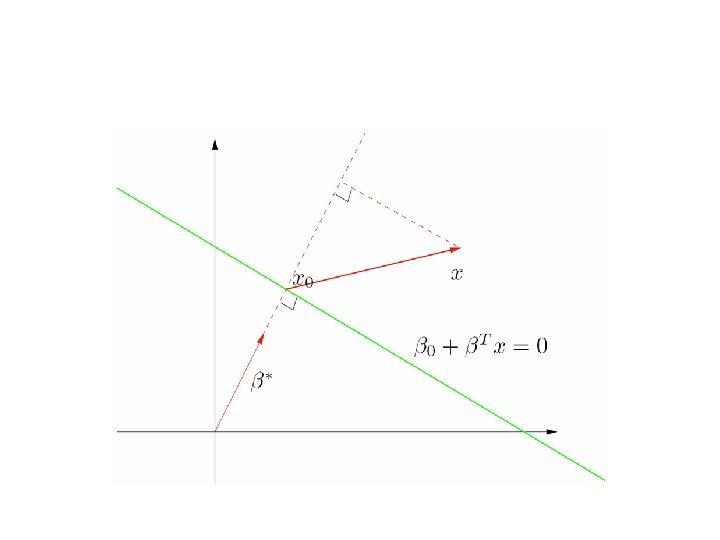
Support Vector Machine

Support Vector Machine
Support Vector Machine

Support Vector Machine

Support Vector Machine

Support Vector Machine

Support Vector Machine

Support Vector Machine

Support Vector Machine

Support Vector Machine

Support Vector Machine

Support Vector Machine

Support Vector Machine

Kernel Methods

Kernel Trick

Observed and Feature

Tasks • Supervised Learning: given examples of inputs and corresponding desired outputs, predict outputs on future inputs. e. g. : classification, regression • Unsupervised Learning: given only inputs, automatically discover representations, features, structure, etc. e. g. : clustering, dimensionality reduction, Feature extraction

Example • Load the sample data, which includes digits 2 and 3 of 64 measurements on a sample of 400. load 2_3. mat • Extract appropriate features by PCA [u s v]=svd(X', 'econ'); • Create data=u(: , 1: 2); • Create a new vector, groups, to classify data into two groups=[zeros(1, 200) ones(1, 200)]; • Randomly select training and test sets. [train, test] = crossvalind('hold. Out', groups);

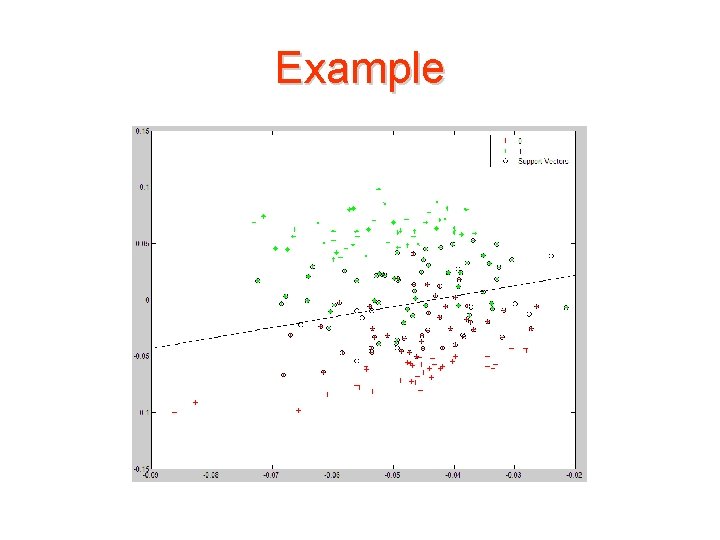
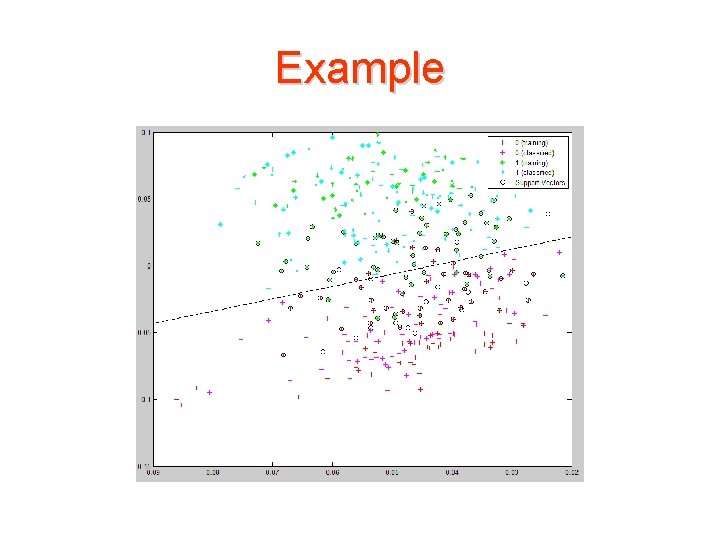
Example • Train an SVM classifier using a linear kernel function and plot the grouped data. svm. Struct = svmtrain(data(train, : ), groups(train), 'showplot', true);
Example

Example • Use the svmclassify function to classify the test set. classes = svmclassify(svm. Struct, data(test, : ), 'showplot', true);
Example

Example • Use Kernel function svm. Struct = svmtrain(data(train, : ), groups(train), 'showplot', true, 'Kernel _Function', 'rbf')
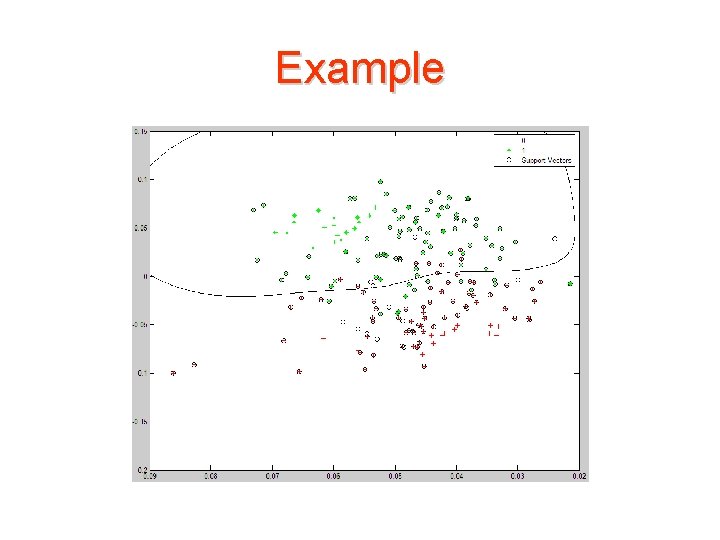
Example

Example • Use the svmclassify function to classify the test set. classes = svmclassify(svm. Struct, data(test, : ), 'showplot', true);
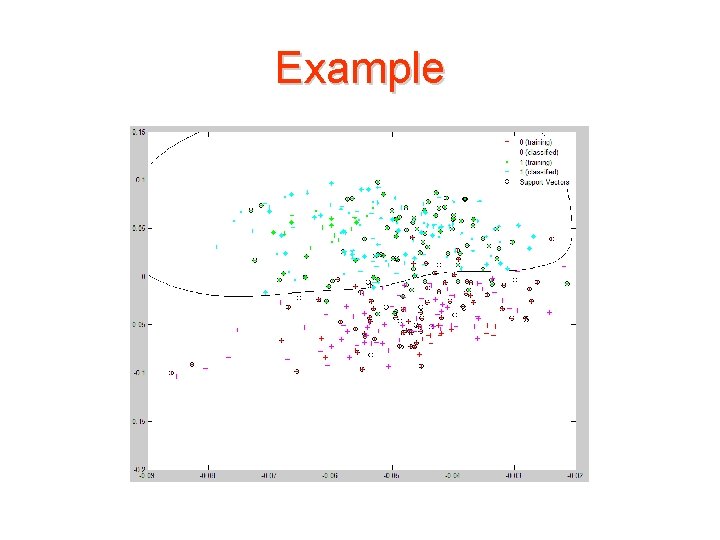
Example
- Slides: 44