Clase N 1 TPN 1 Fuerzas Concentradas Parte

Clase N° 1 – TPN° 1 Fuerzas Concentradas – Parte B Curso de Estática y Resistencia de Materiales Ing. Gabriel Pujol Para las carreas de Ingeniería Industrial de la Facultad de Ingeniería de la Universidad de Buenos Aires

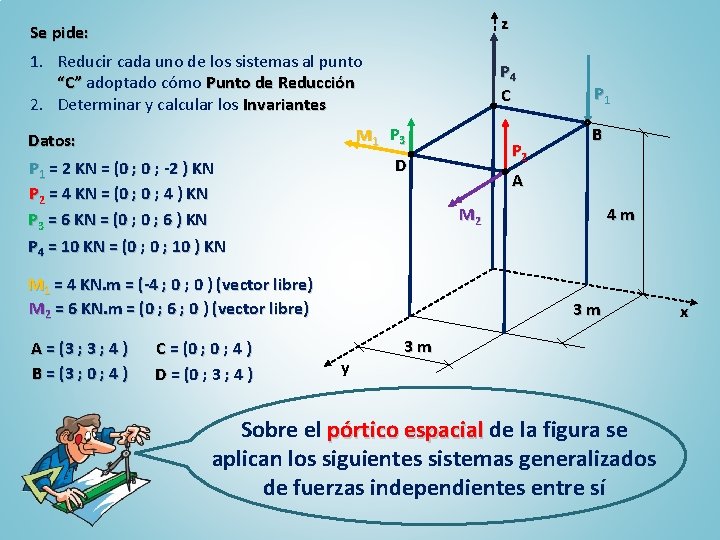
z Se pide: 1. Reducir cada uno de los sistemas al punto “C” adoptado cómo Punto de Reducción 2. Determinar y calcular los Invariantes P 4 C M 1 P 3 Datos: P 1 = 2 KN = (0 ; -2 ) KN P 2 = 4 KN = (0 ; 4 ) KN P 3 = 6 KN = (0 ; 6 ) KN P 4 = 10 KN = (0 ; 10 ) KN C = (0 ; 4 ) D = (0 ; 3 ; 4 ) B A M 2 M 1 = 4 KN. m = (-4 ; 0 ) (vector libre) M 2 = 6 KN. m = (0 ; 6 ; 0 ) (vector libre) A = (3 ; 4 ) B = (3 ; 0 ; 4 ) P 2 D P 1 4 m 3 m y 3 m Sobre el pórtico espacial de la figura se aplican los siguientes sistemas generalizados de fuerzas independientes entre sí x

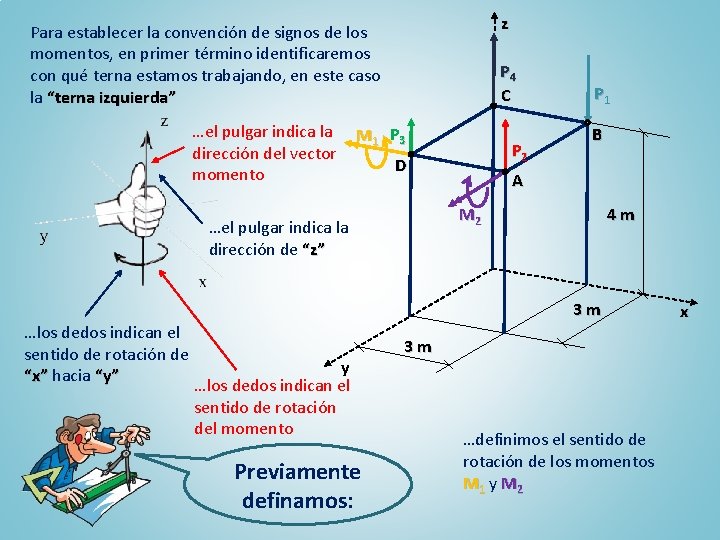
z Para establecer la convención de signos de los momentos, en primer término identificaremos con qué terna estamos trabajando, en este caso la “terna izquierda” …el pulgar indica la dirección del vector momento P 4 C M 1 P 3 P 2 D P 1 B A M 2 …el pulgar indica la dirección de “z” 4 m 3 m …los dedos indican el sentido de rotación de y “x” hacia “y” …los dedos indican el sentido de rotación del momento Previamente definamos: 3 m …definimos el sentido de rotación de los momentos M 1 y M 2 x

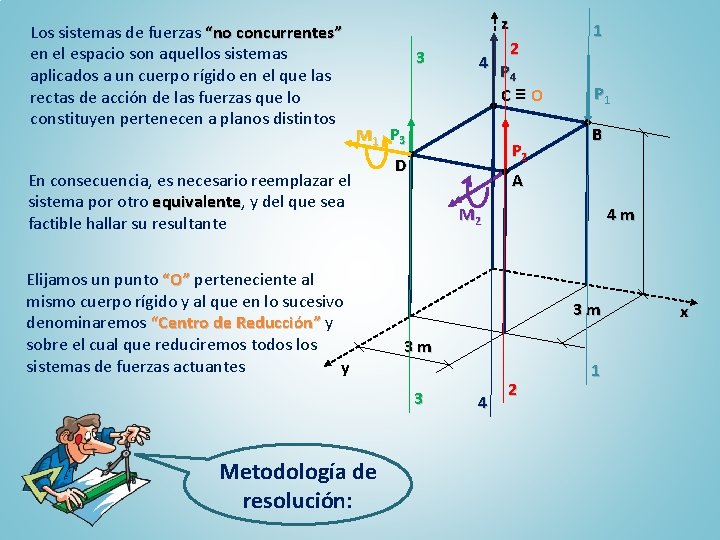
Los sistemas de fuerzas “no concurrentes” en el espacio son aquellos sistemas aplicados a un cuerpo rígido en el que las rectas de acción de las fuerzas que lo constituyen pertenecen a planos distintos z 3 2 4 P 4 C≡O M 1 P 3 En consecuencia, es necesario reemplazar el sistema por otro equivalente, equivalente y del que sea factible hallar su resultante Elijamos un punto “O” perteneciente al mismo cuerpo rígido y al que en lo sucesivo denominaremos “Centro de Reducción” y sobre el cual que reduciremos todos los sistemas de fuerzas actuantes y P 2 D P 1 B A M 2 4 m 3 m 3 m 3 Metodología de resolución: 1 4 2 1 x

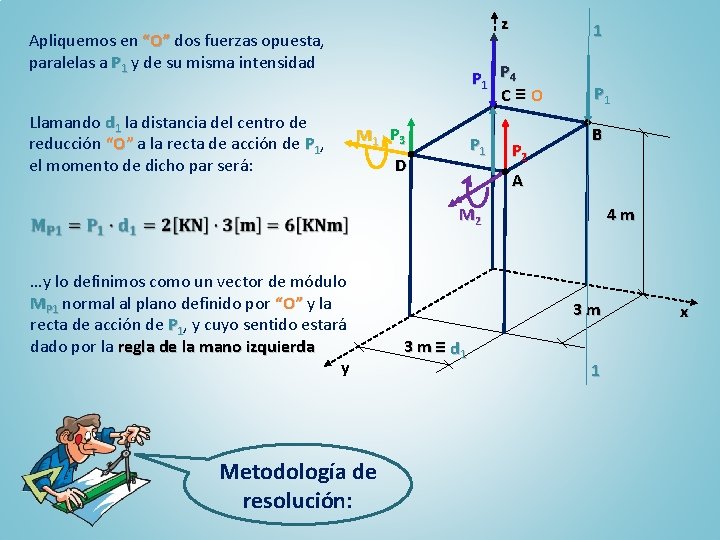
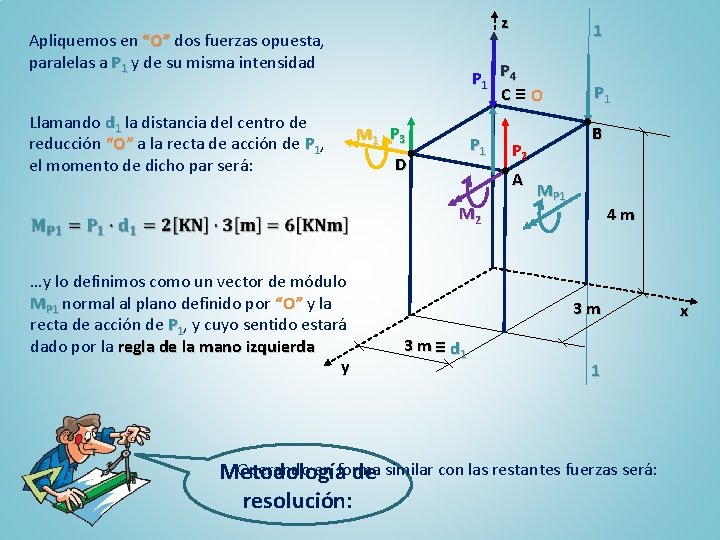
Apliquemos en “O” dos fuerzas opuesta, paralelas a P 1 y de su misma intensidad Llamando d 1 la distancia del centro de reducción “O” a la recta de acción de P 1, el momento de dicho par será: M 1 P 3 z 1 P 4 C≡O P 1 D P 2 B A M 2 …y lo definimos como un vector de módulo MP 1 normal al plano definido por “O” y la recta de acción de P 1, y cuyo sentido estará dado por la regla de la mano izquierda y Metodología de resolución: 4 m 3 m 3 m ≡ d 1 1 x

Apliquemos en “O” dos fuerzas opuesta, paralelas a P 1 y de su misma intensidad Llamando d 1 la distancia del centro de reducción “O” a la recta de acción de P 1, el momento de dicho par será: M 1 P 3 z 1 P 4 C≡O P 1 D …y lo definimos como un vector de módulo MP 1 normal al plano definido por “O” y la recta de acción de P 1, y cuyo sentido estará dado por la regla de la mano izquierda y P 2 A M 2 B MP 1 4 m 3 m 3 m ≡ d 1 1 Operando en forma Metodología de similar con las restantes fuerzas será: resolución: x

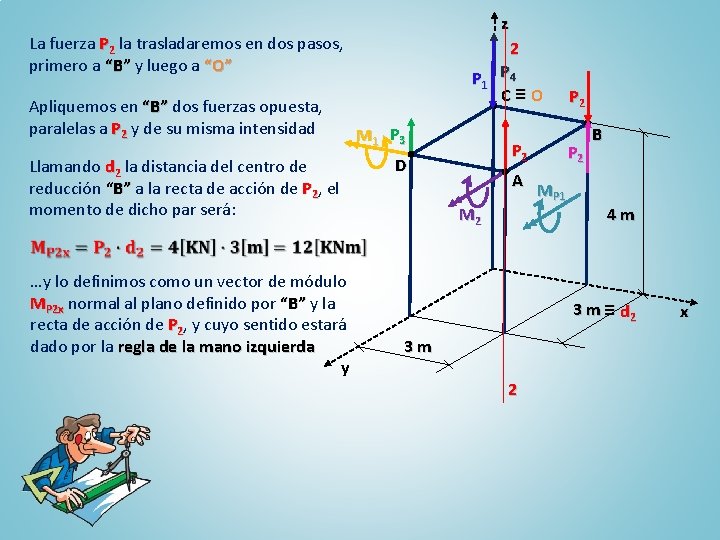
z La fuerza P 2 la trasladaremos en dos pasos, primero a “B” y luego a “O” Apliquemos en “B” dos fuerzas opuesta, paralelas a P 2 y de su misma intensidad Llamando d 2 la distancia del centro de reducción “B” a la recta de acción de P 2, el momento de dicho par será: …y lo definimos como un vector de módulo MP 2 x normal al plano definido por “B” y la recta de acción de P 2, y cuyo sentido estará dado por la regla de la mano izquierda y P 1 M 1 P 3 2 P 4 C≡O P 2 D M 2 A MP 1 P 2 B 4 m 3 m ≡ d 2 3 m 2 x

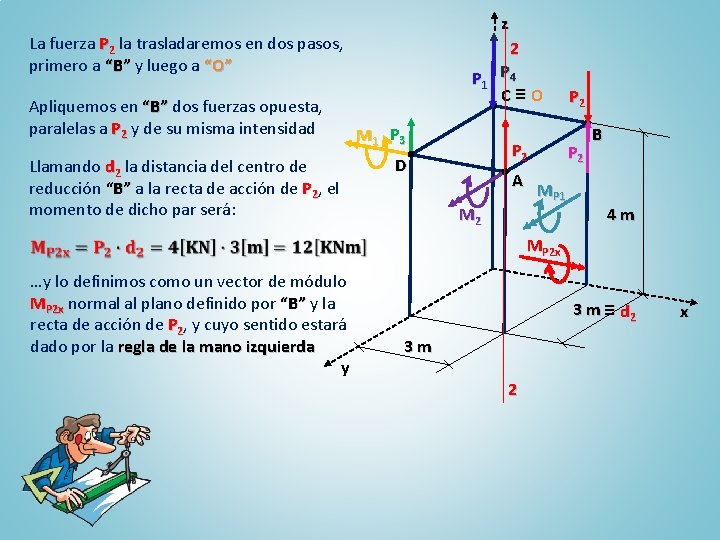
z La fuerza P 2 la trasladaremos en dos pasos, primero a “B” y luego a “O” Apliquemos en “B” dos fuerzas opuesta, paralelas a P 2 y de su misma intensidad Llamando d 2 la distancia del centro de reducción “B” a la recta de acción de P 2, el momento de dicho par será: P 1 M 1 P 3 2 P 4 C≡O P 2 D M 2 A MP 1 P 2 B 4 m MP 2 x …y lo definimos como un vector de módulo MP 2 x normal al plano definido por “B” y la recta de acción de P 2, y cuyo sentido estará dado por la regla de la mano izquierda y 3 m ≡ d 2 3 m 2 x

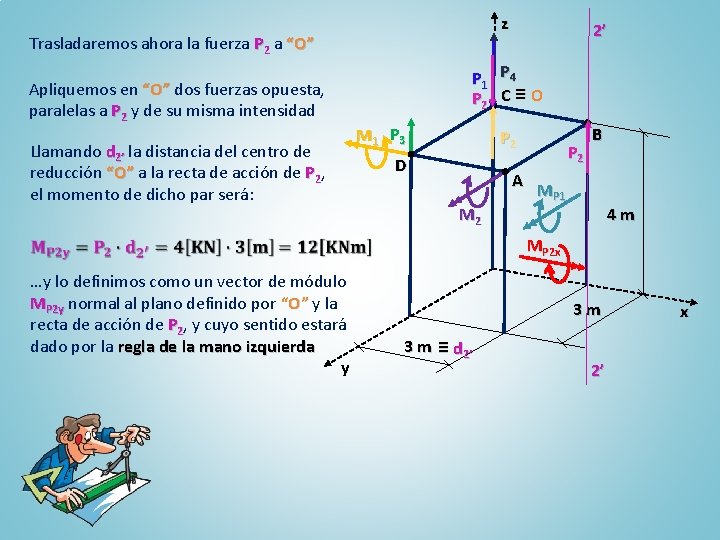
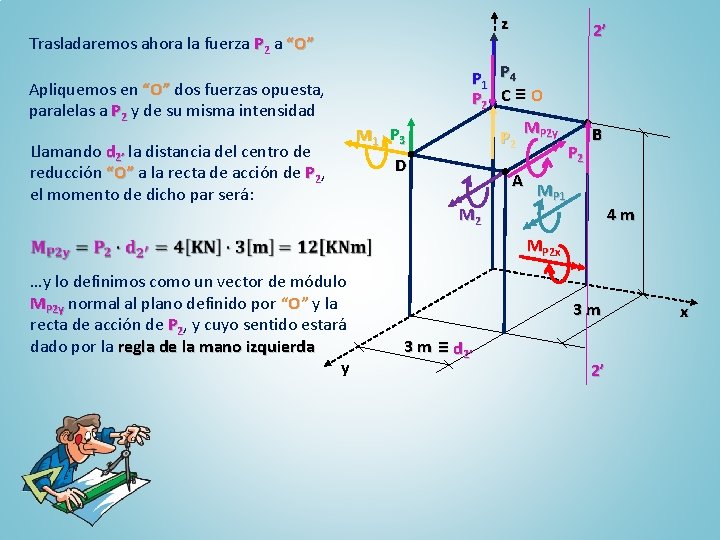
z Trasladaremos ahora la fuerza P 2 a “O” Apliquemos en “O” dos fuerzas opuesta, paralelas a P 2 y de su misma intensidad Llamando d 2’ la distancia del centro de reducción “O” a la recta de acción de P 2, el momento de dicho par será: 2’ P 1 P 4 P 2 C ≡ O M 1 P 3 P 2 D M 2 P 2 B A MP 1 4 m MP 2 x …y lo definimos como un vector de módulo MP 2 y normal al plano definido por “O” y la recta de acción de P 2, y cuyo sentido estará dado por la regla de la mano izquierda y 3 m 3 m ≡ d 2’ 2’ x

z Trasladaremos ahora la fuerza P 2 a “O” Apliquemos en “O” dos fuerzas opuesta, paralelas a P 2 y de su misma intensidad Llamando d 2’ la distancia del centro de reducción “O” a la recta de acción de P 2, el momento de dicho par será: 2’ P 1 P 4 P 2 C ≡ O M 1 P 3 P 2 D M 2 MP 2 y P 2 B A MP 1 4 m MP 2 x …y lo definimos como un vector de módulo MP 2 y normal al plano definido por “O” y la recta de acción de P 2, y cuyo sentido estará dado por la regla de la mano izquierda y 3 m 3 m ≡ d 2’ 2’ x

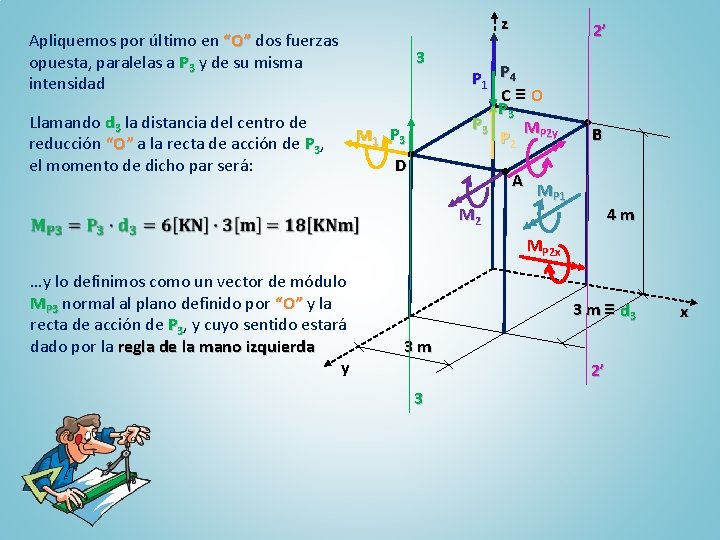
z Apliquemos por último en “O” dos fuerzas opuesta, paralelas a P 3 y de su misma intensidad Llamando d 3 la distancia del centro de reducción “O” a la recta de acción de P 3, el momento de dicho par será: 3 M 1 P 3 2’ P 1 P 4 C≡O P 3 M P 2 y D M 2 B A MP 1 4 m MP 2 x …y lo definimos como un vector de módulo MP 3 normal al plano definido por “O” y la recta de acción de P 3, y cuyo sentido estará dado por la regla de la mano izquierda y 3 m ≡ d 3 3 m 2’ 3 x

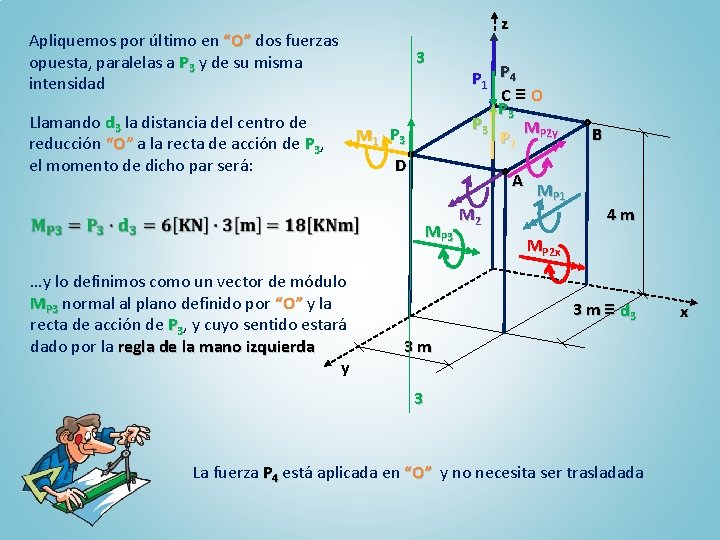
z Apliquemos por último en “O” dos fuerzas opuesta, paralelas a P 3 y de su misma intensidad Llamando d 3 la distancia del centro de reducción “O” a la recta de acción de P 3, el momento de dicho par será: 3 M 1 P 3 D MP 3 …y lo definimos como un vector de módulo MP 3 normal al plano definido por “O” y la recta de acción de P 3, y cuyo sentido estará dado por la regla de la mano izquierda y P 1 P 4 C≡O P 3 M P 2 y M 2 A MP 1 B 4 m MP 2 x 3 m ≡ d 3 3 m 3 La fuerza P 4 está aplicada en “O” y no necesita ser trasladada x

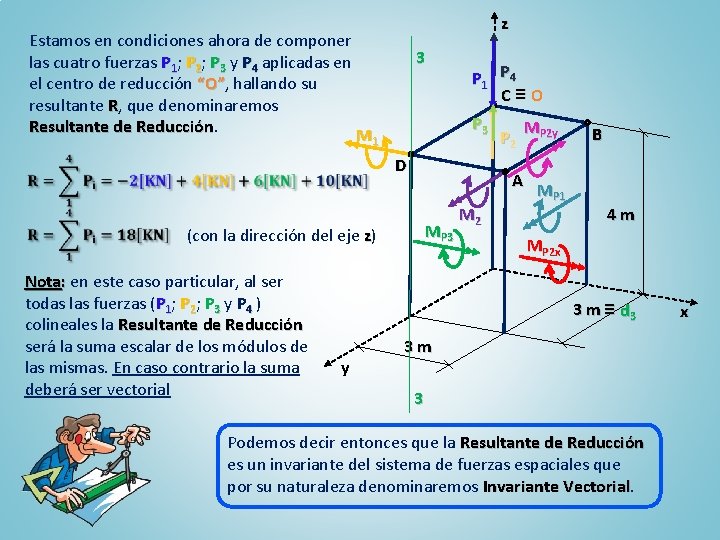
z Estamos en condiciones ahora de componer las cuatro fuerzas P 1; P 2; P 3 y P 4 aplicadas en el centro de reducción “O”, “O” hallando su resultante R, que denominaremos Resultante de Reducción M 3 P 1 P 4 C≡O P 3 1 D MP 3 (con la dirección del eje z) Nota: en este caso particular, al ser todas las fuerzas (P 1; P 2; P 3 y P 4 ) colineales la Resultante de Reducción será la suma escalar de los módulos de las mismas. En caso contrario la suma deberá ser vectorial M 2 P 2 MP 2 y A MP 1 B 4 m MP 2 x 3 m ≡ d 3 y 3 m 3 Podemos decir entonces que la Resultante de Reducción es un invariante del sistema de fuerzas espaciales que por su naturaleza denominaremos Invariante Vectorial x

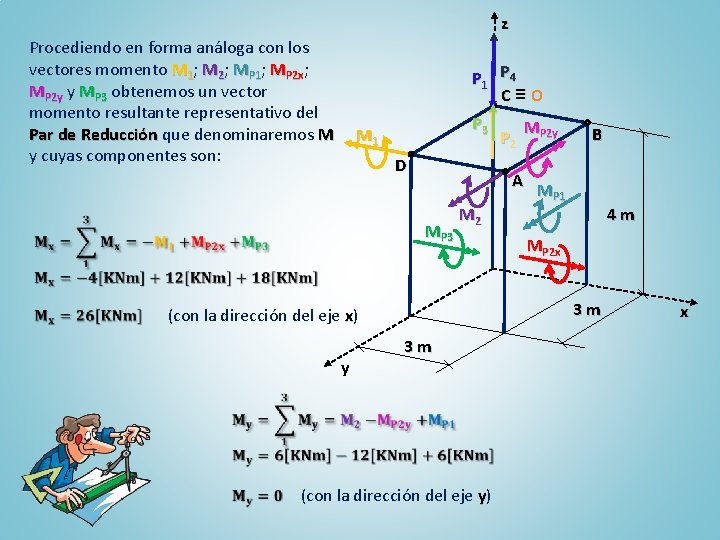
z Procediendo en forma análoga con los vectores momento M 1; M 2; MP 1; MP 2 x; MP 2 y y MP 3 obtenemos un vector momento resultante representativo del Par de Reducción que denominaremos M y cuyas componentes son: P 1 P 4 C≡O P 3 M 1 D MP 3 M 2 MP 2 y B A MP 1 4 m MP 2 x 3 m (con la dirección del eje x) y P 2 3 m (con la dirección del eje y) x

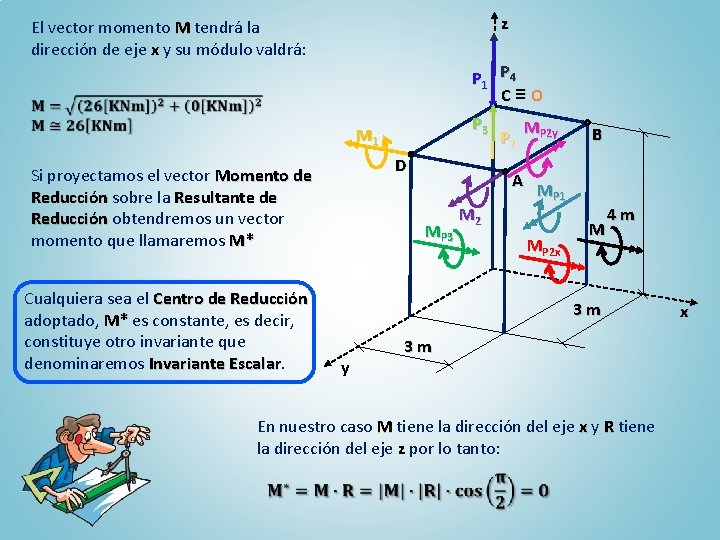
z El vector momento M tendrá la dirección de eje x y su módulo valdrá: P 1 P 4 C≡O P 3 M 1 D Si proyectamos el vector Momento de Reducción sobre la Resultante de Reducción obtendremos un vector momento que llamaremos M* Cualquiera sea el Centro de Reducción adoptado, M* es constante, es decir, constituye otro invariante que denominaremos Invariante Escalar MP 3 M 2 P 2 MP 2 y B A MP 1 MP 2 x M 4 m 3 m y 3 m En nuestro caso M tiene la dirección del eje x y R tiene la dirección del eje z por lo tanto: x

Bibliografía Estabilidad I – Enrique Fliess Introducción a la Estática y Resistencia de Materiales – C. Raffo

Muchas Gracias