Chapter3 Direct Kinematic Model VDP Rotation Matrices in









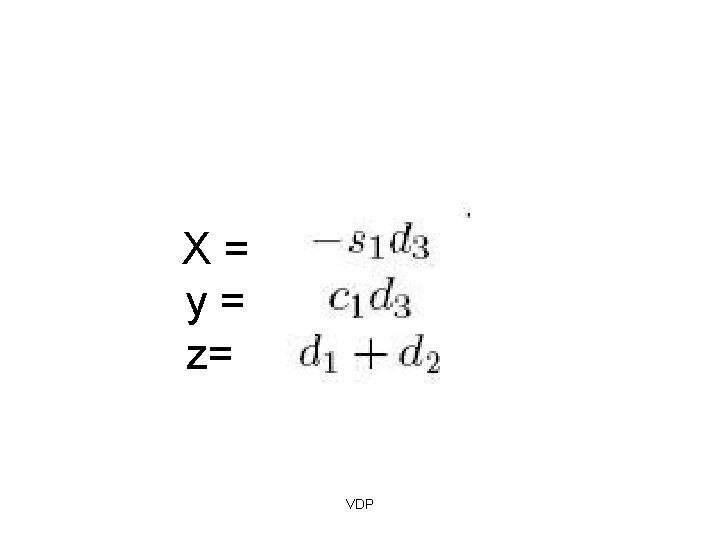




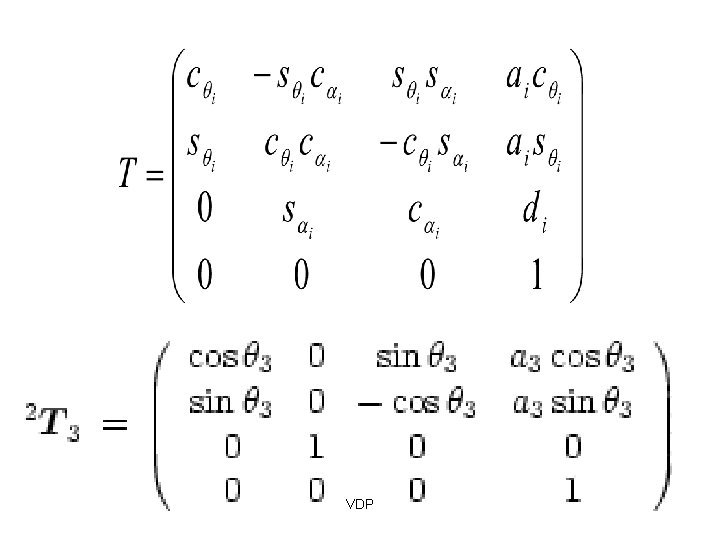
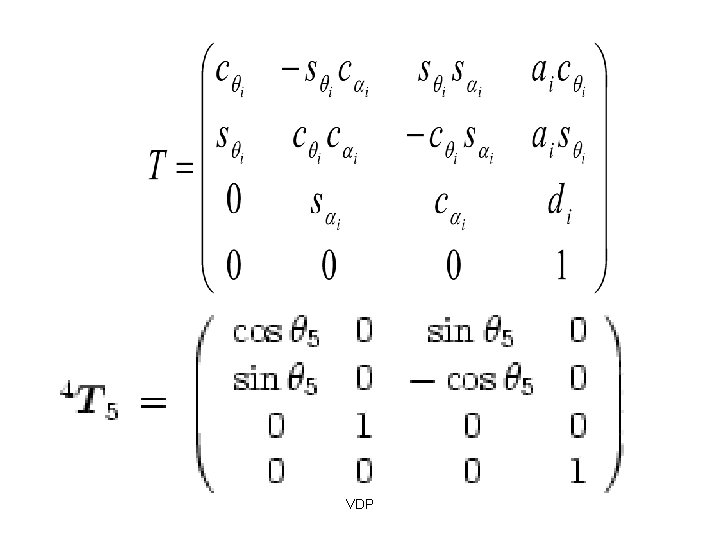
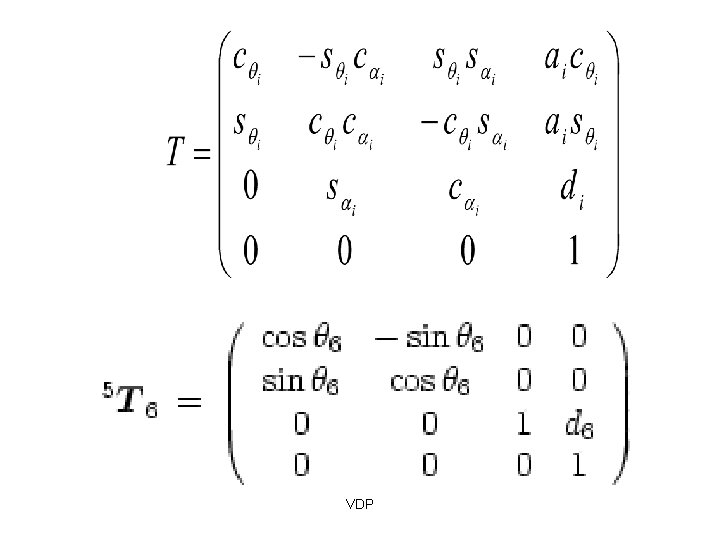

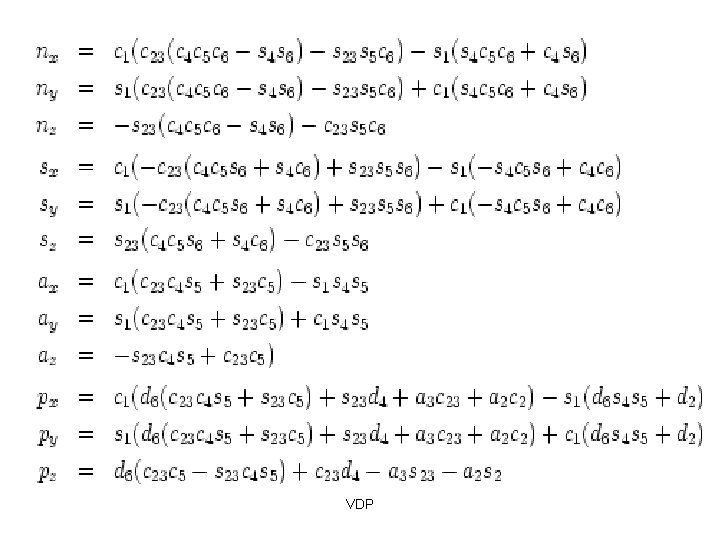
- Slides: 63

Chapter-3 Direct Kinematic Model VDP

Rotation Matrices in 3 D , lets return from homogenous representation Rotation around the Z-Axis Rotation around the Y-Axis Rotation around the X-Axis VDP

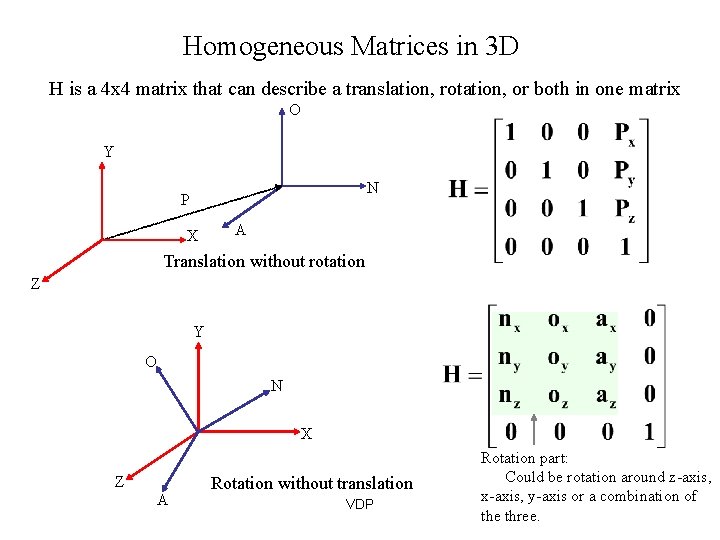
Homogeneous Matrices in 3 D H is a 4 x 4 matrix that can describe a translation, rotation, or both in one matrix O Y N P X A Translation without rotation Z Y O N X Z A Rotation without translation VDP Rotation part: Could be rotation around z-axis, x-axis, y-axis or a combination of the three.

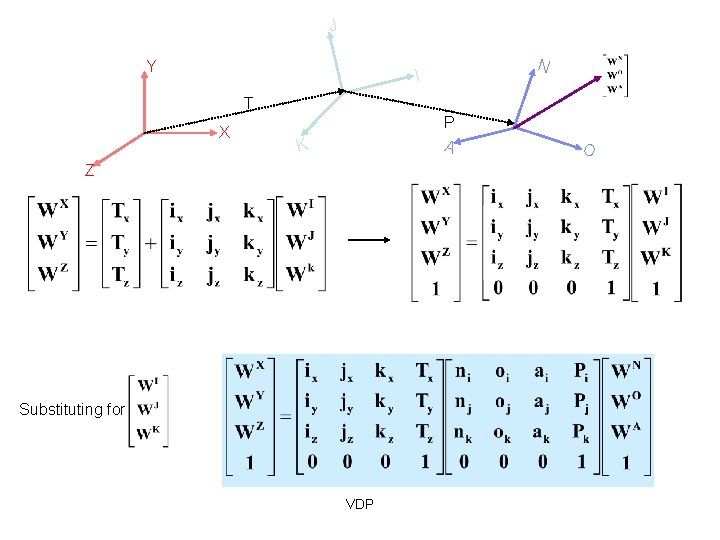
J Y N I T X P A K Z Substituting for VDP O

Notice that H can also be written as: Product of the two matrices H = (Translation relative to the XYZ frame) * (Rotation relative to the XYZ frame) * (Translation relative to the IJK frame) * (Rotation relative to the IJK frame) VDP

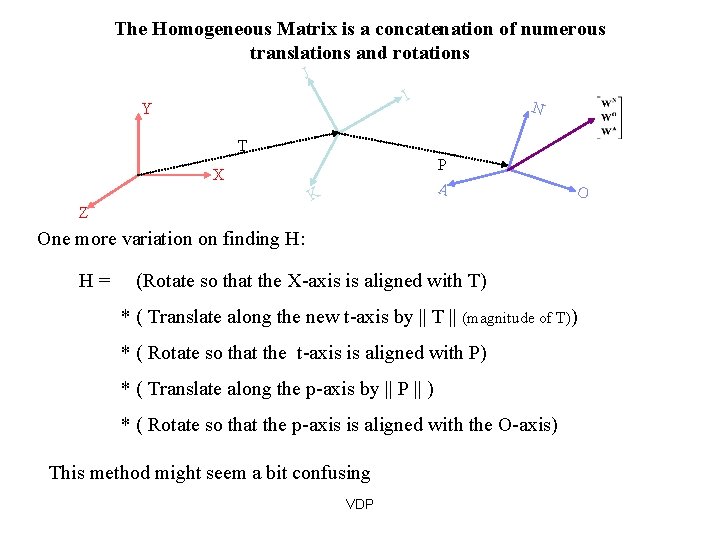
The Homogeneous Matrix is a concatenation of numerous translations and rotations J I Y N T P A X K Z O One more variation on finding H: H= (Rotate so that the X-axis is aligned with T) * ( Translate along the new t-axis by || T || (magnitude of T)) * ( Rotate so that the t-axis is aligned with P) * ( Translate along the p-axis by || P || ) * ( Rotate so that the p-axis is aligned with the O-axis) This method might seem a bit confusing VDP

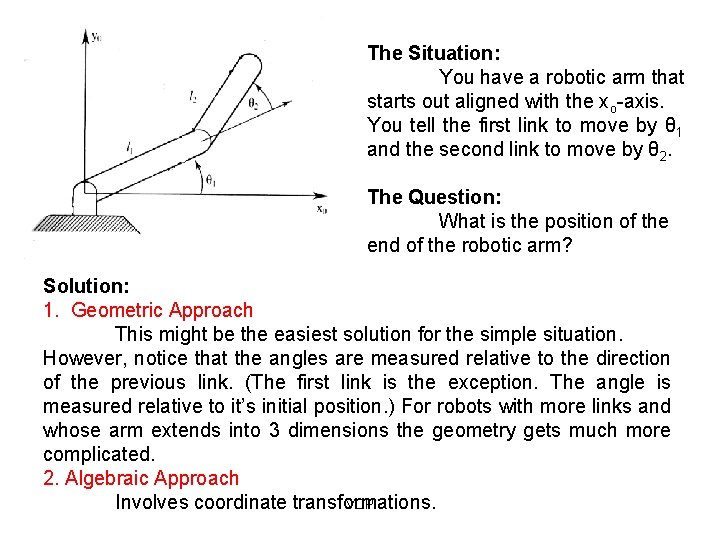
The Situation: You have a robotic arm that starts out aligned with the xo-axis. You tell the first link to move by θ 1 and the second link to move by θ 2. The Question: What is the position of the end of the robotic arm? Solution: 1. Geometric Approach This might be the easiest solution for the simple situation. However, notice that the angles are measured relative to the direction of the previous link. (The first link is the exception. The angle is measured relative to it’s initial position. ) For robots with more links and whose arm extends into 3 dimensions the geometry gets much more complicated. 2. Algebraic Approach VDP Involves coordinate transformations.

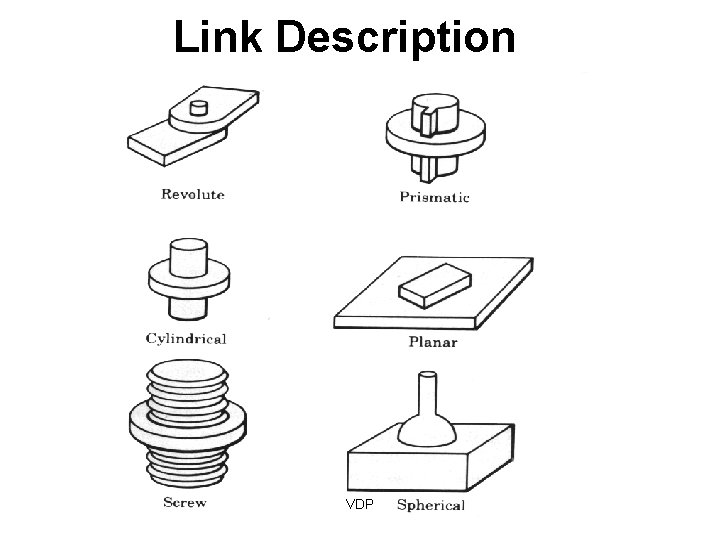
Link Description VDP

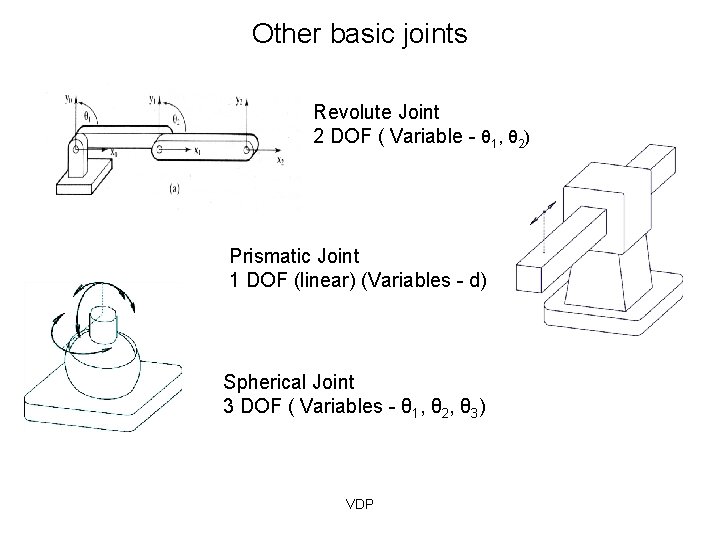
Other basic joints Revolute Joint 2 DOF ( Variable - θ 1, θ 2) Prismatic Joint 1 DOF (linear) (Variables - d) Spherical Joint 3 DOF ( Variables - θ 1, θ 2, θ 3) VDP

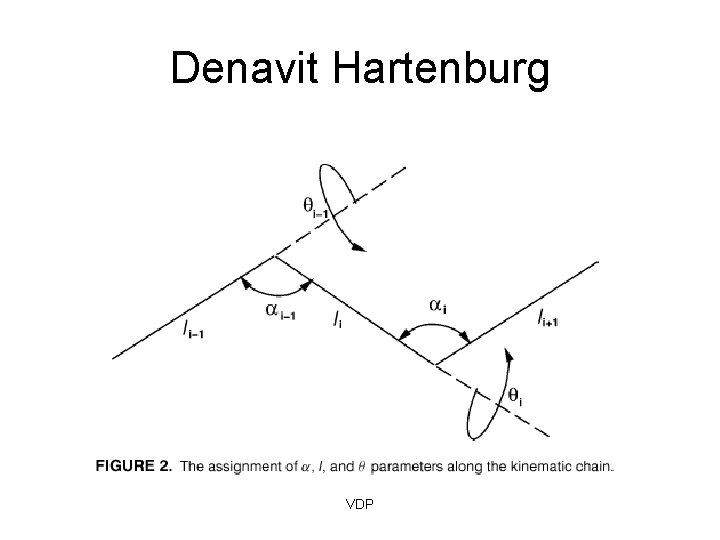
History of Matrix Representation • Method introduced in 1955 by Denavit and Hartenburg • Matrix representation is known as the Denavit-Hartenburg (D-H) representation of linkages VDP

Denavit-Hartenburg (D-H) representation • Describe the rotation and translation relationship between adjacent link. • D-H representation results in a 4 X 4 homogenous transformation matrix representing each link’s coordinate system at the joint with respect previous link’s coordinate system VDP

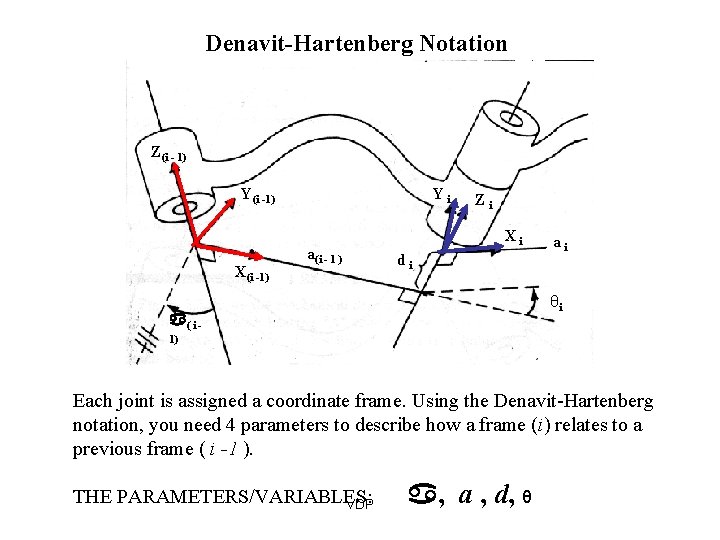
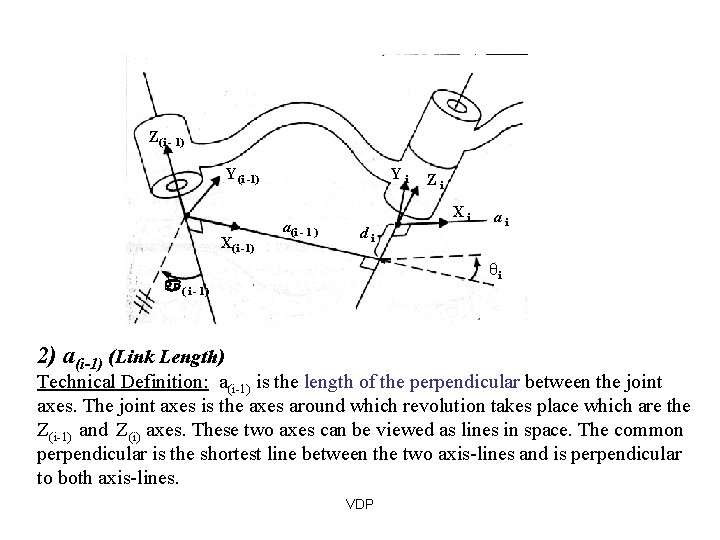
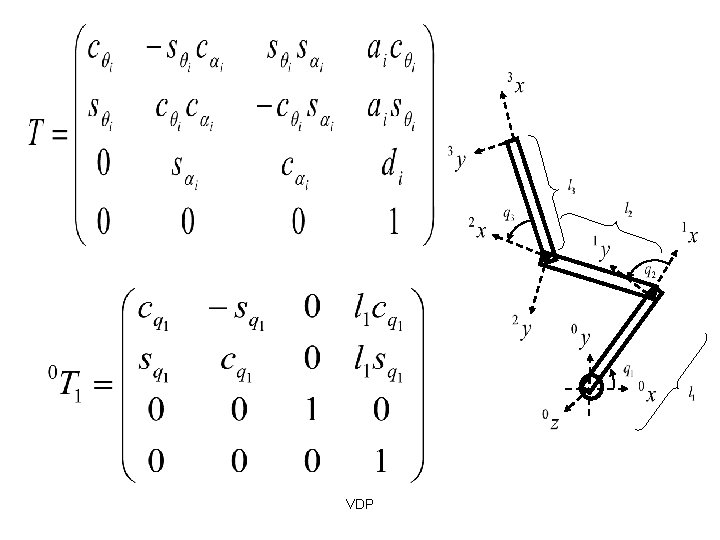
Denavit-Hartenberg Notation Z(i - 1) Y(i -1) X(i -1) Yi a(i - 1 ) Zi Xi di ai θi ( i 1) Each joint is assigned a coordinate frame. Using the Denavit-Hartenberg notation, you need 4 parameters to describe how a frame (i) relates to a previous frame ( i -1 ). THE PARAMETERS/VARIABLES: VDP , a , d, θ

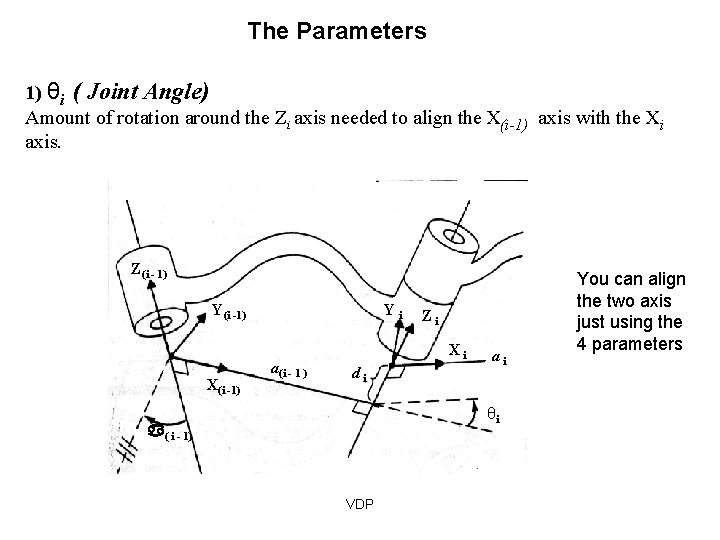
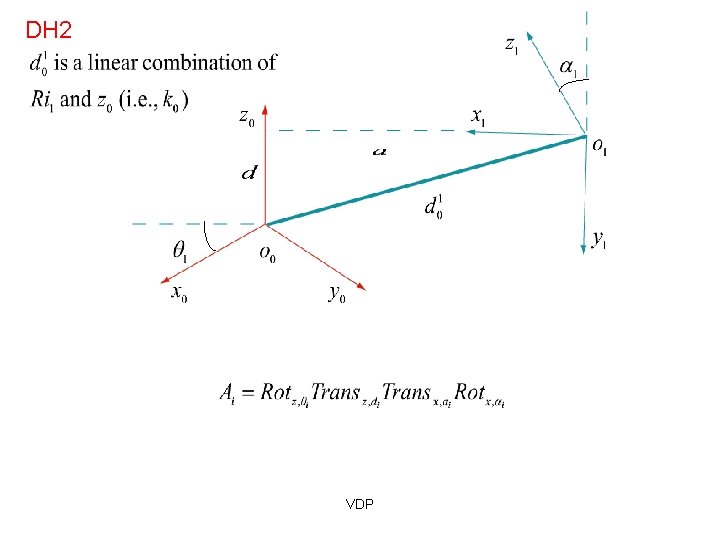
The Parameters 1) θi ( Joint Angle) Amount of rotation around the Zi axis needed to align the X(i-1) axis with the Xi axis. Z(i - 1) Y(i -1) X(i -1) Yi a(i - 1 ) Zi Xi di ai θi ( i - 1) VDP You can align the two axis just using the 4 parameters

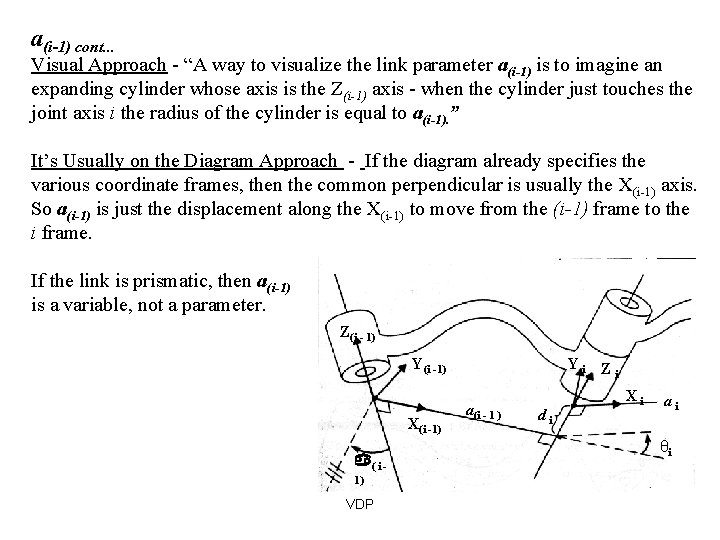
Z(i - 1) Y(i -1) X(i -1) Yi a(i - 1 ) Zi Xi di ai θi ( i - 1) 2) a(i-1) (Link Length) Technical Definition: a(i-1) is the length of the perpendicular between the joint axes. The joint axes is the axes around which revolution takes place which are the Z(i-1) and Z(i) axes. These two axes can be viewed as lines in space. The common perpendicular is the shortest line between the two axis-lines and is perpendicular to both axis-lines. VDP

a(i-1) cont. . . Visual Approach - “A way to visualize the link parameter a(i-1) is to imagine an expanding cylinder whose axis is the Z(i-1) axis - when the cylinder just touches the joint axis i the radius of the cylinder is equal to a(i-1). ” It’s Usually on the Diagram Approach - If the diagram already specifies the various coordinate frames, then the common perpendicular is usually the X(i-1) axis. So a(i-1) is just the displacement along the X(i-1) to move from the (i-1) frame to the i frame. If the link is prismatic, then a(i-1) is a variable, not a parameter. Z(i - 1) Y(i -1) X(i -1) ( i 1) VDP Yi a(i - 1 ) di Zi Xi ai θi

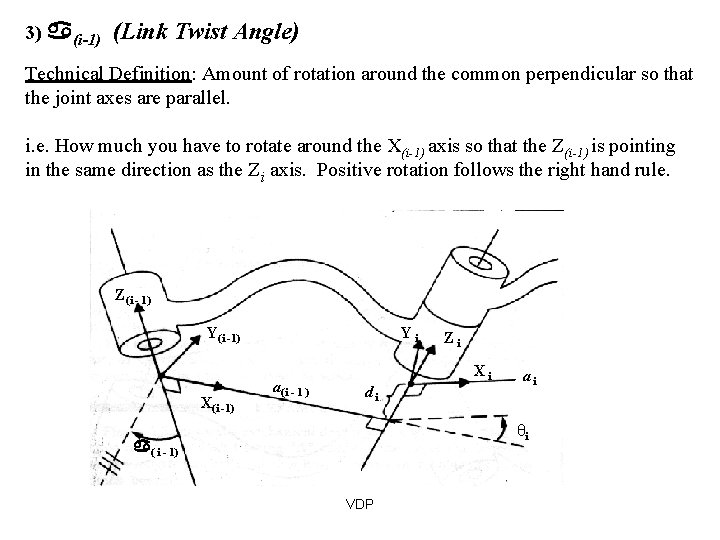
3) (i-1) (Link Twist Angle) Technical Definition: Amount of rotation around the common perpendicular so that the joint axes are parallel. i. e. How much you have to rotate around the X(i-1) axis so that the Z(i-1) is pointing in the same direction as the Zi axis. Positive rotation follows the right hand rule. Z(i - 1) Y(i -1) X(i -1) Yi a(i - 1 ) Zi Xi di ai θi ( i - 1) VDP

Denavit Hartenburg VDP

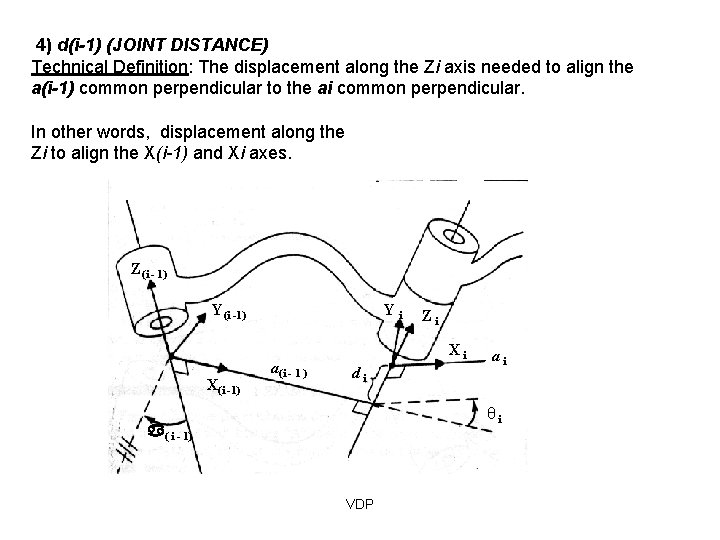
4) d(i-1) (JOINT DISTANCE) Technical Definition: The displacement along the Zi axis needed to align the a(i-1) common perpendicular to the ai common perpendicular. In other words, displacement along the Zi to align the X(i-1) and Xi axes. Z(i - 1) Y(i -1) X(i -1) Yi a(i - 1 ) Zi Xi di ai θi ( i - 1) VDP

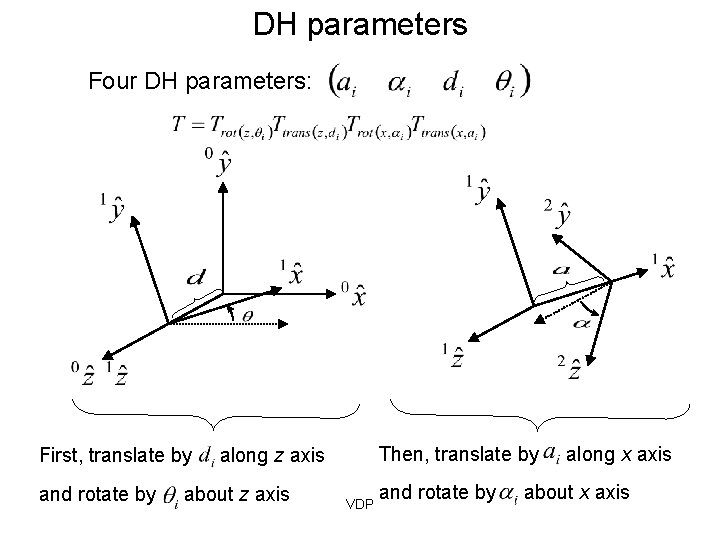
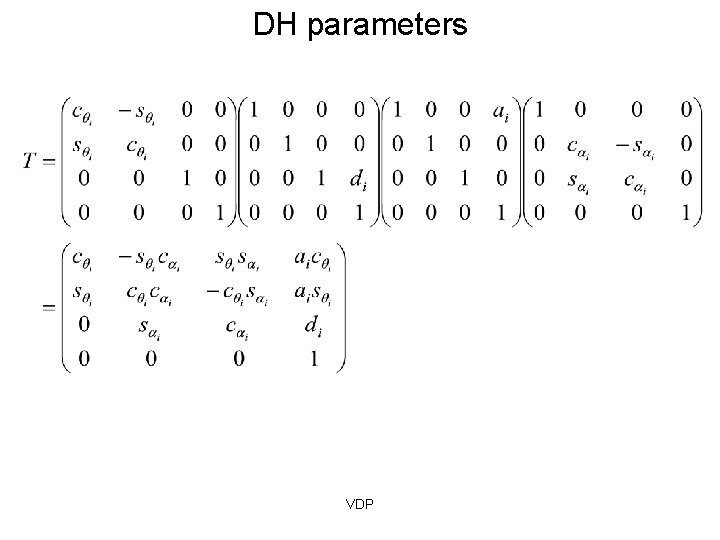
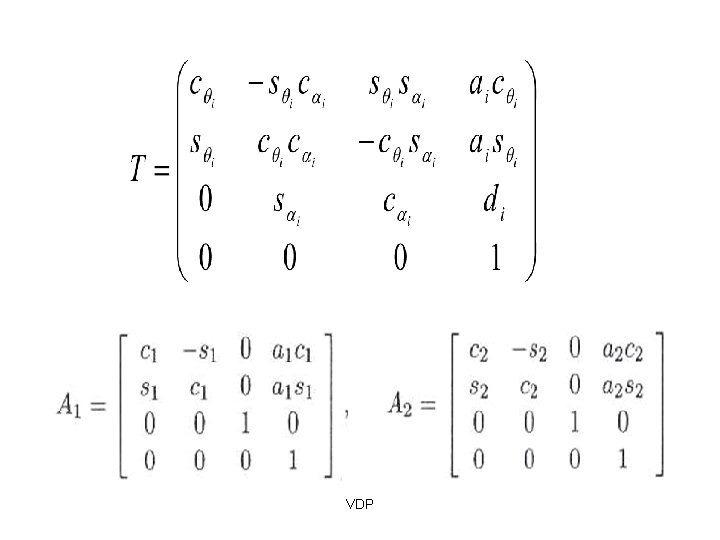
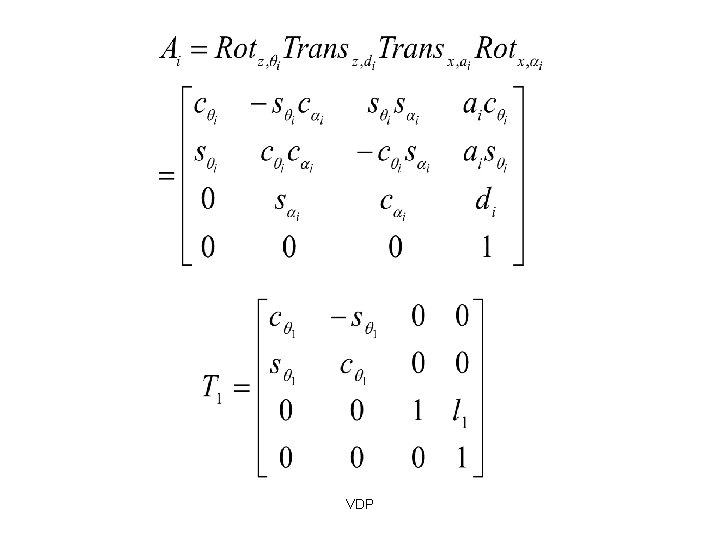
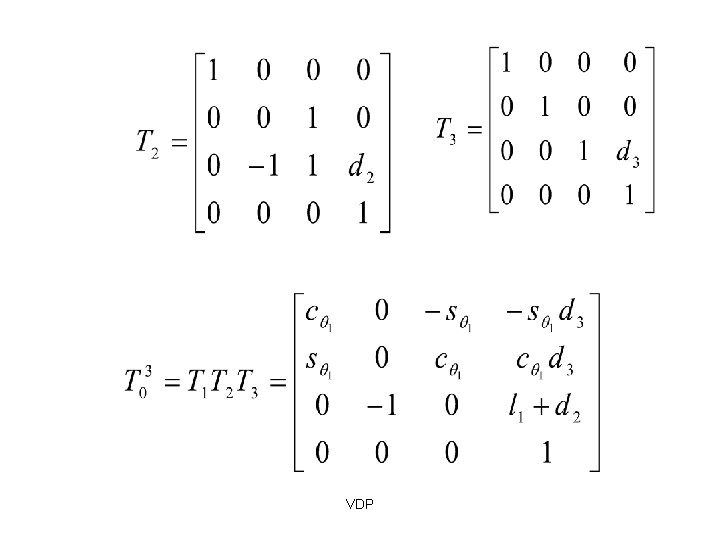
DH parameters Four DH parameters: First, translate by and rotate by Then, translate by along z axis about z axis VDP and rotate by along x axis about x axis

DH parameters These four DH parameters, represent the following homogeneous matrix: First, translate by and rotate by Then, translate by along z axis and rotate by about z axis (JOINT PARAMETER) VDP along x axis about x axis (LINK PARAMETER)

DH parameters VDP

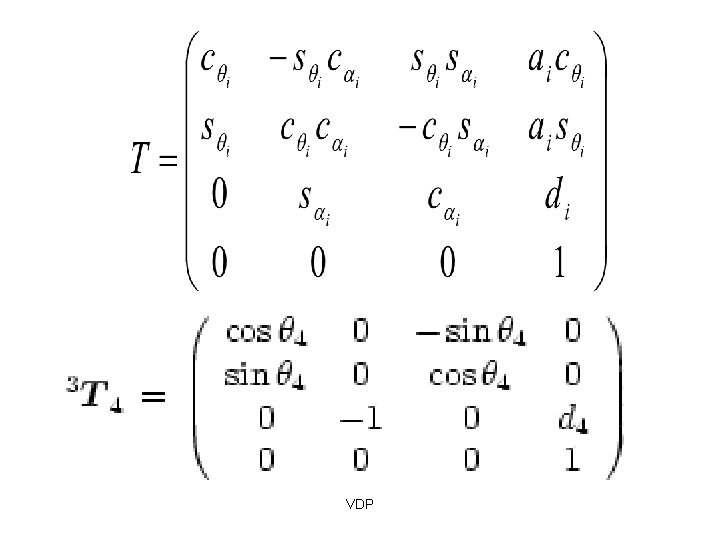
The Denavit-Hartenberg Matrix Just like the Homogeneous Matrix, the Denavit-Hartenberg Matrix is a transformation matrix from one coordinate frame to the next. Using a series of D-H Matrix multiplications and the D-H Parameter table, the final result is a transformation matrix from some frame to your initial frame. VDP

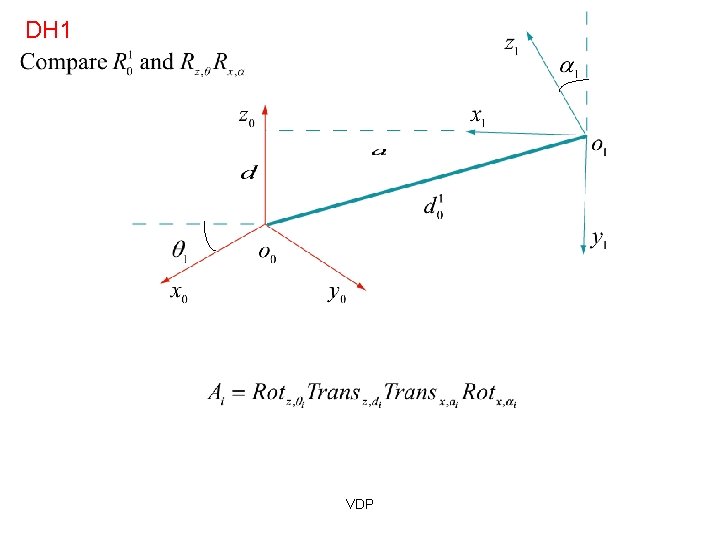
DH 1 VDP

DH 2 VDP

Denavit-Hartenberg Convention • Number the joints from 1 to n starting with the base and ending with the end-effector. • Establish the base coordinate system. Establish a right-handed orthonormal coordinate system at the supporting base with axis lying along the axis of motion of joint 1. • Establish joint axis. Align the Zi with the axis of motion (rotary or sliding) of joint i+1. • Establish the origin of the ith coordinate system. Locate the origin of the ith coordinate at the intersection of the Zi & Zi-1 or at the intersection of common normal between the Zi & Zi-1 axes and the Zi axis. • Establish Xi axis. Establish or along the common normal between the Zi-1 & Zi axes when they are parallel. • Establish Yi axis. Assign to complete the right -handed coordinate system. • Find the link and joint parameters

Direct Kinematics Algorithm 1) Draw sketch 2) Number links. Base=0, Last link = n 3) Identify and number robot joints 4) Draw axis Zi for joint I 5) Determine link length ai-1 between Zi-1 and Zi 6) Draw axis Xi-1 7) Determine link twist i-1 measured around Xi-1 8) Determine the joint offset di 9) Determine joint angle i around Zi VDP

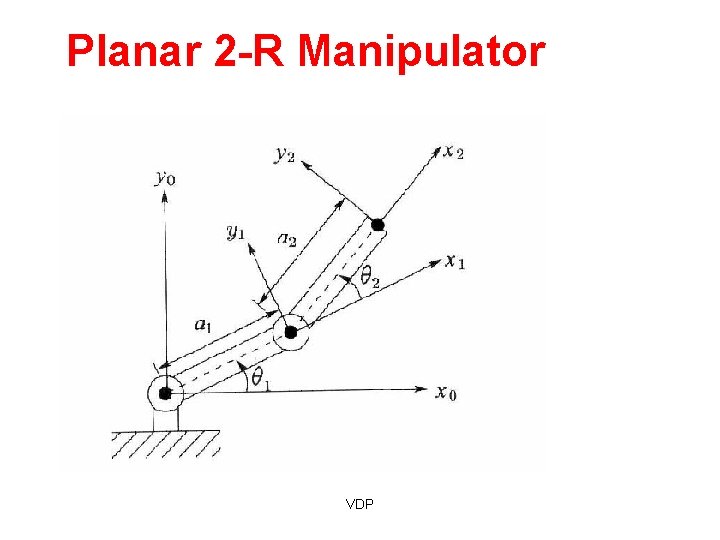
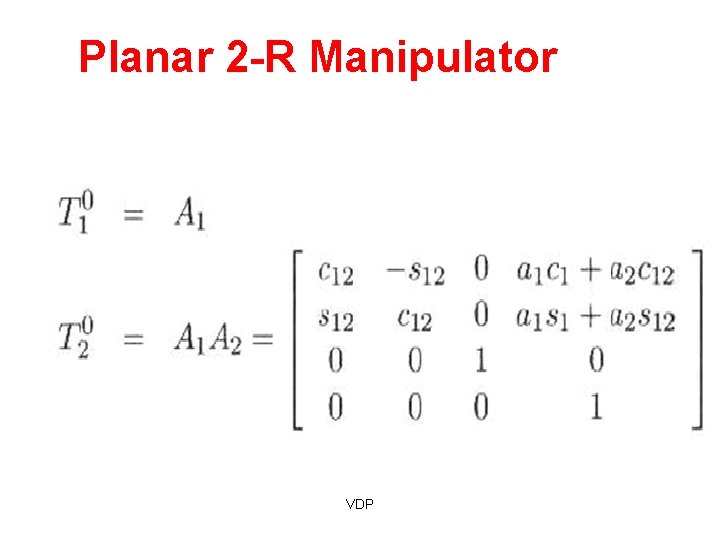
Planar 2 -R Manipulator VDP

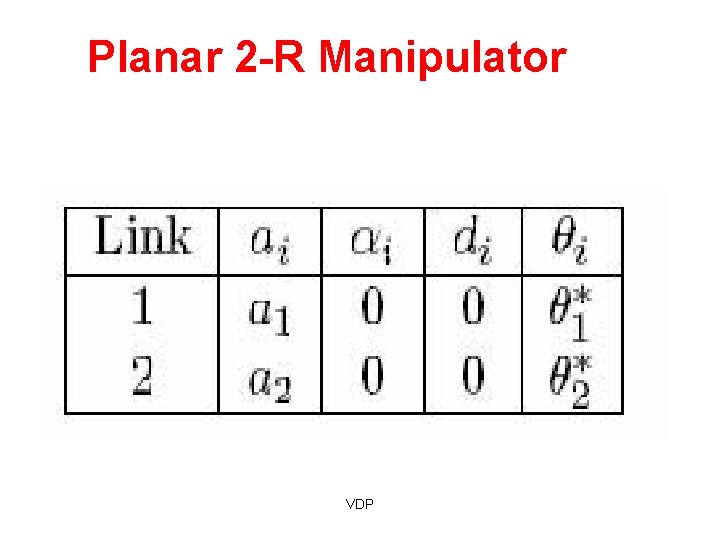
Planar 2 -R Manipulator VDP

VDP

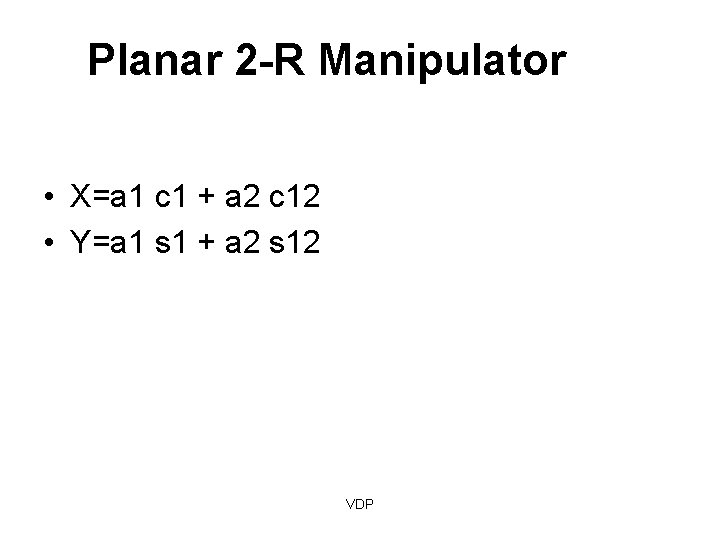
Planar 2 -R Manipulator VDP

Planar 2 -R Manipulator • X=a 1 c 1 + a 2 c 12 • Y=a 1 s 1 + a 2 s 12 VDP

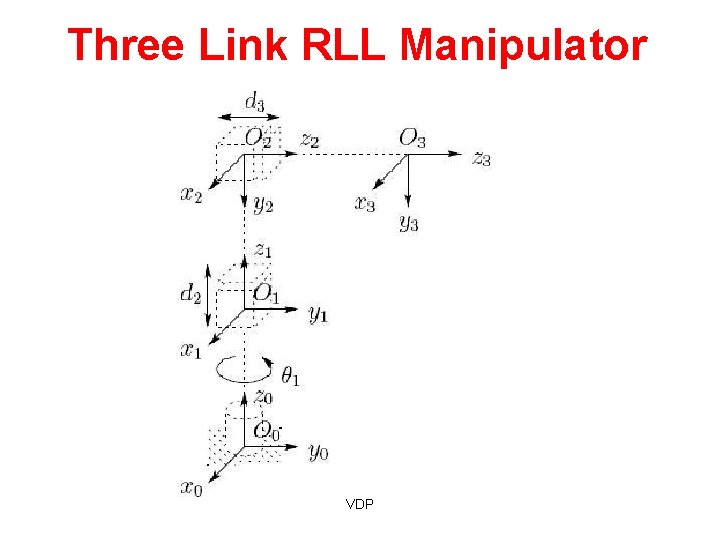
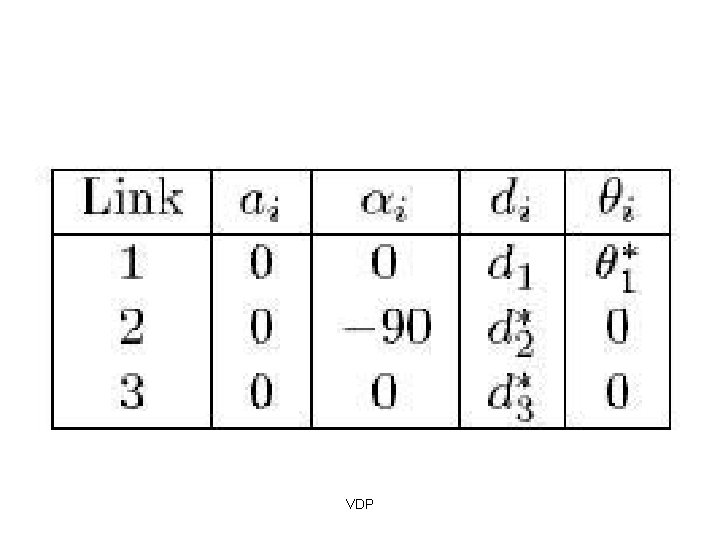
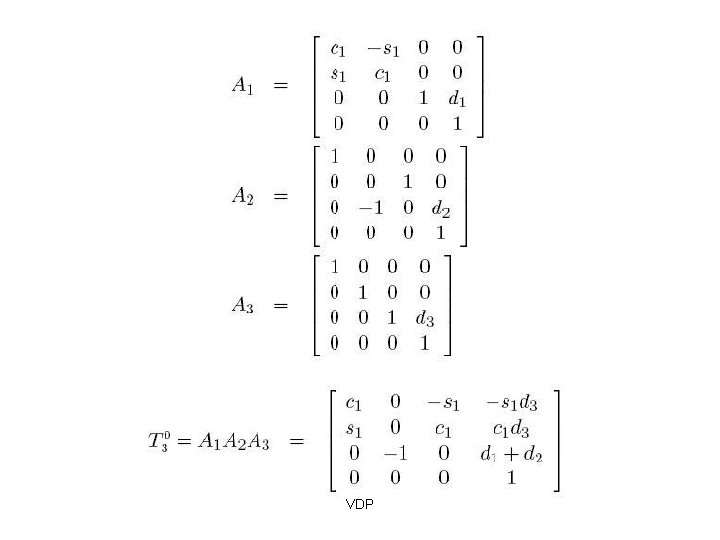
Three Link RLL Manipulator VDP

VDP

VDP
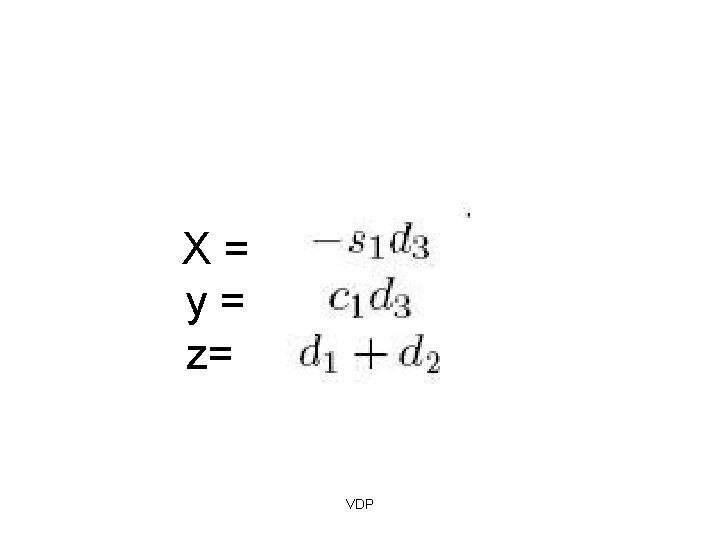
X= y= z= VDP

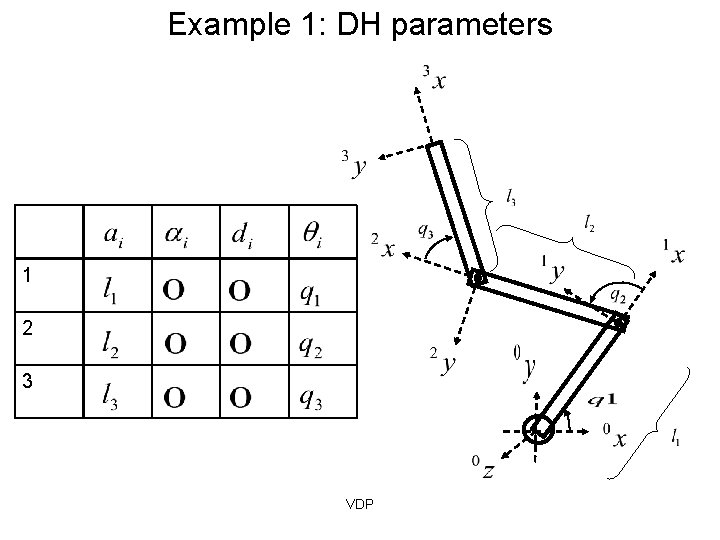
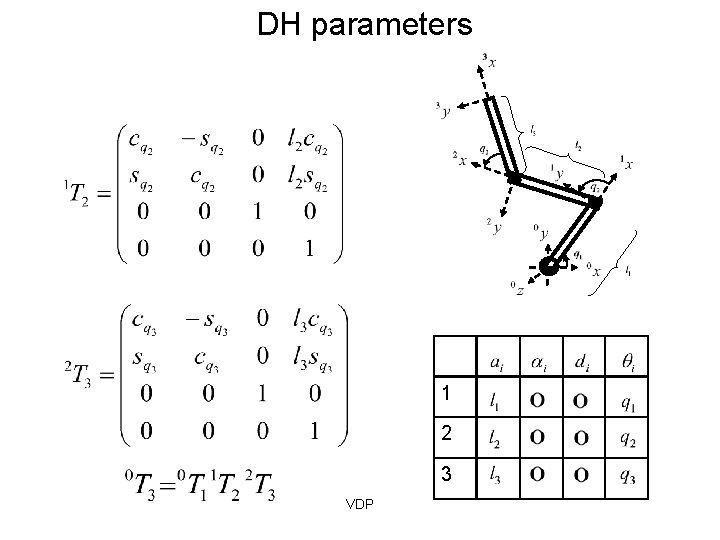
Example 1: DH parameters 1 2 3 VDP

VDP

DH parameters 1 2 3 VDP

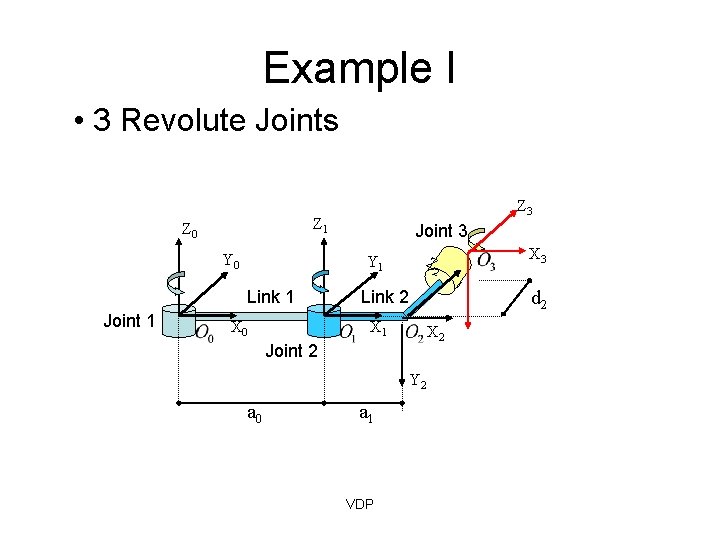
Example I • 3 Revolute Joints Z 1 Z 0 Y 0 Joint 3 Z Y 1 Link 1 Joint 1 Z 3 X 0 2 X 2 Joint 2 Y 2 a 0 d 2 Link 2 X 1 a 1 VDP X 3

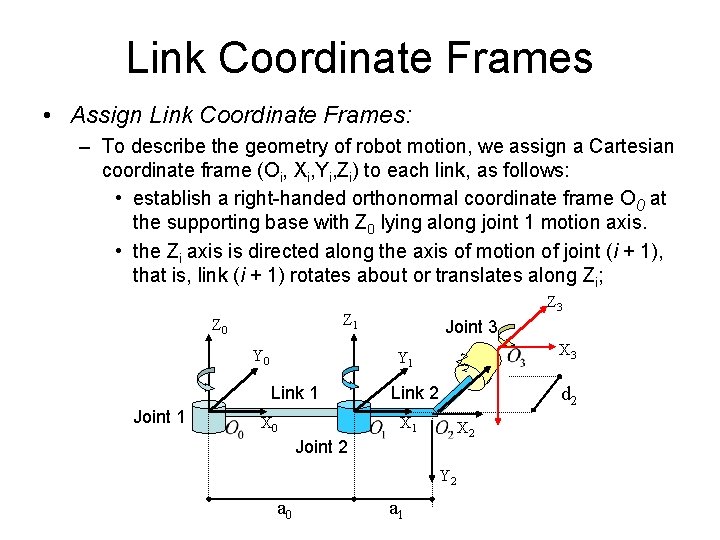
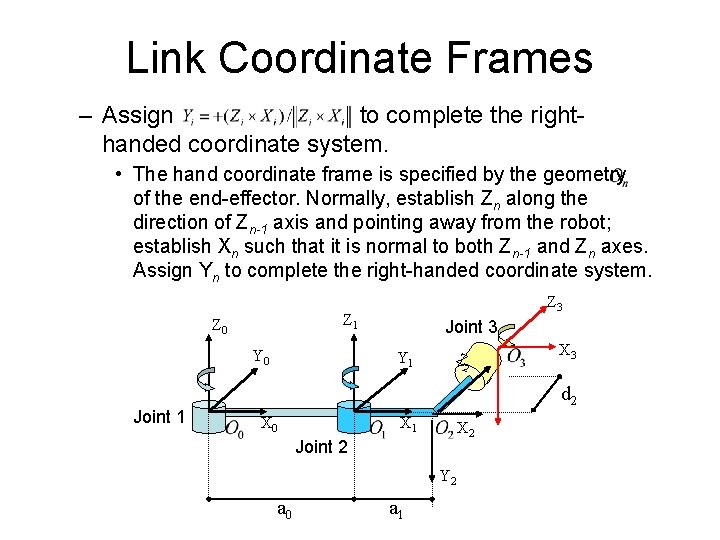
Link Coordinate Frames • Assign Link Coordinate Frames: – To describe the geometry of robot motion, we assign a Cartesian coordinate frame (Oi, Xi, Yi, Zi) to each link, as follows: • establish a right-handed orthonormal coordinate frame O 0 at the supporting base with Z 0 lying along joint 1 motion axis. • the Zi axis is directed along the axis of motion of joint (i + 1), that is, link (i + 1) rotates about or translates along Zi; Z 1 Z 0 Y 0 Joint 3 Z Y 1 Link 1 Joint 1 Z 3 X 0 2 X 2 Joint 2 Y 2 a 0 d 2 Link 2 X 1 a 1 X 3

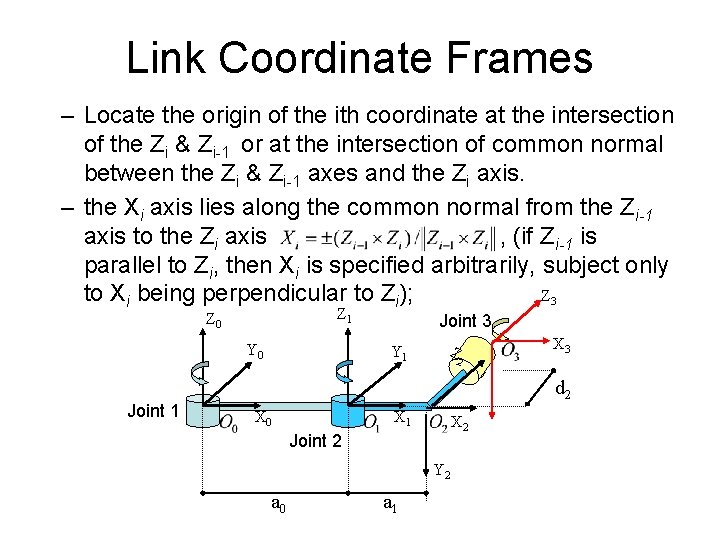
Link Coordinate Frames – Locate the origin of the ith coordinate at the intersection of the Zi & Zi-1 or at the intersection of common normal between the Zi & Zi-1 axes and the Zi axis. – the Xi axis lies along the common normal from the Zi-1 axis to the Zi axis , (if Z i-1 is parallel to Zi, then Xi is specified arbitrarily, subject only Z 3 to Xi being perpendicular to Zi); Z 1 Z 0 Y 0 Joint 1 Joint 3 Y 1 Z 2 X 3 d 2 X 0 X 1 X 2 Joint 2 Y 2 a 0 a 1

Link Coordinate Frames – Assign to complete the righthanded coordinate system. • The hand coordinate frame is specified by the geometry of the end-effector. Normally, establish Zn along the direction of Zn-1 axis and pointing away from the robot; establish Xn such that it is normal to both Zn-1 and Zn axes. Assign Yn to complete the right-handed coordinate system. Z 1 Z 0 Y 0 Joint 1 Z 3 Joint 3 Y 1 Z 2 X 3 d 2 X 0 X 1 X 2 Joint 2 Y 2 a 0 a 1

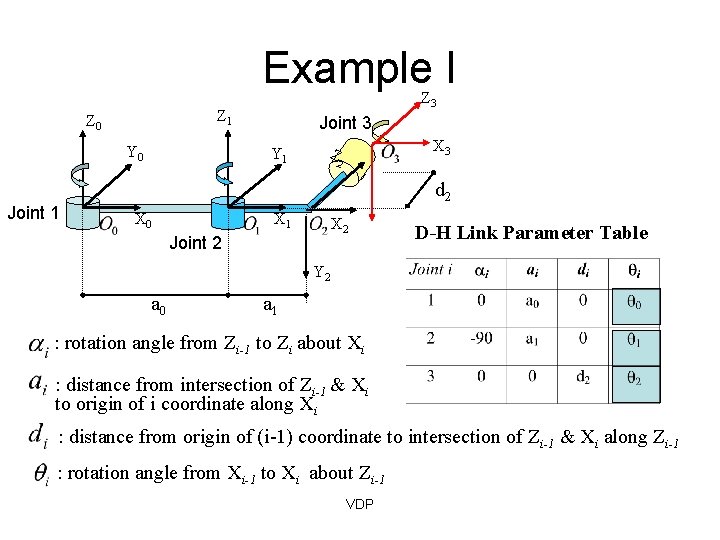
Link and Joint Parameters • Joint angle : the angle of rotation from the Xi-1 axis to the Xi axis about the Zi-1 axis. It is the joint variable if joint i is rotary. • Joint distance : the distance from the origin of the (i-1) coordinate system to the intersection of the Zi-1 axis and the Xi axis along the Zi-1 axis. It is the joint variable if joint i is prismatic. • Link length : the distance from the intersection of the Zi-1 axis and the Xi axis to the origin of the ith coordinate system along the Xi axis. • Link twist angle : the angle of rotation from the Zi-1 axis to the Zi axis about the Xi axis.

Example I Z 1 Z 0 Y 0 Joint 1 Z 3 Joint 3 Y 1 X 3 Z 2 d 2 X 0 X 1 X 2 Joint 2 D-H Link Parameter Table Y 2 a 0 a 1 : rotation angle from Zi-1 to Zi about Xi : distance from intersection of Zi-1 & Xi to origin of i coordinate along Xi : distance from origin of (i-1) coordinate to intersection of Zi-1 & Xi along Zi-1 : rotation angle from Xi-1 to Xi about Zi-1 VDP

Example

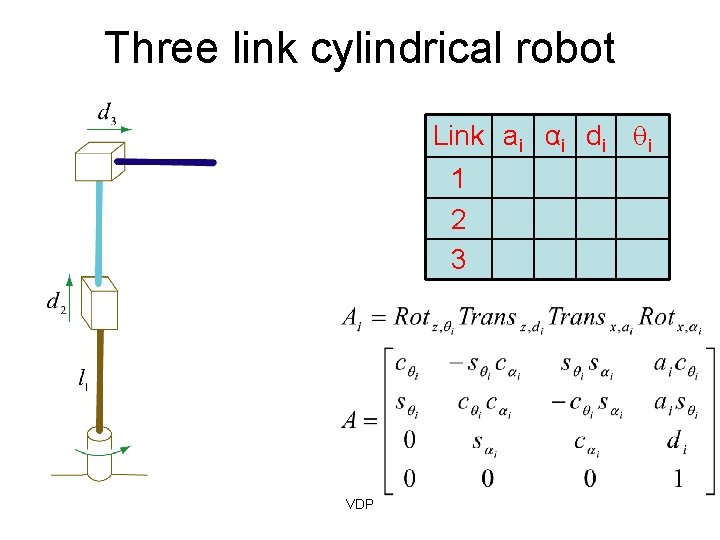
Three link cylindrical robot Link ai αi di i 1 2 3 VDP

VDP

VDP

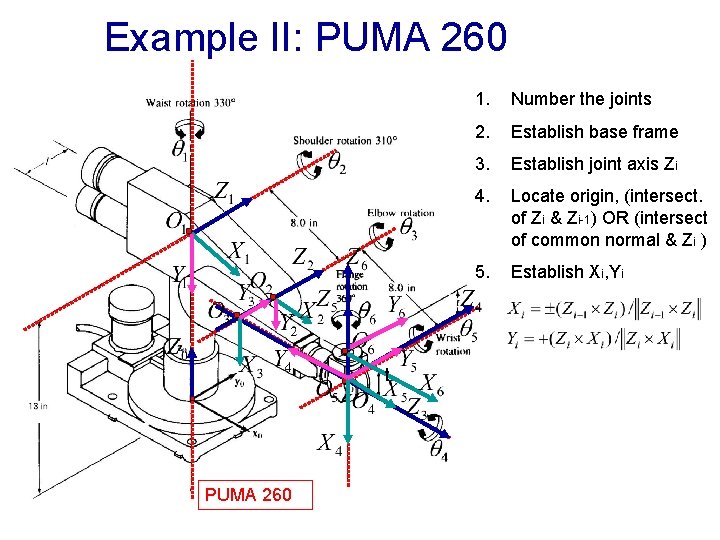
Example II: PUMA 260 t PUMA 260 1. Number the joints 2. Establish base frame 3. Establish joint axis Zi 4. Locate origin, (intersect. of Zi & Zi-1) OR (intersect of common normal & Zi ) 5. Establish Xi, Yi

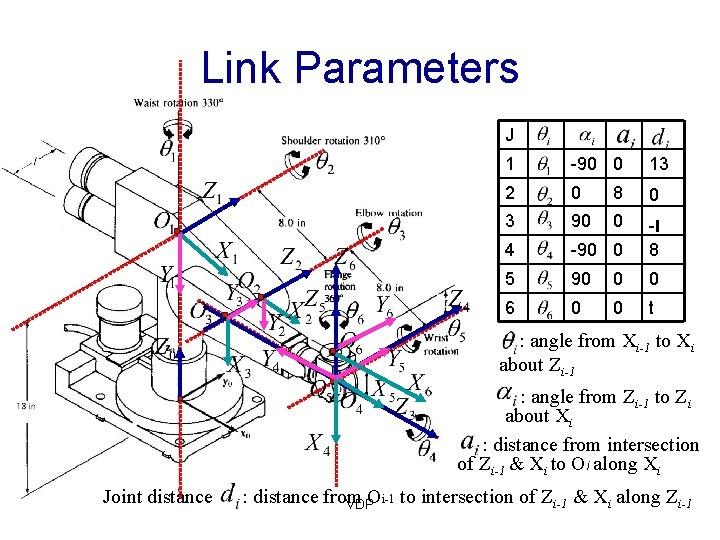
Link Parameters J 1 -90 0 13 2 0 8 0 3 90 0 4 -90 0 -l 8 5 90 0 0 6 0 0 t : angle from Xi-1 to Xi about Zi-1 : angle from Zi-1 to Zi about Xi : distance from intersection of Zi-1 & Xi to Oi along Xi Joint distance : distance from Oi-1 to intersection of Zi-1 & Xi along Zi-1 VDP

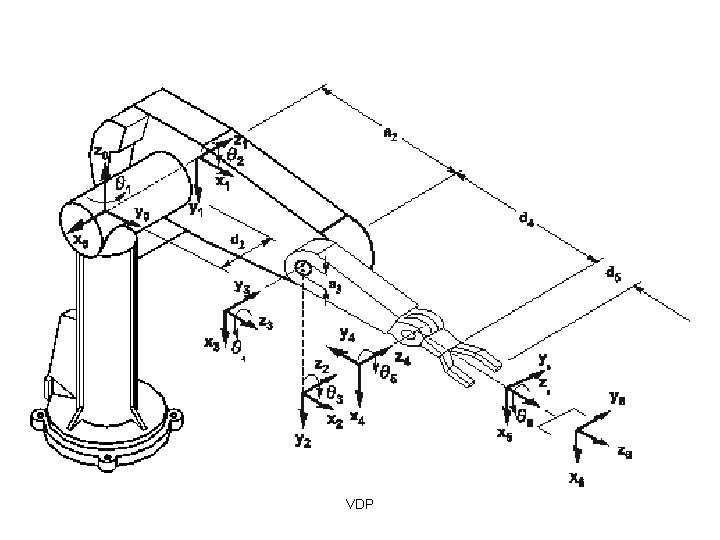
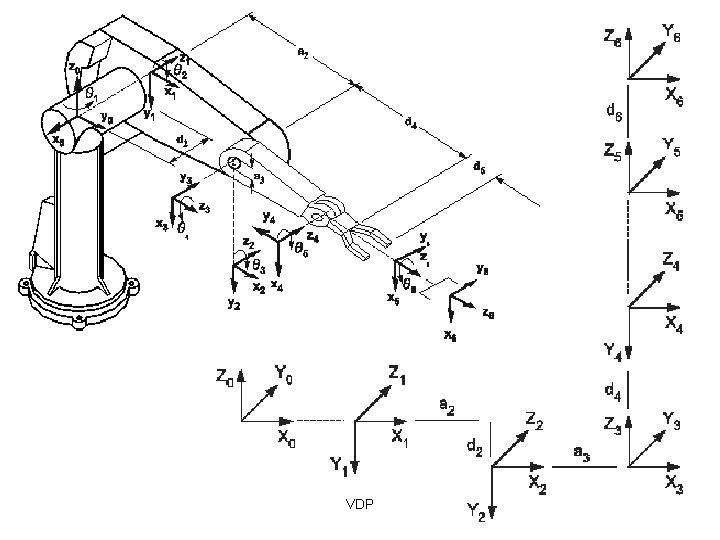
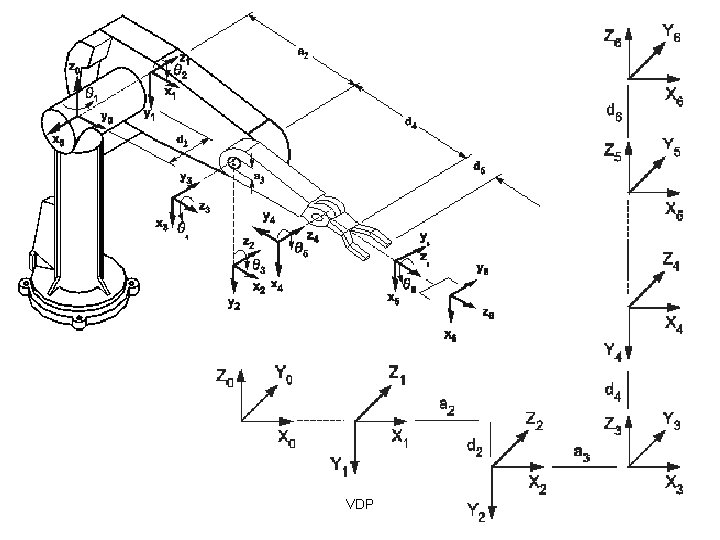
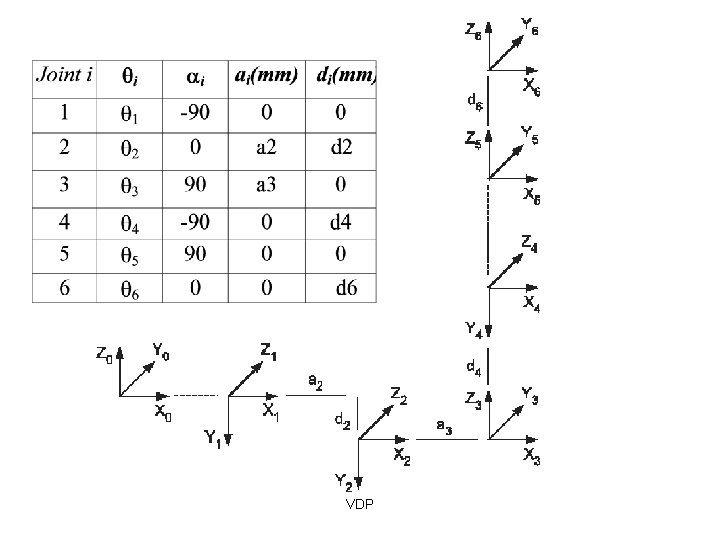
Example: Puma 560 VDP

VDP

VDP

VDP

VDP

VDP

VDP
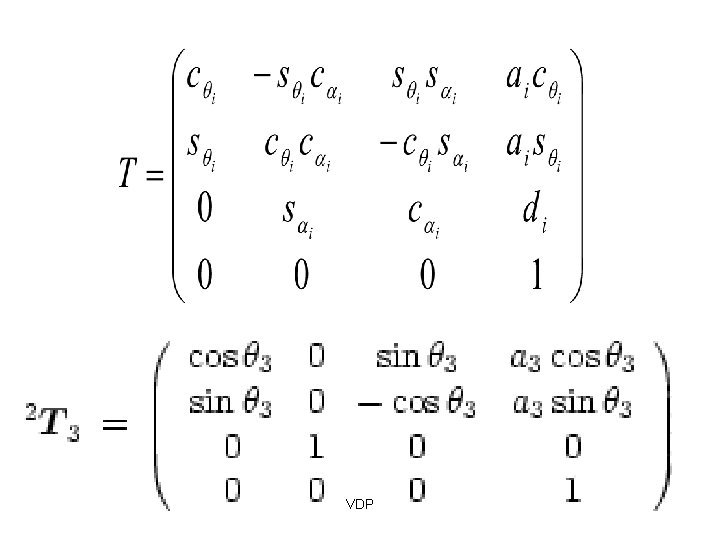
VDP

VDP
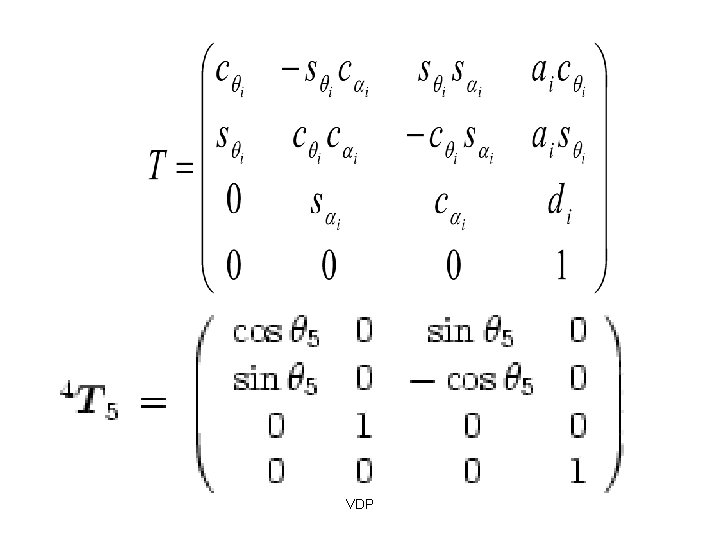
VDP
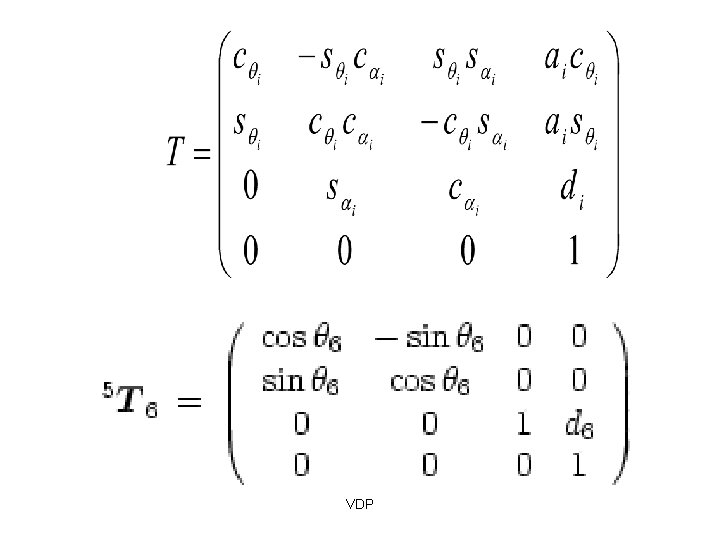
VDP

VDP
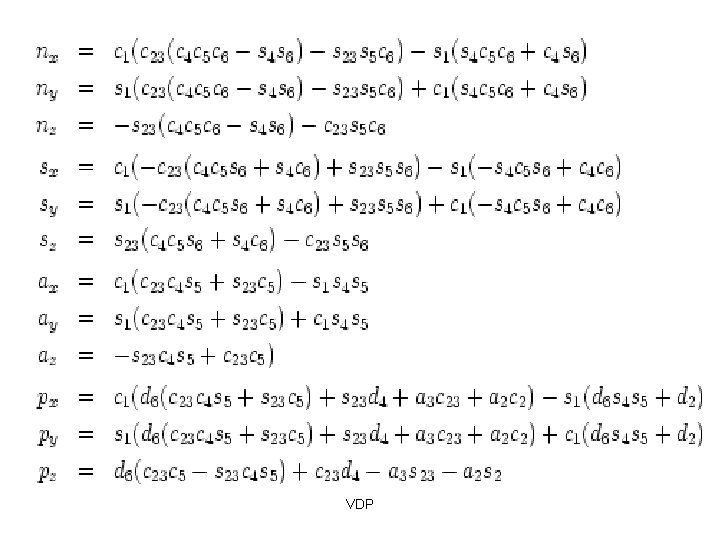
VDP