CHAPTER 4 APPROXIMATE SOLUTION OF NONLINEAR DIFFERENTIAL EQUATIONS






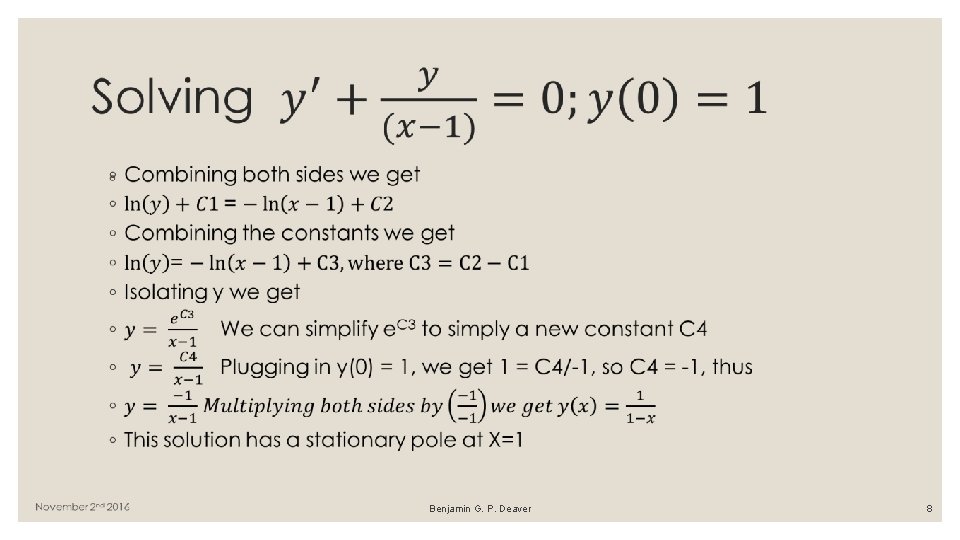







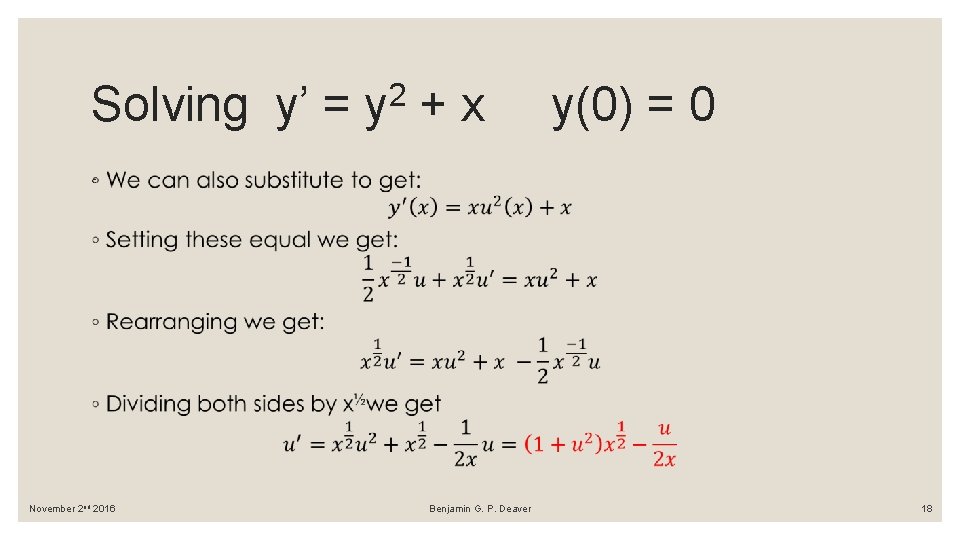



- Slides: 21

CHAPTER 4: APPROXIMATE SOLUTION OF NON-LINEAR DIFFERENTIAL EQUATIONS Sections 4. 1 and 4. 2 Benjamin Deaver

Agenda Section 4. 1 – Spontaneous Singularities ◦ Difference b/w Linear and Non Linear Equations & Definitions ◦ Definition of Singularities & Poles ◦ Fixed vs spontaneous Singularities ◦ Example 1, A and B Section 4. 2 – Approximate Solution of 1 st Order Non-Linear Differential Equations ◦ Infinite spontaneous singularities ◦ Example 2 ◦ Summary November 2 nd 2016 Benjamin G. P. Deaver 2

Non-Linear Differential Equation Non-linear differential equations are those where the dependent variable or its derivatives are at a power different than 1 Linear Differential equations Non-linear differential equations ◦ Y” + xy’ + 2 xy = 14 x ◦ Y” + 3 y’ + xy 2 = 0 ◦ Y” + 14 Y’ + y = 0 ◦ Y” + 3 y’y + xy = 14 ◦ Y” + xy’ = sin(x) ◦ Y” + xy’ = sin(y) ◦ Y” + y = 1/x ◦ Y” + 3 xy’ 2 = 0 Benjamin G. P. Deaver 3

Singularities and Poles ◦ Singularity points – a point at which a function f(X) is undefined or infinite, specifically where f’(x) does not exist. ◦ If a point is not a singular point it is called an ordinary point. ◦ Poles – Are a type of singularity that can be represented in the form F(z) = g(z) / (z-zo)n N is a positive integer referred to as the “order” of the pole g(z) is analytic at zo, and f(zo) ≠ 0 F(z) = (12 z – 4) / ((z-3)2(z+1)) has a 2 nd order pole at z=3 and a simple pole at z =-1 Benjamin G. P. Deaver 4

Fixed vs. Spontaneous singularities Solutions to Non-Linear Differential Equations have more complex singularities than Linear Differential Equations Fixed singularities Spontaneous or movable singularities The location of singularities are independent of the initial condition & only depend on the singularities of the coefficients. The location of singularities move around the plane dependent on initial conditions. For Example: Y’’ + p(t)y’ + g(t)y = 0, Y’’ + (1/t-1)y’ + 3 y = 0, then p(t) will influence the location of the singularities. Benjamin G. P. Deaver 5

Example 1 A: "Linear" fixed singularity ◦ Benjamin G. P. Deaver 6

◦ Benjamin G. P. Deaver 7
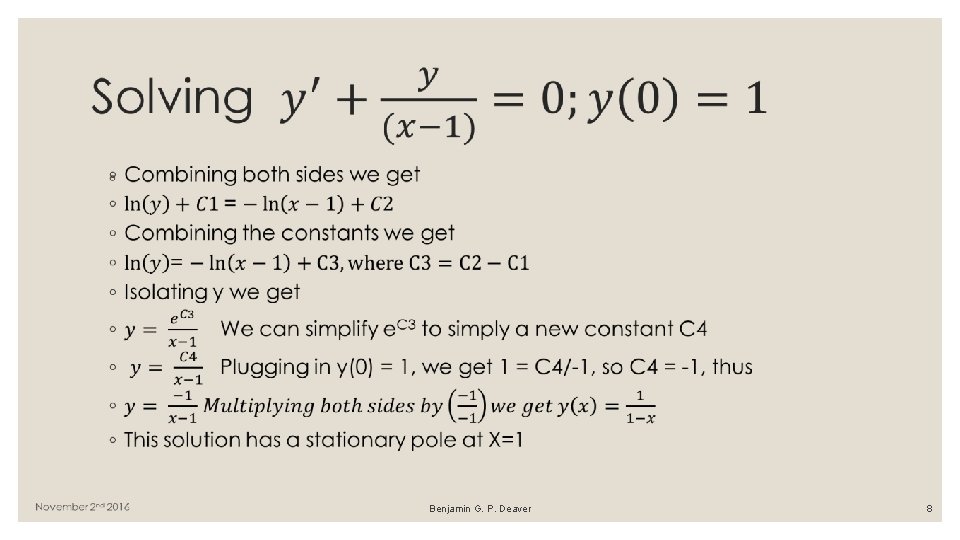
Benjamin G. P. Deaver 8

2 2/12/2022 Benjamin G. P. Deaver 9

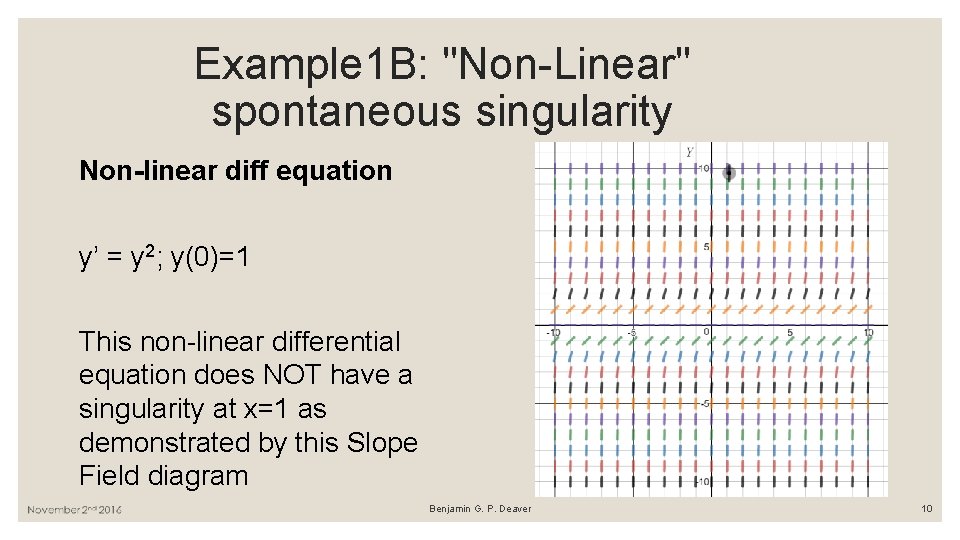
Example 1 B: "Non-Linear" spontaneous singularity Non-linear diff equation y’ = y 2; y(0)=1 This non-linear differential equation does NOT have a singularity at x=1 as demonstrated by this Slope Field diagram Benjamin G. P. Deaver 10

Solving y’ = 2 y; y(0)=1 ◦ Benjamin G. P. Deaver 11

Solving y’ = 2 y; y(0)=1 Benjamin G. P. Deaver 12

Solving y’ = 2 y; y(0)=2 Benjamin G. P. Deaver 13

Infinite Spontaneous Singularities ◦ Benjamin G. P. Deaver 14

Infinite Spontaneous Singularity Example 2: ◦ 2/12/2022 Benjamin G. P. Deaver 15

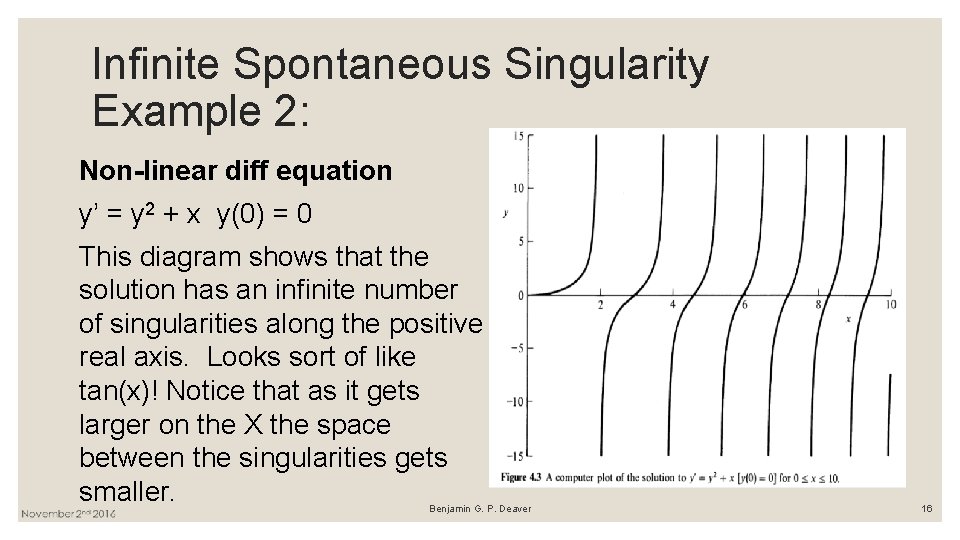
Infinite Spontaneous Singularity Example 2: Non-linear diff equation y’ = y 2 + x y(0) = 0 This diagram shows that the solution has an infinite number of singularities along the positive real axis. Looks sort of like tan(x)! Notice that as it gets larger on the X the space between the singularities gets smaller. Benjamin G. P. Deaver 16

Solving y’ = 2 y + x y(0) = 0 We are now going to have to face this BEAR of a DE here. Luckily our friend “ The Book” had a clever substitution for us to use. November 2 nd 2016 Benjamin G. P. Deaver 17
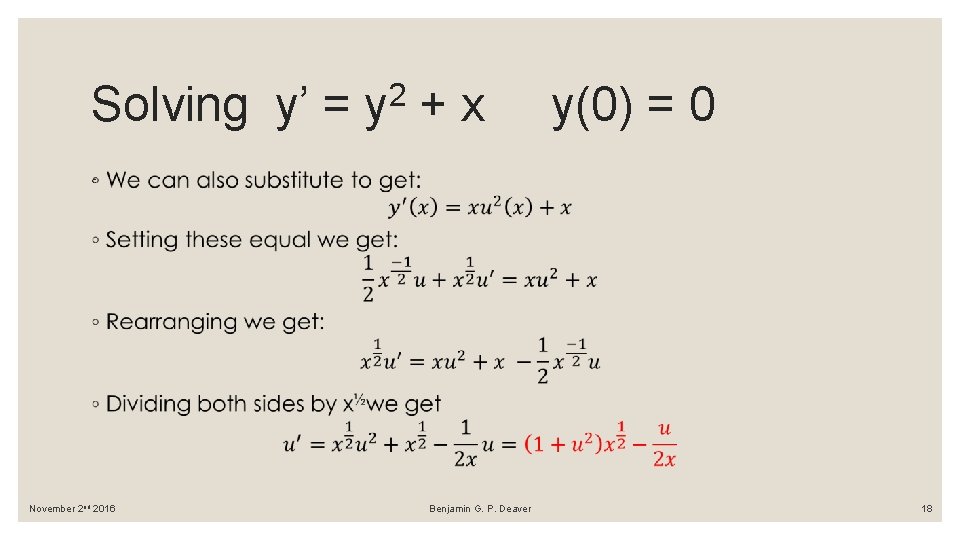
Solving y’ = 2 y +x y(0) = 0 ◦ November 2 nd 2016 Benjamin G. P. Deaver 18

Solving y’ = 2 y +x y(0) = 0 As x-> infinity November 2 nd 2016 Benjamin G. P. Deaver 19

Solving y’ = y 2 + x y(0) = 0 ◦ 2/12/2022 Benjamin G. P. Deaver 20

Summary ◦ Whew! What have we learned? ? ? ◦ First, we learned that the solutions for Non-Linear Differential Equations have UNPREDICTABLE BEHAVIORS. ◦ Next, we have learned that Non-Linear Differential Equations not only have FIXED Singularities, but they also have SPONTANEOUS or MOVABLE Singularities which are Singularities which move around the plane as the initial conditions change. ◦ Then, we learned that it is DIFFICULT to ANALYTICALLY SOLVE Non-Linear Differential Equations. ◦ Finally, we learned a few techniques for APPROXIMATING the solutions of First Order Non-Linear Differential Equations. These approximations include: ◦ Approximations at Infinity, where terms can be ignored to simplify the differential equation. ◦ Substitutions which enable the differential equation to become separable and solvable. November 2 nd 2016 Benjamin G. P. Deaver 21
 Nonlinear ordinary differential equation
Nonlinear ordinary differential equation Solution of nonlinear equations by bisection method
Solution of nonlinear equations by bisection method Kutta
Kutta Ode in maths
Ode in maths Natural solution
Natural solution Differential equations chapter 1
Differential equations chapter 1 Graphing systems of nonlinear equations
Graphing systems of nonlinear equations Linear vs nonlinear table
Linear vs nonlinear table Differences between linear and nonlinear equations
Differences between linear and nonlinear equations Nonlinear systems of equations worksheet
Nonlinear systems of equations worksheet Nonlinear equations
Nonlinear equations Non linear simultaneous equations
Non linear simultaneous equations Non linear simultaneous equations
Non linear simultaneous equations Nonlinear equations
Nonlinear equations Secant method nonlinear equations
Secant method nonlinear equations Pde solutions
Pde solutions Differential equation exponential solution
Differential equation exponential solution Find the general solution of the differential equation
Find the general solution of the differential equation What is a first order equation
What is a first order equation First ode
First ode General form of bessel equation
General form of bessel equation Logistic differential equation solution
Logistic differential equation solution







































