Central Limit Theorem Section 5 5 M A

  • Slides: 20
Download presentation
Central Limit Theorem Section 5 -5 M A R I O F. T R

Central Limit Theorem Section 5 -5 M A R I O F. T R I O L A Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 1

As the sample size increases the distribution of sample means will approach a normal

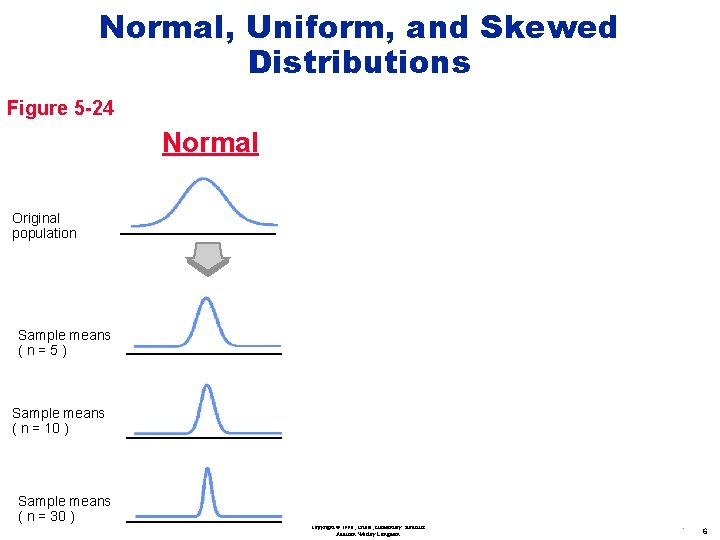
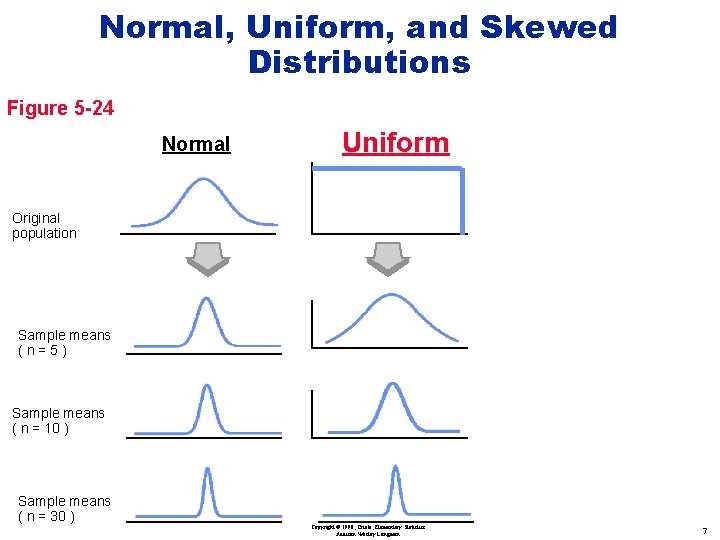
As the sample size increases the distribution of sample means will approach a normal distribution. Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 2

Distribution of 200 digits From Social Security Numbers Frequency (Last 4 digits from 50

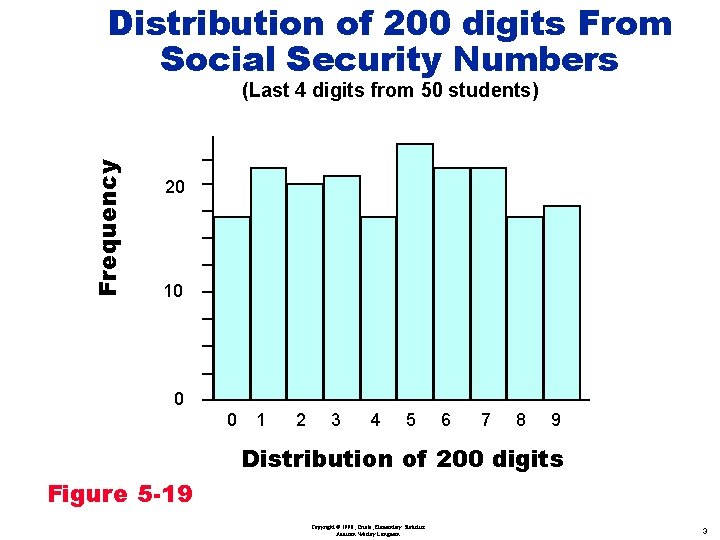
Distribution of 200 digits From Social Security Numbers Frequency (Last 4 digits from 50 students) 20 10 0 0 1 2 3 4 5 6 7 8 9 Distribution of 200 digits Figure 5 -19 Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 3

Table 5 -1 x SSN digits 1 5 9 4 7 9 5 7

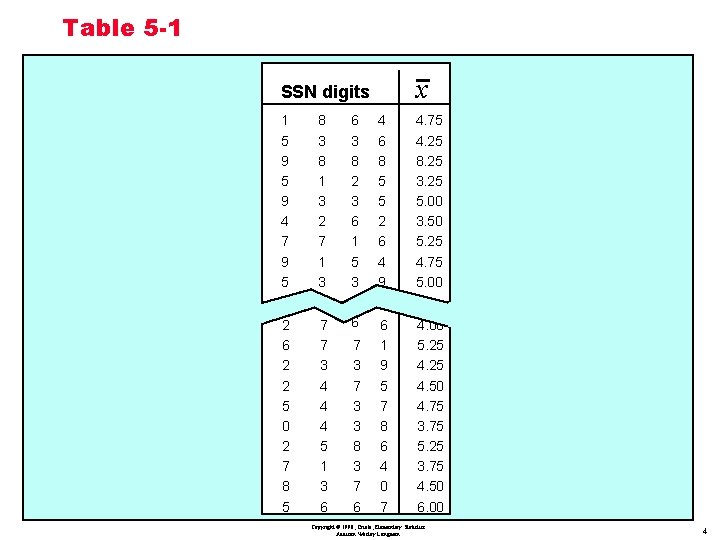
Table 5 -1 x SSN digits 1 5 9 4 7 9 5 7 8 3 8 1 3 2 7 1 3 83 2 6 2 2 5 0 2 7 8 5 7 7 3 4 4 4 5 1 3 6 6 3 8 2 3 6 1 5 3 42 6 7 3 3 8 3 7 6 4 6 8 5 5 2 6 4 9 4. 75 4. 25 8. 25 3. 25 5. 00 3. 50 5. 25 4. 75 5. 00 2 6 1 9 5 7 8 6 4 0 7 4. 00 5. 25 4. 50 4. 75 3. 75 5. 25 3. 75 4. 50 6. 00 Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 4

Frequency Distribution of 50 Sample Means for Students 15 10 5 0 0 1

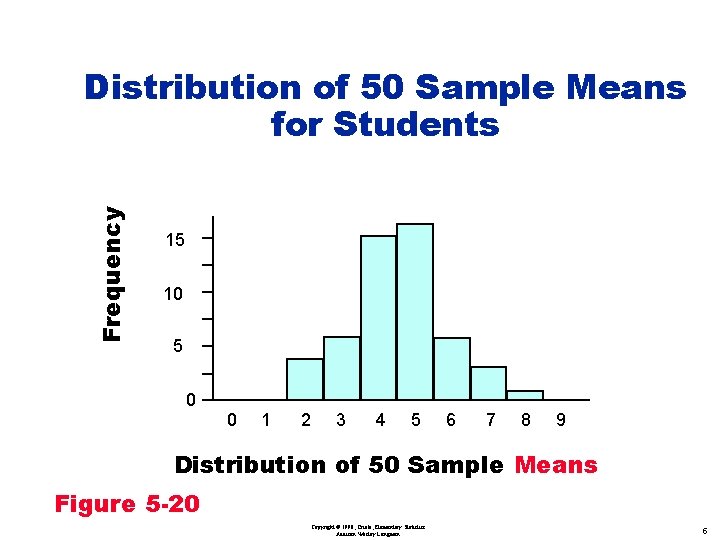
Frequency Distribution of 50 Sample Means for Students 15 10 5 0 0 1 2 3 4 5 6 7 8 9 Distribution of 50 Sample Means Figure 5 -20 Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 5

Normal, Uniform, and Skewed Distributions Figure 5 -24 Normal Uniform Skewed Original population Sample

Normal, Uniform, and Skewed Distributions Figure 5 -24 Normal Uniform Skewed Original population Sample means (n=5) Sample means ( n = 10 ) Sample means ( n = 30 ) Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 6

Normal, Uniform, and Skewed Distributions Figure 5 -24 Normal Uniform Original population Sample means

Normal, Uniform, and Skewed Distributions Figure 5 -24 Normal Uniform Original population Sample means (n=5) Sample means ( n = 10 ) Sample means ( n = 30 ) Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 7

Normal, Uniform, and Skewed Distributions Figure 5 -24 Normal Uniform Skewed Original population Sample

Normal, Uniform, and Skewed Distributions Figure 5 -24 Normal Uniform Skewed Original population Sample means (n=5) Sample means ( n = 10 ) Sample means ( n = 30 ) Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 8

Central Limit Theorem Given: 1. The random variable x has a distribution (which may

Central Limit Theorem Given: 1. The random variable x has a distribution (which may or may not be normal) with mean µ and standard deviation s. 2. Samples of size population. n are randomly selected from this Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 9

Central Limit Theorem Given: 1. The random variable x has a distribution (which may

Central Limit Theorem Given: 1. The random variable x has a distribution (which may or may not be normal) with mean µ and standard deviation s. 2. Samples of size population. n are randomly selected from this Conclusions: Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 10

Central Limit Theorem Given: 1. The random variable x has a distribution (which may

Central Limit Theorem Given: 1. The random variable x has a distribution (which may or may not be normal) with mean µ and standard deviation s. 2. Samples of size population. n are randomly selected from this Conclusions: 1. The distribution of sample means x will, as the sample size increases, approach a normal distribution. Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 11

Central Limit Theorem Given: 1. The random variable x has a distribution (which may

Central Limit Theorem Given: 1. The random variable x has a distribution (which may or may not be normal) with mean µ and standard deviation s. 2. Samples of size population. n are randomly selected from this Conclusions: 1. The distribution of sample means x will, as the sample size increases, approach a normal distribution. 2. The mean of the sample means will be the population mean µ. s 3. The standard deviation of the sample means will be — n Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 12

Practical Rules Commonly Used : 1. For samples of size n larger than 30,

Practical Rules Commonly Used : 1. For samples of size n larger than 30, the distribution of the sample means can be approximated reasonably well by a normal distribution. The approximation gets better as the sample size n becomes larger. 2. If the original population is itself normally distributed, then the sample means will be normally distributed for any sample size n. Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 13

Notation Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 14

Notation Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 14

Notation the mean of the sample means µx = µ the standard deviation of

Notation the mean of the sample means µx = µ the standard deviation of sample mean sx = s n (often called standard error of the mean) Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 15

Notation the mean of the sample means µx = µ the standard deviation of

Notation the mean of the sample means µx = µ the standard deviation of sample means sx = s n (often called standard error of the mean) Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 16

Notation the mean of the sample means µx = µ the standard deviation of

Notation the mean of the sample means µx = µ the standard deviation of sample mean sx = s n (often called standard error of the mean) Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 17

Sampling Without Replacement If n > 0. 05 N Copyright © 1998, Triola, Elementary

Sampling Without Replacement If n > 0. 05 N Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 18

Sampling Without Replacement If n > 0. 05 N s sx = n N–

Sampling Without Replacement If n > 0. 05 N s sx = n N– 1 Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 19

Sampling Without Replacement If n > 0. 05 N s sx = n N–

Sampling Without Replacement If n > 0. 05 N s sx = n N– 1 finite population correction factor Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 20

Central limit theorem outlines Central limit theorem CLTCentral limit theorem outlines Central limit theorem CLT
Central Limit Theorem The central limit theorem andCentral Limit Theorem The central limit theorem and
Central limit theorem outlines Central limit theorem CLTCentral limit theorem outlines Central limit theorem CLT
Central Limit Theorem The theorem states that theCentral Limit Theorem The theorem states that the
LIMIT FUNGSI ALJABAR Limit fungsi aljabar LIMIT FUNGSILIMIT FUNGSI ALJABAR Limit fungsi aljabar LIMIT FUNGSI
Limit Sets Limit Sets Defined Limit Sets groupsLimit Sets Limit Sets Defined Limit Sets groups
LIMIT FUNGSI LIMIT FUNGSI PENGERTIAN LIMIT Perhatikan fungsiLIMIT FUNGSI LIMIT FUNGSI PENGERTIAN LIMIT Perhatikan fungsi
Limit MATHEMATICS LIMIT CRASH COURSE Limit of aLimit MATHEMATICS LIMIT CRASH COURSE Limit of a
limit Limit f limit f 0limit f xlimit Limit f limit f 0limit f x
Central Limit Theorem l Sampling Distributions l CentralCentral Limit Theorem l Sampling Distributions l Central
Ch 7 Central Limit Theorem Use the CentralCh 7 Central Limit Theorem Use the Central
Section 6 5 The Central Limit Theorem LearningSection 6 5 The Central Limit Theorem Learning
Section 6 5 The Central Limit Theorem DistributionSection 6 5 The Central Limit Theorem Distribution
The Central Limit Theorem Section 9 3 2The Central Limit Theorem Section 9 3 2
Section 6 5 The Central Limit Theorem THESection 6 5 The Central Limit Theorem THE
SHAPE SPACE Pythagorean Theorem Pythagorean Theorem Pythagorean TheoremSHAPE SPACE Pythagorean Theorem Pythagorean Theorem Pythagorean Theorem
LEMIs Theorem Lamis Theorem Statement Lamis theorem isLEMIs Theorem Lamis Theorem Statement Lamis theorem is
VARIGNONS THEOREM What is Varigons Theorem The theoremVARIGNONS THEOREM What is Varigons Theorem The theorem
Thvenins Theorem Thevenins Theorem Thevenins theorem simplifies theThvenins Theorem Thevenins Theorem Thevenins theorem simplifies the