Limit MATHEMATICS LIMIT CRASH COURSE Limit of a
















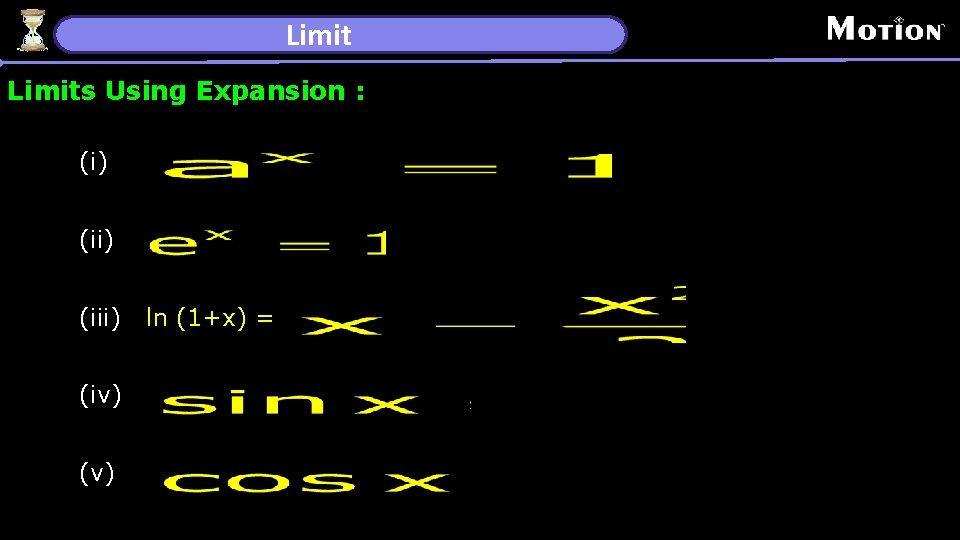










![Question Evaluate Where [ ] denotes the greatest integer function. (A) (B) (C) (D) Question Evaluate Where [ ] denotes the greatest integer function. (A) (B) (C) (D)](https://slidetodoc.com/presentation_image_h2/3e62615b45db55770162e46a816d1fae/image-31.jpg)






![Question For each x Î R, let [x] be the greatest integer less than Question For each x Î R, let [x] be the greatest integer less than](https://slidetodoc.com/presentation_image_h2/3e62615b45db55770162e46a816d1fae/image-38.jpg)




![Question Let [x] denote the greatest integer less than or equal to x. then Question Let [x] denote the greatest integer less than or equal to x. then](https://slidetodoc.com/presentation_image_h2/3e62615b45db55770162e46a816d1fae/image-43.jpg)
![Question If integer function then where [. ] denotes greatest =. . . Question If integer function then where [. ] denotes greatest =. . .](https://slidetodoc.com/presentation_image_h2/3e62615b45db55770162e46a816d1fae/image-44.jpg)




- Slides: 48

Limit MATHEMATICS LIMIT CRASH COURSE

Limit of a function f(x) is said to exist as, x ® a when, f(a - h) (Left hand limit) = f (a + h) = a. f. q (a finite quantity say M). (Right hand limit) = afq Note: # We are not interested in knowing about what happens at x = a. # Also note that if L. H. L. & R. H. L. are both tending towards ' ¥ ' or ‘– ¥’ then it is said to be infinite limit. # Remember, Þ x ¹ a

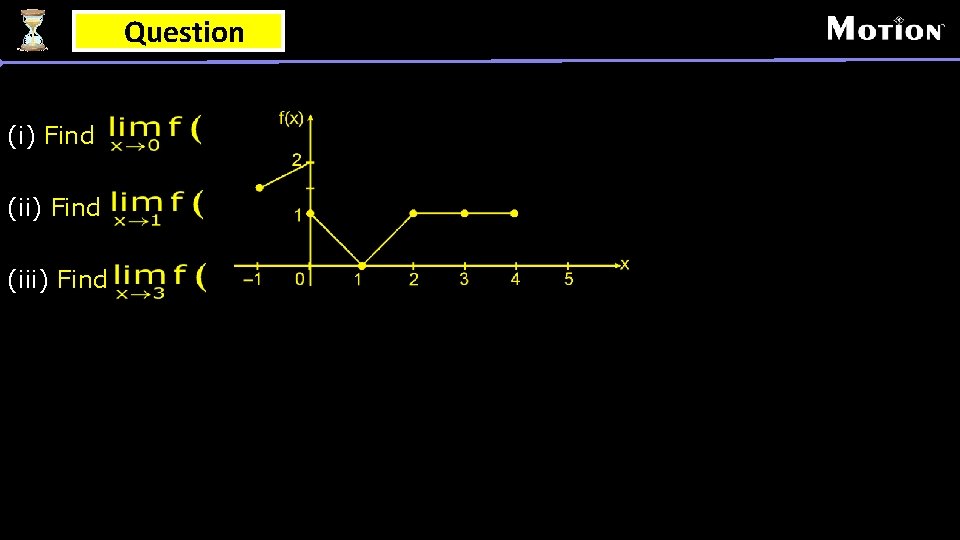
Question (i) Find (iii) Find

Limit Indeterminant Forms: , , 0 × ¥, ¥ - ¥, ¥ 0, 00, and 1¥. Note : (i) ‘ 0‘ doesn't means exact zero but represent a value approaching towards zero similarly to ‘ 1' and infinity. (ii) ¥+¥=¥ (iii) ¥x¥=¥ (iv) (a/ ¥) = 0 (if a is finite)

Limit Method of Removing Indeterminancy : To evaluate a limit, we must always put the value where ‘x' is approaching to in the function. If we get a determinate form, then that value becomes the limit otherwise if an indeterminant form comes then apply one of the following methods: (i) Factorisation (ii) Rationalisation or double rationalisation (iii) Substitution (iv) Using standard limits (v) Expansions of functions.

Limit (i) Factorization Method Indeterminant Forms: We cancel out the factors which are leading to indeterminacy And find the limit of the remaining expression.

Question Evaluate (A)10 (B) 11 (C) 12 (D) 13 :

Limit (ii) Rationalization / Double Rationalization : We can rationalize the irrational expression by multiplying with their conjugates to remove the indeterminancy.

Question Evaluate (A) (B) (C) – 1 (D) 1 :

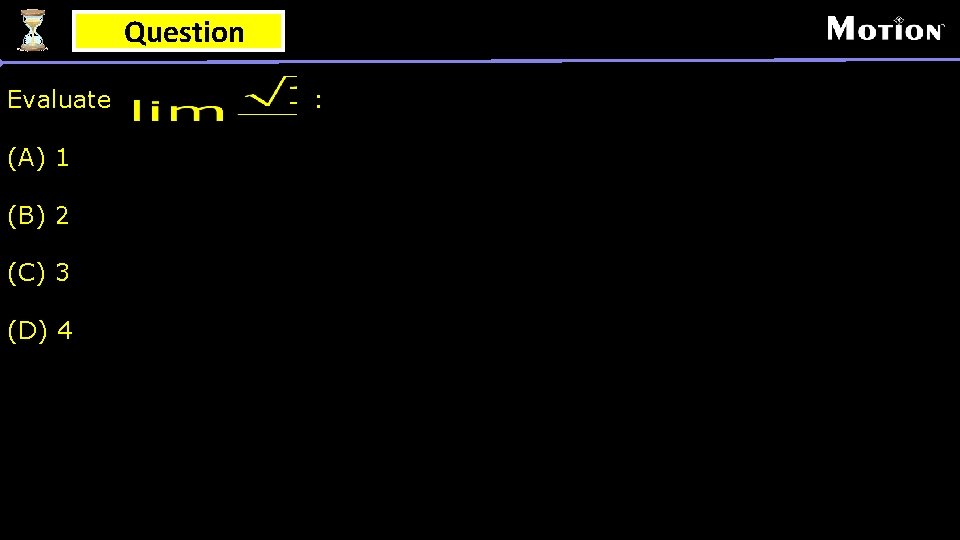
Question Evaluate (A) 1 (B) 2 (C) 3 (D) 4 :

Question Evaluate (A) (B) (C) (D) :

Limit (iii) Fundamental Theorems on Limits : Let f (x) = & g (x) = m. If & m exists, then: (i) {f(x) ± g (x)} = l ± m (ii) {f(x). g(x) } = l. m (iii) = (iv) k f(x) = k (v) f[g(x)] = g(x) = m. , provided m ¹ 0 f(x) ; where k is a constant. = f (m); provided f is continuous at

Limit (iv) Standard Limits : (a) =1= = = [Where x is measured in radians ] (b) (c) (d) (e) (1 + x)1/x = e ; = 1; =1 = nan – 1. =e = logea, a > 0

Question

Question Evaluate (A) 1 (B) 2 (C) 3 (D) 4 :

Limit When x ® ¥ Since x ® ¥ Þ ® 0 hence in this type of problem we express most of the part of expression in terms of and apply ® 0.

Question Evaluate (A) 0 (B) 1 (C) 2 (D) 3 :

Question Evaluate (A) (B) (C) (D) :
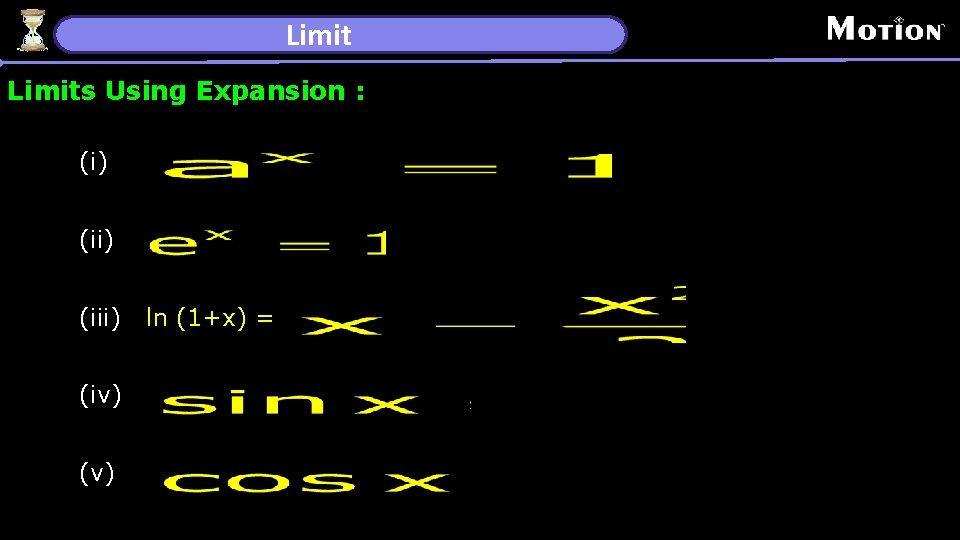
Limits Using Expansion : (i) (iii) (iv) (v) ln (1+x) =

Limit (vi) (viii) ln (1+x) = (ix) (x) for |x| < 1, n Î R (1 + x)n = 1 + nx + + +. . . ¥

Question Evaluate (A) (B) (C) (D) :

Question Evaluate (A) (B) (C) (D) :

Question Evaluate (A) (B) (C) (D) :

Question Evaluate (A) (B) (C) (D) :

Limits of form 1¥, 00, ¥ 0 All these forms can be convered into form in the following ways

Question Evaluate (A) e– 8 (B) e– 1 (C) e 2 (D) e-2/p :

Question Evaluate (A) e– 8 (B) e– 1 (C) e 2 (D) e-2/p :

Question Evaluate (A) e– 8 (B) e– 1 (C) e 2 (D) e-2/p :

Question Evaluate (A) 1 (B) 2 (C) 3 (D) 4 :

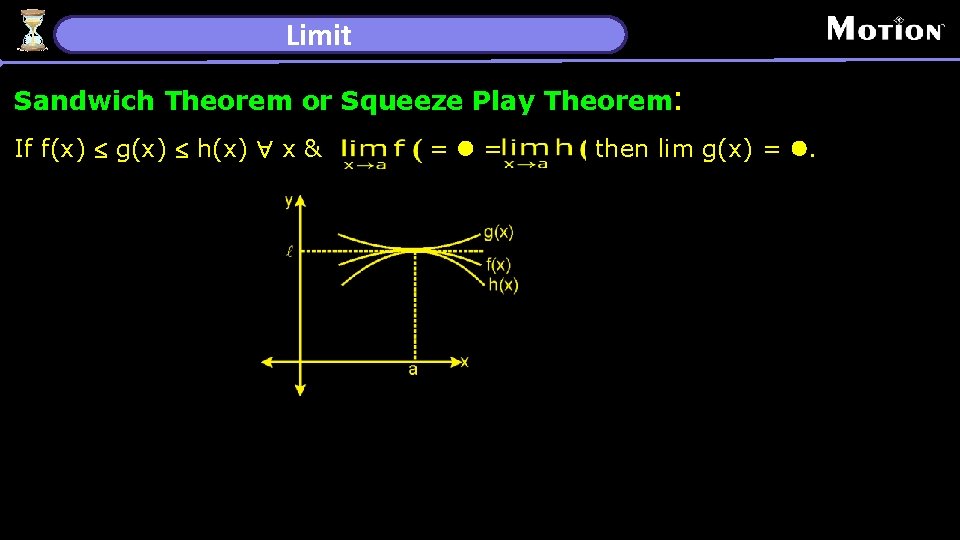
Limit Sandwich Theorem or Squeeze Play Theorem: If f(x) £ g(x) £ h(x) " x & =l= then lim g(x) = l.
![Question Evaluate Where denotes the greatest integer function A B C D Question Evaluate Where [ ] denotes the greatest integer function. (A) (B) (C) (D)](https://slidetodoc.com/presentation_image_h2/3e62615b45db55770162e46a816d1fae/image-31.jpg)
Question Evaluate Where [ ] denotes the greatest integer function. (A) (B) (C) (D)

Question

Limit Some Important Notes (i) : (ii) As x® ¥, ln x increases much slower than any (+ve) power of x where e x increases much faster than (+ve) power of x (iii) (iv) If (1 - h) = 0 & (1 + h)n ® ¥ where h > 0. n f(x) = A > 0 & f (x) = B (a finite quantity) then; [f(x)]f(x) = ez where z = f (x). ln[f(x)] = e. Bin. A = AB

Question Built in Limit Concept:

Question

Question Evaluate (A) 0 (B) 2 (C) 3 (D) 4 :

Question Let f be a differentiable function such that f'(x) = 7 – f(1) ¹ 4. Then (A) exists and equals 0 (B) exists and equals (C) does not exist. (D) exists and equals 4. and
![Question For each x Î R let x be the greatest integer less than Question For each x Î R, let [x] be the greatest integer less than](https://slidetodoc.com/presentation_image_h2/3e62615b45db55770162e46a816d1fae/image-38.jpg)
Question For each x Î R, let [x] be the greatest integer less than or equal to x. Then (A)1 (B) sin 1 (C) – sin 1 (D) 0 is equal to:

Question If then is __

Question Let f(x)= 5 – |x – 2| and g(x) = |x + 1|, x Î R. If f(x) attains maximum value at a and g(x) attains minimum value at b, then is equal to (A) 3/2 (B) – 3/2 (C) – 1/2 (D) 1/2

Question If (A)-7 (B) -4 (C) 1 (D) 5 then a + b is equal to :

Question If (A) (B) (C) (D) , then k is :
![Question Let x denote the greatest integer less than or equal to x then Question Let [x] denote the greatest integer less than or equal to x. then](https://slidetodoc.com/presentation_image_h2/3e62615b45db55770162e46a816d1fae/image-43.jpg)
Question Let [x] denote the greatest integer less than or equal to x. then : (A)does not exist (B) equals 0 (C) equals p + 1 (D) equals p
![Question If integer function then where denotes greatest Question If integer function then where [. ] denotes greatest =. . .](https://slidetodoc.com/presentation_image_h2/3e62615b45db55770162e46a816d1fae/image-44.jpg)
Question If integer function then where [. ] denotes greatest =. . .

Question Let e denote the base of the natural logarithm. The value of the real number for which the right hand limit non-zero real number, is____ is equal to a

Question Let f : R ® R be a differentiable function satisfying f'(3) + f'(2) = 0. Then (A)e 2 (B) 1 (C) e-1 (D) e is equal to:

Question equals: (A) 4 (B) (C) (D)

 Coronary circulation of heart
Coronary circulation of heart Crash course axial skeleton
Crash course axial skeleton Endo epi peri
Endo epi peri Physical chemistry crash course
Physical chemistry crash course Molecular biology crash course
Molecular biology crash course Crash course wwi
Crash course wwi Crash course ancient greece
Crash course ancient greece Crash course hardy weinberg
Crash course hardy weinberg Weathr
Weathr Youtube
Youtube Cold war crash course
Cold war crash course Calculus crash course
Calculus crash course Oliver schulte
Oliver schulte Industrialization crash course
Industrialization crash course Traversy media react native
Traversy media react native The command line crash course
The command line crash course Crash course personality
Crash course personality Unity crash course
Unity crash course Uml crash course
Uml crash course Ap language and composition crash course
Ap language and composition crash course Crash course philosophy existentialism
Crash course philosophy existentialism Weather and climate crash course
Weather and climate crash course Ros crash course
Ros crash course Crash course psychology consciousness
Crash course psychology consciousness Depreciation aspe
Depreciation aspe Phylogenetic tree grade 11
Phylogenetic tree grade 11 Lsn in dbms
Lsn in dbms Project management crash course
Project management crash course The crucible crash course
The crucible crash course Crash course sliding filament theory
Crash course sliding filament theory Gas laws crash course
Gas laws crash course Crash course muscles part 2
Crash course muscles part 2 Crash course protestant reformation
Crash course protestant reformation Computer architecture crash course
Computer architecture crash course Cognitive psychology crash course
Cognitive psychology crash course What example does hank green give for social loafing?
What example does hank green give for social loafing? Robotics crash course
Robotics crash course Crash course harlem renaissance
Crash course harlem renaissance Woo hoo
Woo hoo Meth eth prop but pent table
Meth eth prop but pent table English grammar crash course
English grammar crash course Data mining crash course
Data mining crash course Crusades crash course
Crusades crash course Aerobic respiration crash course
Aerobic respiration crash course Crash course test anxiety
Crash course test anxiety Alabama course of study math
Alabama course of study math Limites de control
Limites de control Cara menggambar grafik limit
Cara menggambar grafik limit Upper specification limit and lower specification limit
Upper specification limit and lower specification limit