Section 6 5 The Central Limit Theorem Learning

  • Slides: 30
Download presentation
Section 6. 5 The Central Limit Theorem

Section 6. 5 The Central Limit Theorem

Learning Targets The Central Limit Theorem tells us that for a population with any

Learning Targets The Central Limit Theorem tells us that for a population with any distribution, the distribution of the sample means approaches a normal distribution as the sample size increases. The procedure in this section form the foundation for estimating population parameters and hypothesis testing.

Given 1. 2. The random variable X has a distribution (which may or may

Given 1. 2. The random variable X has a distribution (which may or may not be normal) with mean and standard deviation . Simple random samples all of the same size n are selected from the population. (The samples are selected so that all possible samples of the same size n have the same chance of being selected. )

Conclusions

Conclusions

Practical Rules Commonly Used 1. 2. For a population with any distribution, if n

Practical Rules Commonly Used 1. 2. For a population with any distribution, if n > 30, then the distribution of the sample means can be approximated reasonably well by a normal distribution. The approximation gets closer to a normal distribution as the sample size n becomes larger. If the original population is normally distributed, then for any sample size n, the sample means will be normally distributed.

Practical Rules Commonly Used 3. If n ≤ 30 and the original distribution does

Practical Rules Commonly Used 3. If n ≤ 30 and the original distribution does not have a normal distribution the methods of this section do not apply.

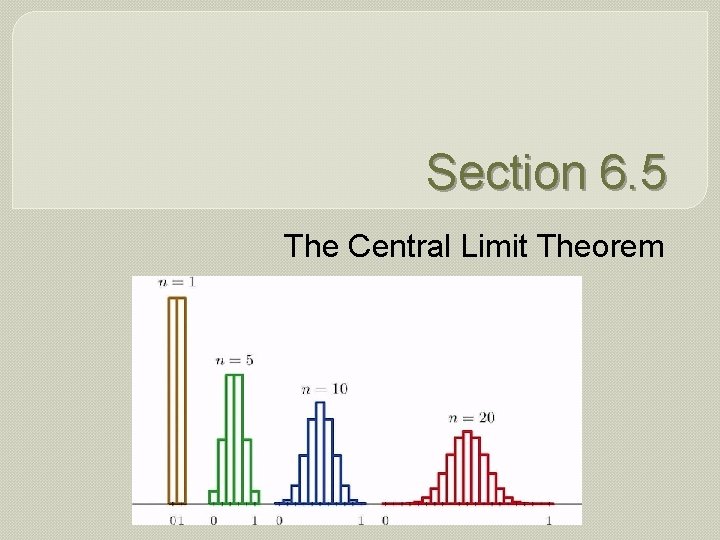
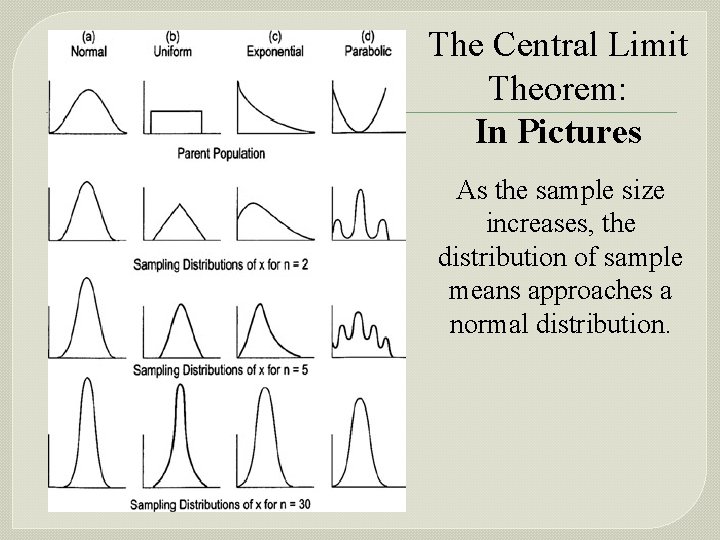
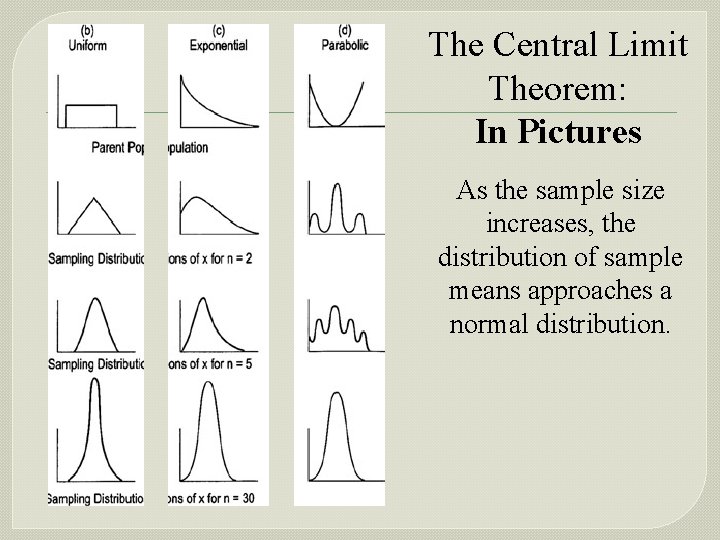
The Central Limit Theorem: In Pictures As the sample size increases, the distribution of

The Central Limit Theorem: In Pictures As the sample size increases, the distribution of sample means approaches a normal distribution.

The Central Limit Theorem: In Pictures As the sample size increases, the distribution of

The Central Limit Theorem: In Pictures As the sample size increases, the distribution of sample means approaches a normal distribution.

Important Points to Note • As the sample size increases, the distribution of sample

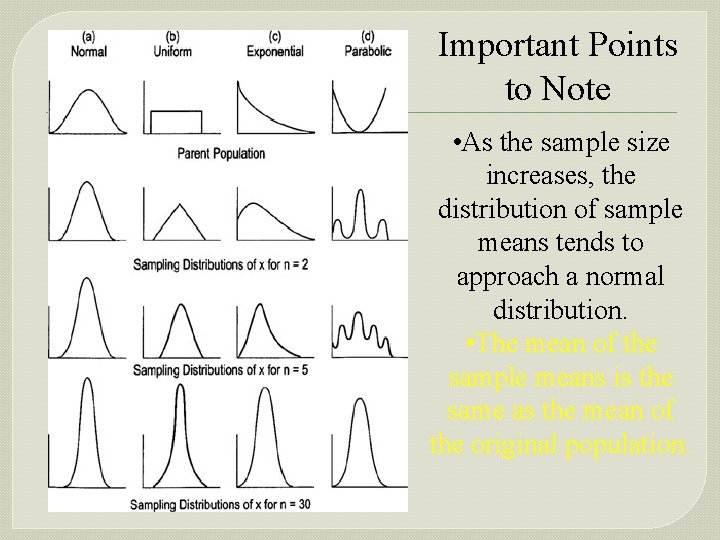
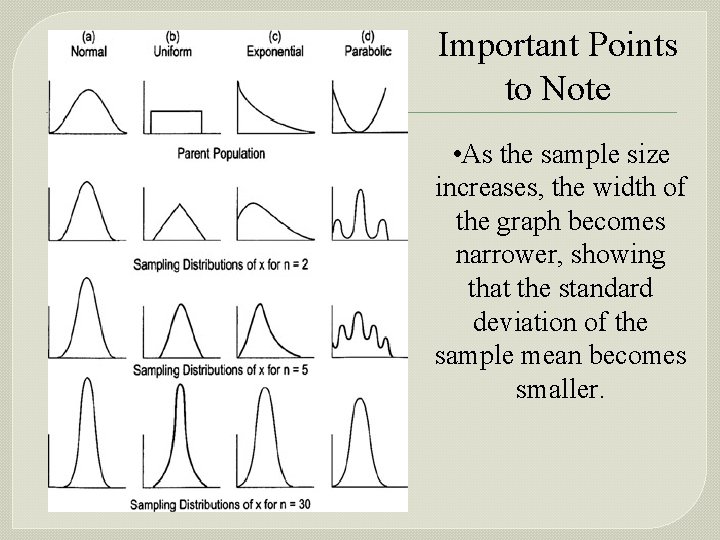
Important Points to Note • As the sample size increases, the distribution of sample means tends to approach a normal distribution. • The mean of the sample means is the same as the mean of the original population.

Important Points to Note • As the sample size increases, the width of the

Important Points to Note • As the sample size increases, the width of the graph becomes narrower, showing that the standard deviation of the sample mean becomes smaller.

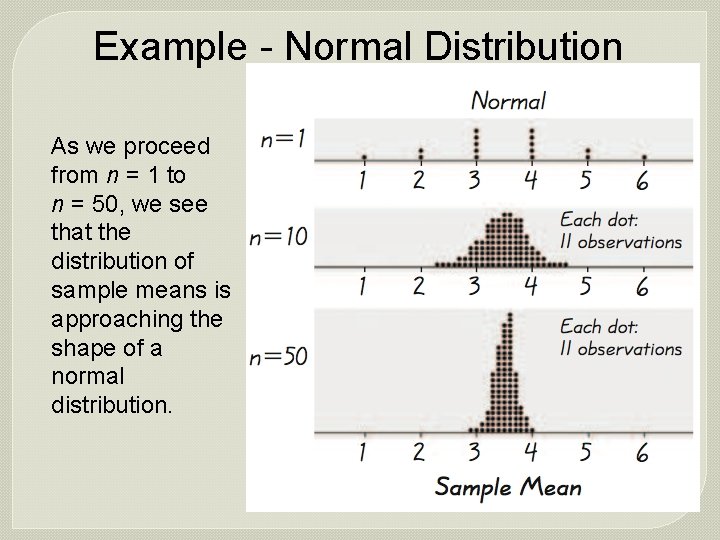
Example - Normal Distribution As we proceed from n = 1 to n =

Example - Normal Distribution As we proceed from n = 1 to n = 50, we see that the distribution of sample means is approaching the shape of a normal distribution.

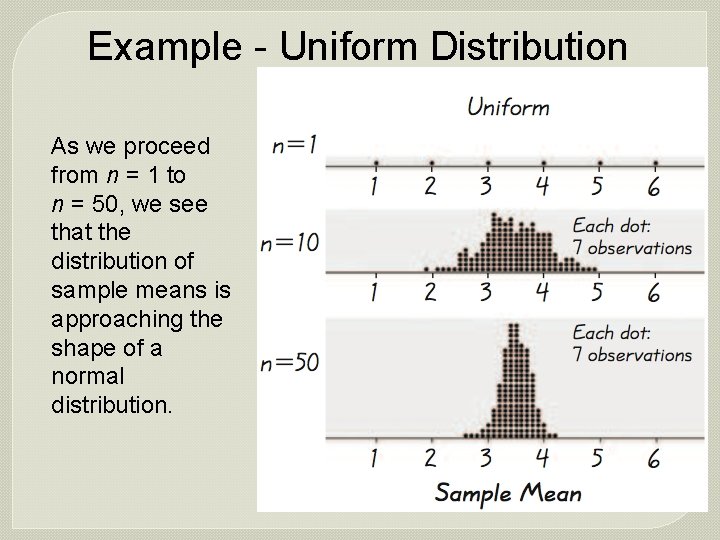
Example - Uniform Distribution As we proceed from n = 1 to n =

Example - Uniform Distribution As we proceed from n = 1 to n = 50, we see that the distribution of sample means is approaching the shape of a normal distribution.

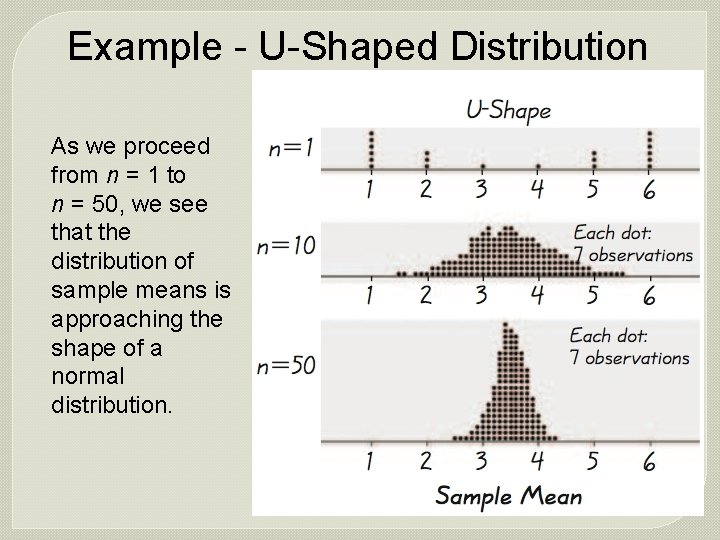
Example - U-Shaped Distribution As we proceed from n = 1 to n =

Example - U-Shaped Distribution As we proceed from n = 1 to n = 50, we see that the distribution of sample means is approaching the shape of a normal distribution.

Important Point As the sample size increases, the sampling distribution of sample means approaches

Important Point As the sample size increases, the sampling distribution of sample means approaches a normal distribution. **Take away from Section 6. 5 – when n > 30, the distribution is calculated as a normal distribution even if it was initially not normally distributed (ie. Uniform Distribution, U-Shape Distribution, or even a Skewed Distribution with Outliers).

Cool … So Why Do We Care? Think of what happens when we have

Cool … So Why Do We Care? Think of what happens when we have a normal distribution. What can we do? • Calculate any area, therefore any probability. The central limit theorem shows us that most samples can fit a normal distribution. So our calculation power (and therefore understanding) is endless!!!

Notation the mean of the sample means µx = µ the standard deviation of

Notation the mean of the sample means µx = µ the standard deviation of sample mean x = n (often called the standard error of the mean)

Notation the mean of the sample means µx = µ the standard deviation of

Notation the mean of the sample means µx = µ the standard deviation of sample mean x = n (often called the standard error of the mean)

The Fundamental Difference INDIVIDUAL VALUE When working with an individual value from a normally

The Fundamental Difference INDIVIDUAL VALUE When working with an individual value from a normally distributed population, use the methods of Section 6. 3. SAMPLE OF VALUES When working with a mean for some sample be sure to use the value of for the standard deviation of the sample mean.

Method for Finding Nonstandard Normal Distribution Areas or Probabilities a b a a

Method for Finding Nonstandard Normal Distribution Areas or Probabilities a b a a

Water Taxi Safety � Previously, we talked about the Baltimore water taxi that sank

Water Taxi Safety � Previously, we talked about the Baltimore water taxi that sank because of old weight limit standards. The water taxi assumed that the average person weight was 140 lbs. � Given that today the weights of men are normally distributed with a mean of 172 lbs and a standard deviation of 29 lbs. Find the probability that if an individual man is randomly selected, his weight will be greater than 175 lbs.

To find the probability of an individual man is randomly selected, we need to

To find the probability of an individual man is randomly selected, we need to use the command in the calculator: normalcdf(175, 9999, 172, 29) = 0. 4588. P(W > 175) = 0. 4588 175 s = 29 µ = 172,

Water Taxi Safety � Previously, we talked about the Baltimore water taxi that sank

Water Taxi Safety � Previously, we talked about the Baltimore water taxi that sank because of old weight limit standards. The water taxi assumed that the average person weight was 140 lbs. � Given that today the weights of men are normally distributed with a mean of 172 lbs and a standard deviation of 29 lbs. Find the probability that 20 randomly selected men will have a mean weight that is greater than 175 lbs (so that their total weight exceeds the current safe capacity of 3500 lbs).

µ = 172, 175 s = 29 It is much easier for an

µ = 172, 175 s = 29 It is much easier for an individual to deviate from the mean than it is for a group of 20 to deviate from the mean.

Example - cont a) Find the probability that if an individual man is randomly

Example - cont a) Find the probability that if an individual man is randomly selected, his weight is greater than 175 lb. P(x > 175) = 0. 4588 b) Find the probability that 20 randomly selected men will have a mean weight that is greater than 175 lb (so that their total weight exceeds the safe capacity of 3500 pounds). P(x > 175) = 0. 3218 It is much easier for an individual to deviate from the mean than it is for a group of 20 to deviate from the mean.

Interpretation of Results Given that the safe capacity of the water taxi is 3500

Interpretation of Results Given that the safe capacity of the water taxi is 3500 pounds, there is a fairly good chance (with probability 0. 3218) that it will be overloaded with 20 randomly selected men.

Example: When women were allowed to become pilots of fighter jets, engineers needed to

Example: When women were allowed to become pilots of fighter jets, engineers needed to redesign the ejection seats because they had originally been designed for men only. The ACES-II ejection seats were designed for men weighing between 140 lb and 211 lb. The weights of women have a mean of 143 lb and a standard deviation of 29 lb. (based on data from the National Health Survey. ) If 36 different women are randomly selected, find the probability that their mean weight is between 140 lb and 211 lb.

Reminder!!! The central limit theorem works if the sample size is greater than 30,

Reminder!!! The central limit theorem works if the sample size is greater than 30, or if the original population is normally distributed.

Recap In this section we have discussed: 1. Central limit theorem. 2. Practical rules.

Recap In this section we have discussed: 1. Central limit theorem. 2. Practical rules. 3. Effects of sample sizes. 4. Correction for a finite population.

Homework Pg. 295 -296 #2, 5 -7

Homework Pg. 295 -296 #2, 5 -7

Central limit theorem outlines Central limit theorem CLTCentral limit theorem outlines Central limit theorem CLT
Central Limit Theorem The central limit theorem andCentral Limit Theorem The central limit theorem and
Central limit theorem outlines Central limit theorem CLTCentral limit theorem outlines Central limit theorem CLT
Central Limit Theorem The theorem states that theCentral Limit Theorem The theorem states that the
LIMIT FUNGSI ALJABAR Limit fungsi aljabar LIMIT FUNGSILIMIT FUNGSI ALJABAR Limit fungsi aljabar LIMIT FUNGSI
Limit Sets Limit Sets Defined Limit Sets groupsLimit Sets Limit Sets Defined Limit Sets groups
LIMIT FUNGSI LIMIT FUNGSI PENGERTIAN LIMIT Perhatikan fungsiLIMIT FUNGSI LIMIT FUNGSI PENGERTIAN LIMIT Perhatikan fungsi
Limit MATHEMATICS LIMIT CRASH COURSE Limit of aLimit MATHEMATICS LIMIT CRASH COURSE Limit of a
limit Limit f limit f 0limit f xlimit Limit f limit f 0limit f x
Central Limit Theorem l Sampling Distributions l CentralCentral Limit Theorem l Sampling Distributions l Central
Ch 7 Central Limit Theorem Use the CentralCh 7 Central Limit Theorem Use the Central
Central Limit Theorem Section 5 5 M ACentral Limit Theorem Section 5 5 M A
Section 6 5 The Central Limit Theorem DistributionSection 6 5 The Central Limit Theorem Distribution
The Central Limit Theorem Section 9 3 2The Central Limit Theorem Section 9 3 2
Section 6 5 The Central Limit Theorem THESection 6 5 The Central Limit Theorem THE
SHAPE SPACE Pythagorean Theorem Pythagorean Theorem Pythagorean TheoremSHAPE SPACE Pythagorean Theorem Pythagorean Theorem Pythagorean Theorem
LEMIs Theorem Lamis Theorem Statement Lamis theorem isLEMIs Theorem Lamis Theorem Statement Lamis theorem is
VARIGNONS THEOREM What is Varigons Theorem The theoremVARIGNONS THEOREM What is Varigons Theorem The theorem
Thvenins Theorem Thevenins Theorem Thevenins theorem simplifies theThvenins Theorem Thevenins Theorem Thevenins theorem simplifies the
LEMIs Theorem Lamis Theorem Statement Lamis theorem isLEMIs Theorem Lamis Theorem Statement Lamis theorem is
Bayes Theorem Basics Total probability Theorem Bayes TheoremBayes Theorem Basics Total probability Theorem Bayes Theorem
BINOMIAL THEOREM BINOMIAL THEOREM INTRODUCTION BINOMIAL THEOREM BINOMIALBINOMIAL THEOREM BINOMIAL THEOREM INTRODUCTION BINOMIAL THEOREM BINOMIAL
CENTRAL LIMIT THEOREM p p p specifies aCENTRAL LIMIT THEOREM p p p specifies a
1162014 7 3 B The Central Limit Theorem1162014 7 3 B The Central Limit Theorem