Section 6 5 The Central Limit Theorem Distribution

Section 6. 5 The Central Limit Theorem

Distribution of Sample Means Population (with mean µ and standard deviation σ) Distribution of Sample Means Normal (for any sample size n) Not normal with n > 30 Normal (approximately) Not normal with n ≤ 30 Not normal Mean of the Sample Means Standard Deviation of the Sample Means

Central Limit Theorem Given: 1. The random variable x has a distribution (which may or may not be normal) with mean µ and standard deviation σ. 2. Simple random samples all of size n are selected from the population. (The samples are selected so that all possible samples of the same size n have the same chance of being selected. )

Central Limit Theorem – cont. Conclusions: 1. The distribution of sample x will, as the sample size increases, approach a normal distribution. 2. The mean of the sample means is the population mean µ. 3. The standard deviation of all sample means is

Practical Rules Commonly Used 1. For samples of size n larger than 30, the distribution of the sample means can be approximated reasonably well by a normal distribution. The approximation gets closer to a normal distribution as the sample size n becomes larger. 2. If the original population is normally distributed, then for any sample size n, the sample means will be normally distributed (not just the values of n larger than 30).

Notation the mean of the sample means µx = µ the standard deviation of sample mean x = n (often called the standard error of the mean)
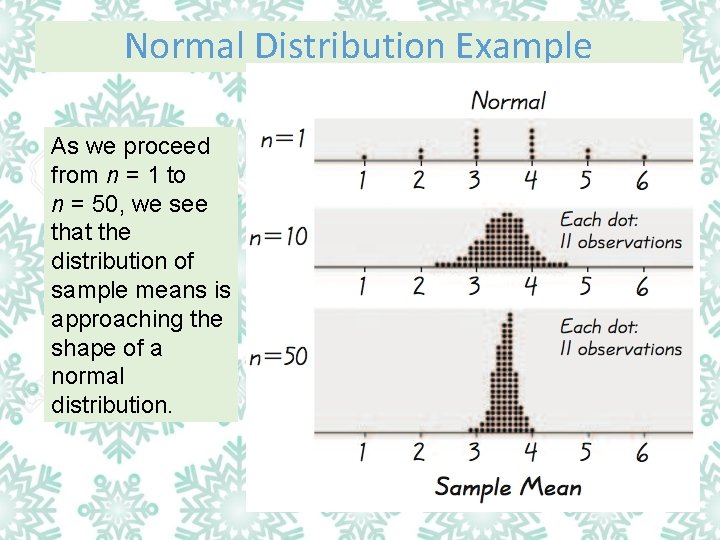
Normal Distribution Example As we proceed from n = 1 to n = 50, we see that the distribution of sample means is approaching the shape of a normal distribution.
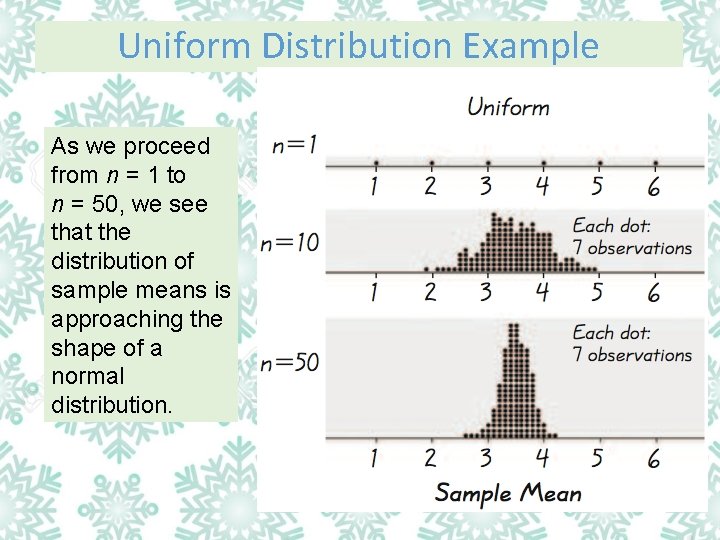
Uniform Distribution Example As we proceed from n = 1 to n = 50, we see that the distribution of sample means is approaching the shape of a normal distribution.
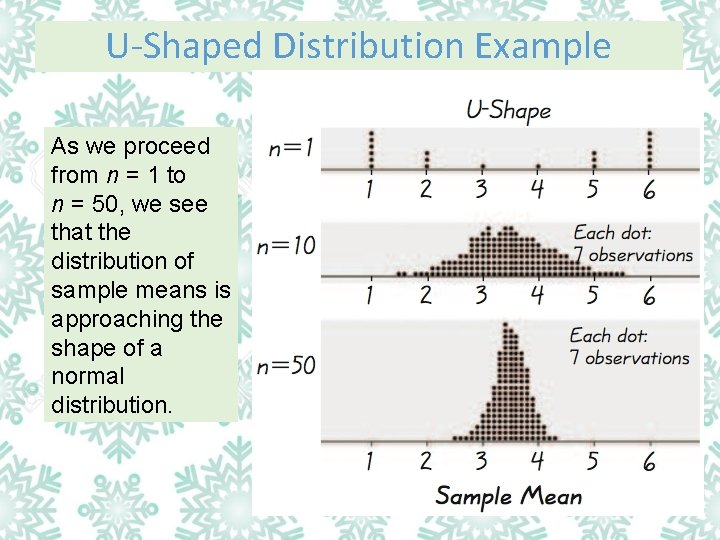
U-Shaped Distribution Example As we proceed from n = 1 to n = 50, we see that the distribution of sample means is approaching the shape of a normal distribution.

Important Point As the sample size increases, the sampling distribution of sample means approaches a normal distribution.
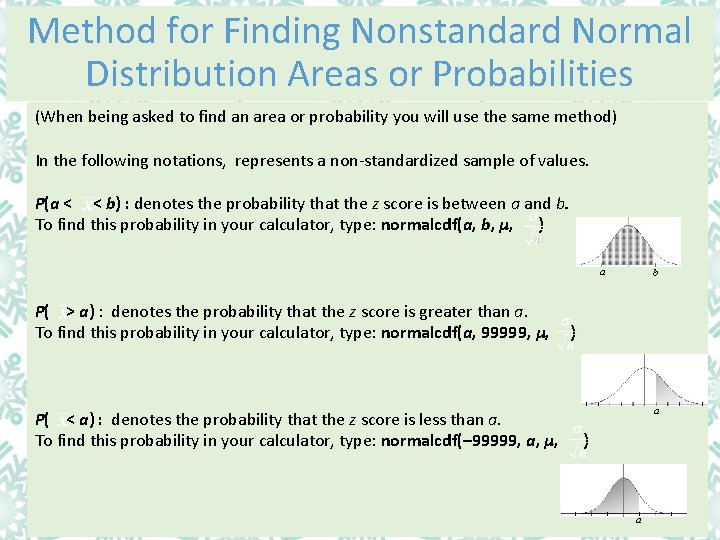
Method for Finding Nonstandard Normal Distribution Areas or Probabilities (When being asked to find an area or probability you will use the same method) In the following notations, represents a non-standardized sample of values. P(a < < b) : denotes the probability that the z score is between a and b. To find this probability in your calculator, type: normalcdf(a, b, µ, ) a P( > a) : denotes the probability that the z score is greater than a. To find this probability in your calculator, type: normalcdf(a, 99999, µ, P( < a) : denotes the probability that the z score is less than a. To find this probability in your calculator, type: normalcdf(– 99999, a, µ, b ) a

Example 1: Some passengers died when a water taxi sank in Baltimore’s Inner Harbor. Men are typically heavier than women and children, so when loading a water taxi, let’s assume a worst-case scenario in which all passengers are men. Based on data from the National Health and Nutrition Examination Survey, assume that the population of weights of men is normally distributed with µ = 172 lb and σ = 29 lb. a) Find the probability that if an individual man is randomly selected, his weight is greater than 175 lb.

Example 1: Use the Chapter Problem from page 249 of your textbook. It noted that some passengers died when a water taxi sank in Baltimore’s Inner Harbor. Men are typically heavier than women and children, so when loading a water taxi, let’s assume a worst-case scenario in which all passengers are men. Based on data from the National Health and Nutrition Examination Survey, assume that the population of weights of men is normally distributed with µ = 172 lb and σ = 29 lb. b) Find the probability that 20 randomly selected men will have a mean weight that is greater than 175 lb (so that their total weight exceeds the safe capacity of 3500 pounds).

Example 2: Cans of regular Coke are labeled to indicate that they contain 12 oz. Data Set 17 in Appendix B lists measured amounts for a sample of Coke cans. The corresponding sample statistics are n = 36 and = 12. 19 oz. If the Coke cans are filled so that µ = 12. 00 oz (as labeled) and the population standard deviation is σ = 0. 11 oz (based on the sample results), find the probability that a sample of 36 cans will have a mean of 12. 19 oz or greater.

Example 3: When women were allowed to become pilots of fighter jets, engineers needed to redesign the ejection seats because they had originally been designed for men only. The ACES-II ejection seats were designed for men weighing between 140 lb and 211 lb. The weights of women have a mean of 143 lb and a standard deviation of 29. (based on data from the National Health Survey. ) If 36 different women are randomly selected, find the probability that their mean weight is between 140 lb and 211 lb.
- Slides: 15