Central Limit Theorem l Sampling Distributions l Central

Central Limit Theorem l. Sampling Distributions l. Central Limit Theorem l. CLT for Sums l. CLT for Proportions

Sampling Distributions l Sampling Distribution: Given a population and sample size n, the sampling distribution of a statistic is the distribution of all values of the statistic for all possible samples of size n.

Sampling Distribution of the Mean l Sampling Distribution of the Mean: Given a population and sample size n, the sampling distribution of the mean is the distribution of all the means for all possible samples of size n.

Sampling Distributions Notation l The Mean of the Sample Means: l The Standard Deviation of the Sample Means

Sampling Distributions • • m = 3. 5 s ≈ 1. 12 mx = 3. 5 sx ≈ 0. 79

Simulations l http: //www. ltcconline. net/greenl/java/Stat istics/cltsimulation. html

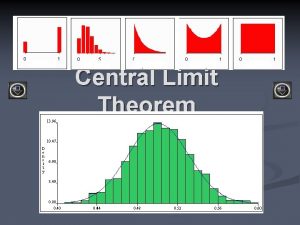
The Central Limit Theorem Let denote the mean of a random sample of size n from a population having mean m and standard deviation s. Then When the distribution of the population is normal so is the distribution of for any n. For large n, the distribution of is approximately normal regardless of the population distribution. Rule of Thumb: n > 30 is large

Sampling Distributions • • x: Unbiased Estimator • Range: 5 – 2 = 3 • Sample Ranges: 1, 2, 3, 1, 2, 1 • m. Range ≈ 1. 67 • Sample Range: Biased Estimator

Biased and Unbiased Estimator Unbiased estimator: A statistic whose sampling distribution has a mean that is equal to the population parameter. l The sample mean is an unbiased estimator for the population mean. l The sample proportion is an unbiased estimator for the population proportion. l The sample variance is an unbiased estimator for the population variance. l The sample range is a biased estimator for the population range.

CLT Example Suppose the average amount of time that it takes for college students to complete their degree is 4. 7 years. The standard deviation is 0. 3. What is the probability that 40 randomly selected college students will have an average completion time of less than 4. 4 years?
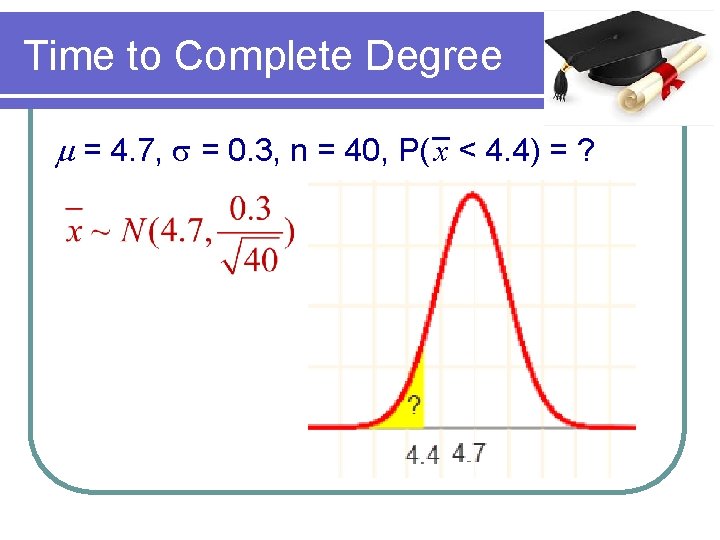
Time to Complete Degree m = 4. 7, s = 0. 3, n = 40, P( x < 4. 4) = ?
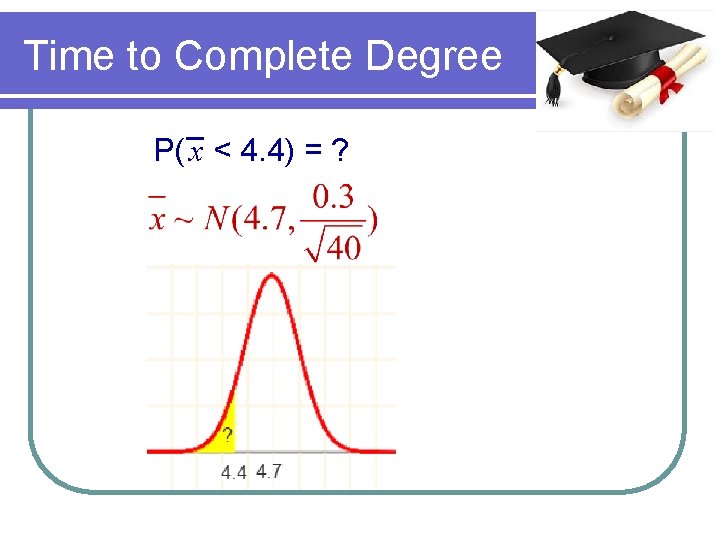
Time to Complete Degree P( x < 4. 4) = ?

CLT Example Suppose stock increases are normally distributed with a mean of 3 percent and a standard deviation of 5 percent. If your (randomly selected portfolio) consists of 20 stocks, what is the probability that your portfolio will lose money?
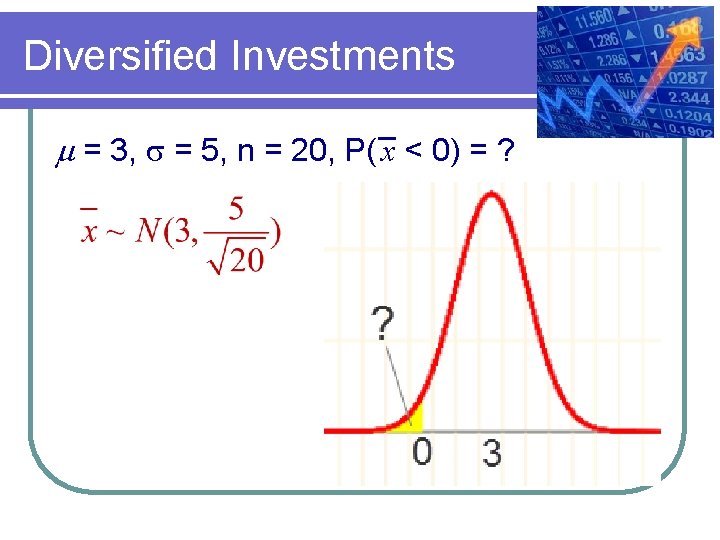
Diversified Investments m = 3, s = 5, n = 20, P( x < 0) = ?

Diversified Investments P( x < 0) = ?

CLT Example Suppose the average GPA of college students is 3. 1 and the standard deviation is 0. 7. A class of 35 randomly selected students will be considered high risk if their mean GPA is in the bottom 2 nd percentile. What is the largest mean GPA that will be considered high risk?
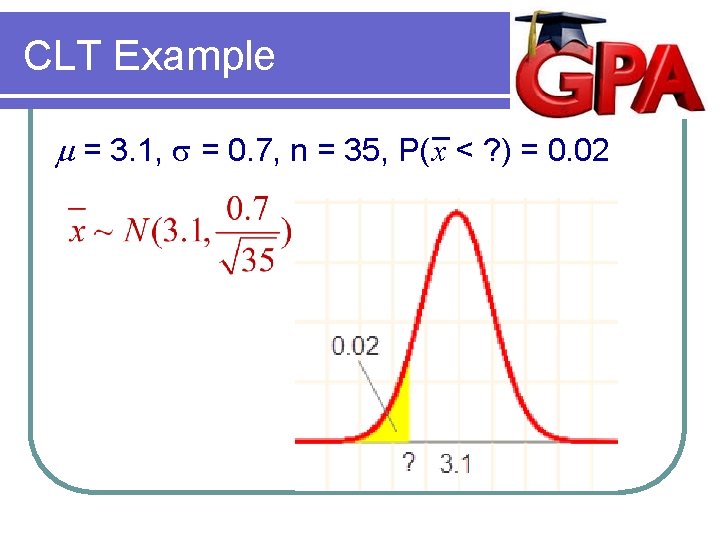
CLT Example m = 3. 1, s = 0. 7, n = 35, P( x < ? ) = 0. 02
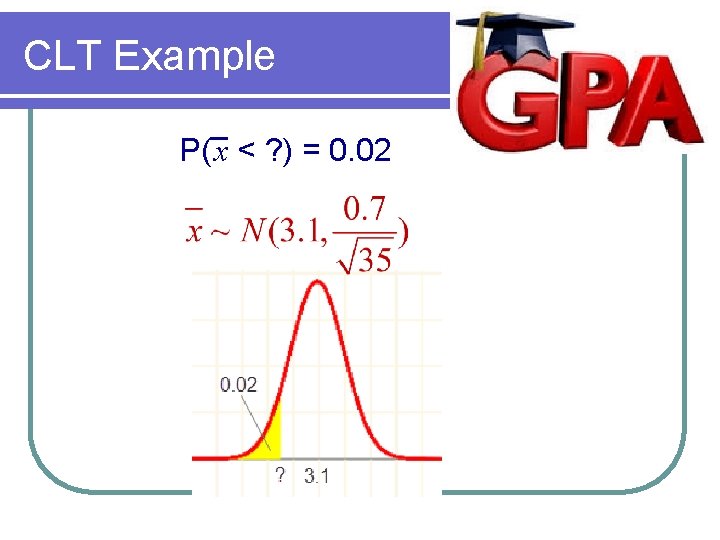
CLT Example P( x < ? ) = 0. 02

Central Limit Theorem for Sums If the collection of all random samples of size n are taken from a population having mean m and standard deviation s, then the sampling distribution of the sums will have mean nm and standard deviation. l If the population is normally distributed or if the sample size is large, then the distribution of the sums is also approximately normal. l

Central Limit for Sums Example The average family that goes to the carnival spends $65. The standard deviation is $15. If 80 randomly selected families are chosen, what is the probability that they will spend a total of more than $5, 000?
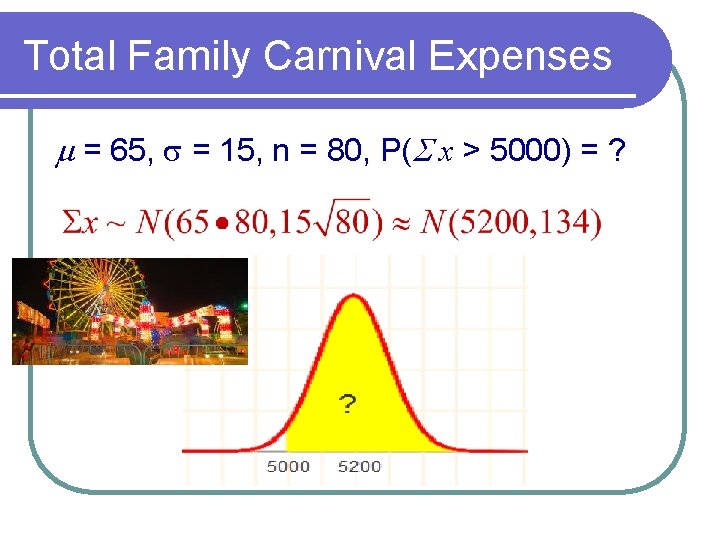
Total Family Carnival Expenses m = 65, s = 15, n = 80, P(S x > 5000) = ?
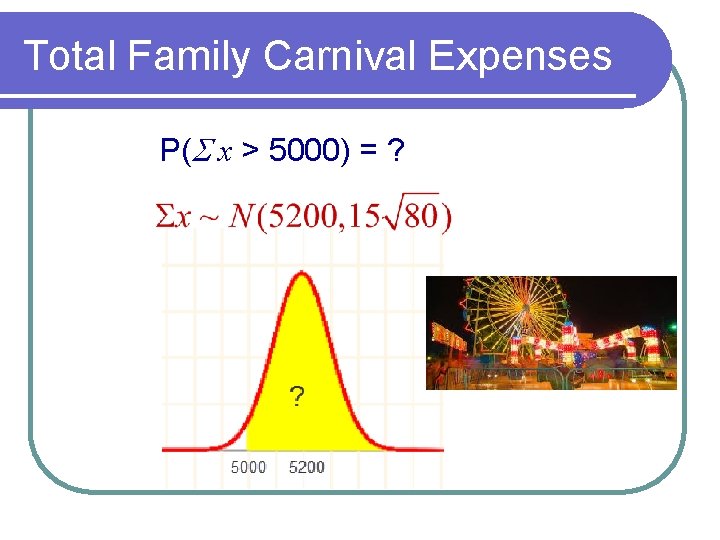
Total Family Carnival Expenses P(S x > 5000) = ?

The CLT for Proportions l Requirements: Must be a Binomial Distribution with np > 5, nq > 5 (q = 1 - p) l Conclusion: This Binomial Distribution is approximately normal with

Example Twelve percent of the US population is left handed. If 200 randomly selected Americans are surveyed, what is the probability that fewer than 20 of them are left handed?
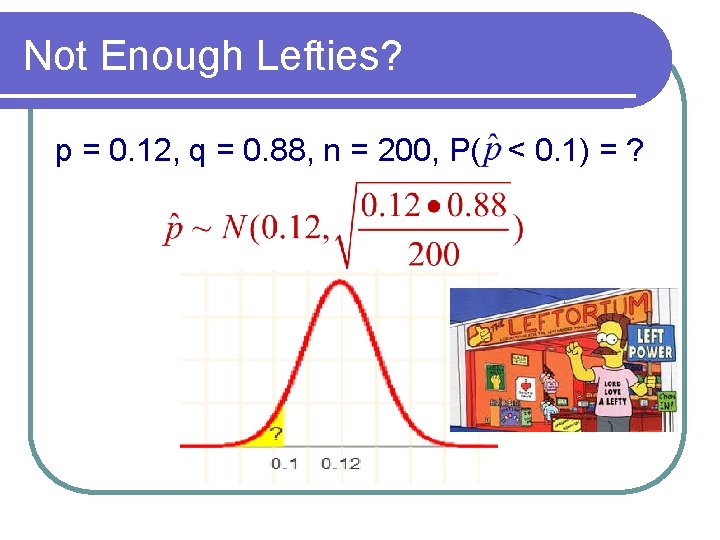
Not Enough Lefties? p = 0. 12, q = 0. 88, n = 200, P( < 0. 1) = ?

Not Enough Lefties? P( < 0. 1) = ?

Example According to a recent Gallup poll, 18% of Americans are underemployed. If 150 Americans are randomly selected, find the probability that between 24 and 30 of them are underemployed.

Underemployment p = 0. 18, q = 0. 82, n = 150, P(0. 15 < < 0. 2)

Underemployment P(0. 15 < < 0. 2)
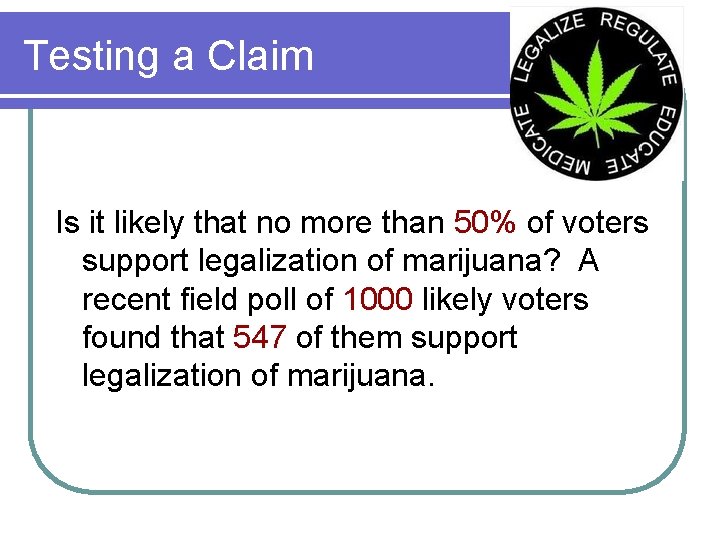
Testing a Claim Is it likely that no more than 50% of voters support legalization of marijuana? A recent field poll of 1000 likely voters found that 547 of them support legalization of marijuana.
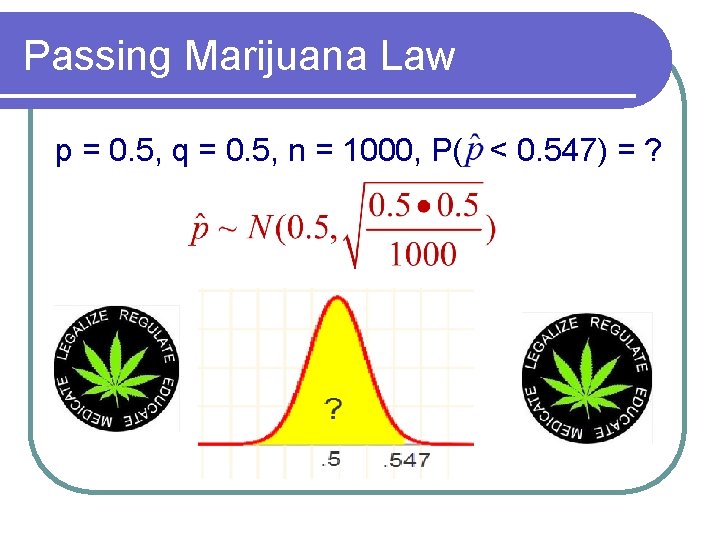
Passing Marijuana Law p = 0. 5, q = 0. 5, n = 1000, P( < 0. 547) = ?
- Slides: 31