Automated Theorem Proving Resolution and DavisPutnam Intermediate Logic

Automated Theorem Proving: Resolution and Davis-Putnam Intermediate Logic

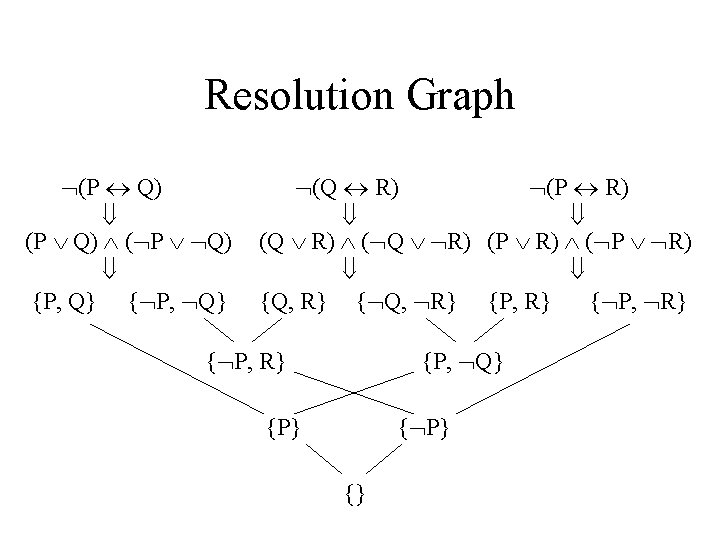
Resolution • Resolution is, like the tree method, a method to check for the logical consistency of a set of statements. • Resolution requires all sentences to be put into CNF. • A set of sentences in CNF is made into a clause set: a set of clauses, where a clause is a set of literals. • Clauses are resolved using the resolution rule, and the resulting clause (the resolvent) is added to the clause set: L C 1 L’ C 2 CNEW = C 1/L C 2/L’

Putting into CNF (P Q) (Equiv) ((P Q) (Q P)) (Impl) (( P Q) ( Q P)) (De. M) ( P Q) ( Q P) (P Q) (Q P) (De. M, DN) (Dist) ((P Q) P) (Dist) (P Q) ( Q Q) (P P) ( Q P)

Resolution Graph (P Q) ( P Q) {P, Q} { P, Q} (Q R) (P R) (Q R) ( Q R) (P R) ( P R) {Q, R} { Q, R} {P, R} { P, R} {P, Q} { P, R} {P} {}

Satisfiability • A clause is satisfied by a truth-value assignment if and only if that assignment makes at least one literal in that clause true. • A clause set is satisfiable if and only if there is a truthvalue assignment that satisfies all clauses in that clause set. • Figuring out whether some clause set is satisfiable is the satisfiability problem. • Note how the satisfiability problem relates directly to the consistency problem: figuring out whether some set of statements is consistent. • A set of sentences is consistent if and only if the corresponding clause set is satisfiable.

Soundness and Completeness of Resolution • The rule of Resolution is sound, making the method of resolution sound as well (so, if the empty clause (which is a generalized disjunction of 0 disjuncts, which is a contradiction) can be resolved from a clause set, then that means that clause set is indeed unsatisfiable. • It can be shown that resolution is complete, i. e. that the empty clause can be resolved from any unsatisfiable clause set.

Resolutions as Derivations A (B C) (A B) (A C) (A B) (D E) ( A D E) ( B D E) E A (C D) C D (A B) (D E) ( A B) (D E) 17. 42 from LPL: A (B C) E (A B) (D E) A C D 1. {A, B} 2. {A, C} 3. { A, D, E} 4. { B, D, E} 5. { E} 6. { A} 7. { C, D} 1, 6 8. {B} 2, 6 9. {C} 4, 8 10. {D, E} 5, 10 11. {D} 7, 9 12. { D} 11, 12 13. {}

Resolutions as Decision Procedures • Resolution can be made into a decision procedure by systematically exhausting all possible resolvents (of which there are finitely many). • This will not be very efficient unless we add some resolution strategies.

Resolution Strategies • Clause Elimination Strategies – Tautology Elimination – Subsumption Elimination – Pure Literal Elimination • Resolving Strategies – – Unit Preference Resolution Linear Resolution Ordered Resolution Etc.

Tautology Elimination • A tautologous clause is a clause that contains an atomic statement as well as the negation of that atomic statement. • Obviously, for any tautologous clause C, any truth -value assignment is going to satisfy C. • Hence, with S any clause set, and with S’ the clause set S with all tautologous clauses removed: S is satisfiable if and only if S’ is satisfiable.

Subsumption Elimination • A clause C 1 subsumes a clause C 2 if and only if every literal contained in C 1 is contained in C 1, i. e. C 1 C 2. • Obviously, if C 1 subsumes C 2 , then any truthvalue assignment that satisfies C 1 will satisfy C 2. • Hence, with S any clause set, and S’ the clause set S with all subsumed clauses removed: S is satisfiable if and only if S’ is satisfiable.

Pure Literal Elimination • A literal L is pure with regard to a clause set S if and only if L is contained in at least one clause in S, but L’ is not. • A clause is pure with regard to a clause set S if and only if it contains a pure literal. • Obviously, with S any clause set, and with S’ the clause set S with all pure clauses removed: S is satisfiable if and only if S’ is satisfiable.

Unit Preference Resolution • A unit clause is a clause that contains one literal. • Unit preference resolution tries to resolve using unit clauses first.

Unit Literal Deletion and Splitting • For any clause set S, SL is the clause set that is generated from S as follows: – Remove all clauses from S that contain L. – Remove all instances of L’ from all other clauses • Obviously, with C = {L} S, S is satisfiable if and only if SL is satisfiable. • It is also easy to see that for any clause set S, and any literal L: S is satisfiable if and only if SL is satisfiable or SL’ is satisfiable. • The last observation suggests a splitting strategy that forms the basis of Davis-Putnam.

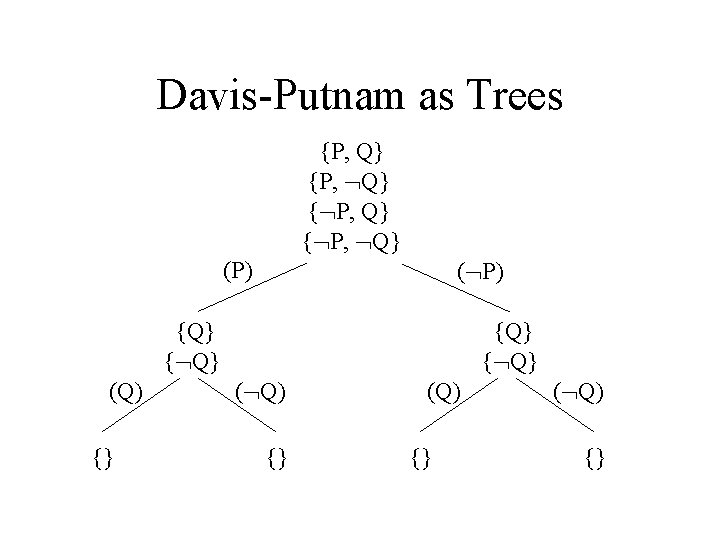
Davis-Putnam • Recursive routine Satisfiable(S) returns true iff S is satisfiable: boolean Satisfiable(S) begin if S = {} return true; if S = {{}} return false; select L lit(S); return Satisfiable(SL) || Satisfiable(SL’); end

Making Davis-Putnam Efficient: Adding Bells and Whistles • The routine on the previous slide is not very efficient. However, we can easily make it more efficient: – – return false as soon as {} S add the unit rule: if {L} S return Satisfiable(SL) strategically add deletion strategies strategically choose the literal on which to split • As far as I have gathered from the ATP literature, such efficient Davis-Putnam routines are credited to do well in comparison to other ATP routines.

Davis-Putnam as Trees {P, Q} {P, Q} { P, Q} (P) ( P) {Q} { Q} (Q) {} {Q} { Q} ( Q) {}

Davis-Putnam vs Truth-Trees • How does Davis-Putnam differ from Truth-Trees? – Davis-Putnam can be seen as an ‘inside-out’ approach: it assigns a truth-value to atomic statements and determines the consequences of that assignment for the complex statements involved. – Truth-Trees are more of an ‘outside-in’ approach: it assigns truth-values to complex statements as a whole, and decomposes them accordingly until they have been decomposed to literals. • How does the Davis-Putnam procedure stack up against the Truth-Tree procedure in terms of efficiency? – No idea … project!

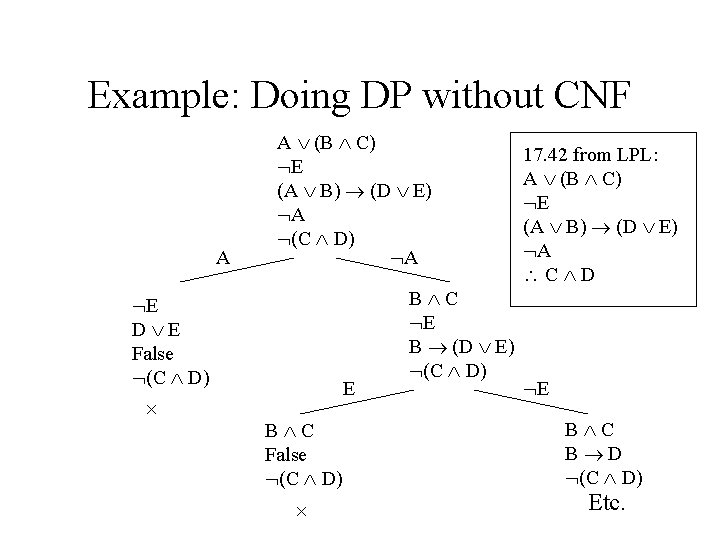
Can we do DP without CNF? • Sure, simply consider a set of statements, and see what happens to each of the statements when some atomic claim is set to true or false, respectively. • For example, when we set A to True in (A B) (D E), the claim becomes (True B) (D E), which becomes True (D E), which becomes D E. • Possible project: Investigate efficiency of this method

Rules for DP without CNF True False True P P True P P False True False P P False P True False P P P True P True P P False P P False P

Example: Doing DP without CNF A A (B C) E (A B) (D E) A (C D) A E D E False (C D) × E B C False (C D) × B C E B (D E) (C D) 17. 42 from LPL: A (B C) E (A B) (D E) A C D E B C B D (C D) Etc.

Can DP and TT be combined? • DP really starts to look like a tree method, even though DP works ‘inside-out’ and TT ‘outside-in’. • Can these two methods be combined into one method? • Sure! In fact, you can do some things to make this efficient, e. g: – Use ‘inheritance’ to keep from copying statements that are unaffected. • Project: Investigate efficiency of this method • Project: Do the KE rules add any further efficiency?

Example: DP and TT Combo A B C (D E) D C A E (C B) C B D E D A A E E × 17. 42 from LPL: A B C (D E) D C A E C B (you’ll probably have to reconstruct this one to follow it; it would help if it were annotated with justifications!)

EG and ATP • EGTT: Applying Truth-Trees to EG • EGDP: Applying Davis-Putnam to EG • EGTTDP: Applying both TT and DP to EG

EGTT: Applying Truth-Trees to EG • Applying the idea of truth-trees to EG is simple: – Two decomposition rules: 1 2 1 2 – Close any branch that contains a literal and its complement, or that contains an empty cut. – Rest remains the same

EGTT: A Satisfiability Procedure boolean Satisfiable(G) begin return false; if G = L L return false; if G = 1 2 Satisfiable( else return true; end return Satisfiable( ); return 1 ) || Satisfiable( 2 );

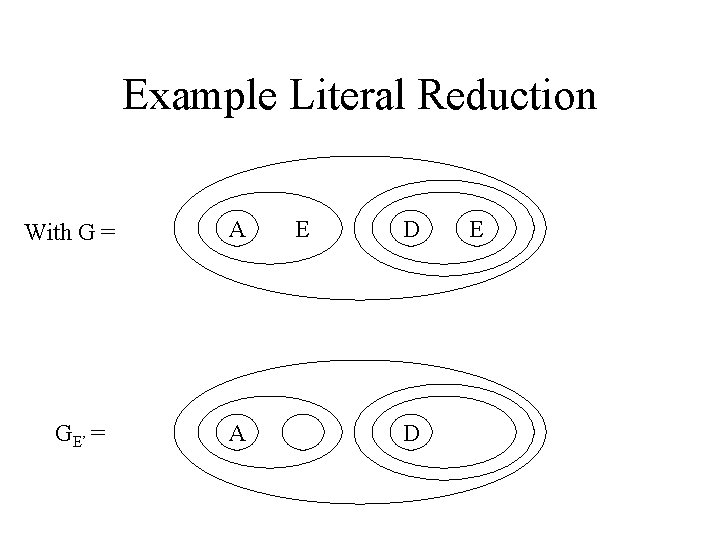
EGDP: Literal Reduction • For any graph , L is the graph that is generated from as follows: – Remove all instances of L – Replace all instances of L’ with an empty cut

Example Literal Reduction With G = GE’ = A A E D D E

EGDP: Satisfiability Decision Procedure boolean Satisfiable(G) begin if G = return true; if G = return false; select L lit(G); return Satisfiable(GL) || Satisfiable(GL’); end

Adding Bells and Whistles • Again, this procedure can be made a lot more efficient by dealing with empty cuts, double cuts, and duplicates more efficiently, by various other tautology, subsumption, and pure literal deletion strategies, and by strategically picking the literal on which to split.

Tautology Elimination in EG • Any subgraph of the following form (i. e. a cut containing an empty cut) is a tautology, and can therefore be eliminated: • Note: This can be incorporated into the reduction routine. That is, rather than replacing any complement of a literal with an empty cut, we can remove any cut containing the complement.

Subsumption Elimination in EG If a graph of the form: exists at a nested level with regard to: then the first graph is said to be subsumed by the second (subsuming) graph, and can therefore be removed.

Pure-Literal Elimination in EG • A literal that exists at even levels only is said to be a pure literal, and can be eliminated for satisfiability purposes. • A literal that exists at odd levels only is also a pure literal, and can be replaced with the empty cut for satisfiability purposes.

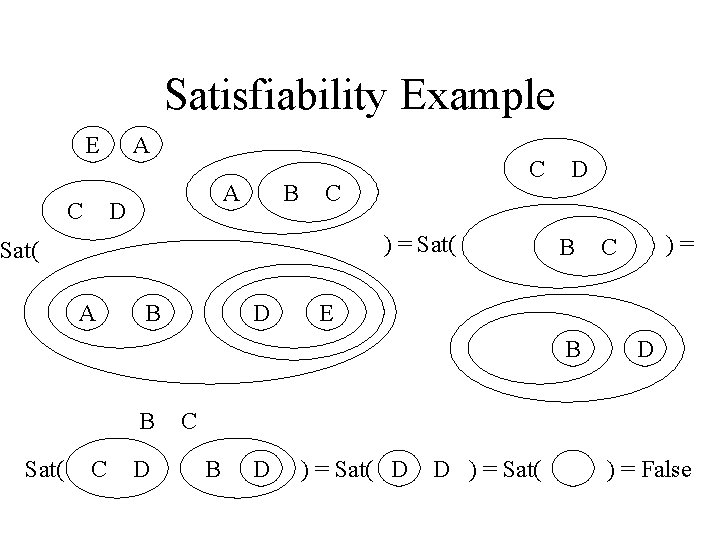
Satisfiability Example E C A A D B C C ) = Sat( A B D D B E B B Sat( C D )= C D C B D ) = Sat( D D ) = Sat( ) = False

Advantage of EGDP over DP? • The alleged advantage of EGDP over DP is that there is no need to put statements into clauses. This not only improves efficiency in that this preliminary step can eliminated, but by avoiding clauses, the algorithm actually becomes inherently more efficient in that 1) it leaves statements compact, and 2) it eliminates literals at any level. • Project: Investigate to see whether this is true!

Example: Gaining Efficiency by Avoiding Clauses A B B Clausifying DE (2 x!) A A B B C C C No Clausifying! A DC (2 x!) C A DE B C DC So, by keeping statements compact, less steps need to be taken!

EGTTDP • Can EG be combined with both TT and DP? • Yes, the characteristic rule of TT is the decomposition rule, and the characteristic rule for DP is the splitting rule. We can use both rules in a satisfiability procedure. • Question: When is a good time to use decomposition, and when is a good time to use splitting? … Project!

EGTTDP: A Satisfiability Procedure boolean Sat(G) begin remove double cuts; if G = return true; if G = (TT) if G = L return false; return Sat( L ); 1 2 return Sat( 1 ) || Sat( 2 ); (DP) select L lit(G); return Sat(GL) || Sat(GL’); end

HW 9 • Show the argument below to be valid using: – – – 1. Resolution 2. Davis-Putnam (on clauses) 3. Davis-Putnam (on original statements) 4. Davis-Putnam and Truth-Tree combo 5. EGTT, EGDP, and EGTTDP Q S (P Q) R S R --- P (Q S)