Automated Theorem Proving Lecture 4 Formula A A







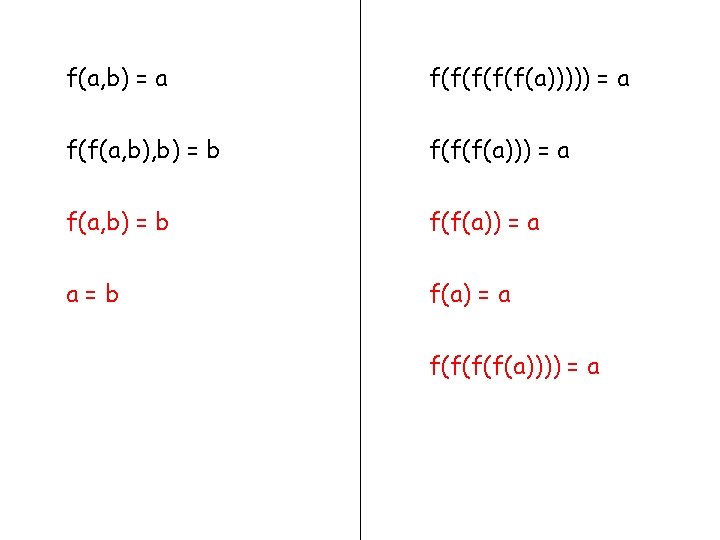












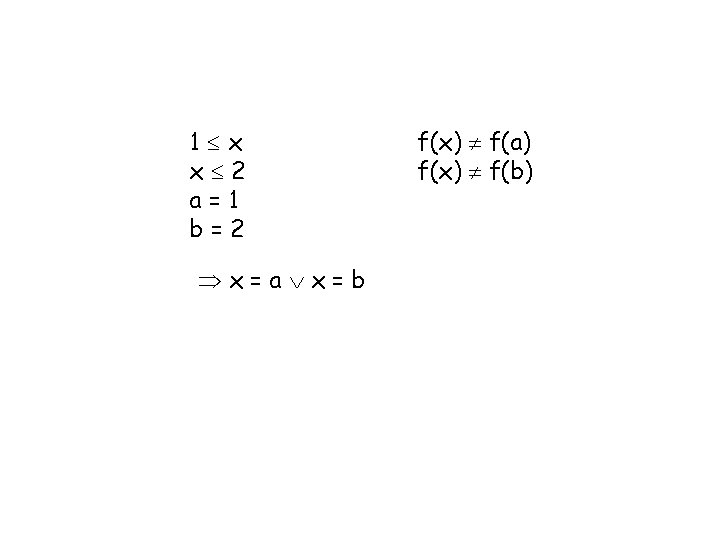

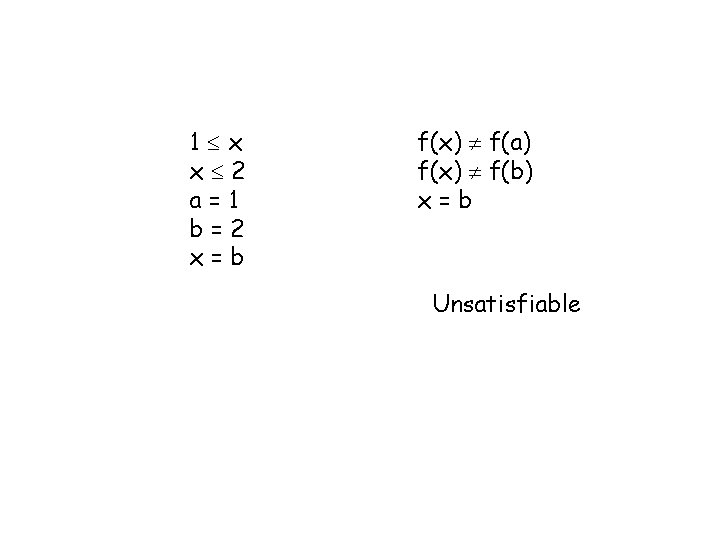

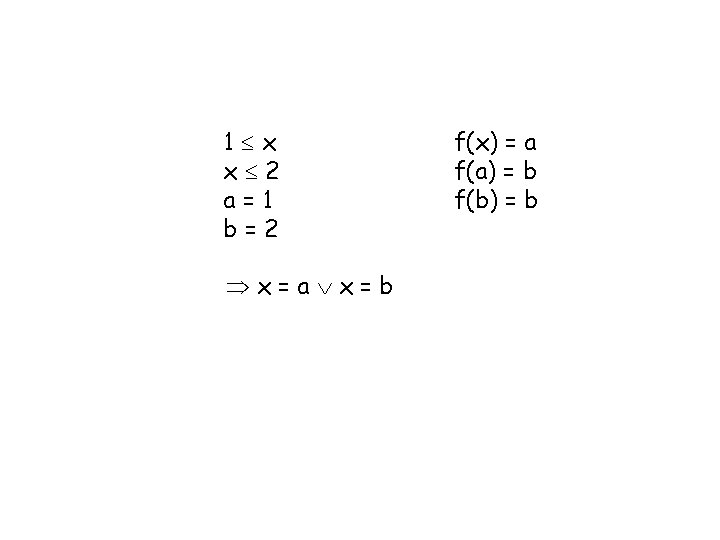



- Slides: 34

Automated Theorem Proving Lecture 4

Formula : = A | | A Atom : = b | t = 0 | t < 0 | t 0 t Term : = c | x | t + t | t – t | ct | Select(m, t) m Mem. Term : = f | Update(m, t, t) f Field b Sym. Bool. Const x Sym. Int. Const c {…, -1, 0, 1, …}

Memory axiom for all objects o and o’, and memories m: o = o’ Select(Update(m, o, v), o’) = v o o’ Select(Update(m, o, v), o’) = Select(m, o’)

{ b. f = 5 } a. f = 5 { a. f + b. f = 10 } iff Select(f, b) = 5 Select(Update(f, a, 5), a) + Select(Update(f, a, 5), b) 10 is unsatisfiable theory of arithmetic: 5, 10, + theory of arrays: Select, Update, f Constraints that arise in program verification are mixed!

Theories communicating via equality and variables Select(f, b) = 5 Select(Update(f, a, 5), a) + Select(Update(f, a, 5), b) 10 Introduce: variable w to represent Select(f, b) variable x to represent Select(Update(f, a, w), a) variable y to represent Select(Updatef, a, w), b) variables z and z’ to eliminate the arithmetic disequality Theory of arithmetic Theory of arrays x = w, y = w w=5 x+y=z z’ = 10 z = z’ w = Select(f, b) x = Select(Update(f, a, w), a) y = Select(Update(f, a, w), b) z z’

Theory of arrays Formula : = A | A Atom : = t | t t t Term : = c | Select(m, t) m Mem. Term : = f | Update(m, t, t) c Sym. Const for all objects o and o’, and memories m: o = o’ Select(Update(m, o, v), o’) = v o o’ Select(Update(m, o, v), o’) = Select(m, o’)

Theory of Equality with Uninterpreted Functions Formula : = A | A Atom : = t | t t t Term : = c | f(t, …, t) c Sym. Const f Function for all constants a and b and functions f: -a=a -a=b b=c a=c - a = b f(a) = f(b)
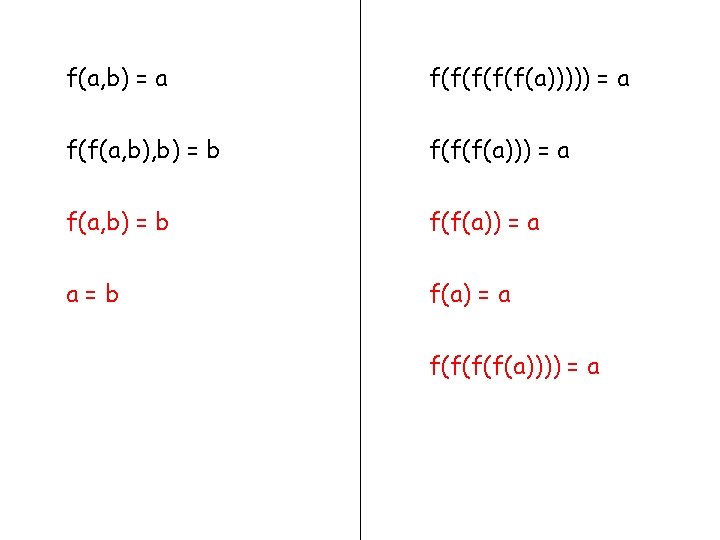
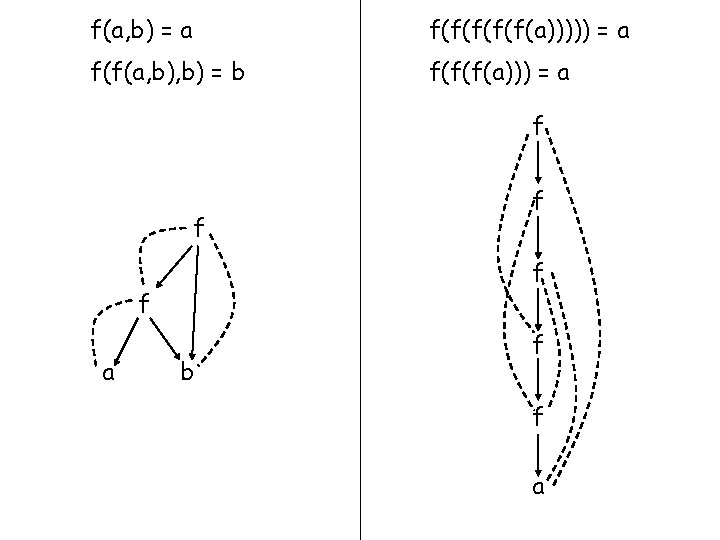
f(a, b) = a f(f(f(a))))) = a f(f(a, b) = b f(f(f(a))) = a f(a, b) = b f(f(a)) = a a=b f(a) = a f(f(a)))) = a

f(a, b) = a f(f(f(a))))) = a f(f(a, b) = b f(f(f(a))) = a f f a f b f f a

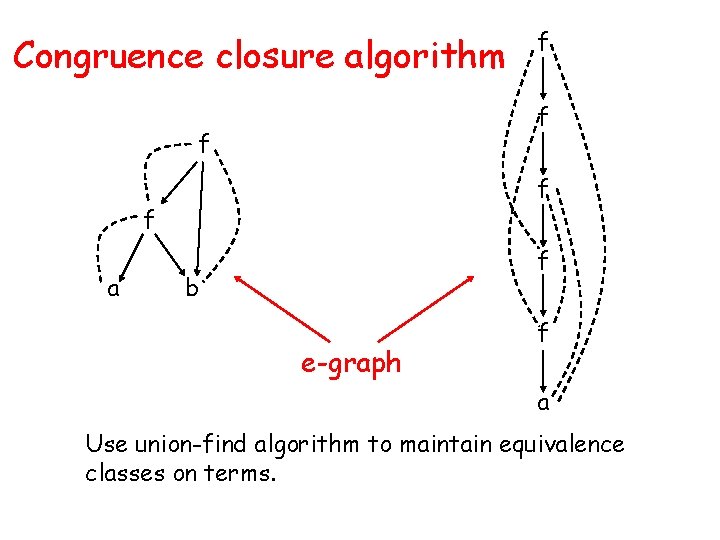
Congruence closure algorithm f f a f f b e-graph f a Use union-find algorithm to maintain equivalence classes on terms.

Decision procedure for EUF 1. Construct initial e-graph for all terms appearing in equalities and disequalities. 2. Apply congruence closure ignoring disequalities. 3. If there is a disequality t 1 t 2 and an equivalence class containing both t 1 and t 2, return unsatisfiable. 4. Otherwise, return satisfiable.

Soundness Theorem: If the algorithm returns unsatisfiable, the constraints are unsatisfiable. Lemma: At every step of the congruence closure algorithm, each equality in the e-graph is implied by the original set of equalities. Proof: By induction on the number of steps.

Completeness Theorem: If the algorithm returns satisfiable, there is a model satisfying the constraints.

Model A (finite or infinite) universe U An interpretation I - maps each constant symbol u to an element I(u) U - maps each function symbol f to a function I(f) (U U)

Completeness Theorem: If the algorithm returns satisfiable, there is a model satisfying the constraints. How do we construct the model?

f f(a, b) = a f(f(a, b) = b f a b For any term t in the e-graph, let EC(t) be the equivalence class containing t. U = set of equivalence classes + new element I(c) = EC(c) I(f)( ) = EC(f(u)), if u . f(u) is a term in the e-graph I(f)( ) = , otherwise

Convexity A conjunction of facts is convex if whenever it entails a disjunction of equalities, it also entails at least one equality by itself. If C a 1 = b 1 … an = bn Then there is i [1, n] such that C ai = bi A theory is convex if ever conjunction of facts in theory is convex.

EUF is convex Suppose C u 1 = t 1 u 2 = t 2 Then C u 1 t 1 u 2 t 2 is unsatisfiable The congruence closure algorithm demonstrates that there is some i such that even C ui ti is unsatisfiable

Uninterpreted theory Function symbols: f 1, f 2, … (each with an arity {0, 1, …}) Relation symbols: R 1, R 2, … (each with an arity {0, 1, …}) Special relation: equality (arity 2) Variables: x 1, x 2, … Boolean facts: x 1 = x 2, x 1 x 2, R(x 1, x 2), x. R(x, y) A conjunction of facts is consistent iff there is a model (U, I) that satisfies each fact in the conjunction. e. g. , EUF, arrays, lists

Interpreted theory Function symbols: f 1, f 2, … (each with an arity {0, 1, …}) Relation symbols: R 1, R 2, … (each with an arity {0, 1, …}) Special relation: equality (arity 2) Variables: x 1, x 2, … Boolean facts: x 1 = x 2, x 1 x 2, R(x 1, x 2), x. R(x, y) Fixed model (U, I) providing an interpretation for the function and relation symbols. A conjunction of facts is consistent iff I can be extended to the free variables of the conjunction so that each fact in the conjunction is satisfied. e. g. , arithmetic over rationals, arithmetic over integers

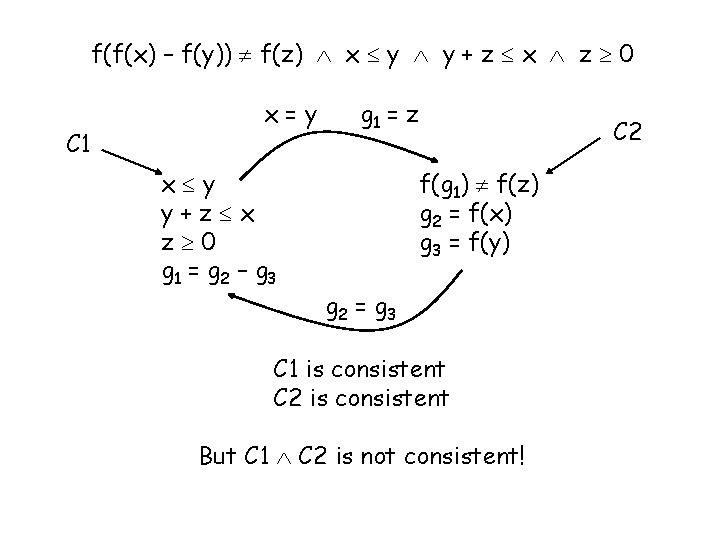
Communicating theories • Suppose the only shared symbols between two theories T 1 and T 2 are equality and variables • C 1 is conjunction of facts in theory T 1 • C 2 is conjunction of facts in theory T 2 • Suppose C 1 is consistent by itself and C 2 is consistent by itself • Is C 1 C 2 consistent?

f(f(x) – f(y)) f(z) x y y + z x z 0 C 1 x=y x y y+z x z 0 g 1 = g 2 – g 3 g 1 = z f(g 1) f(z) g 2 = f(x) g 3 = f(y) g 2 = g 3 C 1 is consistent C 2 is consistent But C 1 C 2 is not consistent! C 2

For any conjunction C 1 of facts in theory of rationals and any conjunction C 2 of facts in theory of EUF, it suffices to communicate equalities over shared variables. What if C 1 is a conjunction of facts in theory of arithmetic over integers?

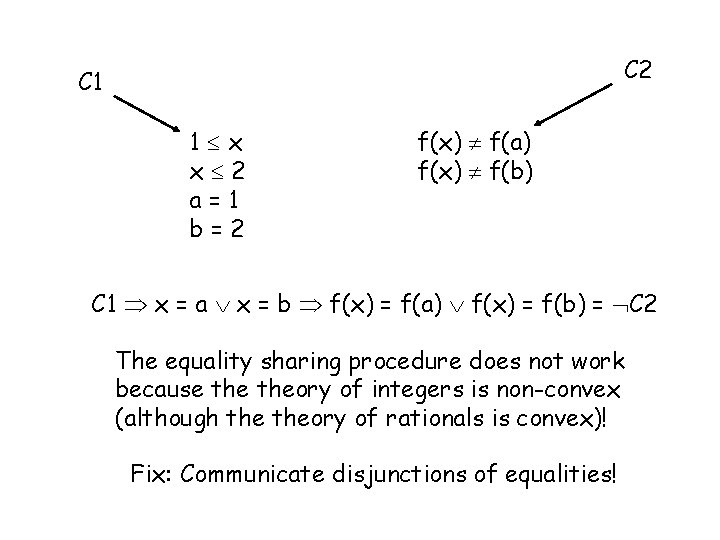
C 2 C 1 1 x x 2 a=1 b=2 f(x) f(a) f(x) f(b) C 1 x = a x = b f(x) = f(a) f(x) = f(b) = C 2 The equality sharing procedure does not work because theory of integers is non-convex (although theory of rationals is convex)! Fix: Communicate disjunctions of equalities!
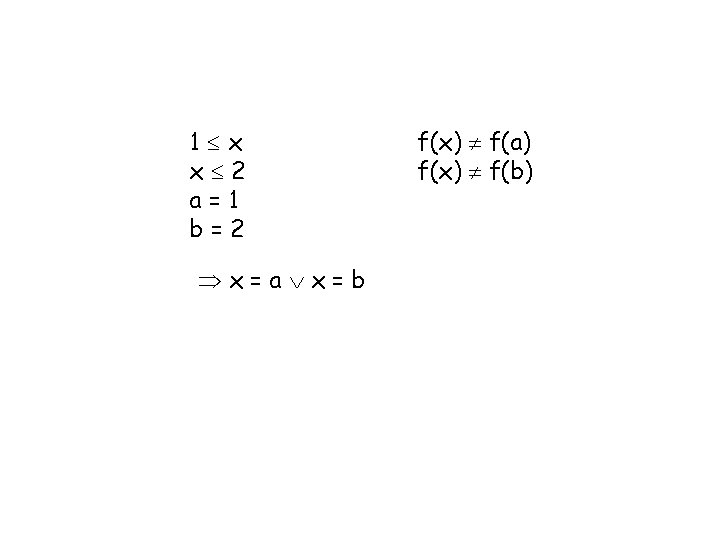
1 x x 2 a=1 b=2 x=a x=b f(x) f(a) f(x) f(b)

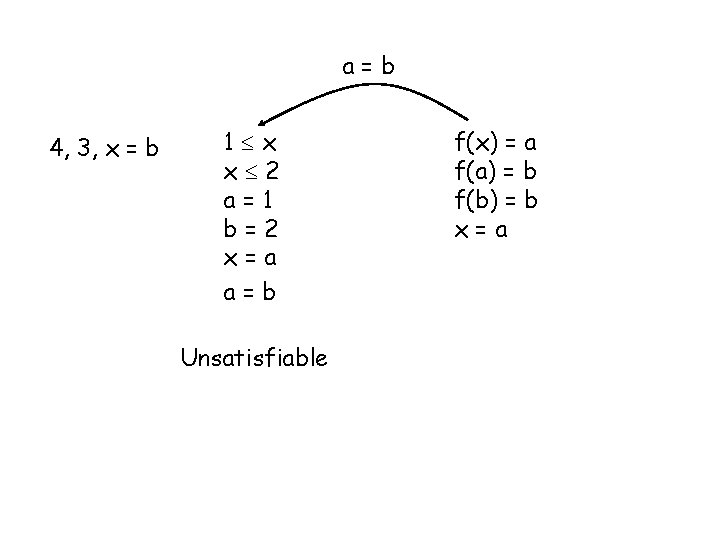
4, 2, x = b 1 x x 2 a=1 b=2 x=a f(x) f(a) f(x) f(b) x=a Unsatisfiable
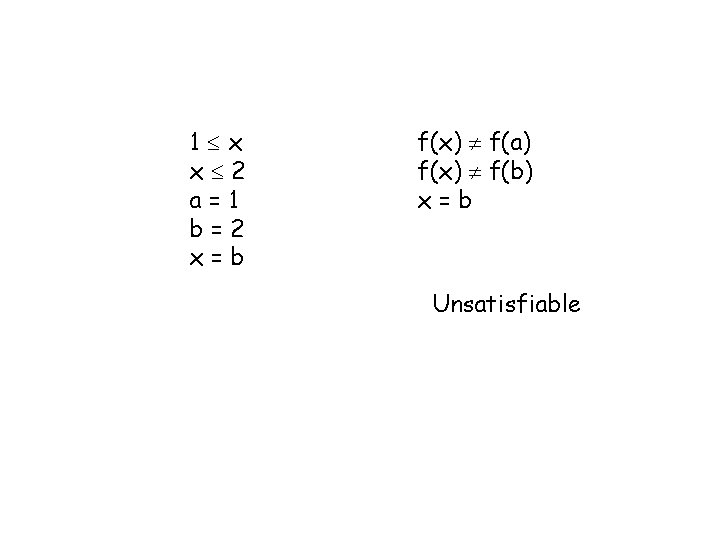
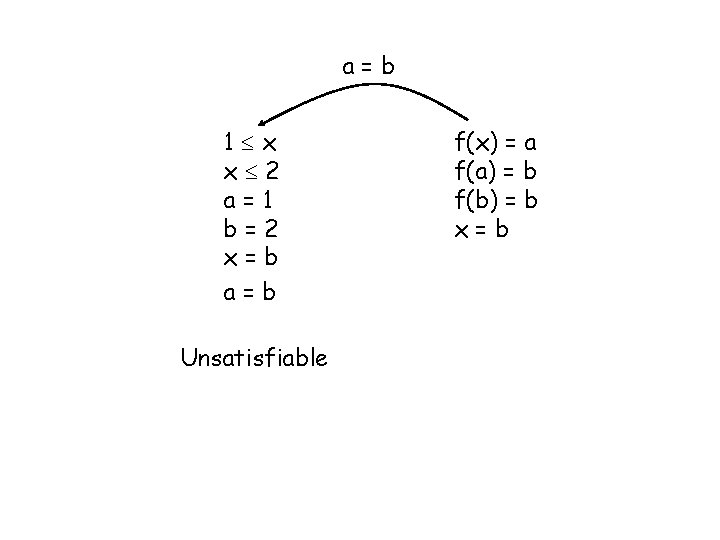
1 x x 2 a=1 b=2 x=b f(x) f(a) f(x) f(b) x=b Unsatisfiable

Another Example
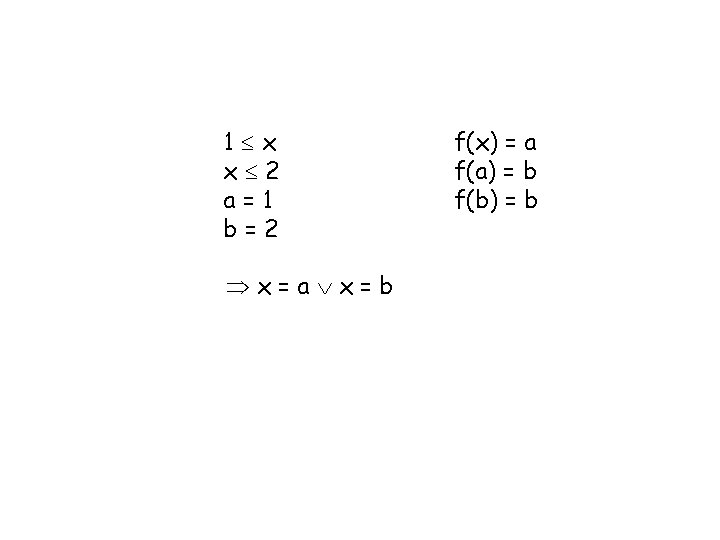
1 x x 2 a=1 b=2 x=a x=b f(x) = a f(a) = b f(b) = b

a=b 4, 3, x = b 1 x x 2 a=1 b=2 x=a a=b Unsatisfiable f(x) = a f(a) = b f(b) = b x=a

a=b 1 x x 2 a=1 b=2 x=b a=b Unsatisfiable f(x) = a f(a) = b f(b) = b x=b

The procedure returns satisfiable only when (1) C 1 is consistent (2) C 2 is consistent (3) C 1 is convex (4) C 2 is convex (5) C 1 entails (x = y) iff C 2 entails (x = y) Theorem: If the procedure returns satisfiable, then there is a model of C 1 C 2. Technical side conditions: (1) Every consistent formula in T 1 has a countably infinite model (2) Every consistent formula in T 2 has a countably infinite model

Proof Partition variables into equivalence classes Q 1, …, Qn such that for all i [1, n], if x, y Qi then C 1 entails x = y. Lemma: For all i [1, n], if x, y Qi then C 2 entails x = y. For each i [1, n], pick representative wi Qi. Lemma: C 1 Lemma: C 2 1 i < j n(wi wj) is consistent.

Proof continued D 2 = C 2 D 1 = C 1 1 i < j n(wi wj ) D 1 has a countably infinite model (U 1, I 1) D 2 has a countably infinite model (U 2, I 2) Pick an isomorphism K from U 1 to U 2 that is consistent with variable assignments, i. e. , for all x, K(I 1(x)) = I 2(x). The interpretations of function and relation symbols can be mapped easily using K.