definition of a parallelogram opposite sides of parallelogram



- Slides: 15

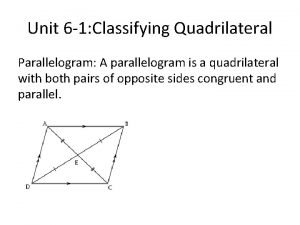
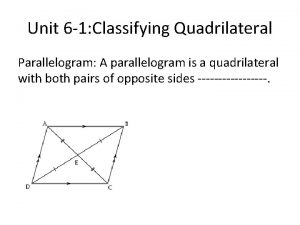
definition of a parallelogram opposite sides of parallelogram are congruent opposite angles of a parallelogram are congruent diagonals of a parallelogram bisect each other alternate interior angles theorem consecutive interior angles theorem alternate interior angles theorem converse consecutive interior angles theorem converse definition of a rhombus

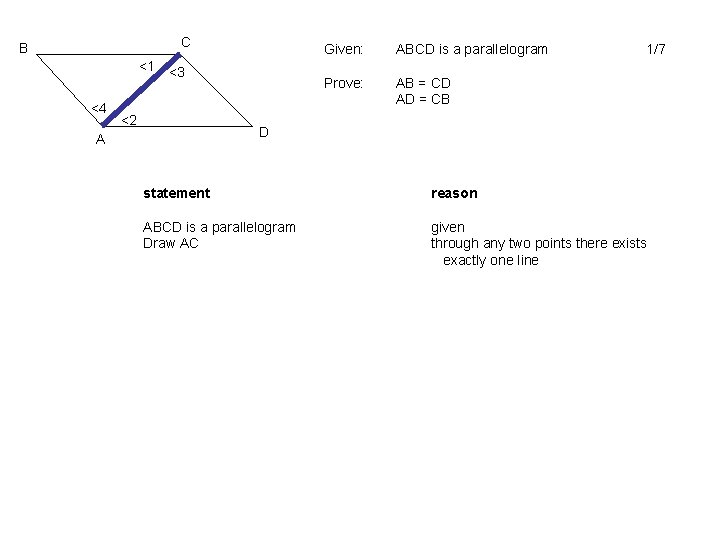
C B <1 <4 <3 <2 Given: ABCD is a parallelogram Prove: AB = CD AD = CB 1/7 D A statement reason ABCD is a parallelogram Draw AC given through any two points there exists exactly one line

C B <1 <4 <3 <2 Given: ABCD is a parallelogram Prove: AB = CD AD = CB D A statement reason ABCD is a parallelogram Draw AC given through any two points there exists exactly one line definition of a parallelogram alternate interior angles theorem reflexive property ASA CPCTC BC // DA AB // CD <1 = <2 <3 = <4 AC = AC ∆ABC = ∆CDA AB = CD AD = CB

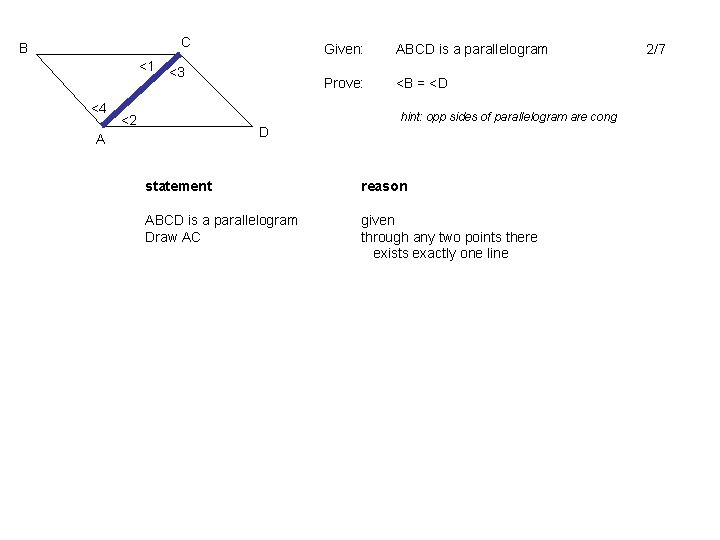
C B <1 <4 <3 Given: ABCD is a parallelogram Prove: <B = <D hint: opp sides of parallelogram are cong <2 D A statement reason ABCD is a parallelogram Draw AC given through any two points there exists exactly one line 2/7

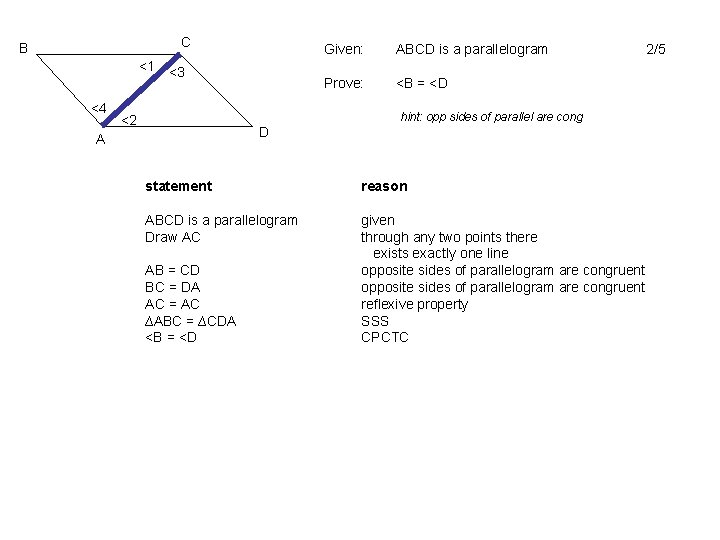
C B <1 <4 <3 Given: ABCD is a parallelogram Prove: <B = <D hint: opp sides of parallel are cong <2 D A statement reason ABCD is a parallelogram Draw AC given through any two points there exists exactly one line opposite sides of parallelogram are congruent reflexive property SSS CPCTC AB = CD BC = DA AC = AC ∆ABC = ∆CDA <B = <D 2/5

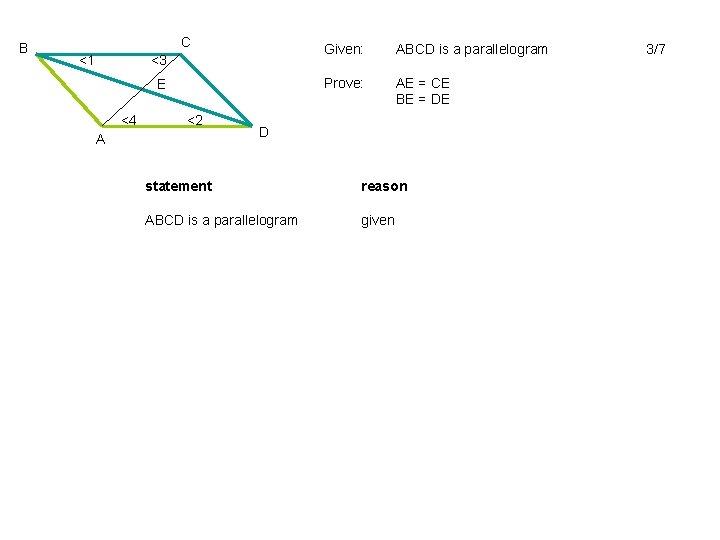
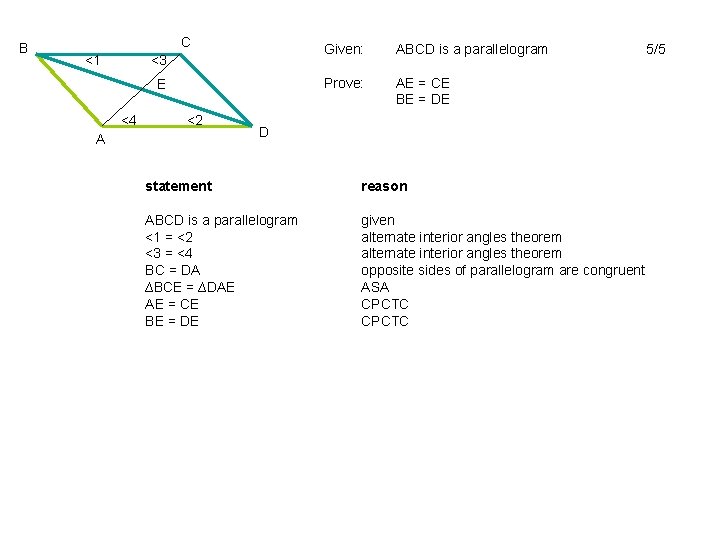
B C <1 <3 E <4 <2 A Given: ABCD is a parallelogram Prove: AE = CE BE = DE D statement reason ABCD is a parallelogram given 3/7

B C <1 <3 E <4 <2 A Given: ABCD is a parallelogram Prove: AE = CE BE = DE D statement reason ABCD is a parallelogram <1 = <2 <3 = <4 BC = DA ∆BCE = ∆DAE AE = CE BE = DE given alternate interior angles theorem opposite sides of parallelogram are congruent ASA CPCTC 5/5

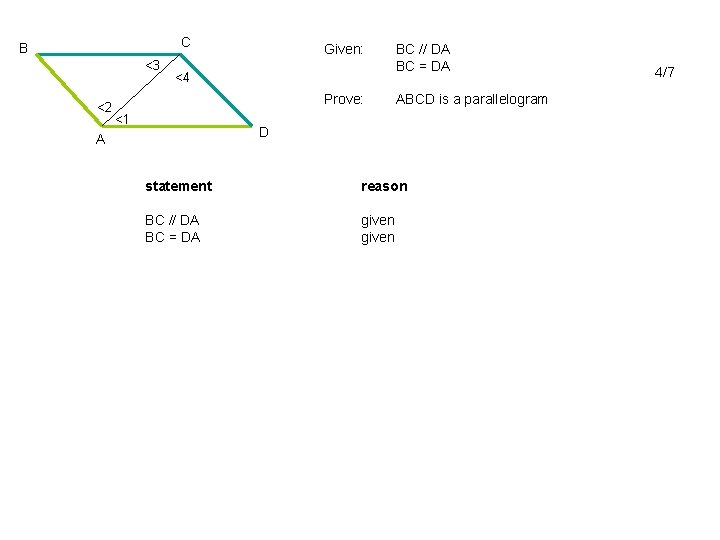
C B <3 <2 Given: <4 Prove: <1 BC // DA BC = DA ABCD is a parallelogram D A statement reason BC // DA BC = DA given 4/7

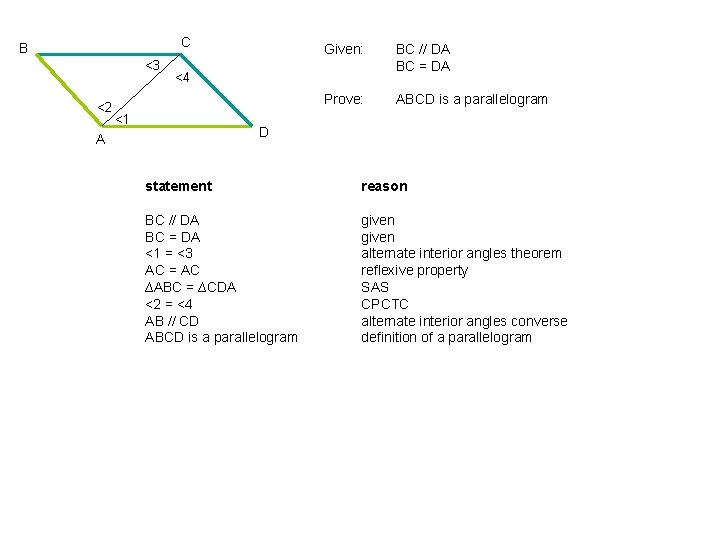
C B <3 <2 Given: BC // DA BC = DA Prove: ABCD is a parallelogram <4 <1 D A statement reason BC // DA BC = DA <1 = <3 AC = AC ∆ABC = ∆CDA <2 = <4 AB // CD ABCD is a parallelogram given alternate interior angles theorem reflexive property SAS CPCTC alternate interior angles converse definition of a parallelogram

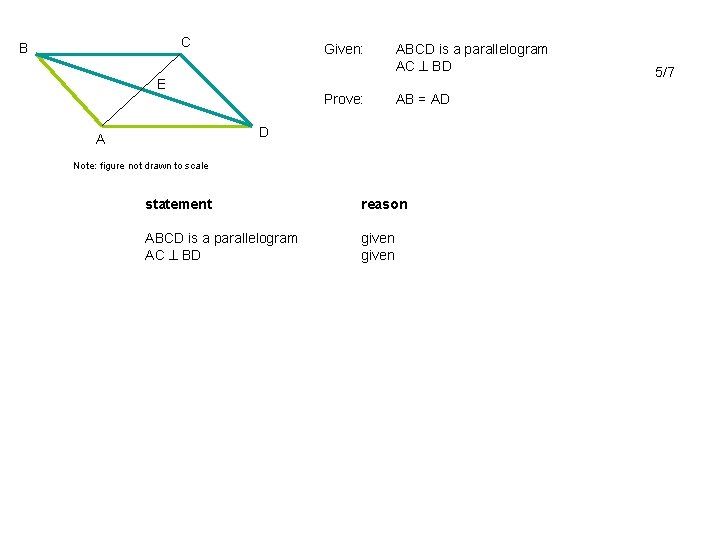
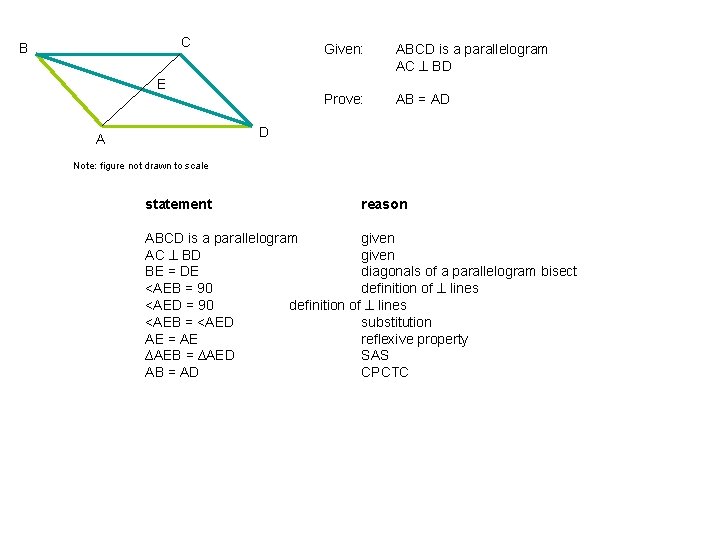
C B Given: E Prove: ABCD is a parallelogram AC BD AB = AD D A Note: figure not drawn to scale statement reason ABCD is a parallelogram AC BD given 5/7

C B E Given: ABCD is a parallelogram AC BD Prove: AB = AD D A Note: figure not drawn to scale statement reason ABCD is a parallelogram given AC BD given BE = DE diagonals of a parallelogram bisect <AEB = 90 definition of lines <AED = 90 definition of lines <AEB = <AED substitution AE = AE reflexive property ∆AEB = ∆AED SAS AB = AD CPCTC

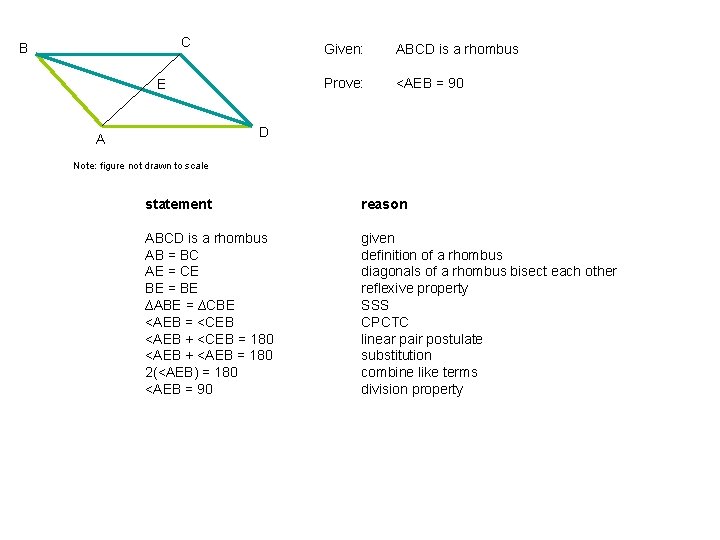
C B E Given: ABCD is a rhombus Prove: <AEB = 90 D A Note: figure not drawn to scale statement reason ABCD is a rhombus given 6/7

C B E Given: ABCD is a rhombus Prove: <AEB = 90 D A Note: figure not drawn to scale statement reason ABCD is a rhombus AB = BC AE = CE BE = BE ∆ABE = ∆CBE <AEB = <CEB <AEB + <CEB = 180 <AEB + <AEB = 180 2(<AEB) = 180 <AEB = 90 given definition of a rhombus diagonals of a rhombus bisect each other reflexive property SSS CPCTC linear pair postulate substitution combine like terms division property

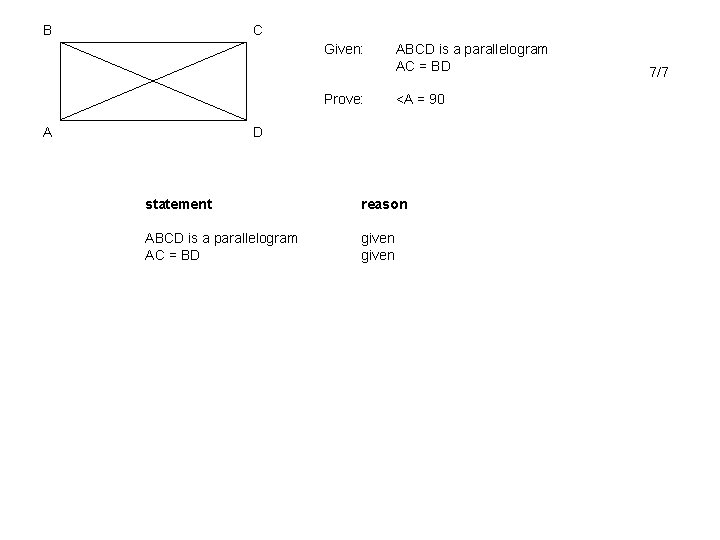
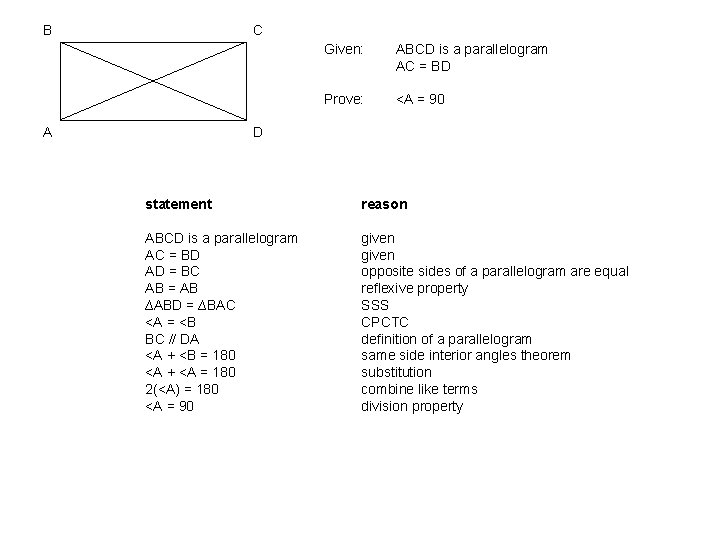
B C Given: Prove: A ABCD is a parallelogram AC = BD <A = 90 D statement reason ABCD is a parallelogram AC = BD given 7/7

B C A Given: ABCD is a parallelogram AC = BD Prove: <A = 90 D statement reason ABCD is a parallelogram AC = BD AD = BC AB = AB ∆ABD = ∆BAC <A = <B BC // DA <A + <B = 180 <A + <A = 180 2(<A) = 180 <A = 90 given opposite sides of a parallelogram are equal reflexive property SSS CPCTC definition of a parallelogram same side interior angles theorem substitution combine like terms division property
 Proving the parallelogram side theorem
Proving the parallelogram side theorem Prove eq. eq
Prove eq. eq Vertically opposite angles are
Vertically opposite angles are Describing supplementary angle relationships
Describing supplementary angle relationships Stonehenge easter island
Stonehenge easter island Campsites f and g are on opposite sides of the lake
Campsites f and g are on opposite sides of the lake M<1
M<1 Rhombusa
Rhombusa Every square is a rhombus
Every square is a rhombus Why is a square a special rectangle
Why is a square a special rectangle Definition of opposite rays
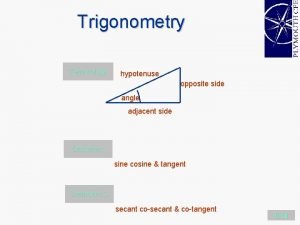
Definition of opposite rays Opposite adjacent and hypotenuse
Opposite adjacent and hypotenuse Integers essential questions
Integers essential questions Adding and subtracting integers song
Adding and subtracting integers song Performer culture and literature 3
Performer culture and literature 3 Cold opposite warm same
Cold opposite warm same