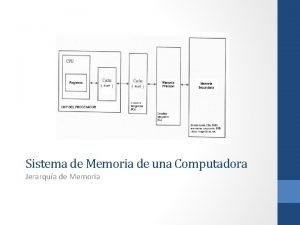
Arquitectura de Computadoras Sistemas de Representacin Ing Prof

Arquitectura de Computadoras Sistemas de Representación Ingº Prof. Alberto Omar Spinsanti

Sistemas de Representación Ø Informática = INFORmación + auto. MÁTICA Ø Estudia aspectos relacionados con la información adquisición representación tratamiento transmisión mediante ordenadores Ø Información: “conjunto de símbolos que represente hechos, objetos o ideas” números, palabras, matrículas de coche, resultados de juegos olímpicos, características climatológicas de una región, etc Ingº Prof. Alberto Omar Spinsanti 2

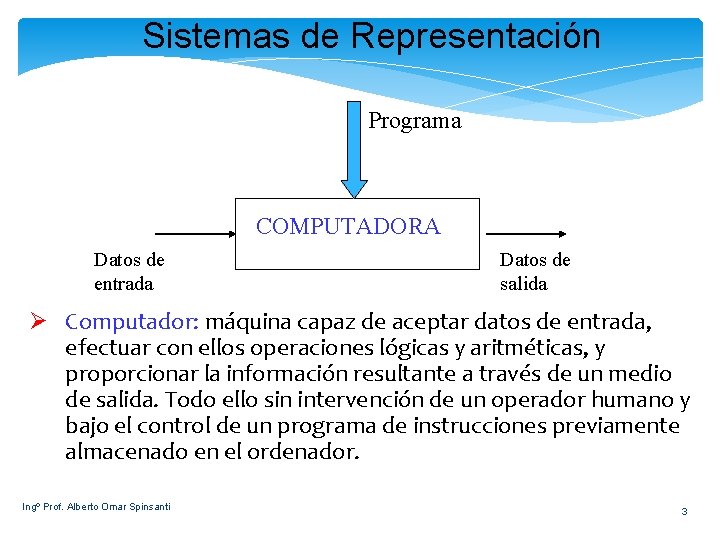
Sistemas de Representación Programa COMPUTADORA Datos de entrada Datos de salida Ø Computador: máquina capaz de aceptar datos de entrada, efectuar con ellos operaciones lógicas y aritméticas, y proporcionar la información resultante a través de un medio de salida. Todo ello sin intervención de un operador humano y bajo el control de un programa de instrucciones previamente almacenado en el ordenador. Ingº Prof. Alberto Omar Spinsanti 3

Sistemas de Representación Ø Datos: conjuntos de símbolos utilizados para expresar o representar un valor numérico, hecho, idea. . . Texto Número (0 -9) Imagen Audio Vídeo Ø Multimedia. . . para definir información que contiene números, texto, imágenes, audio y video Ingº Prof. Alberto Omar Spinsanti 4

Sistemas de Representación Ø Las computadoras representan todos sus datos en sistema de numeración binario. Ø Los datos viajan, se procesan y se almacenan en las computadoras a través de impulsos eléctricos. Estos impulsos se representan por dos estados: ü Prendido o apagado = 1 ó 0 Ingº Prof. Alberto Omar Spinsanti 5

Sistemas de Representación Ø Las computadoras almacenan datos e instrucciones en memoria. Para ello utilizan el sistema binario. Ø Razones: ü El dispositivo se encuentra en uno de dos estados posibles (0 ó 1). ü Identificar el estado es más fácil si sólo hay dos. Ø Ejemplo: ü Lámpara encendida ó apagada. ü Lámpara encendida con 10 intensidades distinta, Ø Para saber si está encendida es más fácil en el primer caso que determinar alguna de las 10 intensidades distintas. Ingº Prof. Alberto Omar Spinsanti 6

Sistemas de Representación Unidades de medida para almacenamiento de datos Ø Los computadores comprenden el lenguaje de los números Ø La organización de un computador depende entre otros factores del sistema de representación numérica adoptado Ø Se trabaja con el sistema binario, de donde proviene los términos: Bit: Acrónimo de Binary Digit (Dígito binario), es la mínima unidad de información que viaja y se almacena en un computador. Cada bit representa un impulso eléctrico (1 ó 0). Ingº Prof. Alberto Omar Spinsanti 7

Sistemas de Representación Unidades de medida para almacenamiento de datos-¿Cuántos bits usar? Si sumamos todos los símbolos que conocemos: Números+letras+caracteres raros+signos de puntuación… …. . aprox. 150 Con 7 bits = 128 estados. Corto Con 8 bits = 256 estados. OK Para representar 1 carácter se utilizan 8 bits y a esta agrupación se le llama BYTE. 1 carácter = 1 byte = 8 bits Byte: Acrónimo de Binary Term (Término binario), es un grupo de 8 bits que el computador utiliza para representar cada símbolo o carácter que conocemos, es decir un número, una letra, un signo de puntuación, etc. Con un byte, el computador puede representar 256 símbolos o caracteres diferentes. Ingº Prof. Alberto Omar Spinsanti 8

Sistemas de Representación Sistema de numeración decimal También llamado sistema de numeración Base 10, utiliza diez dígitos para representar cualquier cifra. Ellos son: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Combinando estos dígitos, podemos construir cualquier número. Ejemplo: El número 348 es un dato representado en sistema de numeración decimal. Lo construimos mediante: 3 x 102 + 4 x 101 + 8 x 100 = 300 + 40 + 8 = 348 Centena Ingº Prof. Alberto Omar Spinsanti Decena Unidad 9

Sistemas de Representación Ø En un sistema de numeración posicional de base b, la representación de un número se define a partir de la regla: № = (. . . a 3 a 2 a 1 a 0. a-1 a-2 a-3 …)b= = ……+ a 2 b 2+ a 1 b 1+ a 0 b 0+ a-1 b-1+ a-2 b-2+ a-3 b-3+ ……. . ü Donde b es un entero no negativo mayor a 1 y cuando los ai pertenecen al conjunto de enteros en el rango 0 ≤ai< b ü El punto que aparece entre los dígitos a 0 y a-1 se denomina punto fraccionario. ü Cuando b = 10 se lo llama punto decimal y cuando b = 2, punto binario. Ingº Prof. Alberto Omar Spinsanti 10

Sistemas de Representación Ø Sistema Decimal: Es el sistema de numeración utilizado en la vida cotidiana, cuya base es diez, utilizando los símbolos 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9. Ø Sistema Binario: los dos símbolos utilizados son el 0 y el 1, los que reciben el nombre de bit (Binary Digit). Ø Sistema Octal: de base 8, los símbolos utilizados son 0, 1, 2, 3, 4, 5, 6, 7. Ø Sistema Hexadecimal: de base 16, los símbolos utilizados son 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F Ingº Prof. Alberto Omar Spinsanti 11

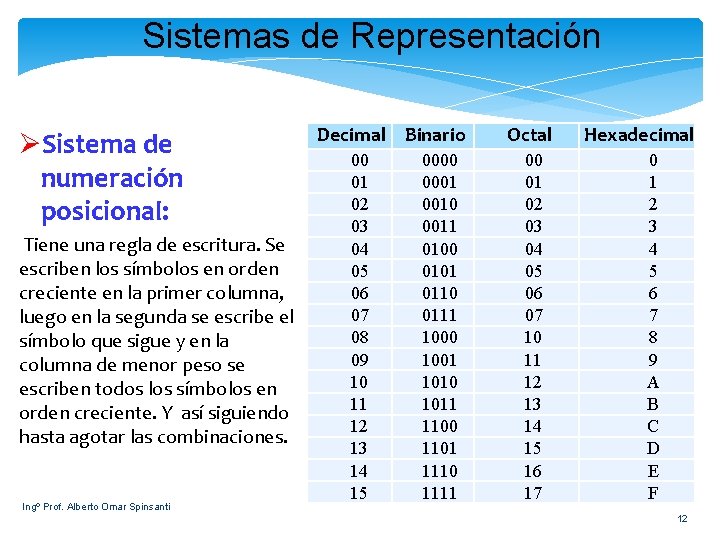
Sistemas de Representación ØSistema de numeración posicional: Tiene una regla de escritura. Se escriben los símbolos en orden creciente en la primer columna, luego en la segunda se escribe el símbolo que sigue y en la columna de menor peso se escriben todos los símbolos en orden creciente. Y así siguiendo hasta agotar las combinaciones. Ingº Prof. Alberto Omar Spinsanti Decimal Binario 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 Octal 00 01 02 03 04 05 06 07 10 11 12 13 14 15 16 17 Hexadecimal 0 1 2 3 4 5 6 7 8 9 A B C D E F 12

Sistemas de Representación Sistema de numeración binario Ø También llamado sistema de numeración Base 2, utiliza dos dígitos para representar cualquier cifra. Ellos son: 0, 1 Ø Combinando estos dígitos, podemos construir cualquier número. ü Ejemplo: El número 1100 1101 es un dato representado en sistema de numeración binario. Ingº Prof. Alberto Omar Spinsanti 13

Sistemas de Representación Sistema Binario y Hexadecimal Ø Base 2. Dígitos {0, 1} Ejemplo: 101, 1)2 = 100 + 1 + 0, 1 = 10 x 102 + 0 x 101 + 1 x 100 + 1 x 10 -1 Ø Base 16. Ejemplo: Dígitos {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F} 3 A, C)16 = 3 x 101 + A x 100 + C x 10 -1 Ingº Prof. Alberto Omar Spinsanti 14

Sistemas de Representación Sistemas Posicionales Ingº Prof. Alberto Omar Spinsanti 15

Sistemas de Representación Conversión de decimal a binario Ø Parte entera del número binario : Se obtiene por dividir sucesivamente entre 2, y después, tomar el último cociente y todos los restos en orden inverso a como han aparecido (que serán siempre ceros y unos) son las cifras binarias El último cociente será el bit más significativo y el primer resto el bit menos significativo (más a la derecha). Por lo tanto, el número 18 (en sistema decimal) equivale al número 1 0 0 1 0 (en sistema binario) Ingº Prof. Alberto Omar Spinsanti 16

Sistemas de Representación Conversión de decimal a binario Ø La parte fraccionaria del número binario: Se obtiene multiplicando por 2 sucesivamente la parte fraccionaria del número decimal de partida y las partes fraccionarias que se van obteniendo en los productos sucesivos. El número binario se forma con las partes enteras (que serán ceros y unos) de los productos obtenidos Transformar a binario natural el número decimal 0. 1875 *2 ----0. 3750 *2 -----0. 7500 *2 -----1. 5000 0. 5000 *2 -----1. 0000 0. 1875)10 = 0. 0011)2 Ingº Prof. Alberto Omar Spinsanti 17

Sistemas de Representación Conversión de decimal a binario Ejemplo: Transformar a binario el número decimal 26. 42)10 a) Parte entera: 26 | 2_ 0 13 | 2__ 1 6 | 2__ 0 3 | 2_ 1 1 | 2__ 1 0 b) Parte fraccionaria: 0. 42 0. 84 0. 68 0. 36 0. 72 *2 *2 *2 --------- ----0. 84 1. 68 1. 36 0. 72 1, 44 26, 42)10 = 11010, 01101. . . )2 Ingº Prof. Alberto Omar Spinsanti 18

Sistemas de Representación Conversión de decimal a octal La parte entera se divide por 8 y se toman los restos en sentido inverso y la parte fraccionaria se obtiene multiplicando por 8. Ejemplo: Transformar a octal el número decimal 26. 42)10 a) Parte entera: 26 | 8_ 2 3 | 8__ 3 0 b) Parte fraccionaria: 0. 42 0. 36 0. 88 0. 04 *8 *8 ---------3. 36 2. 88 7. 04 0. 32 26. 42)10 = 32, 3270. . . )8 Ingº Prof. Alberto Omar Spinsanti 19

Sistemas de Representación Conversión de decimal a Hexadecimal La parte entera se divide por 16 y se toman los restos en sentido inverso y la parte fraccionaria se obtiene multiplicando por 16 e ir tomando el № de la parte entera. Ejemplo: Transformar a Hexadecimal el número decimal 26. 42)10 a) Parte entera: 26 | 16_ 10 1 | 16__ 1 0 b) Parte fraccionaria: 0. 42 0. 72 0. 52 *16 *16 ---------6. 72 11. 52 8. 32 26. 42)10 = 1 A, 6 B 8. . . )16 Ingº Prof. Alberto Omar Spinsanti 20

Sistemas de Representación Conversión a decimal Se aplica el teorema fundamental de los números ( Sumatorias de términos) luego se remplazan los símbolos por su equivalente en el sistema decimal, se realiza la operación dando por resultado el número equivalente en el sistema decimal Conversión de Binario a Decimal Ej. : El número 11010, 011)2 en sistema binario equivale a: 1 x 10100 + 1 x 1011 + 0 x 1010 + 1 x 101 + 0 x 100 + 0 x 10 -1 + 1 x 10 -10 + 1 x 10 -11)2 = 1 x 24 + 1 x 23 + 0 x 22 + 1 x 21 + 0 x 20 + 0 x 2 -1 + 1 x 2 -2 + 1 x 2 -3)10 = 16 +8+ 0 + 2 + 0 +0+1/4+1/8)10 = 26, 37)10 en sistema decimal. Ingº Prof. Alberto Omar Spinsanti 21

Sistemas de Representación Conversión a decimal Conversión de Octal a Decimal Ej. : El número 32, 32)8 en sistema Octal equivale a: 3 x 101 + 2 x 100 + 3 x 10 -1 + 2 x 10 -2)8 = 3 x 81 + 2 x 80 + 3 x 8 -1 + 2 x 8 -2)10 = 24 +2 +3/8+2/64)10 =26, 40)10 en sistema decimal. Conversión de Hexadecimal a Decimal Ej. : El número 1 A, 6 B)16 en sistema Hexadecimal equivale a: 1 x 101 + A x 100 + 6 x 10 -1 + B x 10 -2)16 = 1 x 161 + 10 x 160 + 6 x 16 -1 + 11 x 16 -2)10 = 16 +10+6/16+11/256)10 = =26, 41)10 Ingº Prof. Alberto Omar Spinsanti en sistema decimal. 22

Sistemas de Representación Para el pasaje de una Base a otra en Forma Directa (8 2 16) es necesario poder pasar de binario a decimal en forma mental en tres bits y cuatro bits. Ejemplo: el 110) b 1010)b 4 2 1 8 4 2 1 22 21 20 23 22 21 20 1 1 0 1 0 4 + 2 0 8 + 0 6 + + 2 + 0 10 Sumamos las casillas que tienen 1 e ignoramos las que tienen 0 se obtiene el Decimal Ingº Prof. Alberto Omar Spinsanti 23

Sistemas de Representación Conversión de Binario a Octal por Agrupación El pasaje de 2 a 8 o 16, o el pasaje en sentido contrario, se puede realizar en forma mecánica, sin necesidad de realizar ningún cálculo. Cuando una base es potencia de otra ( ya sea en forma positiva o en forma negativa ) por ejemplo lo son las bases 8 y 2 ( 8 = 23 ) se reemplaza cada dígito por su equivalente numérico de la segunda Demostración para el pasaje de base 2 a 8. N)b = 110 101, 110 )2 = = 1 x 25 + 1 x 24 + 0 x 23 =[ 1 x 22 +1 x 21 + 0 x 20 ]23 = [ 4 + 2 + 0 ] 23 = 6 x 81 = 6 + 1 x 22 + 0 x 21 + 1 x 20 + [1 x 22 +0 x 21 +1 x 20 ] 20 + [ 4 + 0 + 1 ] 20 + 5 x 80 + 1 x 2 -1 + 1 x 2 -2 + 0 x 2 -3 + [1 x 22+1 x 21+ 0 x 20 ]2 -3 + [ 4 + 2 + 0 ] 2 -3 + 6 x 8 -1 5 , 6 )8 Ingº Prof. Alberto Omar Spinsanti 24

Sistemas de Representación Conversión de Binario a Hexadecimal Por agrupación 0110 1101 0010 , 0101 1010 6 D 2 , 5 A 0010 ] 2 2] 16 Conversión de Hexadecimal a Binario Por agrupación A 2 , 1 7 ] 16 1010 0010 , 0001 0111 ]2 Ingº Prof. Alberto Omar Spinsanti 25

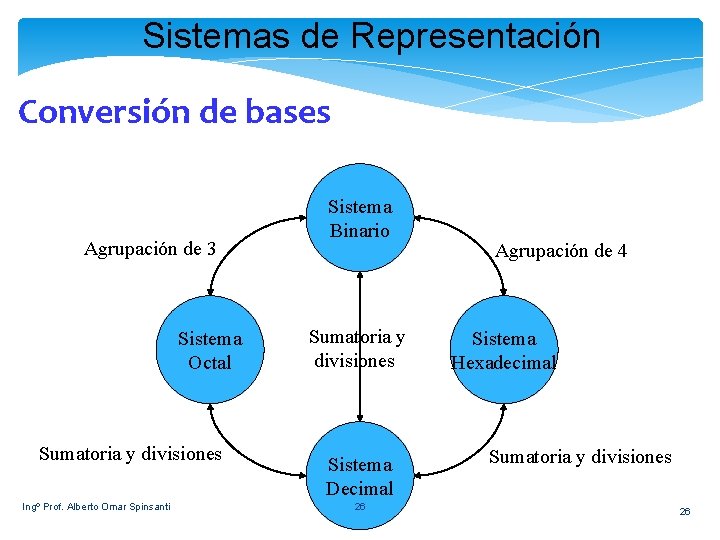
Sistemas de Representación Conversión de bases Agrupación de 3 Sistema Octal Sumatoria y divisiones Ingº Prof. Alberto Omar Spinsanti Sistema Binario Sumatoria y divisiones Sistema Decimal 26 Agrupación de 4 Sistema Hexadecimal Sumatoria y divisiones 26

Sistemas de Representación Aritmética binaria Ø Una computadora digital consume la mayor parte de su vida útil a la realización de operaciones de aritmética binaria. Ø Las reglas de la aritmética binaria son similares a las de la aritmética decimal. Los conceptos de acarreo y préstamo, por ejemplo, se aplican también a la aritmética binaria. Ingº Prof. Alberto Omar Spinsanti 27

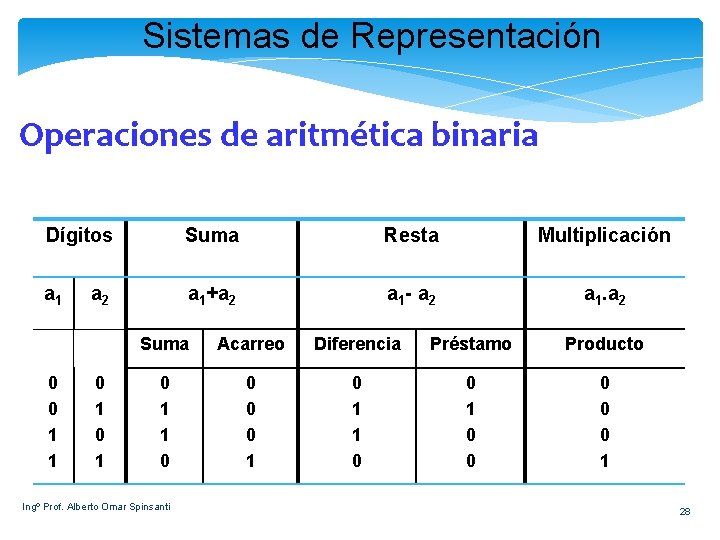
Sistemas de Representación Operaciones de aritmética binaria Dígitos Suma Resta Multiplicación a 1+a 2 a 1 - a 2 a 1. a 2 0 0 1 1 a 2 0 1 Suma Acarreo Diferencia Préstamo Producto 0 1 1 0 0 1 0 1 1 0 0 0 0 0 1 Ingº Prof. Alberto Omar Spinsanti 28

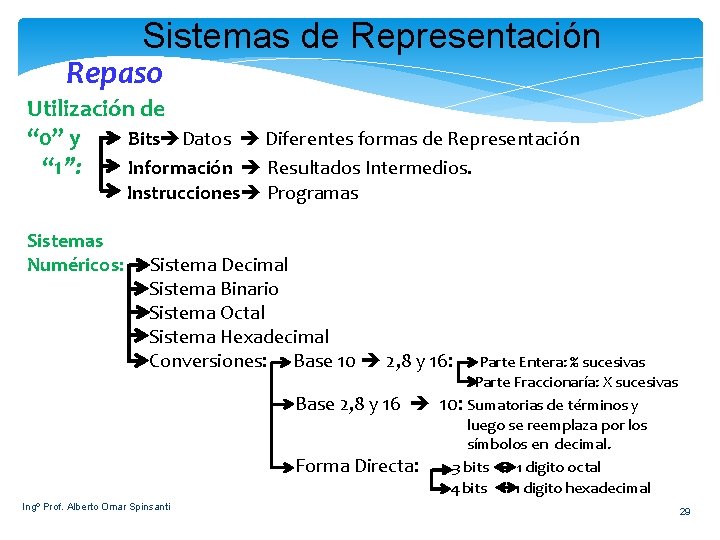
Sistemas de Representación Repaso Utilización de “ 0” y Bits Datos Diferentes formas de Representación “ 1”: Información Resultados Intermedios. Instrucciones Programas Sistemas Numéricos: Sistema Decimal Sistema Binario Sistema Octal Sistema Hexadecimal Conversiones: Base 10 2, 8 y 16: Base 2, 8 y 16 Forma Directa: Ingº Prof. Alberto Omar Spinsanti Parte Entera: % sucesivas Parte Fraccionaría: X sucesivas 10: Sumatorias de términos y luego se reemplaza por los símbolos en decimal. 3 bits 1 digito octal 4 bits 1 digito hexadecimal 29

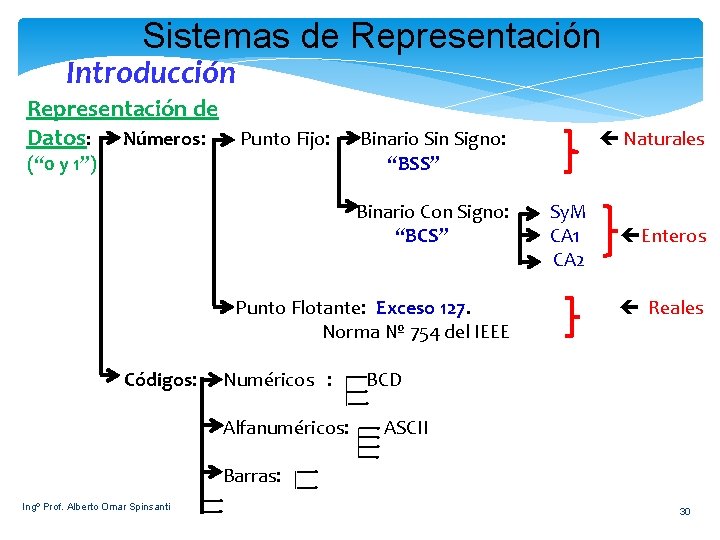
Sistemas de Representación Introducción Representación de Datos: Números: Punto Fijo: (“ 0 y 1”) Binario Sin Signo: “BSS” Binario Con Signo: “BCS” Punto Flotante: Exceso 127. Norma № 754 del IEEE Códigos: Numéricos : Alfanuméricos: Naturales Sy. M CA 1 CA 2 Enteros Reales BCD ASCII Barras: Ingº Prof. Alberto Omar Spinsanti 30

Sistemas de Representación Números sin signo “BSS” Si el número tiene n bits, puedo representar ü 2 n = números distintos El rango va desde ü 0 a (2 n– 1) Ejemplo: n = 3 bits Decimal 0 1 2 …. . . 7 Ingº Prof. Alberto Omar Spinsanti Representación signo 000 001 010 …. . . . 111 Ejemplo: n = 8 bits Decimal Binario 0. . 128. . 254 255 0000. . . 1000 0000. . . 1111 1110 1111 31

Sistemas de Representación Números sin signo “BSS” Matemáticamente para cualquier base podemos expresar esto: Número mínimo = 0 Número máximo= 10 n— 1 Rango = 10 n En Binario y Sin Signo (BSS) según la cantidad de bits tenemos Con 4 bits puedo representar 16 números y el 15 es el mayor. Con 8 bits puedo representar 256 números y el 255 es el mayor. Con 10 bits puedo representar 1. 024 números y el 1. 023 es el mayor. Con 12 bits puedo representar 4. 096 números y el 4. 095 es el mayor. Con 16 bits puedo representar 65. 536 números y el 65. 535 es el mayor. Con 32 bits puedo representar 4. 294. 967. 296 números y el 4. 294. 967. 295 es el mayor. Con 64 bits puedo representar 18. 446. 744. 073. 709. 551. 616 números y el … 615 es el mayor Ingº Prof. Alberto Omar Spinsanti 32

Sistemas de Representación de números con signo “BCS” Ø Con n bits, 1 bit representa al signo y n-1 bits a la magnitud bn-1 Signo bn-2 b 0 Magnitud Ø El bit n-1 (extremo izquierdo) representa sólo al signo Ø Los bits 0 a n-2 la magnitud ü Un 0 en el bit de signo indica que el número es positivo ü Un 1 en el bit de signo indica que el número es negativo ü Los bits 0 a n-2 representan el valor absoluto en binario ü El rango: depende de la convención (Sy. M, Ca 1 ó Ca 2) Ingº Prof. Alberto Omar Spinsanti 33

Sistemas de Representación Convención Signo y Modulo Ø Un 0 en el bit de signo indica que el número es positivo Ø Un 1 en el bit de signo indica que el número es negativo Ø Los bits 0 n-2 representan el valor absoluto en binario Ø El rango: -(2 n-1– 1) +(2 n-1– 1) Ø Hay dos ceros Ø Números distintos: 2 n Ingº Prof. Alberto Omar Spinsanti 34

Sistemas de Representación Convención Signo y Modulo Ø Ejemplo: + - ü + 510 = 0000 0101 5 ü +2510= 0001 1001 Ingº Prof. Alberto Omar Spinsanti -510= 1000 0101 5 -2510= 1001 35

Sistemas de Representación Complemento a la Base Menos Uno (Ca 1) № + CB-1 = 10 n - 1 == CB-1 = (10 n - 1) – № “n= Cantidad de Bits” Ø El complemento a la base menos uno de un №, es lo que lo falta a № para llegar a el modulo 10 n menos uno. Ø En Base 2 seda una regla práctica en donde el Ca 1 de un número se obtiene invirtiendo todos los bits, Ø Si el número es positivo, los n bits tienen la representación binaria del número (como siempre ) Ø Si el número es negativo, los n bits ü Los n bits representan al número. tienen el Ca 1 del valor deseado. Ingº Prof. Alberto Omar Spinsanti ü Los positivos empiezan con cero (0) ü Los negativos empiezan con uno (1) ü El rango: -(2 n-1– 1) a +(2 n-1– 1) con 2 cero 36

Sistemas de Representación Complemento a la Base Menos Uno (Ca 1) Ø Ejemplo: + CB-1 = (10 n - 1) – № - ü + 510 = 0000 0101 -510= 1111 1010 ü +2510= 0001 1001 -2510= 1110 0110 Ingº Prof. Alberto Omar Spinsanti 37

Sistemas de Representación Complemento a la Base Menos Uno (Ca 1) CB-1 = (10 n - 1) – № Ø Ejemplo: Dada una cadena de bits ¿qué número decimal representa si lo interpretamos en Ca 1? ü Cuando es positivo: 0000 0101 =1 x 22+ 1 x 20 = 4+1 = + 5 ü Cuando es negativo, saco el Ca 1 del número y obtengo el positivo y luego cambio el signo 1111 1010 0000 0101 = +510 1111 1010 = - 510 Ingº Prof. Alberto Omar Spinsanti 38

Sistemas de Representación Complemento a la Base (Ca 2) № + CB = 10 n - № Ø El complemento a la base de un №, es lo que lo falta a № para llegar a el modulo 10 n. Ø Otra forma: “mirando” desde la derecha se escribe el número (base 2) igual hasta el primer “ 1” uno inclusive y luego se invierten los demás dígitos Ø Los positivos empiezan con cero (0) Ø Los negativos empiezan con uno (1) Ø El rango es asimétrico y va desde - (2 n-1 ) a + (2 n-1– 1) Ø Hay un solo cero Ingº Prof. Alberto Omar Spinsanti 39

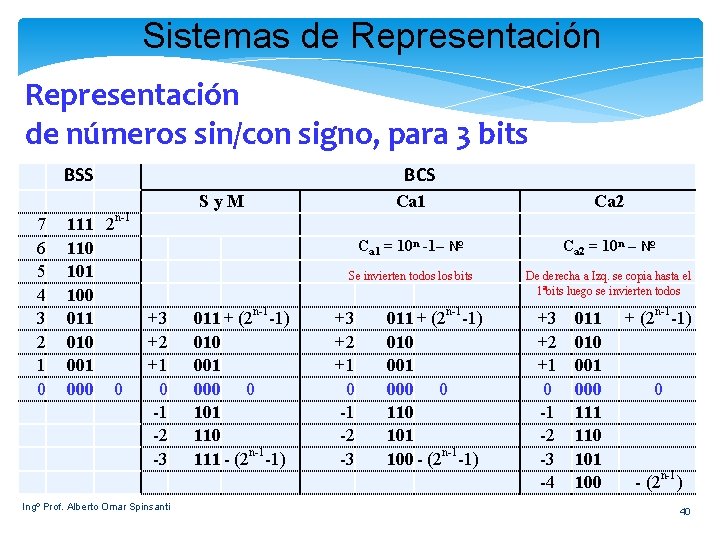
Sistemas de Representación de números sin/con signo, para 3 bits BSS 7 6 5 4 3 2 1 0 111 2 n-1 110 101 100 011 +3 010 +2 001 +1 000 0 0 -1 -2 -3 Ingº Prof. Alberto Omar Spinsanti BCS Sy. M 011 + (2 n-1 -1) 010 001 000 0 101 110 111 - (2 n-1 -1) Ca 1 Ca 2 Ca 1 = 10 n -1– № Ca 2 = 10 n – № Se invierten todos los bits De derecha a Izq. se copia hasta el 1ªbits luego se invierten todos +3 +2 +1 0 -1 -2 -3 011 + (2 n-1 -1) 010 001 000 0 110 101 100 - (2 n-1 -1) +3 +2 +1 0 -1 -2 -3 -4 011 010 001 000 111 110 101 100 + (2 n-1 -1) 0 - (2 n-1) 40

Sistemas de Representación Bits de condición (banderas) Ø Son bits que el procesador establece de modo automático acorde al resultado de cada operación realizada. Ø Sus valores permitirán tomar decisiones como: ü Realizar o no una transferencia de control. ü Determinar relaciones entre números (mayor, menor, igual). Ingº Prof. Alberto Omar Spinsanti 41

Sistemas de Representación Banderas aritméticas Ø Z(cero): vale 1 si el resultado de la operación son todos bits 0. Ø C(carry): en la suma vale 1 si hay acarreo del bit más significativo; en la resta vale 1 si hay, orrow ‟hacia el bit más significativo. ü Cuando la operación involucra números sin signo, C=1 indica una condición fuera de rango. Ø N(negativo): igual al bit más significativo del resultado. ü Es 1 si el resultado es negativo Ø V(overflow): en 1 indica una condición de fuera de rango (desborde) en BCS (Ca 2). ü El resultado no se puede expresar con el número de bits utilizado. Ingº Prof. Alberto Omar Spinsanti 42

Sistemas de Representación Suma en Ca 2 Ø Para sumar dos números en Ca 2 se suman los n bits directamente. ü Si sumamos dos números + y el resultado es – ó si sumamos dos – y el resultado es + hay overflow, en otro caso no lo hay. ü Si los № son de distinto signo nunca puede haber overflow. Ingº Prof. Alberto Omar Spinsanti 43

Sistemas de Representación Resta en Ca 2 Ø Para restar dos números en Ca 2, se restan los n bits directamente. También se puede sacar el Ca 2 el sustraendo y transformar la resta en suma. Ø Si a un № “+” le restamos un № “–” y el resultado es “–” ó si a un № “–” le restamos un “+” y el resultado es “+” hay overflow en la resta. Ø Si son del mismo signo nunca hay overflow Ingº Prof. Alberto Omar Spinsanti 44

Sistemas de Representación Bits de condición para la suma Operación + 0 1 0 0 0 1 1 S Z V C 0 0 Ca 2 Sin Signo +2 + +1 +3 2 + 1 3 Los dos resultados son correcto. Ingº Prof. Alberto Omar Spinsanti 45

Sistemas de Representación Bits de condición para la suma Operación + S Z V C 1 0 Ca 2 Sin Signo 0 1 0 +2 0 1 1 + +3 1 0 1 Overf -3 2 + 3 5 Ca 2 incorrecto, sin Signo correcto. Ingº Prof. Alberto Omar Spinsanti 46

Sistemas de Representación Bits de condición para la suma Operación 0 1 0 + 1 1 0 0 0 S Z V C 0 1 Ca 2 Sin Signo +2 + 2 -2 + 6 0 Carry 0 Ca 2 correcto, sin Signo incorrecto. Ingº Prof. Alberto Omar Spinsanti 47

Sistemas de Representación Bits de condición para la suma Operación S Z V C 0 0 1 1 Ca 2 Sin Signo 1 0 0 -4 4 + 1 1 0 + -2 + 6 1 0 Overf +2 Carry 2 Los dos resultados son incorrecto. Ingº Prof. Alberto Omar Spinsanti 48

Sistemas de Representación Bits de condición para la Resta Operación S Z V C 0 0 0 1 Ca 2 Sin Signo 1 - 0 1 0 0 1 1 1 +2 - +3 -1 2 - 3 7 Ca 2 correcto, Sin Signo incorrecto. Ingº Prof. Alberto Omar Spinsanti 49

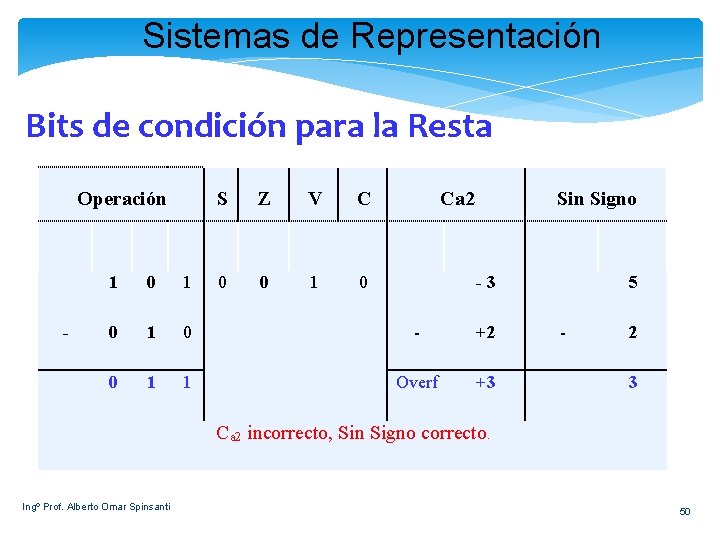
Sistemas de Representación Bits de condición para la Resta Operación - S Z V C 0 0 1 0 Ca 2 Sin Signo 1 0 1 -3 0 1 0 - +2 0 1 1 Overf +3 5 - 2 3 Ca 2 incorrecto, Sin Signo correcto. Ingº Prof. Alberto Omar Spinsanti 50

Sistemas de Representación Conversion decimal de un número en complemento a 2 Ø Para los positivos es trivial, se aplica el teorema fundamental de los numéros evaluando el polinomio que corresponda a la expresión binaria. Ø En el caso de los negativos debemos hacer el procedimiento inverso. • Se suma 1, • Se invierten los bits, • Se convierte a decimal • Se le coloca el signo “–” adelante Esto es equivalente a obtener el complemento a 1 y sumarle 1. Ingº Prof. Alberto Omar Spinsanti 51

Sistemas de Representación Resta en complemento a 10 Al tener los número negativo en el complemento a la base, las sumas y restas quedan reducidas a sumas Este sistema de representación de los negativos es de sumo interés en el caso de los ordenadores ya que al usarlo se reduce la complejidad de los circuitos ØSupongamos que se ha de realizar la siguiente operación: 77 - 63 Se puede hacer de dos formas diferentes: ü Directamente: 77 - 63 = 14 ü Utilizando el complemento a 10 del substraendo: Ø Complemento a 10 del substraendo 63 es 37 99 36 77 -63 +1 + 37 -----36 37 1 14 El 1 que salto fuera del formato no se considera. El resultado es 14 Es decir, para restar basta con sumar el minuendo con el complemento a la base del substraendo y sin considerar el acarreo Ingº Prof. Alberto Omar Spinsanti 52

Sistemas de Representación Resta en complemento a 2 Supongamos se ha de efectuar la siguiente resta: 11001 – 10010 Se puede hacer de dos formas: a) Directamente: 1 1001 -1 0010 0 0111 b) Usando el complemento a 2 del substraendo: El substraendo es 10010. Su complemento a 2 (Ca 2) se obtiene cambiando 0 por 1 y 1 por 0. 0 1101 y sumándole 1 0 1101 + 1 0 1110 Ahora sumamos al minuendo el complemento a 2 (Ca 2) del substraendo : 1 1001 + 0 1110 1 0 0111 El que sale fuera del formato no se considera. Ingº Prof. Alberto Omar Spinsanti 53

Sistemas de Representación Banderas Overflow. Tanto en la representación en Ca 1 como en Ca 2 una operación puede dar como resultado un número que excede la capacidad de la palabra de memoria, produciéndose así el overflow. Al sumar dos números el overflow se puede dar sólo si los dos tienen el mismo signo; la suma de dos números de distinto signo nunca dará como resultado un número con módulo mayor al de mayor módulo de los dados, al máximo será igual (al sumarle 0 a otro número), pero en general será menor, por lo tanto no puede exceder la capacidad de la palabra de memoria. El overflow se reconoce cuando los bits de signo de los dos números que se suman son iguales entre si pero distintos del bit de signo del resultado, o sea cuando los números son positivos y da resultado negativo o viceversa. En este caso el contenido de la palabra de memoria es incorrecta. Carry. Ocurre cuando en alguna operación se sale fuera del formato. Hay un rebalse en el bit de peso mayor. Ingº Prof. Alberto Omar Spinsanti 54

Sistemas de Representación Ejemplo de Overflow y Carry Ø Sumar 5 y 3 en representación en BSS en palabras de 3 bits. 101 representación en BSS de 5 + 011 representación en BSS de 3 1 000 Si tengo una suma en BSS y me da carry significa que el resultado es erróneo. Me da algo por afuera de lo que puedo escribir. El resultado no se puede escribir en el rango que hay. Ø Sumar 2 y 3 en representación en BCS en palabras de 3 bits. 010 representación en BCS de 2 + 011 representación en BCS de 3 101 representación en BCS (Ca 2) de -3 La suma da overflow ya que al sumar los dos positivos dio negativo. El resultado es incorrecto. Ingº Prof. Alberto Omar Spinsanti 55

Sistemas de Representación Punto Flotante Escribir los números reales en floating point en castellano punto flotante, es una convención que se utiliza para trabajar en computación con números que tengan un amplio rango, es decir para poder trabajar con números de mayor cantidad de bits que tiene la palabra de la maquina. Es semejante a la notación científica decimal, que nos permite en poco dígitos representar N° muy grande o muy chicos. Ej. : 12. 3 x 10+6 ]d o 3. 25 x 10 -8 ]d -- Nd = ± m 10 ±P Ingº Prof. Alberto Omar Spinsanti 56

Sistemas de Representación Punto Flotante Recta de los Números reales № “-” № “+” ================l================== “-” infinito 0 “+” infinito Si nuestra computadora digital tiene 2 dígitos y como trabaja con números de precisión finita y fija, podríamos trabajar con 100 combinaciones ( en el sistema decimal), esto porque nuestra maquina guarda los datos en la memoria con dos dígitos. Conjunto de números de dos dígitos: cada № se representa con un conjunto de dos dígitos 50 00 49 n ===========l===============l======== desbordamiento negativo Ingº Prof. Alberto Omar Spinsanti desbordamiento positivo 57

Sistemas de Representación Punto Flotante Si trabajaríamos con notación científica de 2 dígitos de mantisa y dos dígitos de exponente, cada № se representa con dos conjunto de dos dígitos, uno para la mantisa y otro para el exponente es como utilizamos dos lugares de memoria, en donde en cada lugar de memoria se guardan dos dígitos. Con esta forma de anotar tenemos otra diferencia mas con la recta de los № reales. Además de los desbordamiento, existe subdesbordamiento al rededor del cero : - 99. 10+99 -01. 10 -99 0 +01. 10 -99 +99. 10+99 ====l===========l=======l==========l===== desbord. ”-“ N° ”-“ utilizables subdesbordamiento N° “+” utilizables desbord. ”+” Para poder trabajar con un amplio rango se escriben № en P. F. y existen varias convenciones, nosotros veremos convención en exceso 127 o norma N° 754 del IEEE. Ingº Prof. Alberto Omar Spinsanti 58

Sistemas de Representación Punto Flotante Exceso 127 ( NORMA № 754 DE PUNTO FLOTANTE DEL IEEE) Ø Esta norma define tres formatos : precisión sencilla 32 bits, precisión doble 64 bits y precisión extendida 80 bits, nosotros solamente vemos precisión sencilla Ø Estos formatos utilizan para su escritura base dos. Ø Para la norma del Instituto de Ingenieros Electrónicos y Electricistas “IEEE” se debe tener las siguientes reglas básicas : • En precisión sencilla son representado por 32 bits (4 bytes) : 1 bit para el signo de la mantisa, 8 bits para el exponente y 23 bits para la mantisa. Ingº Prof. Alberto Omar Spinsanti 59

Sistemas de Representación Punto Flotante Exceso 127 ( NORMA N°. 754 DE PUNTO FLOTANTE DEL IEEE) La representación es en binario polarizado el exponente y normalizada la mantisa : Nº = ± 1, Mantisa. 10 C = ± 1, b 5 b 4 bn x 10 C Ø En el primer byte y el primer bit de este dará el signo de la mantisa, tratándose de representar a la fracción como un N ° del tipo signo y modulo. Ø Al exponente se lo desplaza 127, dando la característica C = 127 ±e y se anotan en los 8 bits siguientes al bits de signo. Ø La parte fraccionaria se escribe en los últimos 23 bits, sobreentendiéndose que tiene un 1, en la parte entera, que no se representa en su normalización. Solo se representa la parte fraccionaria de la mantisa. Ingº Prof. Alberto Omar Spinsanti 60

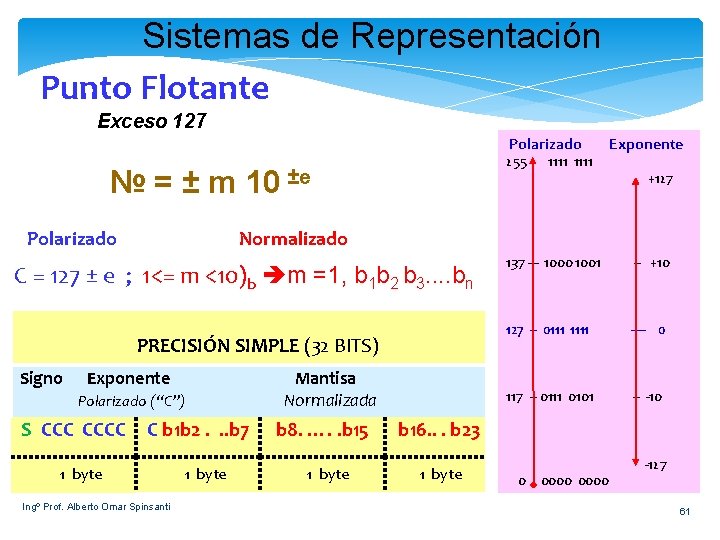
Sistemas de Representación Punto Flotante Exceso 127 Polarizado 255 № = ± m 10 ±e Polarizado PRECISIÓN SIMPLE (32 BITS) Exponente Polarizado (“C”) S CCCC +127 Normalizado C = 127 ± e ; 1<= m <10)b m =1, b 1 b 2 b 3. . bn Signo 1111 Exponente C b 1 b 2. . . b 7 1 byte Ingº Prof. Alberto Omar Spinsanti 1 byte Mantisa Normalizada b 8. …. . b 15 1 byte 137 --- 1000 1001 -- +10 127 -- 0111 1111 ---- 0 117 -- 0111 0101 -- -10 b 16. . . b 23 1 byte 0 0000 -127 61

Sistemas de Representación Punto Flotante Exceso 127 Los valores extremos que se utilizan para representar : Nos permite manejar números desde ± 38 dígitos y lograr una exactitud entre 6 y 7 dígitos: Ø con C =1111 y m=0, se representa el ± infinito según el bits de signo Ø con C= 1111 y m <>0, se indica operaciones no validas, ej. 0. infinito Ø con C=0000, m=0 y el bits de signo de valor 1 se representa el cero, Ø con C=0000 y m<>0, el № esta desnormalizado. Ø En definitiva el intervalo del exponente va de - 128 a + 127 Ingº Prof. Alberto Omar Spinsanti 62

Sistemas de Representación Códigos Binarios Estándar ØLa información por lo general es representada o transmitida por un conjunto de símbolos que unidos de una forma lógica forman un código. ØPensando de manera más general, un conjunto de símbolos constituye un alfabeto del cual estos símbolos son los dígitos. La serie de dígitos reciben el nombre de palabras. La asignación de una palabra de código a cada mensaje en un conjunto de mensajes constituye el código. ØSe puede usar el sistema binario para codificar cualquier información. Ingº Prof. Alberto Omar Spinsanti 63

Sistemas de Representación Códigos Binarios ØRegla q. El número de bits que se usará en cada palabra de código depende del número total de mensajes distintos que se van a transmitir en la información deseada § n = número de bits § Número de mensajes = 2 n ØPregunta: ¿cuántos bits necesitas para codificar a todos los integrantes de la clase de Arquitectura de Computadoras? 64 Ingº Prof. Alberto Omar Spinsanti

Sistemas de Representación Códigos Binarios La computadora no puede usar el sistema binario verdadero porque, además de representar números, debe representar caracteres alfabéticos y muchos otros símbolos que se usan en el lenguaje natural, como $ o &. Esto obligó a los fabricantes de hardware a crear códigos binarios de tipo estándar, como por ejemplo los siguientes códigos: Ø Código ASCII Ø BCD (decimal codificado en binario) Ø Códigos ponderados (8421, 5421, 2421) Ø Código Gray Ø Código de 7 segmentos Ø Códigos de Barras (detección de errores). Ingº Prof. Alberto Omar Spinsanti 65

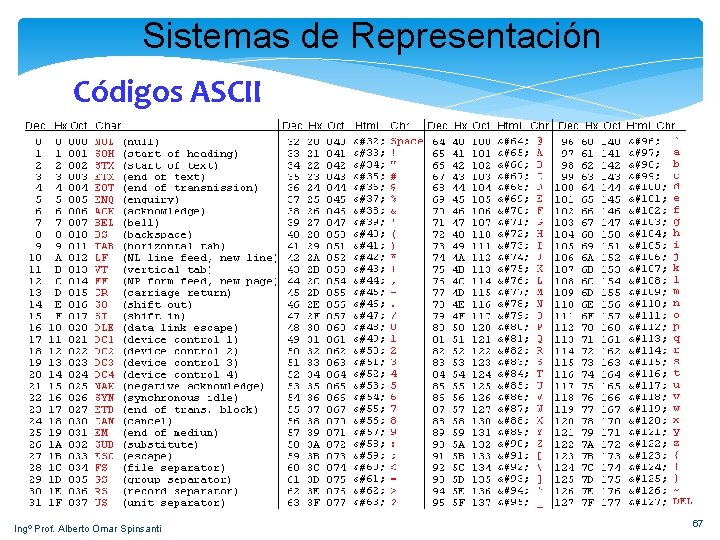
Sistemas de Representación Códigos ASCII generalmente se pronuncia "aski", es un acrónimo de American Standar Code for Information Interchange: “Código Estándar Americano para el Intercambio de Información”. Su uso primordial es facilitar el intercambio de información entre sistemas de procesamiento de datos y equipos asociados y dentro de sistemas de comunicación de datos. En un principio cada carácter se codificaba mediante 7 dígitos binarios (poniéndose el bit 8 en su estado de apagado o “O”). y fue creado para el juego de caracteres ingleses más corrientes. Ingº Prof. Alberto Omar Spinsanti 66

Sistemas de Representación Códigos ASCII Ingº Prof. Alberto Omar Spinsanti 67

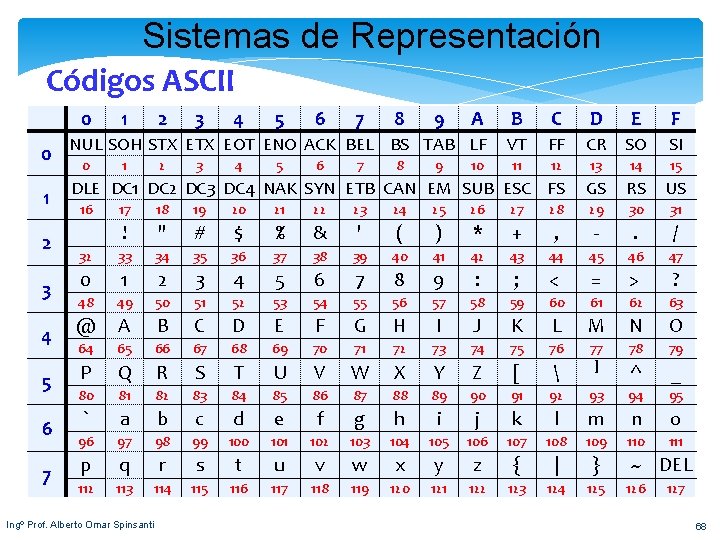
Sistemas de Representación Códigos ASCII 0 A B C D E F 0 NUL SOH STX EOT ENO ACK BEL BS TAB LF VT FF CR SO SI 11 12 13 14 15 1 DLE DC 1 DC 2 DC 3 DC 4 NAK SYN ETB CAN EM SUB ESC FS GS RS US 0 2 1 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 10 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 ! " # $ % & ' ( ) * + , - . / 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 0 1 2 3 4 5 6 7 8 9 : ; < = > ? 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 4 @ A B C D E F G H I J K L M N O 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 5 P Q R S T U V W X Y Z [ ] ^ _ 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 ` a b c d e f g h i j k l m n o 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 p q r s t u v w x y z { | } 112 113 114 115 116 117 118 119 120 121 122 123 124 125 2 3 6 7 16 1 Ingº Prof. Alberto Omar Spinsanti ~ DEL 126 127 68

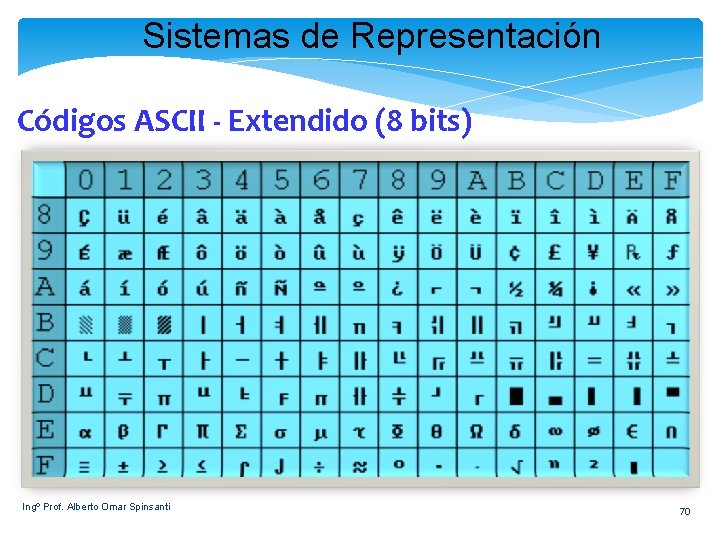
Sistemas de Representación Códigos ASCII - Extendido (8 bits) Ø Por no contemplar ni caracteres especiales ni caracteres específicos de otras lenguas el ASCII. Esto hizo que posteriormente se extendiera a 8 dígitos binarios. § De esta forma cada letra, dígito o carácter especial ocupa un byte en la memoria de la computadora. Ø Podemos observar que este método de representación de datos es muy ineficiente en el aspecto numérico, ya que en formato binario nos basta un solo byte para representar números de 0 a 255, en cambio con el código ASCII un byte puede representar únicamente un dígito numérico. § Debido a esta ineficiencia, el código ASCII es principalmente utilizado en la memoria para representar texto 69 Ingº Prof. Alberto Omar Spinsanti

Sistemas de Representación Códigos ASCII - Extendido (8 bits) Ingº Prof. Alberto Omar Spinsanti 70

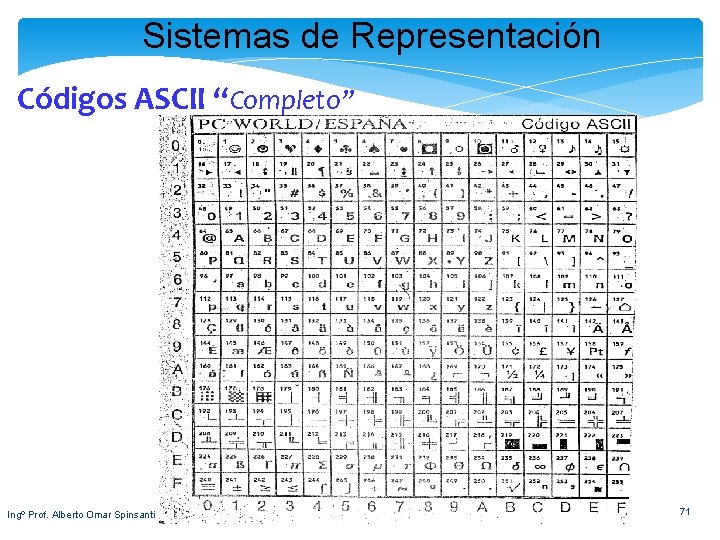
Sistemas de Representación Códigos ASCII “Completo” Ingº Prof. Alberto Omar Spinsanti 71

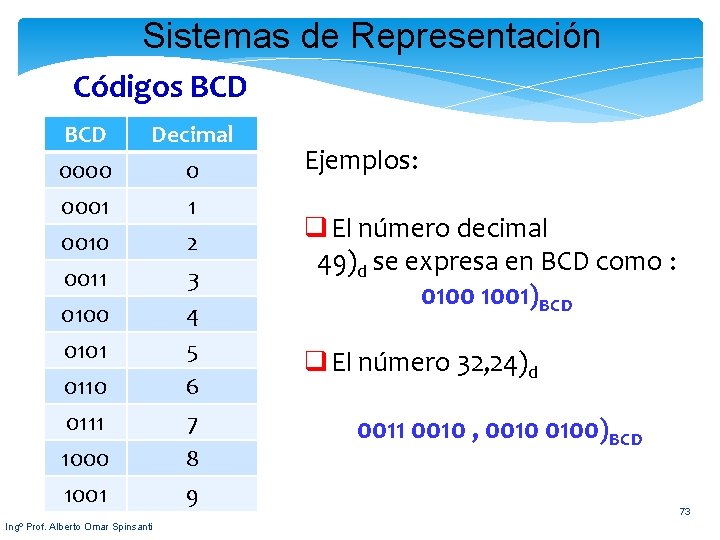
Sistemas de Representación Códigos BCD es un acrónimo de Código Binario Decimal: En esta notación se utilizan grupos de 4 bits para representar cada dígito decimal del 0 al 9. Con este método podemos representar dos dígitos por byte de información. Este método es mucho mas práctico para representación de números en la memoria en comparación al ASCII, todavía se queda por debajo del binario, ya que con un byte en el método BCD solo podemos representar dígitos del 0 al 99, en cambio, en formato binario podemos representar todos los dígitos desde 0 hasta 255. Este formato es utilizado principalmente para representar números muy grandes en aplicaciones mercantiles ya que facilita las operaciones con los mismos evitando errores de redondeo. Ingº Prof. Alberto Omar Spinsanti 72

Sistemas de Representación Códigos BCD 0000 0001 0010 Decimal 0 1 2 0011 0100 0101 0110 0111 1000 1001 3 4 5 6 7 8 9 Ingº Prof. Alberto Omar Spinsanti Ejemplos: q El número decimal 49)d se expresa en BCD como : 0100 1001)BCD q El número 32, 24)d 0011 0010 , 0010 0100)BCD 73

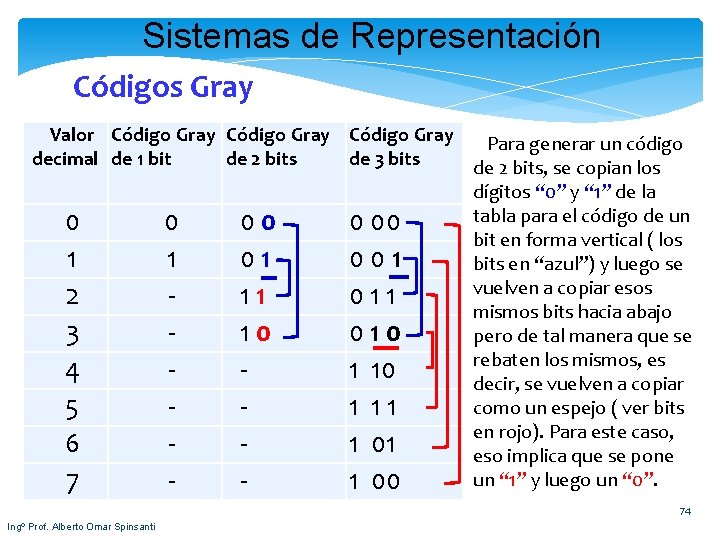
Sistemas de Representación Códigos Gray Valor Código Gray Para generar un código decimal de 1 bit de 2 bits de 3 bits de 2 bits, se copian los dígitos “ 0” y “ 1” de la tabla para el código de un 0 0 00 bit en forma vertical ( los 1 1 01 001 bits en “azul”) y luego se vuelven a copiar esos 2 11 011 mismos bits hacia abajo 3 10 010 pero de tal manera que se rebaten los mismos, es 4 1 10 decir, se vuelven a copiar como un espejo ( ver bits 5 1 11 en rojo). Para este caso, 6 1 01 eso implica que se pone un “ 1” y luego un “ 0”. 7 1 00 74 Ingº Prof. Alberto Omar Spinsanti

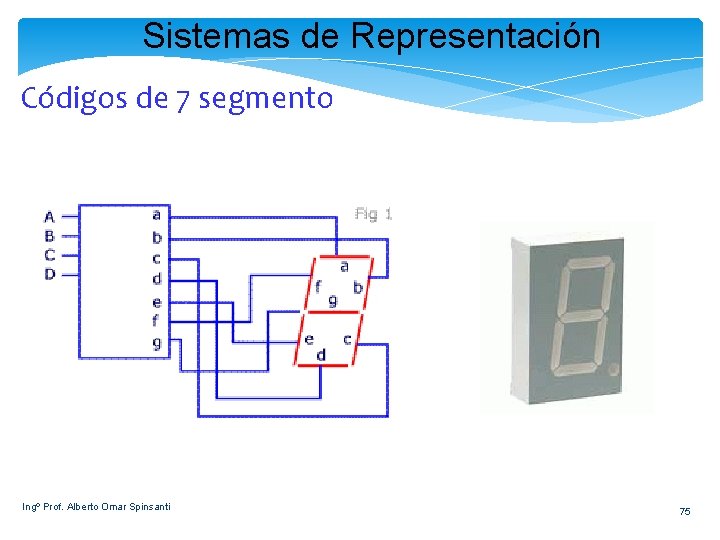
Sistemas de Representación Códigos de 7 segmento Ingº Prof. Alberto Omar Spinsanti 75

Sistemas de Representación Códigos de barras Otro caso habitual donde aparece información redundante con la finalidad de verificar errores, es en los códigos de barras, habituales en cualquier producto que se comercialice masivamente. En 1974 los 12 países que entonces formaban la Unión Europea decidieron adoptar un sistema de codificación para los productos, similar al sistema UPC de Estados Unidos de Norteamérica. Así surgió el código EAN (European Article Numbering), sistema que han adoptado más de 100 países y cerca de un millón de empresas. El más usual es EAN 13, formado por 13 dígitos agrupados en cuatro partes: prefijo, código empresa, código producto y dígito de control. El prefijo asignado por EAN internacional a AECOC es el 84, de modo que la mayoría de las empresas que forman parte del sistema EAN a través de AECOC utilizan este número. El código de empresa (fabricante o cadena de distribución) está formado por un número de entre 5 y 8 dígitos. El código del producto completa los primeros 12 dígitos y el último dígito es de control. Ingº Prof. Alberto Omar Spinsanti 76

Sistemas de Representación Códigos de barras Por ejemplo, un tarro con garbanzos cocidos marca Eroski, lleva el siguiente código 8480010021967, donde 84 significa España, 80010 es el número que tiene asignado la cooperativa Eroski, 02196 corresponde a ese tipo de garbanzos, siendo una clasificación interna del distribuidor y 7 es el código de control. En el momento de la venta, el terminal punto de venta (TPV), realiza las siguientes operaciones: 8480010021967 1. Suma los dígitos de las posiciones pares: 4+0+1+6 = 12 2. Multiplica el resultado por 3: 12 x 3= 36 3. Le añade los dígitos de las posiciones impares: 36+8+8+2+9=63 4. Resta la suma obtenida del siguiente múltiplo de 10: 70 -63=7 Si el resultado coincide con el dígito de control, como es el caso, el ordenador enviará el precio al TPV. Ingº Prof. Alberto Omar Spinsanti 77

Sistemas de Representación Unidades de medida para almacenamiento de datos – Bytes Ejemplo: Para representar el número 348 ¿Cuántos Bytes necesita nuestra computadora? El número está compuesto por 3 dígitos => Necesitamos 3 bytes 00000011 000001000 3 4 8 Ingº Prof. Alberto Omar Spinsanti 78

Sistemas de Representación Unidades de medida para almacenamiento de datos – Bytes El sistema de medición para almacenamiento de datos se fundamenta en: Ø Un Byte como medida base. Ø 1024 (210) como factor multiplicador para el incremento. Ø Los prefijos: Kilo, Mega, Giga, Tera, etc. Así: Ø 1 Kilo. Byte = 1024 Bytes Ø 1 Mega. Byte = 1024 Kilo. Bytes = 1024 x 1024 Bytes Ø 1 Giga. Byte = 1024 Mega. Bytes = 1024 x 1024 Kilo. Bytes … Ingº Prof. Alberto Omar Spinsanti 79

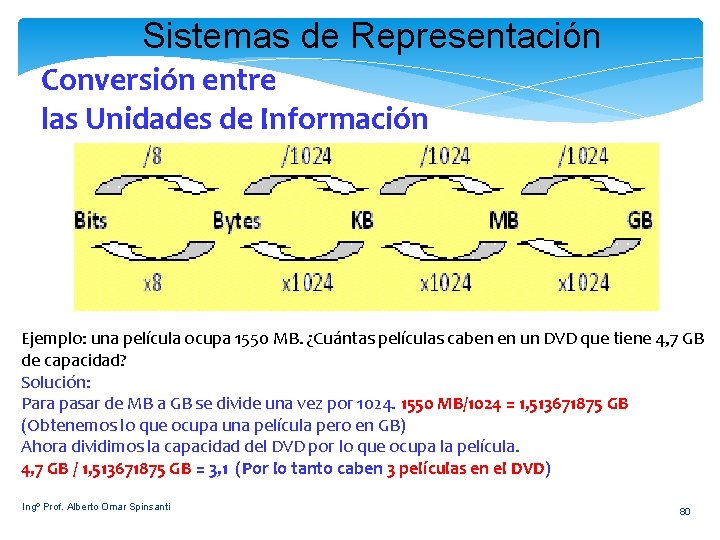
Sistemas de Representación Conversión entre las Unidades de Información Ejemplo: una película ocupa 1550 MB. ¿Cuántas películas caben en un DVD que tiene 4, 7 GB de capacidad? Solución: Para pasar de MB a GB se divide una vez por 1024. 1550 MB/1024 = 1, 513671875 GB (Obtenemos lo que ocupa una película pero en GB) Ahora dividimos la capacidad del DVD por lo que ocupa la película. 4, 7 GB / 1, 513671875 GB = 3, 1 (Por lo tanto caben 3 películas en el DVD) Ingº Prof. Alberto Omar Spinsanti 80

Sistemas de Representación Mayor información …… Ø Sistemas enteros, Punto fijo y Punto flotante ü Apunte 1 de Cátedra Ø Capítulo 2, 3 y 4. ü Quiroga patricia 1 ra Ed. Ø Capítulo 8: Aritmética del computador (8. 1. , 8. 2. , 8. 3. , 8. 4. , 8. 5. ) ü Stallings, 5 ta Ed. Ø Apéndice 8 A: Sistemas de Numeración ü Stallings, 5 ta Ed. Ø Link de interés ü http: //babbage. cs. qc. edu/IEEE-754/ Ingº Prof. Alberto Omar Spinsanti 81