Area of a Plane Region We know how






















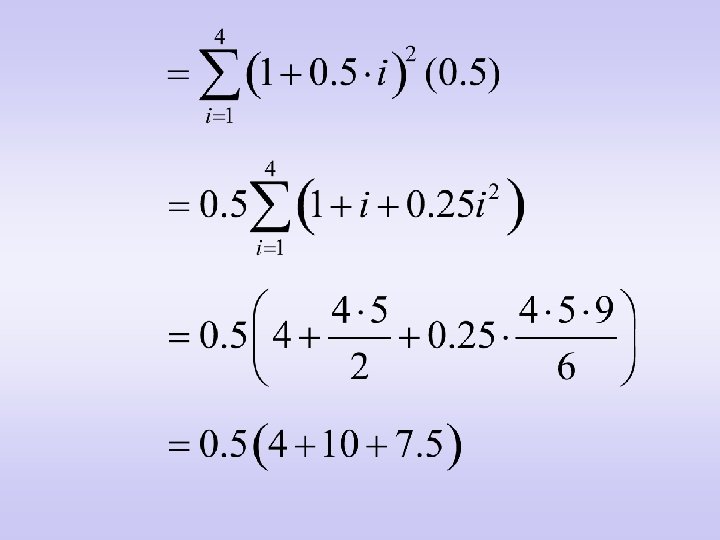





- Slides: 51

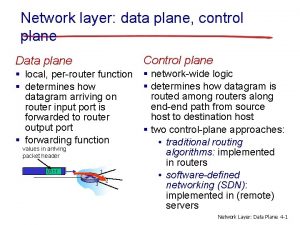
Area of a Plane Region • We know how to find the area inside many geometric shapes, like rectangles and triangles. • We will now consider finding the area under a curve. • The following example will be instructive in developing a general procedure.

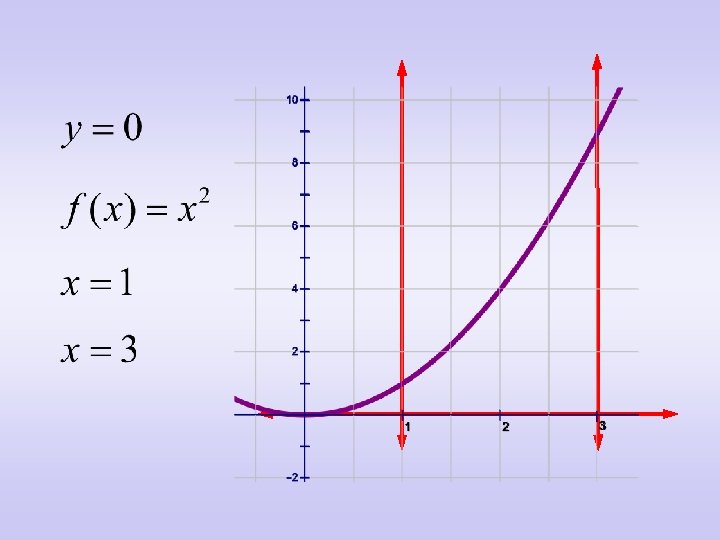
Area of a Plane Region • Find the approximate area of the region bounded by the graphs of:



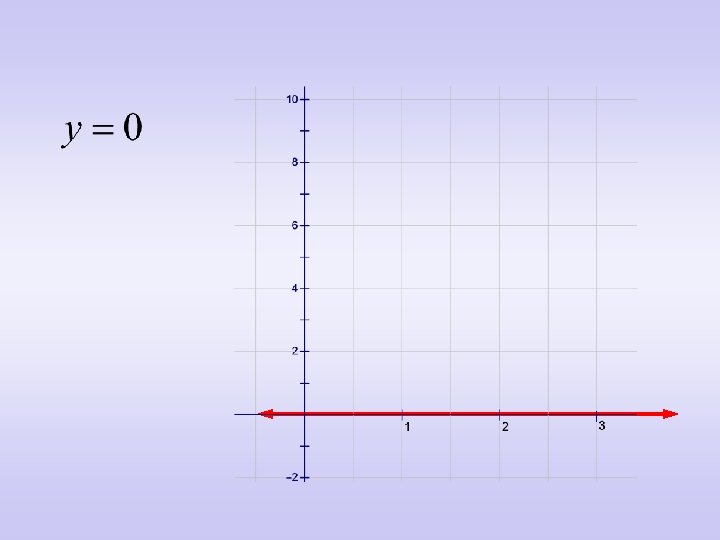
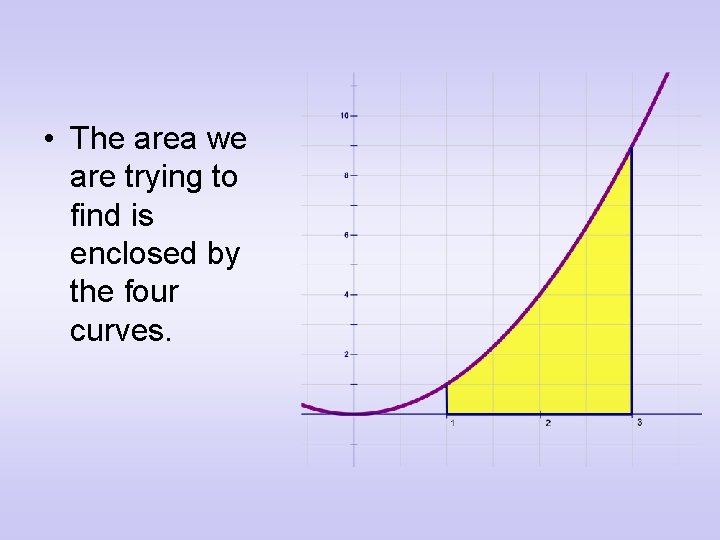
• The area we are trying to find is enclosed by the four curves.

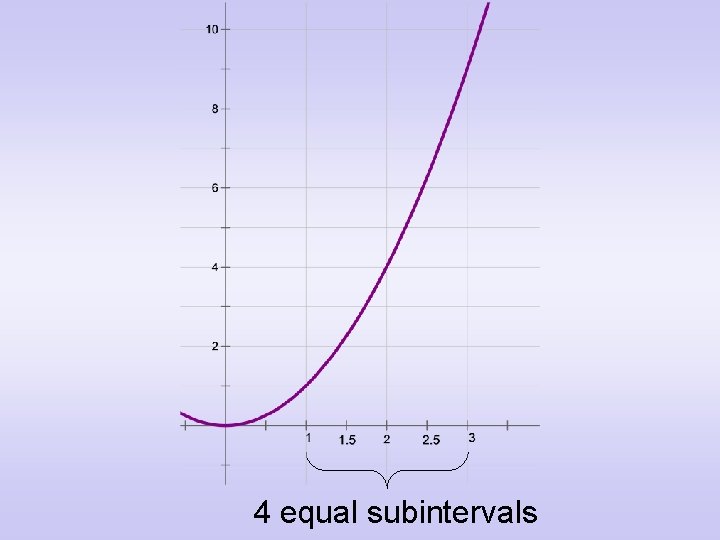
• We begin by dividing the interval from x = 1 to x = 3 into 4 equal subintervals. • Each of these subintervals are 0. 5 units wide.

• In general, if there are n equal subintervals from x = a to x = b, the width of each will be

• In general, where i is the ith subinterval, the left endpoint of each interval can be determined by:

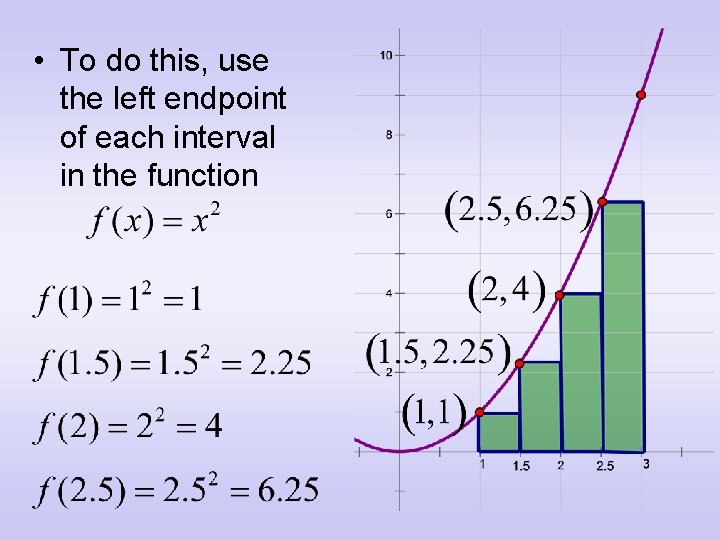
• Using the formula in the current example, the left end points are:

4 equal subintervals

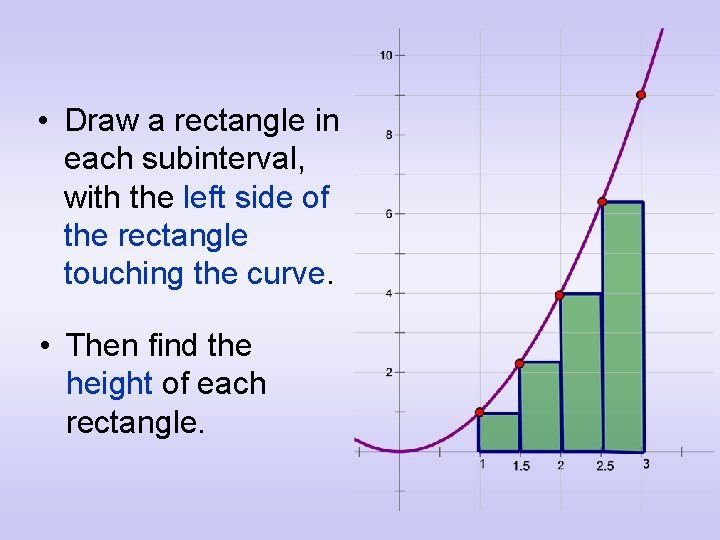
• Draw a rectangle in each subinterval, with the left side of the rectangle touching the curve. • Then find the height of each rectangle.

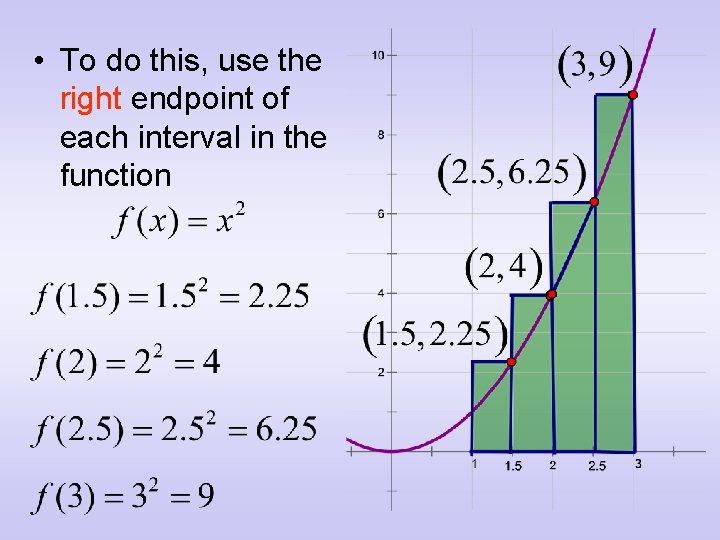
• To do this, use the left endpoint of each interval in the function

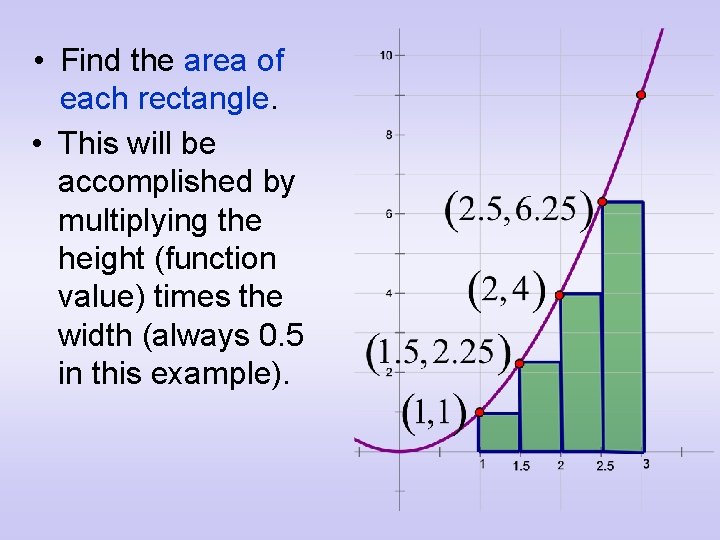
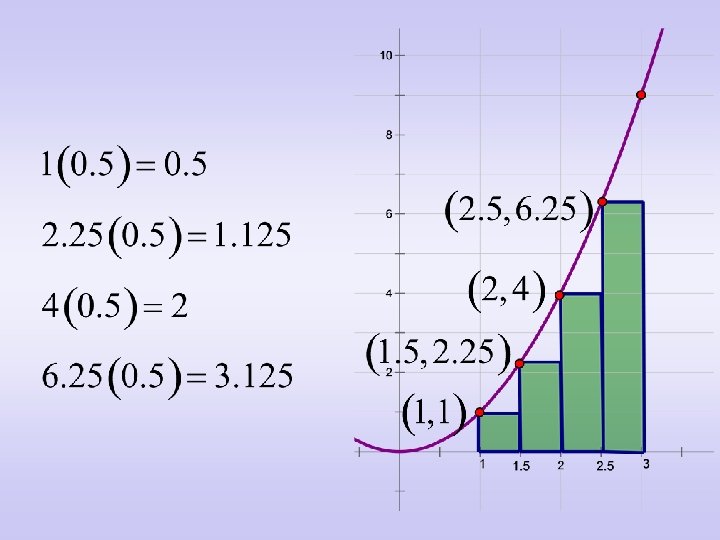
• Find the area of each rectangle. • This will be accomplished by multiplying the height (function value) times the width (always 0. 5 in this example).


• In general, to find the area of the ith rectangle with left endpoints, use the following:

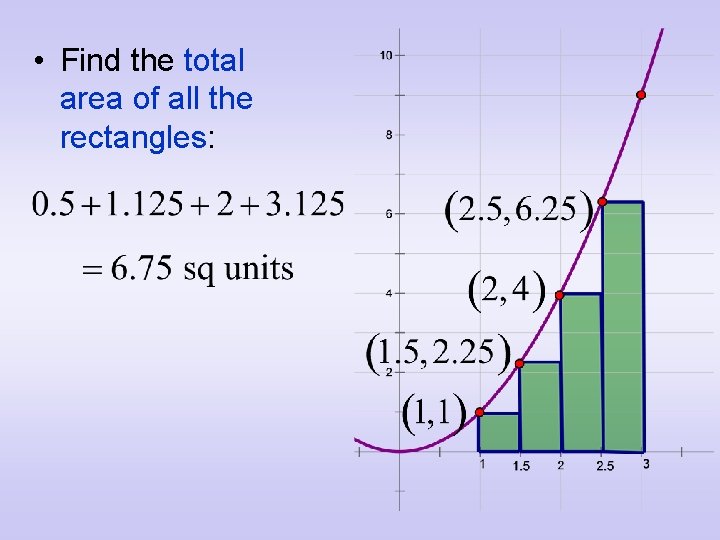
• Find the total area of all the rectangles:

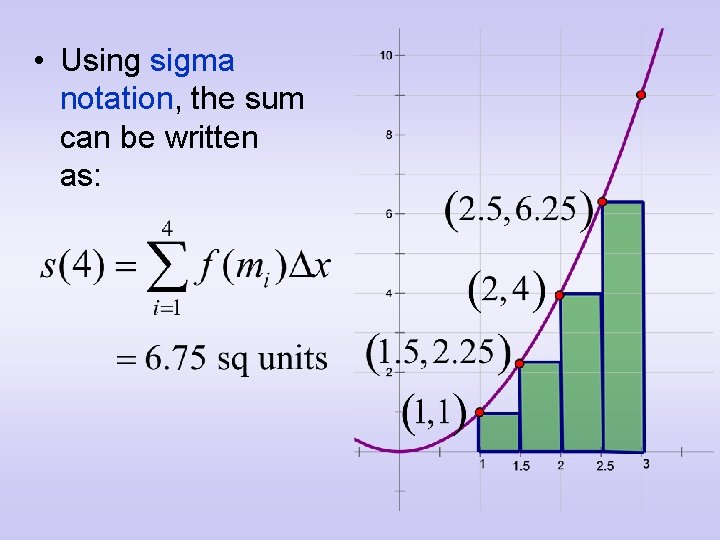
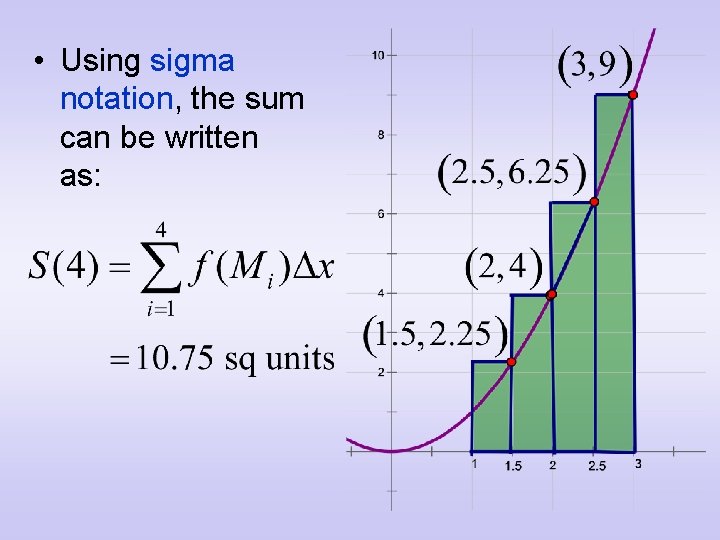
• Using sigma notation, the sum can be written as:

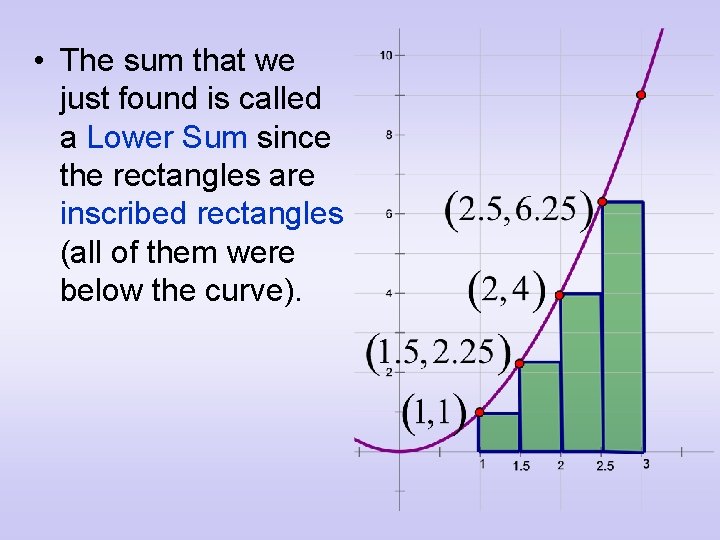
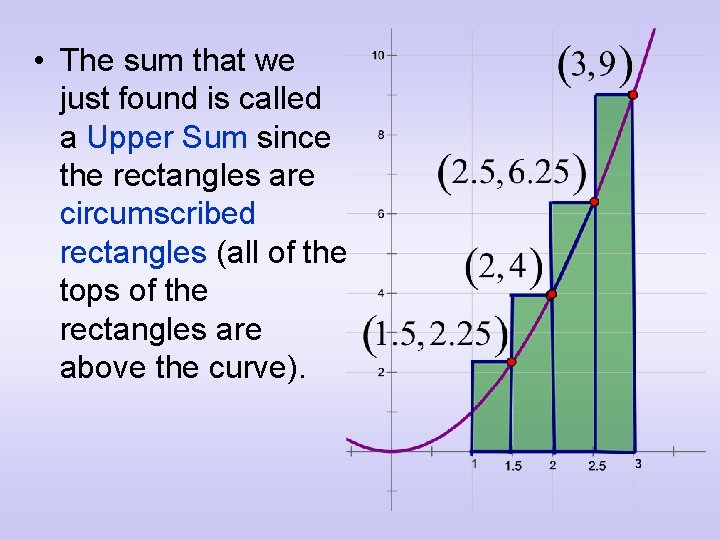
• The sum that we just found is called a Lower Sum since the rectangles are inscribed rectangles (all of them were below the curve).

• In general, to find the sum of the areas of all the rectangles using left endpoints, use the following:

Summary • Width of Intervals:

Summary • Left endpoint of the ith subinterval:

Summary • Area of the ith rectangle using left endpoints:

Summary • Total area of inscribed rectangles using left endpoints:

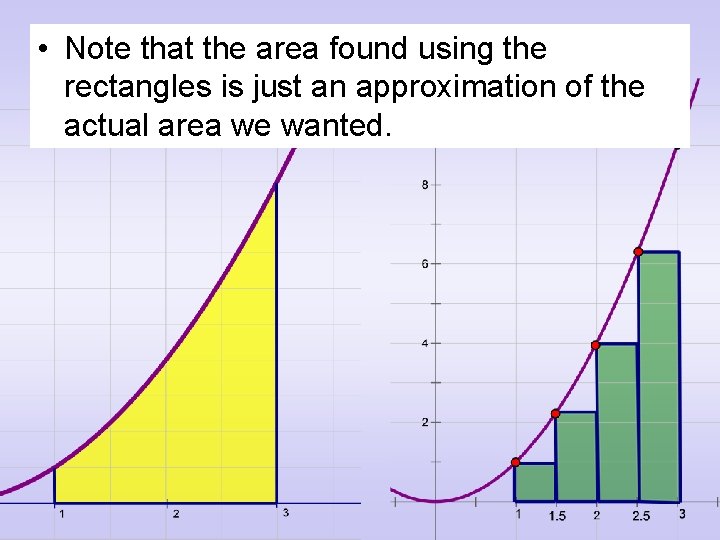
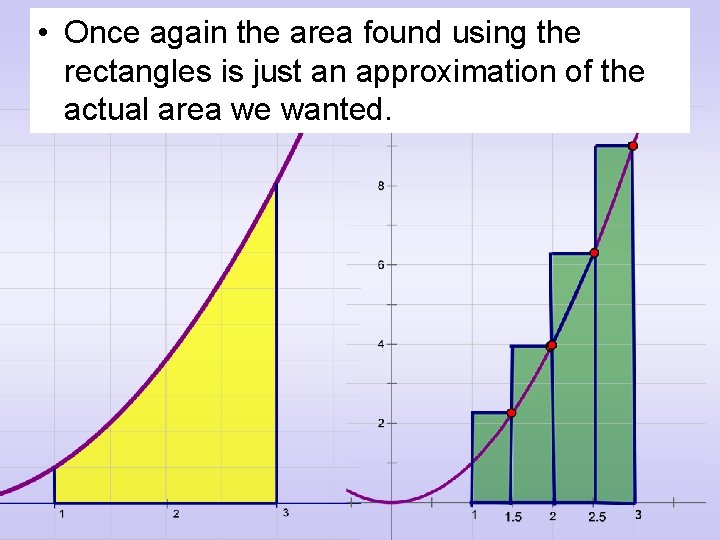
• Note that the area found using the rectangles is just an approximation of the actual area we wanted.

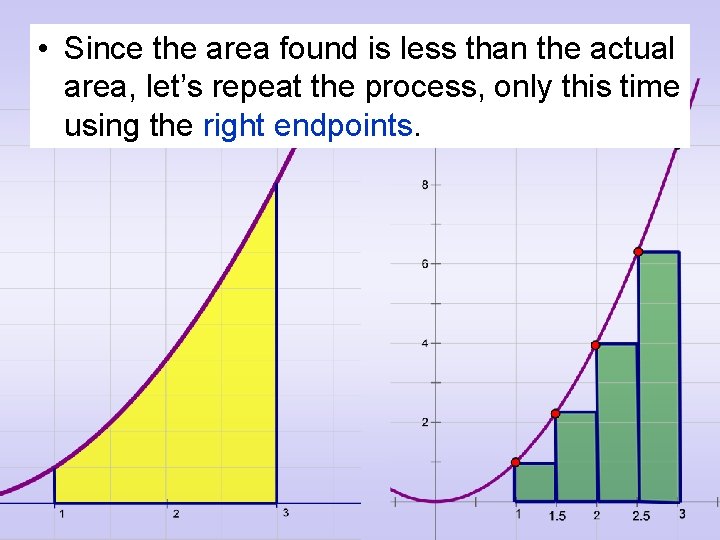
• Since the area found is less than the actual area, let’s repeat the process, only this time using the right endpoints.

• The width of each subinterval will be the same as before: • Each of the subintervals are 0. 5 units wide.

• In general, where i is the ith subinterval, the right endpoint of each interval can be determined by:

• Using the formula in the current example, the right end points are:

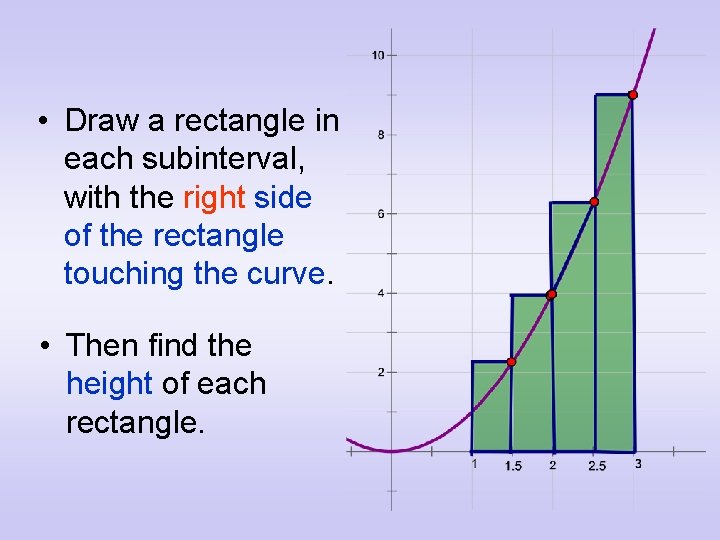
• Draw a rectangle in each subinterval, with the right side of the rectangle touching the curve. • Then find the height of each rectangle.

• To do this, use the right endpoint of each interval in the function

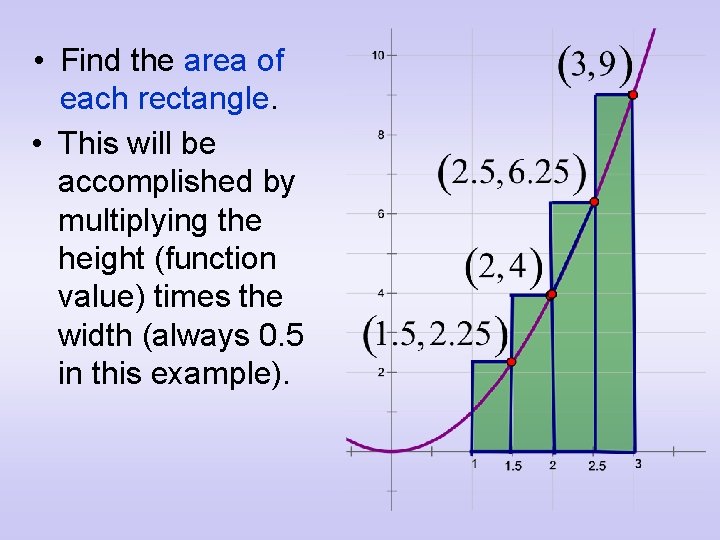
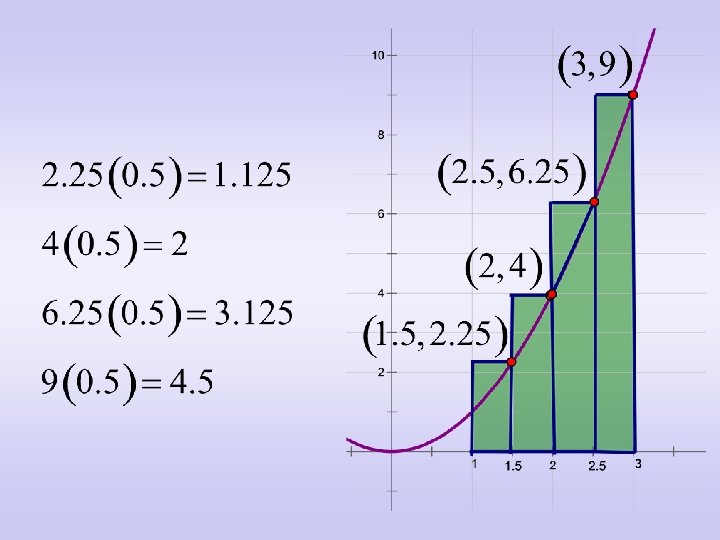
• Find the area of each rectangle. • This will be accomplished by multiplying the height (function value) times the width (always 0. 5 in this example).


• In general, to find the area of the ith rectangle with right endpoints, use the following:

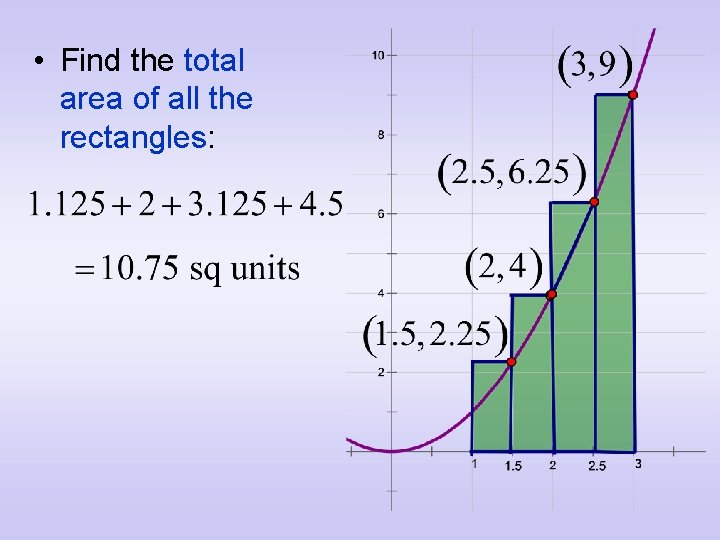
• Find the total area of all the rectangles:

• Using sigma notation, the sum can be written as:

• The sum that we just found is called a Upper Sum since the rectangles are circumscribed rectangles (all of the tops of the rectangles are above the curve).

• In general, to find the sum of the areas of all the rectangles using right endpoints, use the following:

Summary • Width of Intervals:

Summary • Right endpoint of the ith subinterval:

Summary • Area of the ith rectangle using right endpoints:

Summary • Total area of circumscribed rectangles using right endpoints:

• Rather than calculating the area of each rectangle and finding the sum, we can use the formulas.
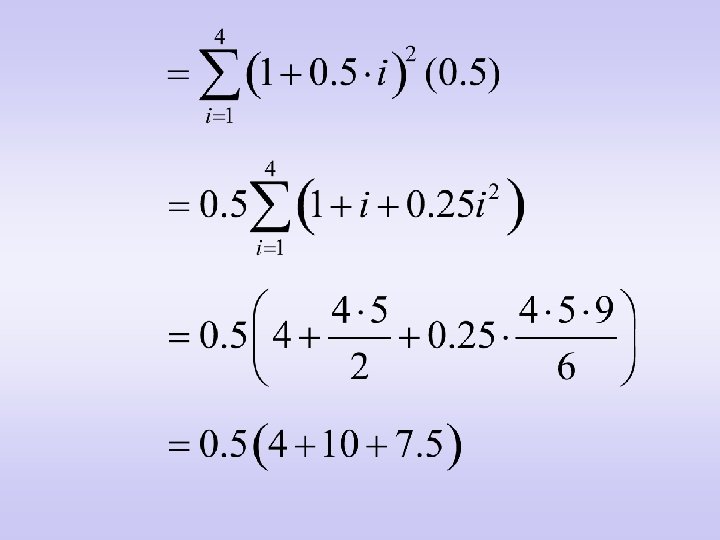

• Note that this is the same value found earlier in calculating the sum of the areas of the circumscribed rectangles.

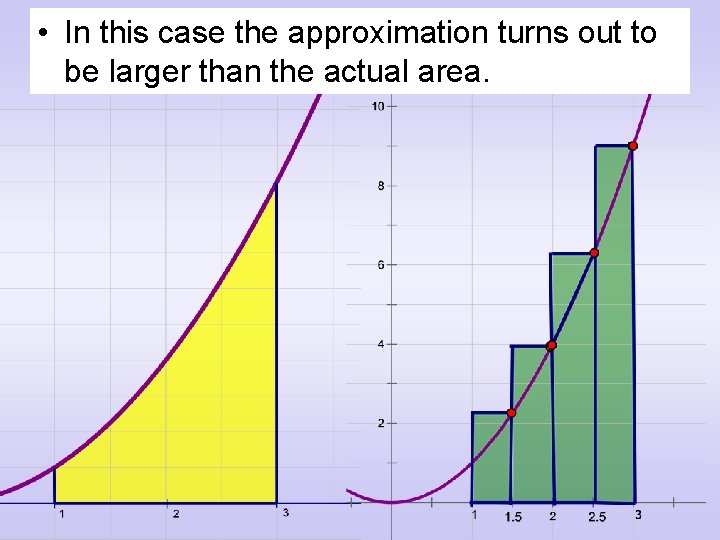
• Once again the area found using the rectangles is just an approximation of the actual area we wanted.

• In this case the approximation turns out to be larger than the actual area.

Area • Left Endpoints • Right Endpoints

Conclusion • We know the actual area is between 6. 75 sq units and 10. 75 sq units. This isn’t very “close”. How do we get a better estimate? • There are two possibilities: 1. Use rectangles that are closer to estimating the area. In the current example, using the midpoint of the interval would give a better estimate. 2. Use more rectangles. It can be shown that as the number of rectangles approaches infinity, the area will be exact.

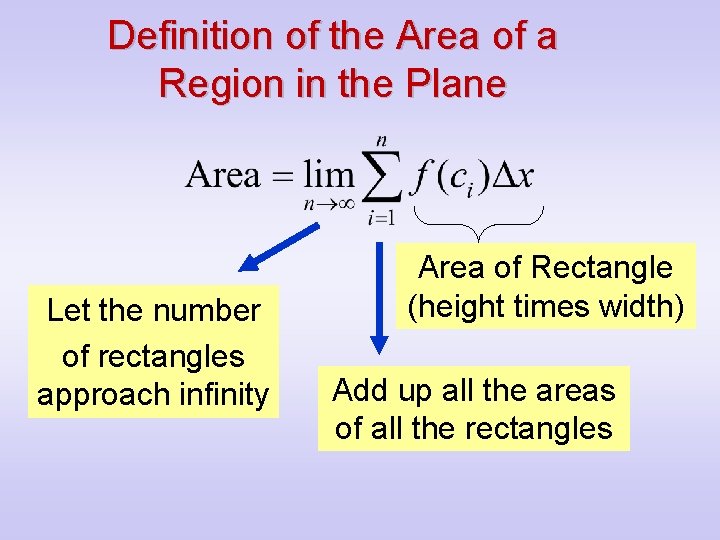
Definition of the Area of a Region in the Plane • Let function f be continuous and nonnegative on the interval [a, b] • The area of the region bounded by the graph of f, the x-axis, and the vertical lines x = a and x = b is given by:

Definition of the Area of a Region in the Plane • This is stating that ci can be any point in the interval, including the left or right endpoints. • This is the width of each interval.

Definition of the Area of a Region in the Plane Let the number of rectangles approach infinity Area of Rectangle (height times width) Add up all the areas of all the rectangles
 Software-defined networking: a comprehensive survey
Software-defined networking: a comprehensive survey Area of plane region
Area of plane region Know history know self
Know history know self Normalizing flow
Normalizing flow I know who goes before me
I know who goes before me Forward equivalence class
Forward equivalence class Inverse z-transform solved examples
Inverse z-transform solved examples 탄성계수
탄성계수 Subscapularis insertion and origin
Subscapularis insertion and origin Ece
Ece Perimeter and area in the coordinate plane
Perimeter and area in the coordinate plane Area of a figure
Area of a figure Waterplane coefficient formula
Waterplane coefficient formula Locate the centroid of the plane area shown.
Locate the centroid of the plane area shown. Areal fraction
Areal fraction 9-4 perimeter and area in the coordinate plane
9-4 perimeter and area in the coordinate plane 10-4 perimeter and area in the coordinate plane
10-4 perimeter and area in the coordinate plane What is ph in surface area
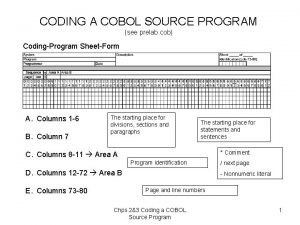
What is ph in surface area Cobol area a and area b
Cobol area a and area b Cobol area a and area b
Cobol area a and area b Curved surface area and total surface area of cone
Curved surface area and total surface area of cone What is the lateral area
What is the lateral area Cobol area a and area b
Cobol area a and area b Gatrulation
Gatrulation Area radicularis
Area radicularis Surface area vs area
Surface area vs area Maxillary denture landmarks
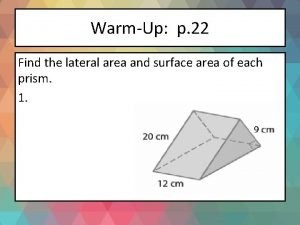
Maxillary denture landmarks Find the lateral area and surface area of each prism
Find the lateral area and surface area of each prism Lateral surface area
Lateral surface area Area radicularis
Area radicularis Area nervina area radicularis
Area nervina area radicularis Surface area vs lateral area
Surface area vs lateral area Lateral surface area of a prism
Lateral surface area of a prism Xxxxx 6
Xxxxx 6 What they don't know wont hurt them
What they don't know wont hurt them Disadvantages of sports
Disadvantages of sports What should every efl teacher know pdf
What should every efl teacher know pdf What do you know about africa
What do you know about africa Onion root tip mitosis stages
Onion root tip mitosis stages Those winter sundays by robert hayden theme
Those winter sundays by robert hayden theme 3 sides of health triangle
3 sides of health triangle Amontillado is a type of?
Amontillado is a type of? That you may know him
That you may know him Good teapot vs bad teapot
Good teapot vs bad teapot Fcat reference sheet
Fcat reference sheet How to know if a quadratic equation has one solution
How to know if a quadratic equation has one solution How to know if the slope is negative or positive
How to know if the slope is negative or positive Scentsy game
Scentsy game Scentsy how do you know the hostess
Scentsy how do you know the hostess Sabes bailar
Sabes bailar Christopher do you want to dance
Christopher do you want to dance Quadratic function
Quadratic function