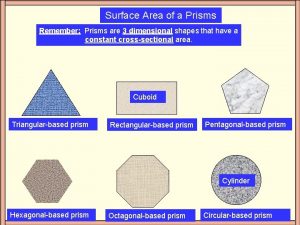
Find lateral areas and surface areas of prisms















- Slides: 21

• Find lateral areas and surface areas of prisms. • Find lateral areas and surface areas of cylinders.

Content Standards G. MG. 3 Apply geometric methods to solve problems (e. g. , designing an object or structure to satisfy physical constraints or minimize cost; working with typographic grid systems based on ratios). Mathematical Practices 1 Make sense of problems and persevere in solving them. 6 Attend to precision.

• lateral face • lateral edge • base edge • altitude • height • lateral area • axis • composite solid



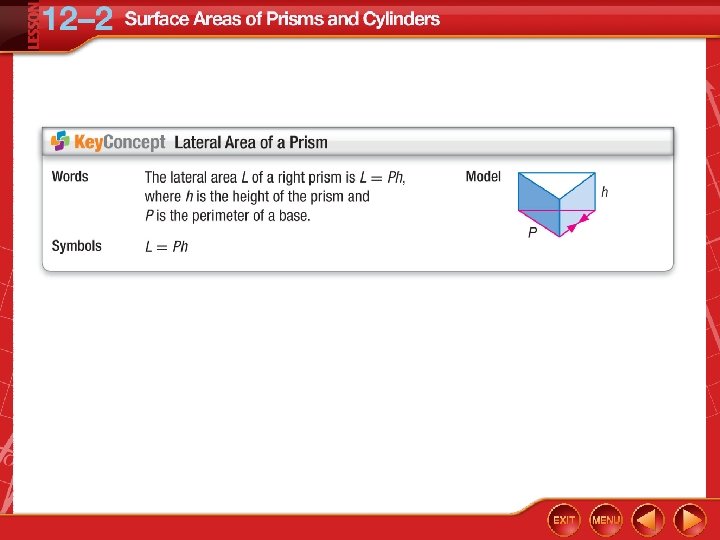
Lateral Area of a Prism Find the lateral area of the regular hexagonal prism. The bases are regular hexagons. So the perimeter of one base is 6(5) or 30 centimeters. Lateral area of a prism P = 30, h = 12 Multiply. Answer: The lateral area is 360 square centimeters.

Find the lateral area of the regular octagonal prism. A. 162 cm 2 B. 216 cm 2 C. 324 cm 2 D. 432 cm 2


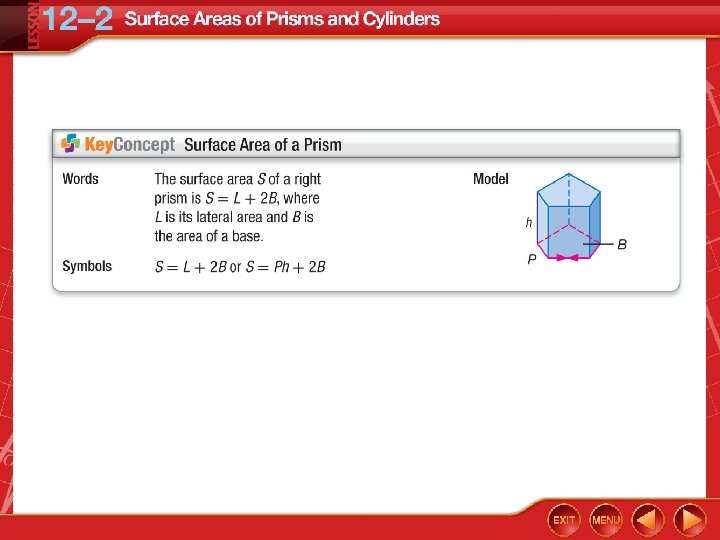
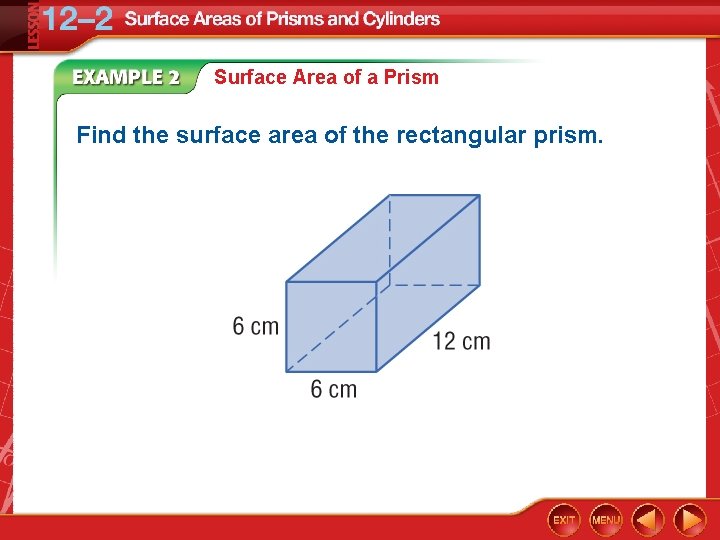
Surface Area of a Prism Find the surface area of the rectangular prism.

Surface Area of a Prism Surface area of a prism L = Ph Substitution Simplify. Answer: The surface area is 360 square centimeters.

Find the surface area of the triangular prism. A. 320 units 2 B. 512 units 2 C. 368 units 2 D. 416 units 2

Homework Page 850 (9 -16)



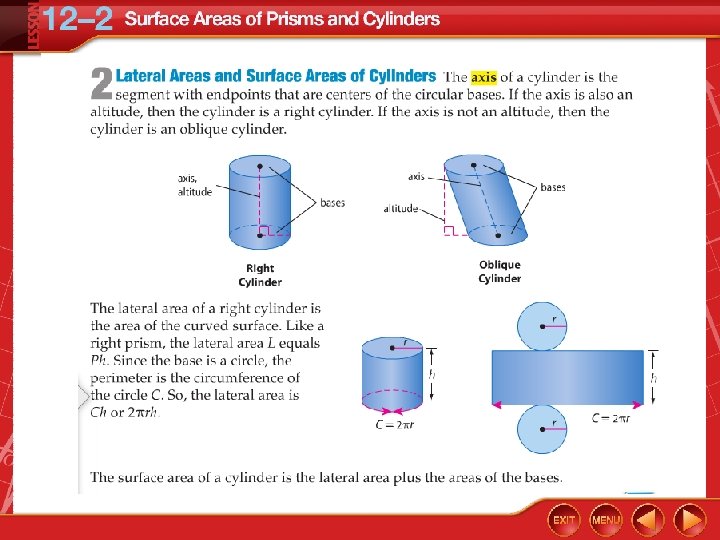
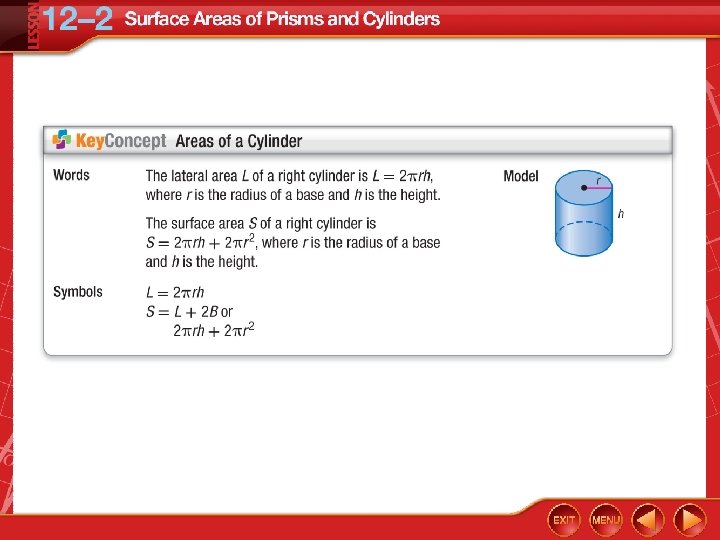
Lateral Area and Surface Area of a Cylinder Find the lateral area and the surface area of the cylinder. Round to the nearest tenth. L = 2 rh Lateral area of a cylinder = 2 (14)(18) Replace r with 14 and h with 18. ≈ 1583. 4 Use a calculator.

Lateral Area and Surface Area of a Cylinder S = 2 rh + 2 r 2 Surface area of a cylinder ≈ 1583. 4 + 2 (14)2 Replace 2 rh with 1583. 4 and r with 14. ≈ 2814. 9 Use a calculator. Answer: The lateral area is about 1583. 4 square feet and the surface area is about 2814. 9 square feet.

Find the lateral area and the surface area of the cylinder. Round to the nearest tenth. A. lateral area ≈ 1508 ft 2 and surface area ≈ 2412. 7 ft 2 B. lateral area ≈ 1508 ft 2 and surface area ≈ 1206. 4 ft 2 C. lateral area ≈ 754 ft 2 and surface area ≈ 2412. 7 ft 2 D. lateral area ≈ 754 ft 2 and surface area ≈ 1206. 4. 7 ft 2

Find Missing Dimensions MANUFACTURING A soup can is covered with the label shown. What is the radius of the soup can? L = 2 rh Lateral area of a cylinder 125. 6 = 2 r(8) Replace L with 15. 7 ● 8 and h with 8. 125. 6 = 16 r Simplify. 2. 5 ≈ r Divide each side by 16.

Find Missing Dimensions Answer: The radius of the soup can is about 2. 5 inches.

Find the diameter of a base of a cylinder if the surface area is 480 square inches and the height is 8 inches. A. 12 inches B. 16 inches C. 18 inches D. 24 inches

Homework Page 850 (19 -22, 25)
 11-2 surface areas of prisms and cylinders
11-2 surface areas of prisms and cylinders Lesson 12-2 surface areas of prisms and cylinders
Lesson 12-2 surface areas of prisms and cylinders Surface area of prisms and cylinders homework answers
Surface area of prisms and cylinders homework answers 11-2 surface areas of prisms and cylinders answers
11-2 surface areas of prisms and cylinders answers Surface area of prisms and cylinders homework answers
Surface area of prisms and cylinders homework answers How to find the lateral area of a regular octagonal prism
How to find the lateral area of a regular octagonal prism Rectangular prism unfolded
Rectangular prism unfolded Lateral surface area of a rectangular prism
Lateral surface area of a rectangular prism Lateral and surface area
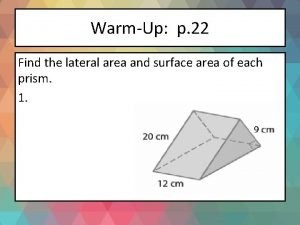
Lateral and surface area Find the lateral area and surface area of each prism
Find the lateral area and surface area of each prism Prism volume and surface area worksheet
Prism volume and surface area worksheet Surface area of prisms
Surface area of prisms Volume and surface area of prisms maze worksheet
Volume and surface area of prisms maze worksheet 13-2 surface area of prisms and pyramids
13-2 surface area of prisms and pyramids 10-4 surface area of prisms and cylinders
10-4 surface area of prisms and cylinders Lesson 10-4 surface area of prisms and cylinders
Lesson 10-4 surface area of prisms and cylinders Volumes of prisms and cylinders worksheet
Volumes of prisms and cylinders worksheet Volume of cylinders cones and spheres vocabulary
Volume of cylinders cones and spheres vocabulary Cuboid formula
Cuboid formula Surface area prism
Surface area prism What is the area of the base
What is the area of the base Csa of cone
Csa of cone