Surface Areas and Volumes of Prisms and Cylinders

Surface Areas and Volumes of Prisms and Cylinders

The net of a right prism can be drawn so that the lateral faces form a rectangle with the same height as the prism. The base of the rectangle is equal to the perimeter of the base of the prism. LA = 2(hw) + 2(lh) SA = 2(lw) + 2(hw) + 2(lh)

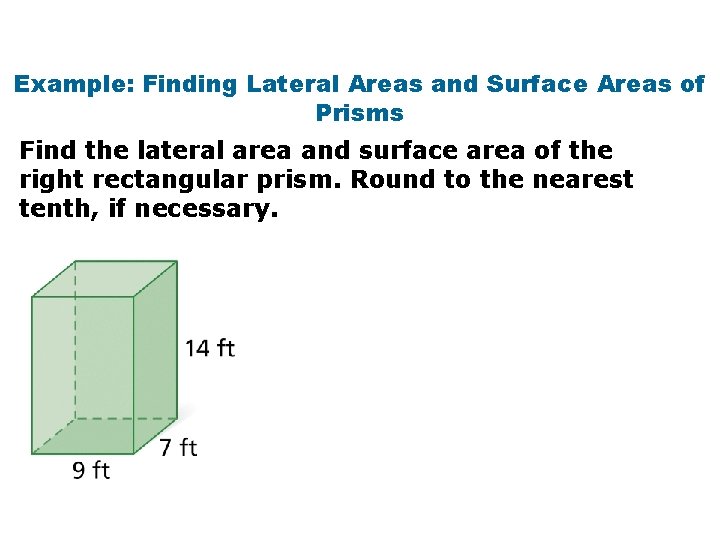
Example: Finding Lateral Areas and Surface Areas of Prisms Find the lateral area and surface area of the right rectangular prism. Round to the nearest tenth, if necessary.

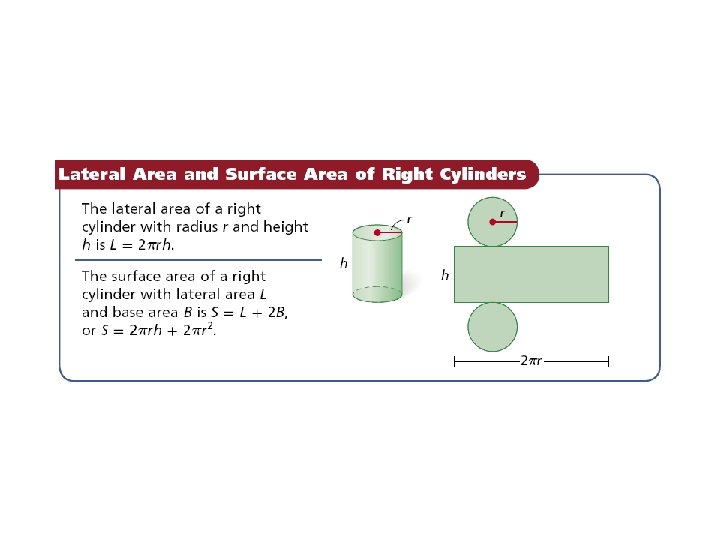
Example: Finding Lateral Areas and Surface Areas of Right Cylinders Find the lateral area and surface area of the right cylinder. Give your answers in terms of .

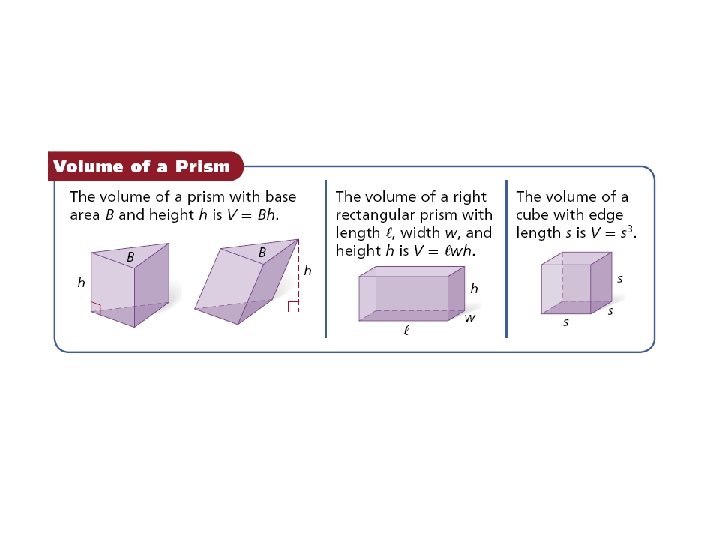
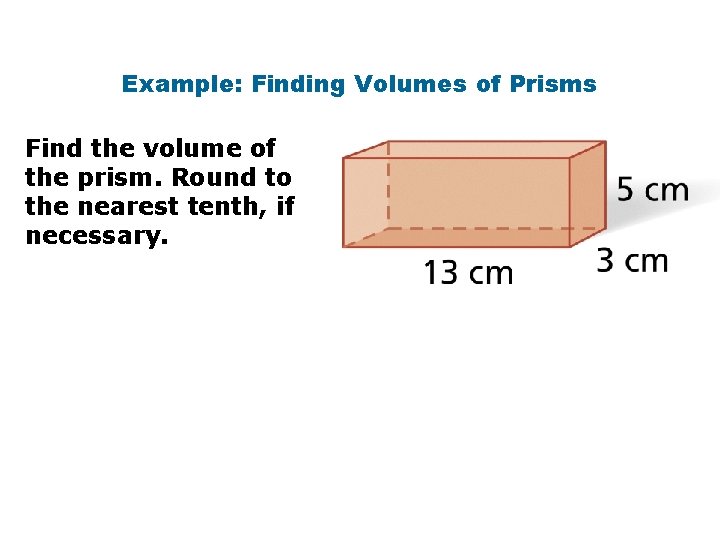
Example: Finding Volumes of Prisms Find the volume of the prism. Round to the nearest tenth, if necessary.

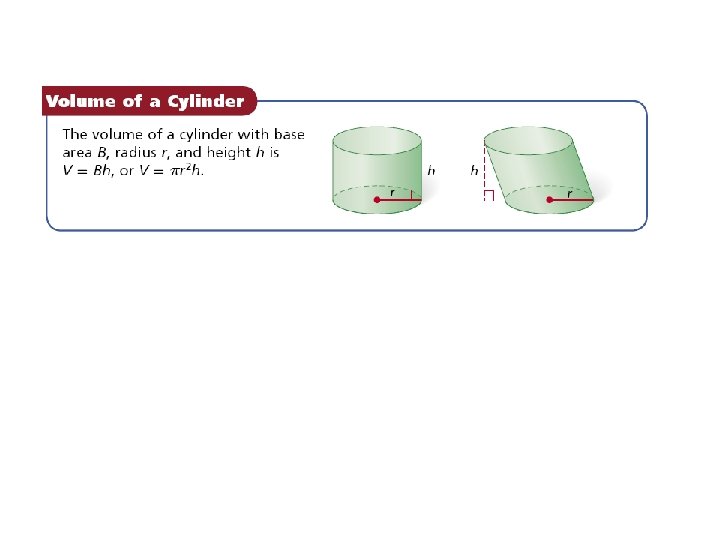
Example: Finding Volumes of Cylinders Find the volume of the cylinder. Give your answers in terms of and rounded to the nearest tenth.

Lesson Quiz: Part I Find the surface area of each figure. Round to the nearest tenth, if necessary. 1. a right rectangular prism with length 14 cm, width 11 cm, and height 18 cm SA = 1208 cm 2 2. a cube with edge length 22 ft SA = 2904 ft 2 3. a cylinder with diameter 16 in. and height 7 in. SA 753. 98 in 2

Lesson Quiz: Part I Find the volume of each figure. Round to the nearest tenth, if necessary. 1. a right rectangular prism with length 14 cm, width 11 cm, and height 18 cm V = 2772 cm 3 2. a cube with edge length 22 ft V = 10, 648 ft 3 3. a cylinder with diameter 16 in. and height 7 in. V 1407. 4 in 3