10 4 Surface Area of Prisms and Cylinders

10 -4 Surface Area of Prisms and Cylinders Warm Up Find the perimeter and area of each polygon. 1. a rectangle with base 14 cm and height 9 cm P = 46 cm; A = 126 cm 2 Holt Geometry

10 -4 Surface Area of Prisms and Cylinders Holt Geometry

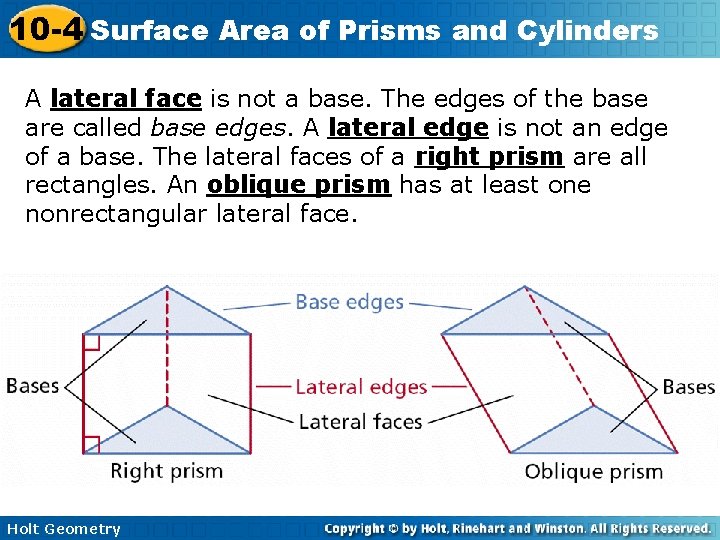
10 -4 Surface Area of Prisms and Cylinders A lateral face is not a base. The edges of the base are called base edges. A lateral edge is not an edge of a base. The lateral faces of a right prism are all rectangles. An oblique prism has at least one nonrectangular lateral face. Holt Geometry

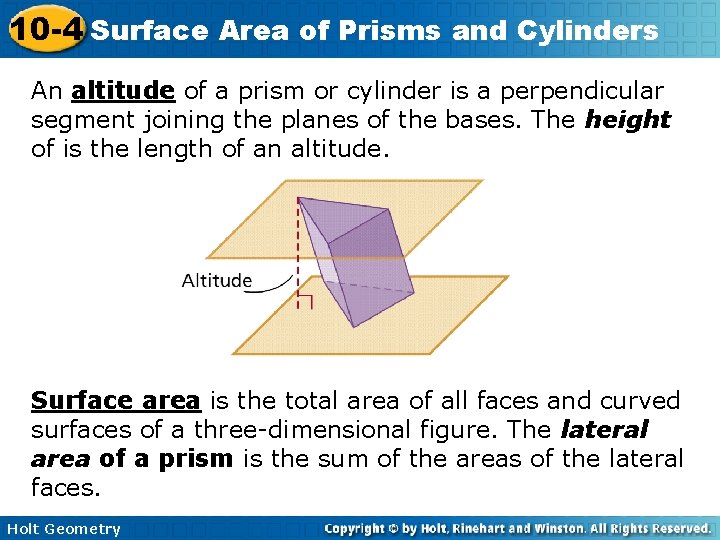
10 -4 Surface Area of Prisms and Cylinders An altitude of a prism or cylinder is a perpendicular segment joining the planes of the bases. The height of is the length of an altitude. Surface area is the total area of all faces and curved surfaces of a three-dimensional figure. The lateral area of a prism is the sum of the areas of the lateral faces. Holt Geometry

10 -4 Surface Area of Prisms and Cylinders The surface area of a right rectangular prism S = 2ℓw + 2 wh + 2ℓh. Holt Geometry

10 -4 Surface Area of Prisms and Cylinders Example 1 A: Finding Lateral Areas and Surface Areas of Prisms Find the lateral area and surface area of the right rectangular prism. Round to the nearest tenth, if necessary. L = Ph P = 2(9) + 2(7) = 32 ft = 32(14) = 448 ft 2 S = Ph + 2 B = 448 + 2(7)(9) = 574 ft 2 Holt Geometry

10 -4 Surface Area of Prisms and Cylinders Check It Out! Example 1 Find the lateral area and surface area of a cube with edge length 8 cm. L = Ph = 32(8) = 256 cm 2 P = 4(8) = 32 cm S = Ph + 2 B = 256 + 2(8)(8) = 384 cm 2 Holt Geometry

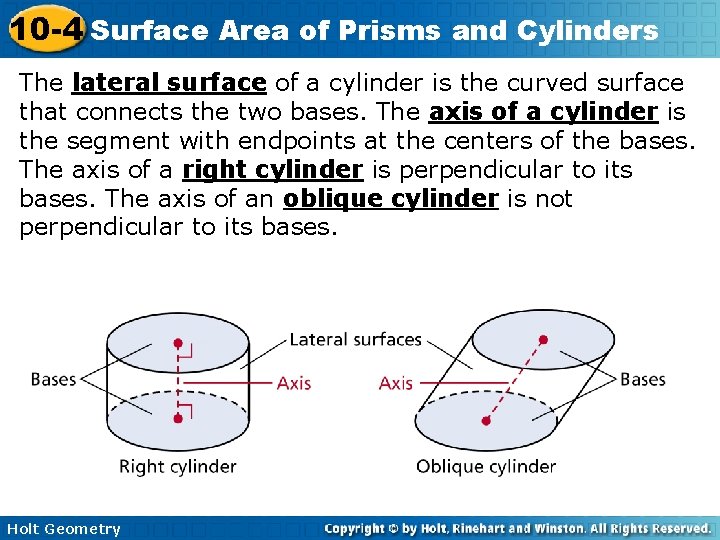
10 -4 Surface Area of Prisms and Cylinders The lateral surface of a cylinder is the curved surface that connects the two bases. The axis of a cylinder is the segment with endpoints at the centers of the bases. The axis of a right cylinder is perpendicular to its bases. The axis of an oblique cylinder is not perpendicular to its bases. Holt Geometry

10 -4 Surface Area of Prisms and Cylinders Holt Geometry

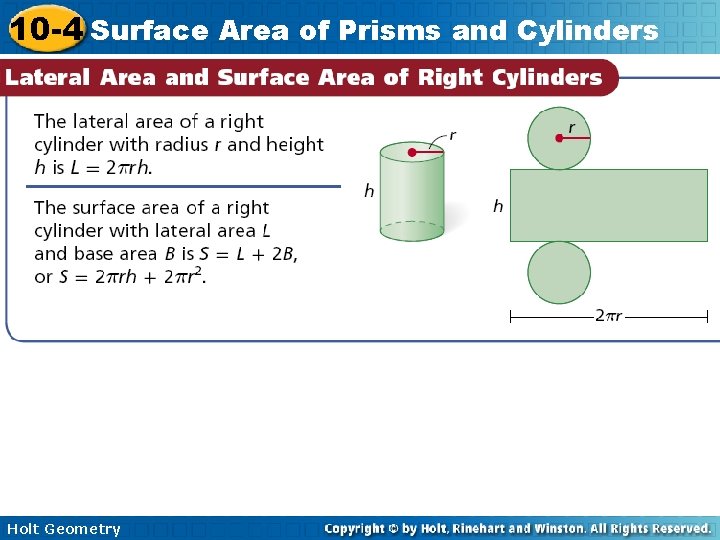
10 -4 Surface Area of Prisms and Cylinders Example 2 A: Finding Lateral Areas and Surface Areas of Right Cylinders Find the lateral area and surface area of the right cylinder. Give your answers in terms of . The radius is half the diameter, or 8 ft. L = 2 rh = 2 (8)(10) = 160 in 2 S = L + 2 r 2 = 160 + 2 (8)2 = 288 in 2 Holt Geometry

10 -4 Surface Area of Prisms and Cylinders Example 2 B: Finding Lateral Areas and Surface Areas of Right Cylinders Find the lateral area and surface area of a right cylinder with circumference 24 cm and a height equal to half the radius. Give your answers in terms of . Step 1 Use the circumference to find the radius. C = 2 r 24 = 2 r r = 12 Holt Geometry Circumference of a circle Substitute 24 for C. Divide both sides by 2.

10 -4 Surface Area of Prisms and Cylinders Example 2 B Continued Find the lateral area and surface area of a right cylinder with circumference 24 cm and a height equal to half the radius. Give your answers in terms of . Step 2 Use the radius to find the lateral area and surface area. The height is half the radius, or 6 cm. L = 2 rh = 2 (12)(6) = 144 cm 2 Lateral area S = L + 2 r 2 = 144 + 2 (12)2 Surface area = 432 in 2 Holt Geometry

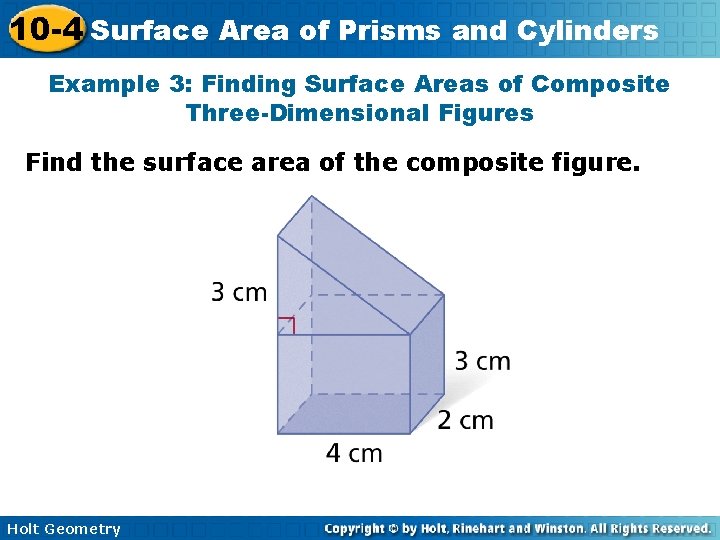
10 -4 Surface Area of Prisms and Cylinders Example 3: Finding Surface Areas of Composite Three-Dimensional Figures Find the surface area of the composite figure. Holt Geometry

10 -4 Surface Area of Prisms and Cylinders The surface area of the rectangular prism is A right triangular prism is added to the rectangular prism. . The surface area of the triangular prism is Two copies of the rectangular prism base are removed. The area of the base is B = 2(4) = 8 cm 2. . S = (rectangular prism surface area) + (triangular prism surface area) – 2(rectangular prism base area) S = 52 + 36 – 2(8) = 72 cm 2 Holt Geometry

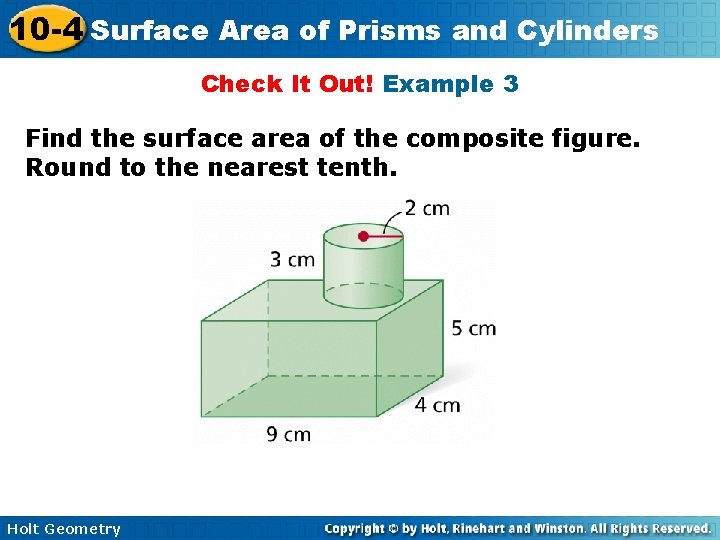
10 -4 Surface Area of Prisms and Cylinders Check It Out! Example 3 Find the surface area of the composite figure. Round to the nearest tenth. Holt Geometry

10 -4 Surface Area of Prisms and Cylinders Remember! Always round at the last step of the problem. Use the value of given by the key on your calculator. Holt Geometry

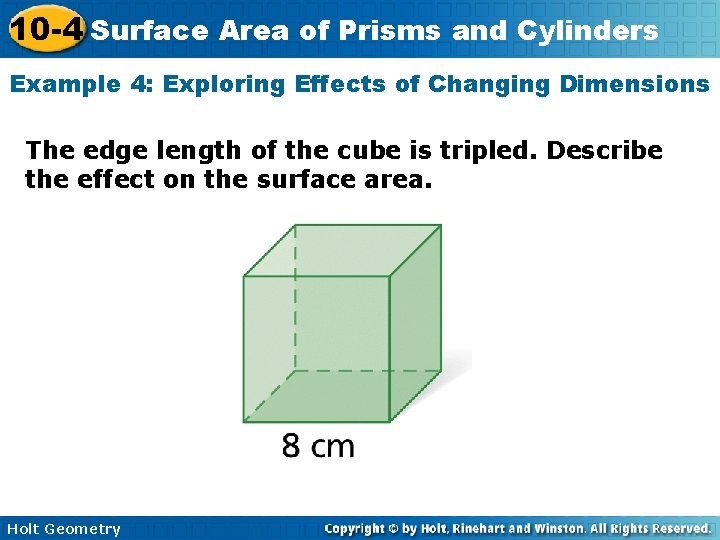
10 -4 Surface Area of Prisms and Cylinders Example 4: Exploring Effects of Changing Dimensions The edge length of the cube is tripled. Describe the effect on the surface area. Holt Geometry

10 -4 Surface Area of Prisms and Cylinders Example 4 Continued 24 cm original dimensions: edge length tripled: S = 6ℓ 2 = 6(8)2 = 384 cm 2 S = 6ℓ 2 = 6(24)2 = 3456 cm 2 Notice than 3456 = 9(384). If the length, width, and height are tripled, the surface area is multiplied by 32, or 9. Holt Geometry

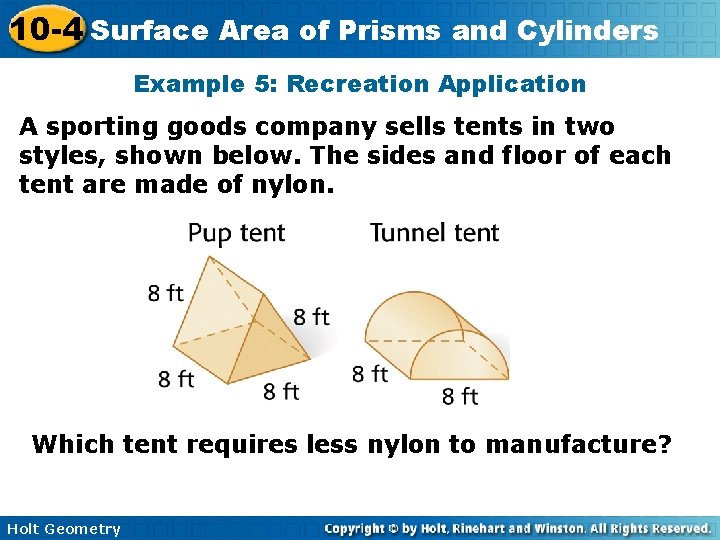
10 -4 Surface Area of Prisms and Cylinders Example 5: Recreation Application A sporting goods company sells tents in two styles, shown below. The sides and floor of each tent are made of nylon. Which tent requires less nylon to manufacture? Holt Geometry

10 -4 Surface Area of Prisms and Cylinders Example 5 Continued Pup tent: Tunnel tent: The tunnel tent requires less nylon. Holt Geometry

10 -4 Surface Area of Prisms and Cylinders Lesson Quiz: Part I Find the lateral area and the surface area of each figure. Round to the nearest tenth, if necessary. 1. a cube with edge length 10 cm L = 400 cm 2 ; S = 600 cm 2 2. a regular hexagonal prism with height 15 in. and base edge length 8 in. L = 720 in 2; S 1052. 6 in 2 3. a right cylinder with base area 144 cm 2 and a height that is the radius L 301. 6 cm 2; S = 1206. 4 cm 2 Holt Geometry

10 -4 Surface Area of Prisms and Cylinders Lesson Quiz: Part II 4. A cube has edge length 12 cm. If the edge length of the cube is doubled, what happens to the surface area? The surface area is multiplied by 4. 5. Find the surface area of the composite figure. S = 3752 m 2 Holt Geometry