LESSON Surface Areas of Prisms Cylinders 12 2

LESSON Surface Areas of Prisms & Cylinders 12 -2 Honors Geometry Warm- Up: Discovery Activity Today: • 12. 1 Questions • 12. 2 Discovery • 12. 2 Lesson

LESSON 12 -2 Surface Areas of Prisms & Cylinders 12. 2 Surface Area of Prisms and Cylinders Objective: 1. Find lateral areas and surface areas of prisms. 2. Find lateral areas and surface areas of cylinders. Vocabulary: lateral face, lateral edge, base edge, altitude, height, lateral area, axis, composite solid

LESSON 12 -2 Surface Areas of Prisms & Cylinders polyhedra – solids with flat polygon faces and the segments of intersection are called edges prism – a polyhedron with 2 parallel congruent faces and parallel edges that connect corresponding vertices – named by the base – 2 parallel and congruent faces lateral edges – parallel lines joining corresponding vertices of the bases lateral face – non-base sides

LESSON 12 -2 Surface Areas of Prisms & Cylinders right prism – a prism where the lateral edges are perpendicular to the bases (does not mean the bases have right angles) regular prism – a prism with bases that are regular lateral surface area (L) – the sum of the areas of the lateral faces total surface area (S)– the sum of the prism’s lateral area and the areas of the two bases

LESSON 12 -2 Surface Areas of Prisms & Cylinders The lateral area (L) of a right prism is the product of the height and the perimeter of the base. L = Ph P is the perimeter of the base and h is the height of the prism. The total area of a prism is the sum of the prism’s lateral area and the areas of the two bases. S = L + 2 B

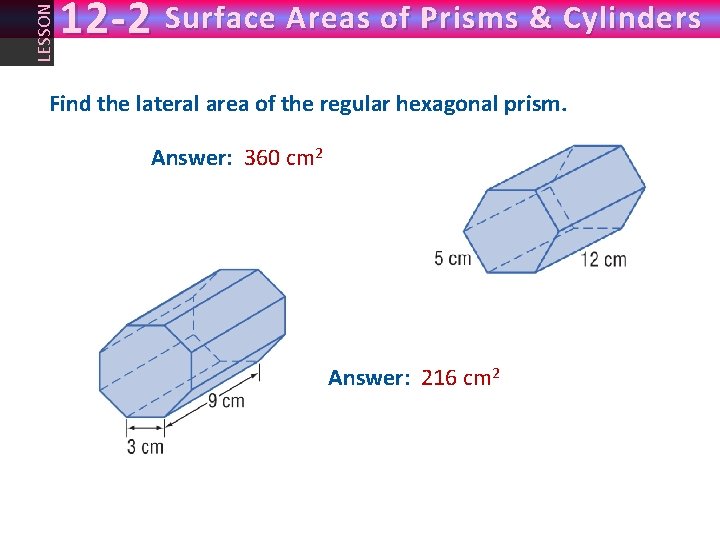
LESSON 12 -2 Surface Areas of Prisms & Cylinders Find the lateral area of the regular hexagonal prism. Answer: 360 cm 2 Answer: 216 cm 2

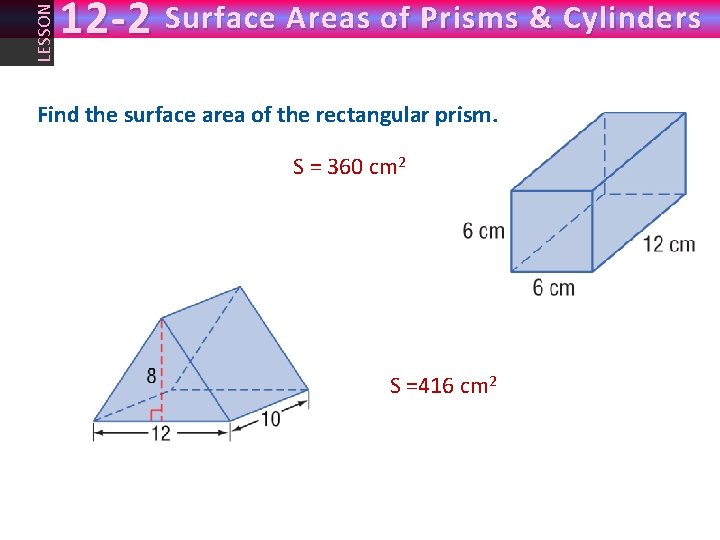
LESSON 12 -2 Surface Areas of Prisms & Cylinders Find the surface area of the rectangular prism. S = 360 cm 2 S =416 cm 2

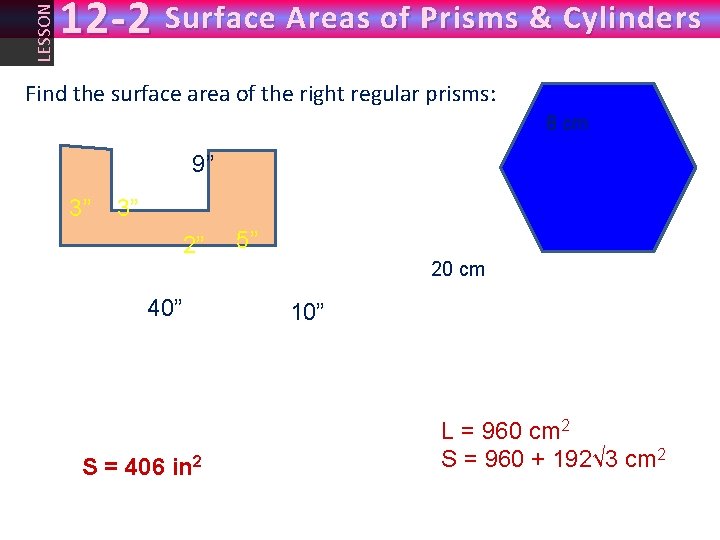
LESSON 12 -2 Surface Areas of Prisms & Cylinders Find the surface area of the right regular prisms: 8 cm 5” 3” 9” 3” 2” 40” S = 406 in 2 5” 20 cm 10” L = 960 cm 2 S = 960 + 192√ 3 cm 2

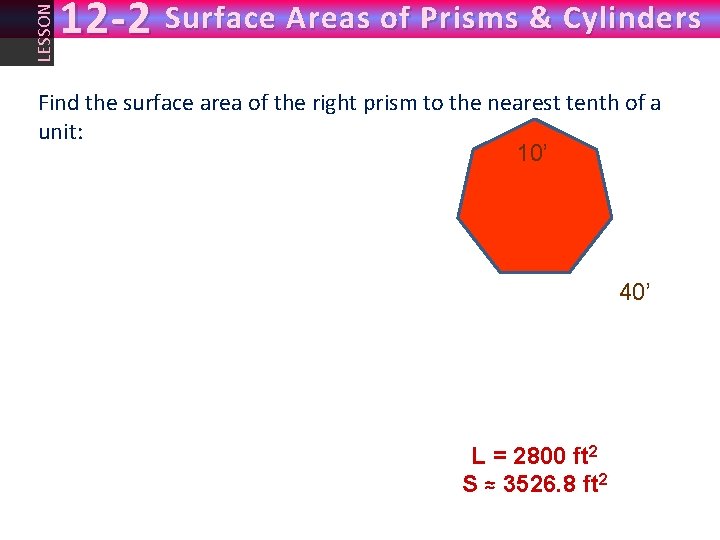
LESSON 12 -2 Surface Areas of Prisms & Cylinders Find the surface area of the right prism to the nearest tenth of a unit: 10’ 40’ L = 2800 ft 2 S ≈ 3526. 8 ft 2

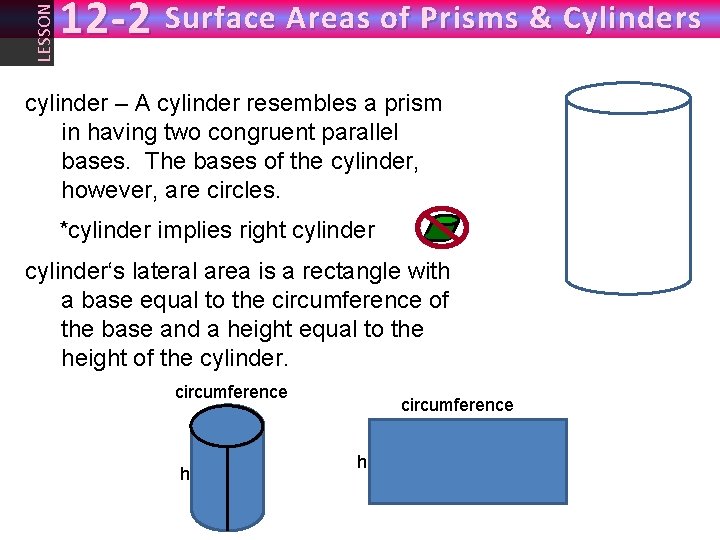
LESSON 12 -2 Surface Areas of Prisms & Cylinders cylinder – A cylinder resembles a prism in having two congruent parallel bases. The bases of the cylinder, however, are circles. *cylinder implies right cylinder‘s lateral area is a rectangle with a base equal to the circumference of the base and a height equal to the height of the cylinder. circumference h

LESSON 12 -2 Surface Areas of Prisms & Cylinders The lateral area (L) of a cylinder is equal to the product of the height and the circumference of the base. Lcylinder = Ch = 2πrh C is the circumference, h is the height of the cylinder and r is the radius of the base. The total area of a cylinder is the sum of the cylinder’s lateral area and the areas of the two bases (circles). S = L + 2 B

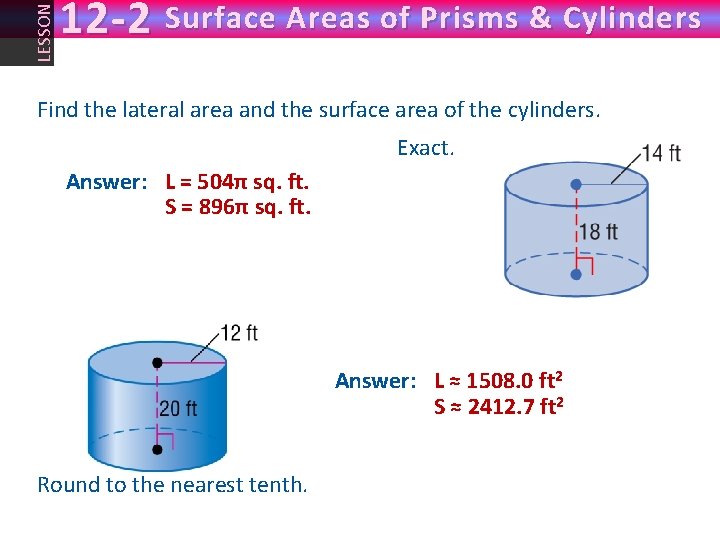
LESSON 12 -2 Surface Areas of Prisms & Cylinders Find the lateral area and the surface area of the cylinders. Exact. Answer: L = 504π sq. ft. ≈ 1583. 4 sq. ft. S = 896π sq. ft. ≈ 2814. 9 sq. ft. Answer: L ≈ 1508. 0 ft 2 S ≈ 2412. 7 ft 2 Round to the nearest tenth.

LESSON 12 -2 Surface Areas of Prisms & Cylinders MANUFACTURING A soup can is covered with the label shown. What is the radius of the soup can? 8 in. 15. 7 in. Answer: r ≈ 2. 5”

LESSON 12 -2 Surface Areas of Prisms & Cylinders Find the diameter of a base of a cylinder if the surface area is 480 square inches and the height is 8 inches. A. 12 inches B. 16 inches C. 18 inches D. 24 inches

LESSON 12 -2 Surface Areas of Prisms & Cylinders Find the surface area of the composite solids. 10’ 30’ 20” 30” 12” S = 2040 + 216π in 2 ≈ 2719 in 2 20’ S = 1050π ft 2 ≈ 3299 ft 2

LESSON 12 -2 Surface Areas of Prisms & Cylinders Assignment Due tomorrow: • 12. 2 P. 850 #9 -33 odd, 43 – you must show work including formulas!