Surface Area of Prisms Cylinders Objectives 1 To

Surface Area of Prisms & Cylinders Objectives: 1) To find the surface area of a prism. 2) To find the surface area of a cylinder.

I. Surface Area of a Prism § Prism – Is a polyhedron with exactly 2 , // faces, called bases. § Name it by the shape of its bases. Bases are Rectangles: Lateral Faces – All faces that are not bases. (Sides)

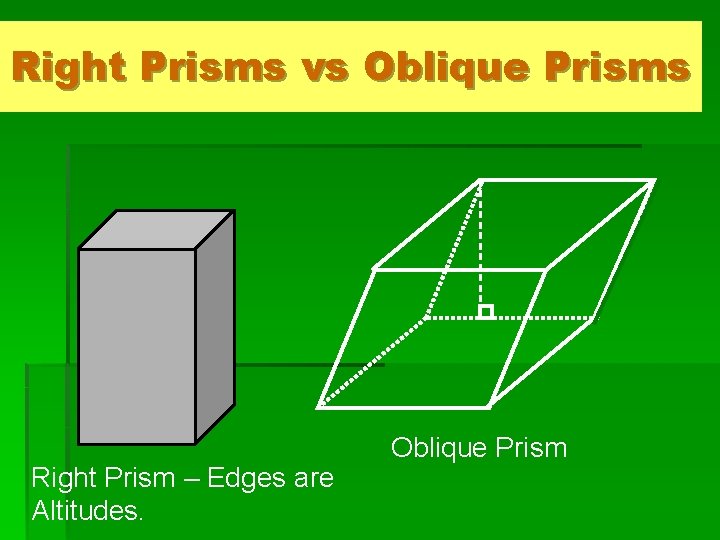
Right Prisms vs Oblique Prisms Right Prism – Edges are Altitudes. Oblique Prism

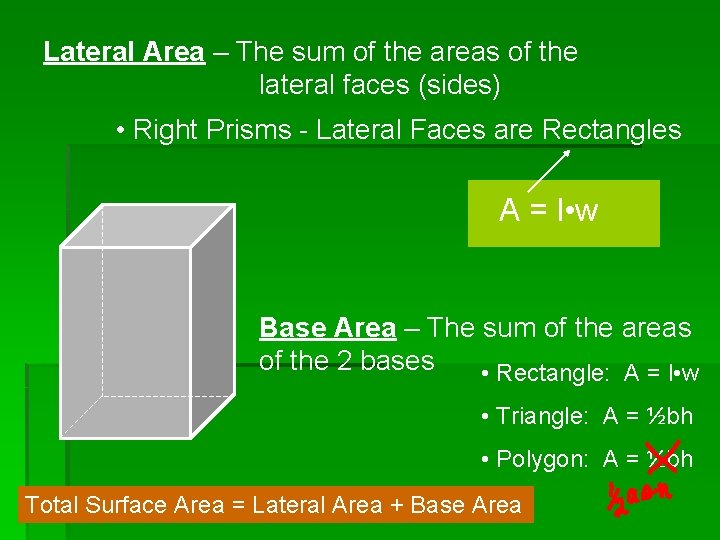
Lateral Area – The sum of the areas of the lateral faces (sides) • Right Prisms - Lateral Faces are Rectangles A = l • w Base Area – The sum of the areas of the 2 bases • Rectangle: A = l • w • Triangle: A = ½bh • Polygon: A = ½bh Total Surface Area = Lateral Area + Base Area

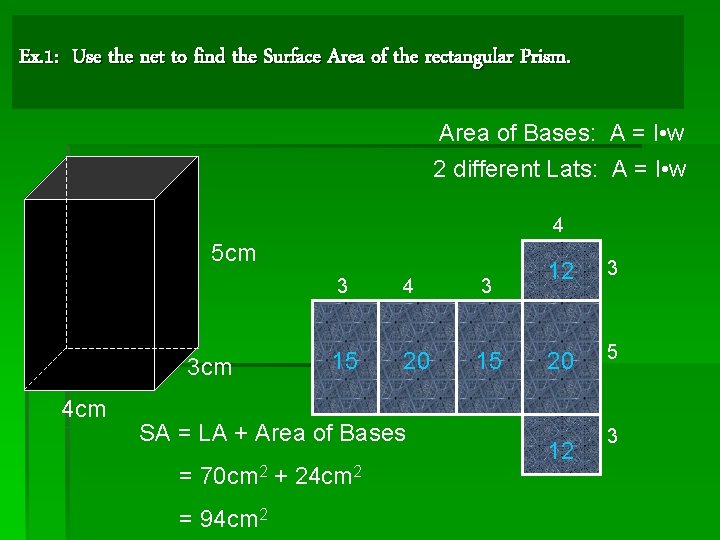
Ex. 1: Use the net to find the Surface Area of the rectangular Prism. Area of Bases: A = l • w 2 different Lats: A = l • w 4 5 cm 3 cm 4 cm 3 4 3 15 20 15 SA = LA + Area of Bases = 70 cm 2 + 24 cm 2 = 94 cm 2 12 3 20 5 12 3

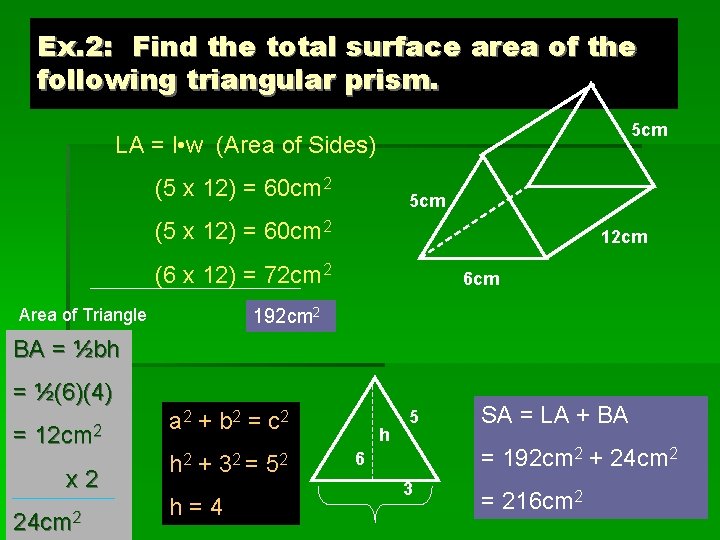
Ex. 2: Find the total surface area of the following triangular prism. 5 cm LA = l • w (Area of Sides) (5 x 12) = 60 cm 2 5 cm (5 x 12) = 60 cm 2 12 cm (6 x 12) = 72 cm 2 Area of Triangle 6 cm 192 cm 2 BA = ½bh = ½(6)(4) = 12 cm 2 x 2 24 cm 2 a 2 + b 2 = c 2 h 2 + 32 = h=4 52 h 5 SA = LA + BA = 192 cm 2 + 24 cm 2 6 3 = 216 cm 2

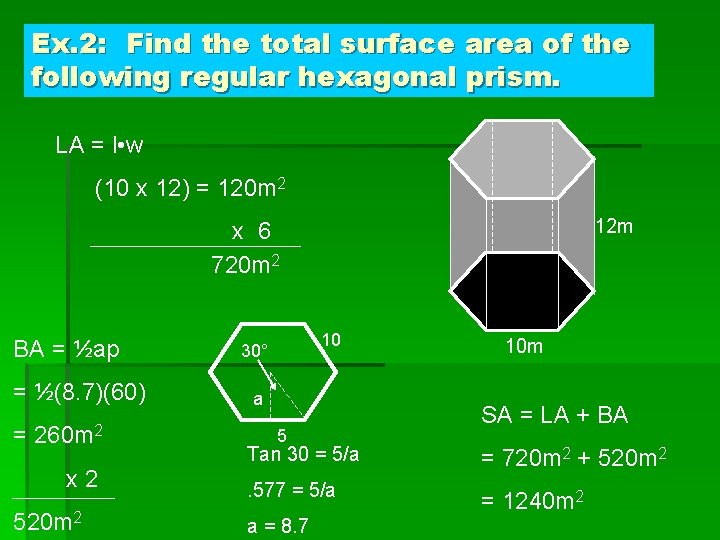
Ex. 2: Find the total surface area of the following regular hexagonal prism. LA = l • w (10 x 12) = 120 m 2 12 m x 6 720 m 2 BA = ½ap = ½(8. 7)(60) = 260 m 2 x 2 520 m 2 10 30° a 5 10 m SA = LA + BA Tan 30 = 5/a = 720 m 2 + 520 m 2 . 577 = 5/a = 1240 m 2 a = 8. 7

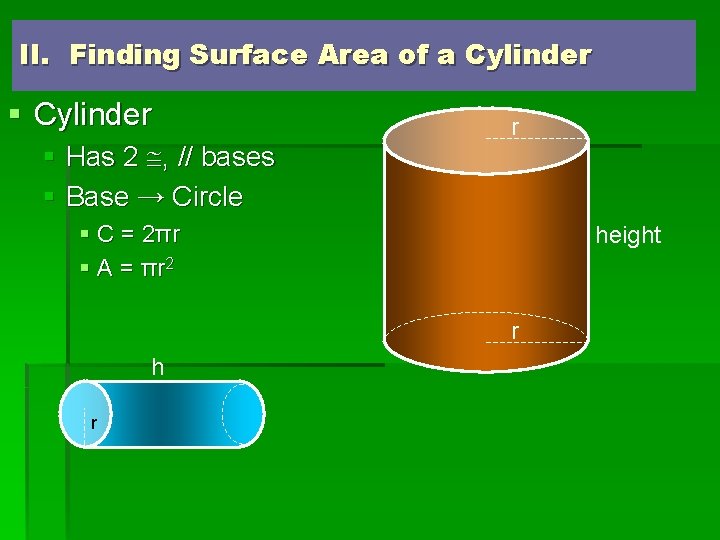
II. Finding Surface Area of a Cylinder § Has 2 , // bases § Base → Circle r § C = 2 πr § A = π r 2 height r h r

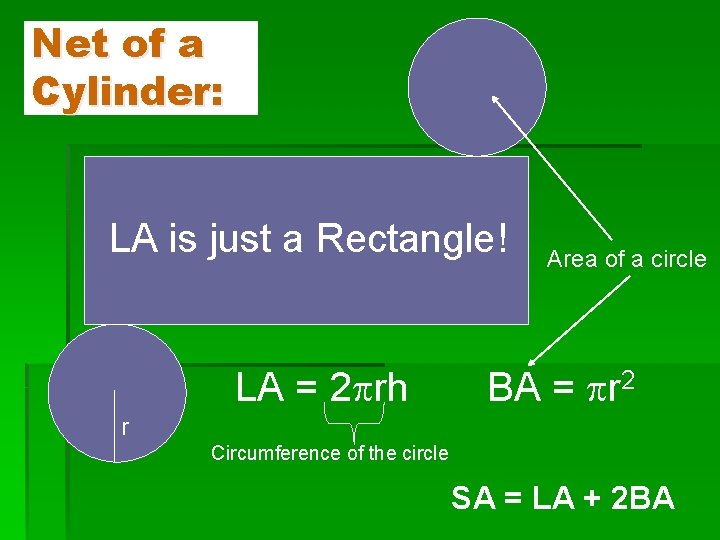
Net of a Cylinder: LA is just a Rectangle! LA = 2 rh Area of a circle BA = r 2 r Circumference of the circle SA = LA + 2 BA

Ex. 4: SA of a right cylinder LA = 2 rh 6 ft 9 ft = 2 (6)(9) Area of Base = 108 ft 2 BA = r 2 = 339. 3 ft 2 = (6)2 = 36 ft 2 x 2 SA = LA + BA = 72 ft 2 = 339. 3 ft 2 + 226. 2 ft 2 = 226. 2 ft 2 = 565. 5 ft 2

What did I learn today? ? § Find the area of the lateral sides first!! § Usually rectangles § Be careful, the rectangles are not always the same size. § Second, find the area of the Base § Rectangle, Triangle, Polygon, or a Circle § There always 2 bases in prisms. § Multiply by 2!