ANALISIS TANGGAP TRANSIEN ANALISIS TANGGAP TRANSIEN Langkah pertama

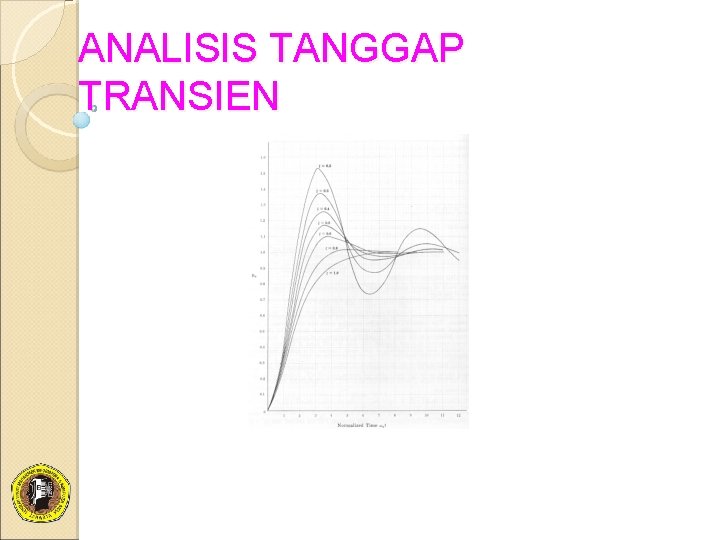
ANALISIS TANGGAP TRANSIEN

ANALISIS TANGGAP TRANSIEN Langkah pertama dalam menganalisis sistem kendali adalah menurunkan model matematik sistem. � Setelah model diperoleh, kita dapat menggunakan berbagai metode untuk analisis keandalan sistem (system performance). � Respon waktu sistem kendali terdiri dari dua bagian: 1. Tanggap Keadaan Tunak (Seady State response) adalah perilaku keluaran sistem jika waktu mendekati tak-terhingga. 2. Tanggap Transien (Transient Response) adalah tanggap sistem yang berlangsung dari keadaan awal sampai keadaan akhir. � Dalam merancang sistem kendali, kita harus mampu meramal perilaku dinamik sistem dengan mengetahui komponen sistem. � Karakteristik perilaku dinamik sistem kendali yang paling penting adalah kestabilan mutlak, yang mencirikan bahwa sistem stabil atau tidak stabil.

Soal Tanggap total y(t) dari persamaan diferensial: dengan kondisi awal y(0)=0 dan Tentukan tanggap keadaan tunak dan tanggap transiennya. Jawab: ya(t) = c 1 e-t + c 2 e-2 t Dengan memasukkan kondisi awal, maka: ya(0) = y(0) = 0 = c 1 + c 2 Maka diperoleh : c 1=1 dan c 2=-1

Sehingga diperoleh persamaan: ya(t) = e-t - e-2 t Tanggap dipaksa (forced response - integral konvoluasi): Tanggap total : y(t) = ya(t) + yb(t) = (e-t - e-2 t)+½(1 – 2 e-t + e-2 t) = ½ – ½e-2 t) Tanggap Keadaan Tunak : Tanggap Transien :

FUNGSI TANGGAP IMPULSA � Fungsi alih: G(s) = Y(s)/X(s) dimana : X(s) adalah transformasi Laplace masukkan dan Y(s) adalah transformasi Laplace keluaran. � Dapat ditulis: Y(s) = G(s)X(s) yaitu perkalian dalam domain kompleks ekivalen dengan konvolusi dalam domain waktu. � Transformasi Laplace balik adalah integral konvolusi berikut: dimana g(t) = x(t) = 0 untuk t < 0 n Fungsi tanggap impulsa merupakan tanggap sistem linier tarhadap satuan impulsa apabila keadaan awalnya nol. Y(s) = G(s) y(t) = g(t) = fungsi tanggap impulsa

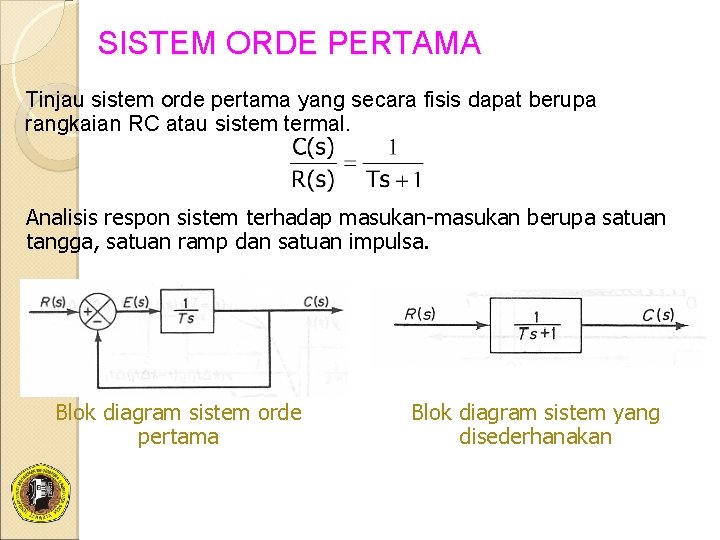
SISTEM ORDE PERTAMA Tinjau sistem orde pertama yang secara fisis dapat berupa rangkaian RC atau sistem termal. Analisis respon sistem terhadap masukan-masukan berupa satuan tangga, satuan ramp dan satuan impulsa. Blok diagram sistem orde pertama Blok diagram sistem yang disederhanakan

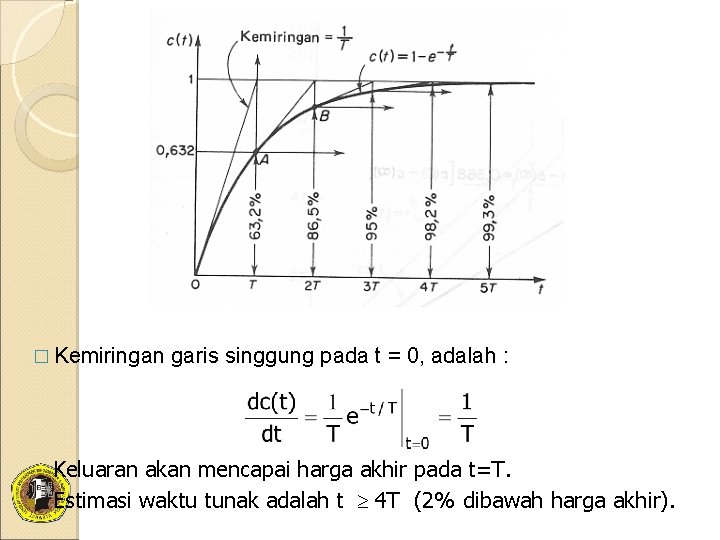
Tanggap Tangga � Transformasi Laplace dari fungsi masukan tangga adalah 1/s, persamaan kita peroleh menjadi: n Dengan menguraikan C(s) menjadi pecahan parsial, kita peroleh: n Dengan melakukan transformasi Laplace bali, kita peroleh: n n n Keluaran c(t) mula-mula nol kemudian akhirnya menjadi satu. Pada t=T, harga c(t) adalah 0, 632 (63, 2% perubahan total). c(T) = 1 – e-1 = 0, 632 Pada t=2 T, harga c(t)=86, 5%

� Kemiringan n garis singgung pada t = 0, adalah : Keluaran akan mencapai harga akhir pada t=T. Estimasi waktu tunak adalah t 4 T (2% dibawah harga akhir).

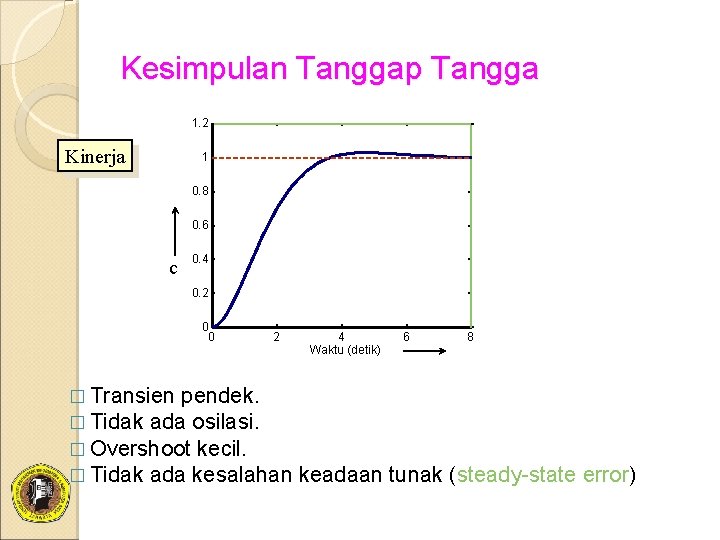
Kesimpulan Tanggap Tangga 1. 2 Kinerja 1 0. 8 0. 6 c 0. 4 0. 2 0 0 2 � Transien pendek. � Tidak ada osilasi. � Overshoot kecil. � Tidak ada kesalahan 4 Waktu (detik) 6 8 keadaan tunak (steady-state error)

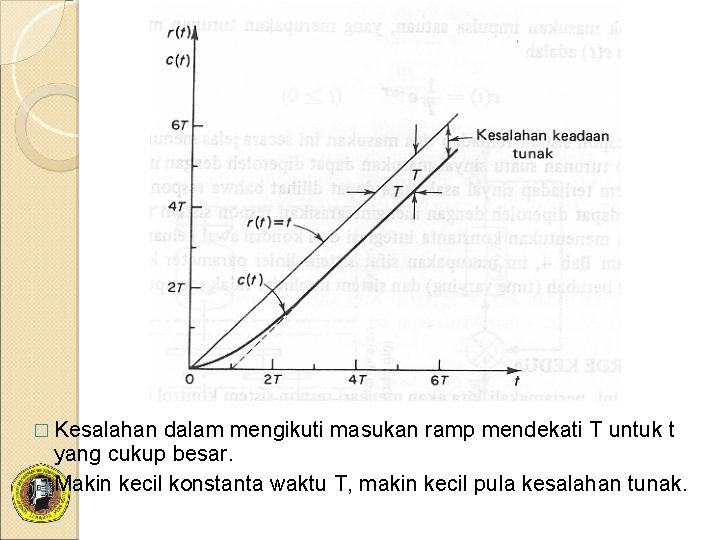
Tanggap Ramp � Transformasi Laplace dari fungsi masukan ramp adalah 1/s 2 , persamaan kita peroleh menjadi: n Dengan menguraikan C(s) menjadi pecahan parsial, kita peroleh: n Dengan melakukan transformasi Laplace bali, kita peroleh: n Sinyal kesalahan e(t) adalah n Jika t mendekati tak terhingga, maka e-t/T mendekati nol, sehingga sinyal kesalahan e(t) mendekati T atau : e( ) = T

� Kesalahan dalam mengikuti masukan ramp mendekati T untuk t yang cukup besar. � Makin kecil konstanta waktu T, makin kecil pula kesalahan tunak.

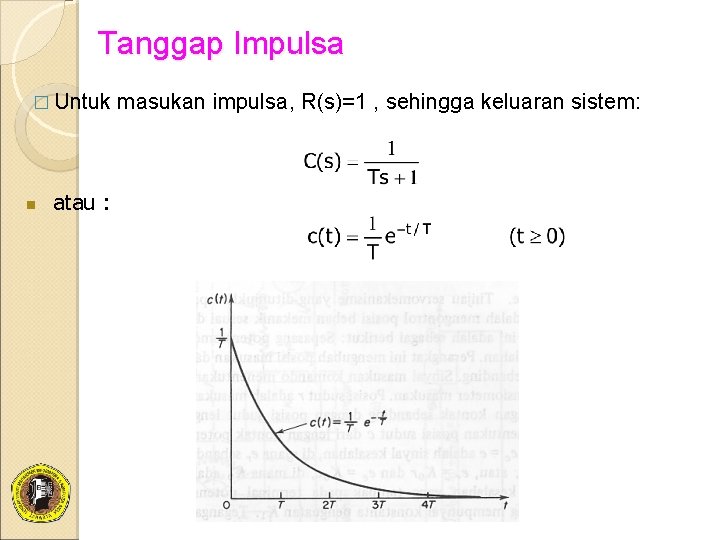
Tanggap Impulsa � Untuk n atau : masukan impulsa, R(s)=1 , sehingga keluaran sistem:

SISTEM ORDE KEDUA Dalam studi sistem kendali, persamaan diferensial orde kedua ditulis: dengan konstanta adalah damping ratio dan konstanta n adalah undamped natural frequency. Jika 0 1, maka persamaan karakteristik adalah : Akar-akarnya adalah : a adalah inverse dari konstanta waktu dari sistem ( = 1/a)

Contoh Sistem Order Dua

Parameter Sistem Orde Dua

Fungsi bobot dari persamaan diferensial orde kedua adalah : Tanggap unit tangga dinyatakan dengan: dengan :

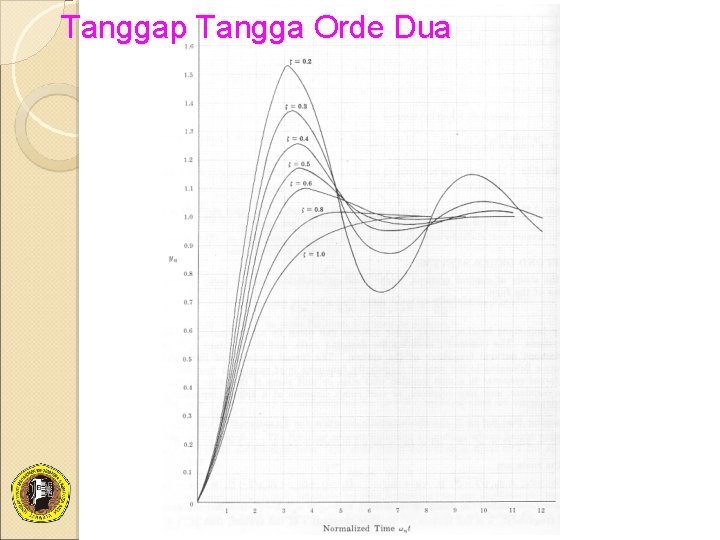
Tanggap Tangga Orde Dua

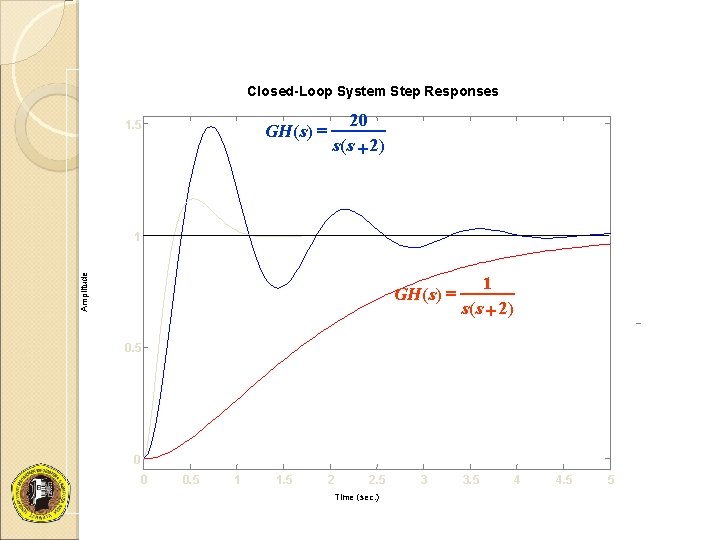
Closed-Loop System Step Responses GH ( s) = 1. 5 20 s( s + 2) Amplitude 1 GH ( s) = 1 s( s + 2) 0. 5 0 0 0. 5 1 1. 5 2 2. 5 Time (sec. ) 3 3. 5 4 4. 5 5

Tanggap Tangga � Diketahui sistem: n Tanggap tangga: n Kutub-kutub: Im s 1 = 0 s 2 = - n + j n 1 - 2 s 3 = - n - j n 1 - 2 Re

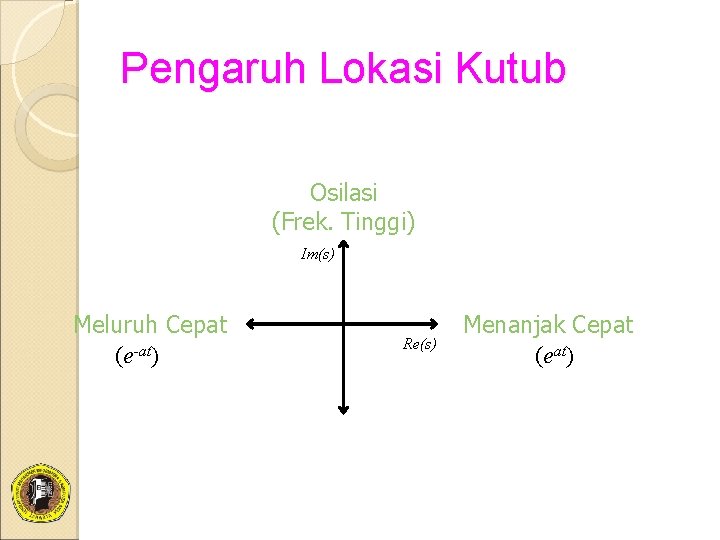
Pengaruh Lokasi Kutub Osilasi (Frek. Tinggi) Im(s) Meluruh Cepat (e-at) Re(s) Menanjak Cepat (eat)

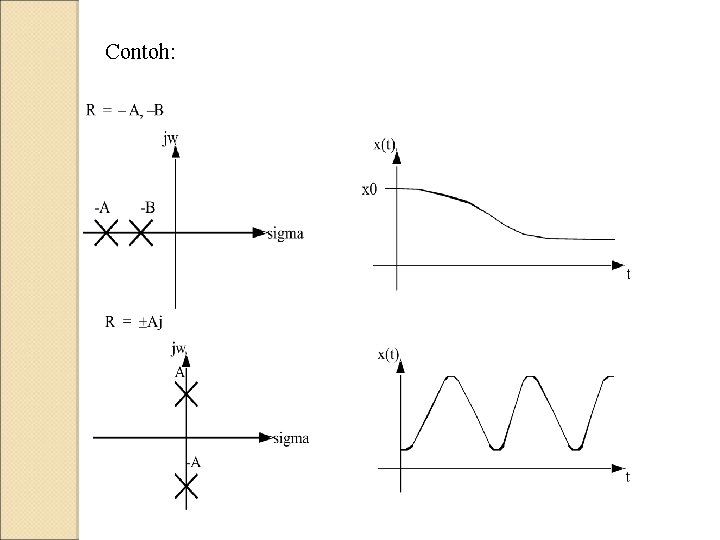
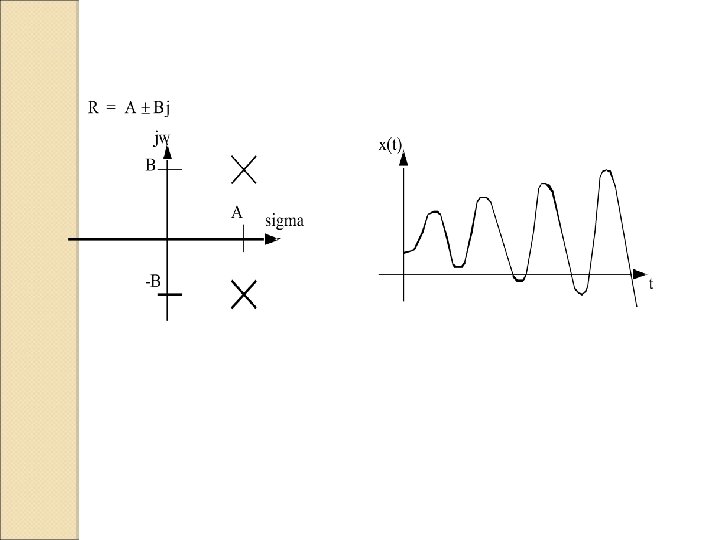
Contoh:

Tanggap Tangga Sistem Orde Dua � Diketahui sistem: n Dengan menguraikan C(s) menjadi pecahan parsial, kita peroleh: n Maka tanggap waktu :

Kutub-kutub Nyata dan Kompleks � Jika diketahui fungsi tanggap kompleks: n Maka fungsi tanggap waktunya adalah: n Bentuk umum dari fungsi tanggap waktu:

Soal � Diketahui fungsi alih sistem: n Tentukan fungsi tanggap tangga dan tanggap waktunya. Jawab: n Tanggap tangga: n Dengan menguraikan C(s) menjadi pecahan parsial, kita peroleh: n

n Maka: n Maka fungsi tanggap waktunya adalah:

SPESIFIKASI TANGGAP TRANSIEN � Tanggap transien sistem kendali sering menunjukkan osilasi terendam sebelum mencapai keadaan tunak. � Karakteristik tanggap transien sistem kontrol terhadap masukan unit tangga, dinyatakan dalam parameter: ◦ Waktu tunda (delay time) td ◦ Waktu naik (rise time) tr ◦ Waktu puncak (peak time) tp ◦ Lewatan maksimum (maksimum overshoot) Mp ◦ Waktu penetapan (settling time) ts

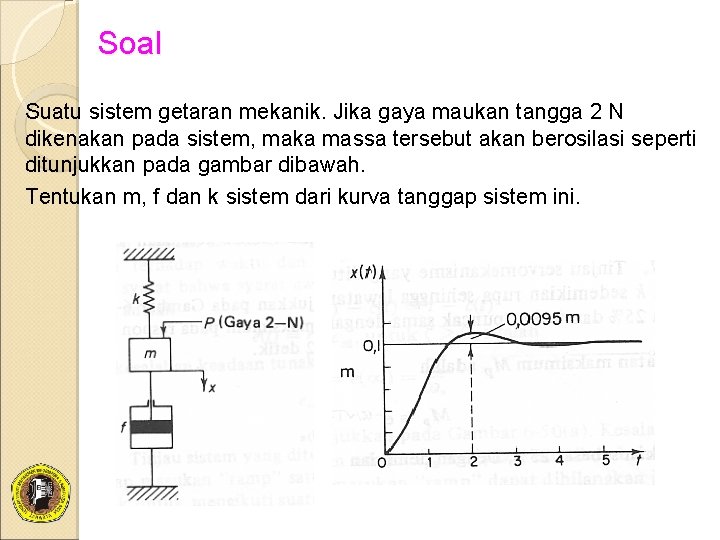
Soal Suatu sistem getaran mekanik. Jika gaya maukan tangga 2 N dikenakan pada sistem, maka massa tersebut akan berosilasi seperti ditunjukkan pada gambar dibawah. Tentukan m, f dan k sistem dari kurva tanggap sistem ini.

Jawab � Fungsi alih sistem adalah: n karena: n Maka tanggap tangga: n Ini berarti bahwa harga keadaan tunak x adalah: n Dengan demikian: k = 20 N/m n Perhatikan bahwa Mp = 9, 5% untuk =0, 6. Waktu puncak tp diberikan oleh :

n Kurva eksperimental menunjukkan bahwa tp = 2 detik, maka: n Karena: n Maka diperoleh: n Selanjutnya f ditentukan dari :

KRITERIA KESTABILAN ROUTH � Suatu sistem kendali adalah stabil jika dan hanya jika semua kutub loop tertutup terletak disebelah sumbu khayal bidang s. � Sebagian besar sistem loop tertutup linier mempunyai fungsi alih: dimana a dan b adalah konstanta dan m n, maka kita harus mengurai polinomial A(s) atas faktor-faktornya untuk mencari kutub-kutub tertutup. n n Kriteria kestabilan Routh menunjukkan ada atau tidak ada akar positif pada persamaan polinominal, tanpa harus menyelesaikan persamaan tersebut. Informasi mengenai kestabilan diperoleh secara langsung dari koefisien-koefisien persamaan karakteristik.

Prosedur Kriteria Kestabilan Routh � Tulislah n n polinomial dalam s sesuai dengan bentuk berikut: Kriteria diterapkan menggunakan Tabel Routh yang didefinisikan sebagai berikut: Koefisien-koefisien b 1, b 2, b 3 dan seterusnya dihitung dengan:

n Syarat perlu dan cukup bahwa semua akar-akar persamaan berada disebelah kiri sumbu khayal bidang s adalah bahwa semua koefisien persamaan harus positif dan semua suku pada kolom pertama dari susunan tersebut harus bertanda positif.

Soal Tinjau polinomial berikut: s 3 + 6 s 2 + 12 s + 8 = 0 Tentukan kestabilan sistem berdasarkan kriteria kestabilan Routh. Jawab: n Karena tidak ada perubahan tanda koefisien pada kolom pertama dari tabel, berarti seluruh akar-akar persamaan adalah bagian nyata negatif (sistem stabil).