Analisi delle osservazioni II parte Lezioni di Fondamenti


























- Slides: 41

Analisi delle osservazioni II parte Lezioni di Fondamenti e metodi per l’analisi empirica nelle scienze sociali

Descrizione e spiegazione Descrizione v. Analisi statistica monovariata (misure di sintesi e misure di dispersione) v. Modelli probabilistici v. Distribuzioni note di probabilità (uniforme, normale, ecc. ) 2 Spiegazione v Analisi bivariata v Analisi multivariata Relazione tra due o più fenomeni sociali g. fanci@unimc. it A. A. 2015 - 2016

Analisi delle osservazioni Caratteristiche logicomatematiche Informazioni 3 Procedura Analisi Dati g. fanci@unimc. it A. A. 2015 - 2016

Descrizione Matrice casi per variabili: �l’unità di analisi deve essere sempre la stessa �su tutti i casi deve essere rilevata la stessa informazione Codifica Operazione di traduzione del materiale empirico grezzo in matrice dati 4 g. fanci@unimc. it A. A. 2015 - 2016

Esempio matrice dati o casi per variabili 5 g. fanci@unimc. it A. A. 2015 - 2016

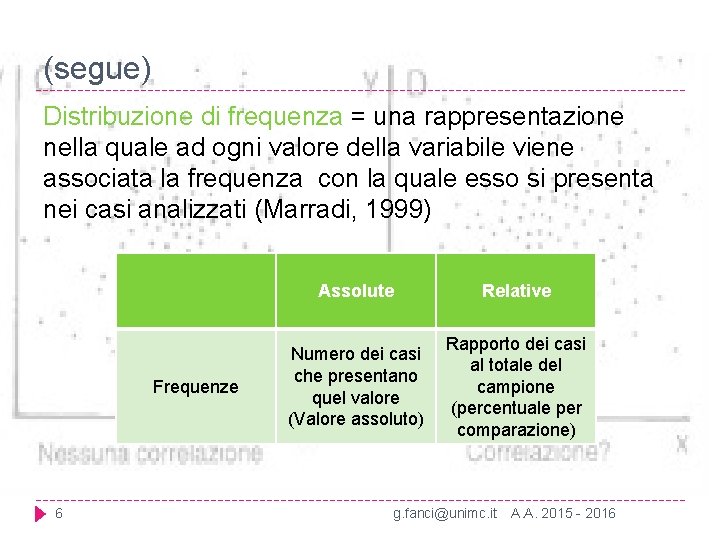
(segue) Distribuzione di frequenza = una rappresentazione nella quale ad ogni valore della variabile viene associata la frequenza con la quale esso si presenta nei casi analizzati (Marradi, 1999) Frequenze 6 Assolute Relative Numero dei casi che presentano quel valore (Valore assoluto) Rapporto dei casi al totale del campione (percentuale per comparazione) g. fanci@unimc. it A. A. 2015 - 2016

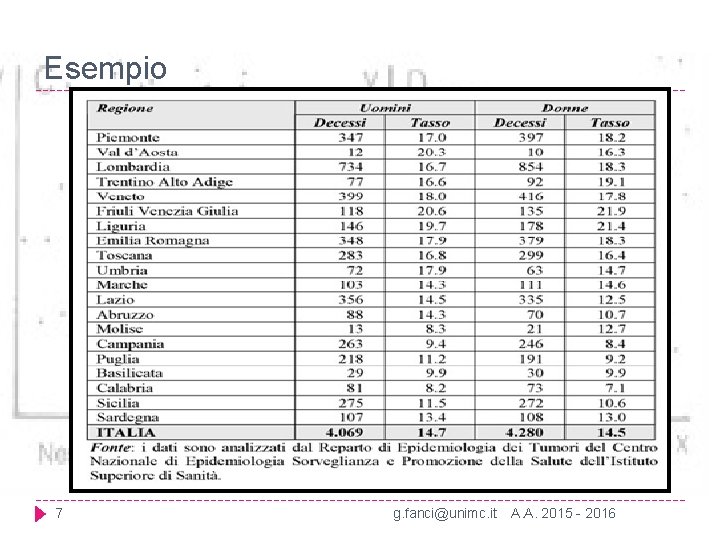
Esempio 7 g. fanci@unimc. it A. A. 2015 - 2016

Analisi monovariata Misure di sintesi Moda, Mediana e Media 8 g. fanci@unimc. it A. A. 2015 - 2016

Misure di sintesi e variabili Ogni variabile ha la sua misura di sintesi = BARICENTRO dei suoi valori. q MODA: modalità che si presenta con maggior frequenza; variabili nominali; q MEDIANA: modalità del caso che occupa il posto di mezzo nella distribuzione ordinata dei casi secondo quella variabile; variabili ordinali; N dispari = N+1/2; N pari = N/2 e N/2 + 1; q MEDIA: somma dei valori assunta dalla variabile su tutti i casi divisa per il numero di casi; variabili cardinali. 9 g. fanci@unimc. it A. A. 2015 - 2016

Rappresentazioni grafiche delle distribuzioni Nominali • Diagrammi a barre • Diagrammi di composizione 10 Cardinali • Istogramma • Poligono di frequenza g. fanci@unimc. it A. A. 2015 - 2016

Per le variabili nominali 11 g. fanci@unimc. it A. A. 2015 - 2016

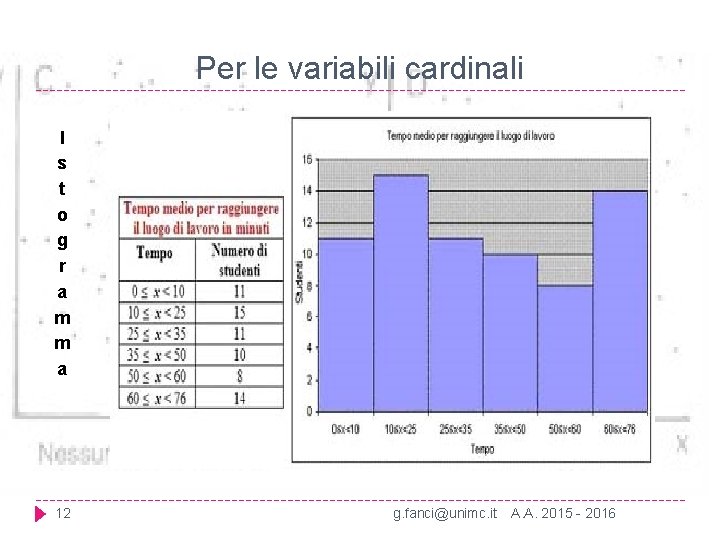
Per le variabili cardinali I s t o g r a m m a 12 g. fanci@unimc. it A. A. 2015 - 2016

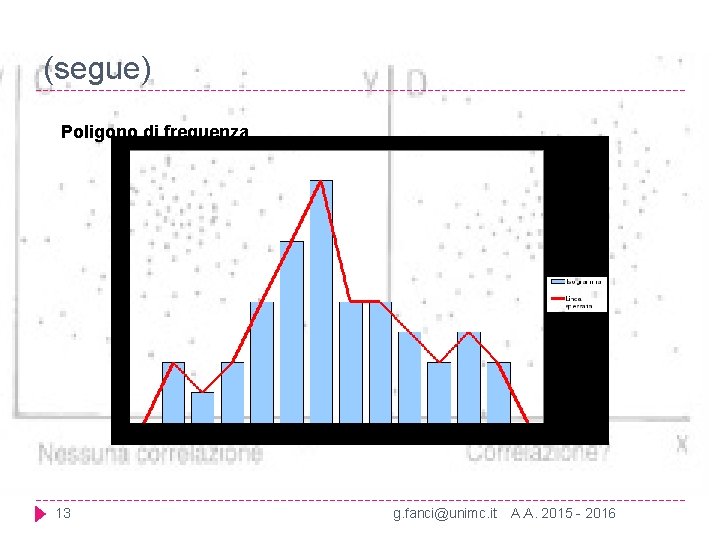
(segue) Poligono di frequenza 13 g. fanci@unimc. it A. A. 2015 - 2016

Relazioni tra variabili Si osserva una covariazione tra due fenomeni, ossia che variano insieme; es. : al variare del titolo di studio varia il reddito. Due considerazioni: 1. Si tratta di relazioni statistiche, ossia di tipo probabilistico: è più probabile che un individuo con laurea guadagni di più, ma possono esserci eccezioni; 2. La ricerca consente di osservare la covariazione, ma la interpretazione causale spetta al ricercatore: “covariazione non significa causazione”. 14 g. fanci@unimc. it A. A. 2015 - 2016

Dipendente / Indipendente • classe Variabile dipendente sociale /orientamento politico; • educazione /pregiudizio razziale; • età / atteggiament o religioso Variabile indipendente 15 g. fanci@unimc. it A. A. 2015 - 2016

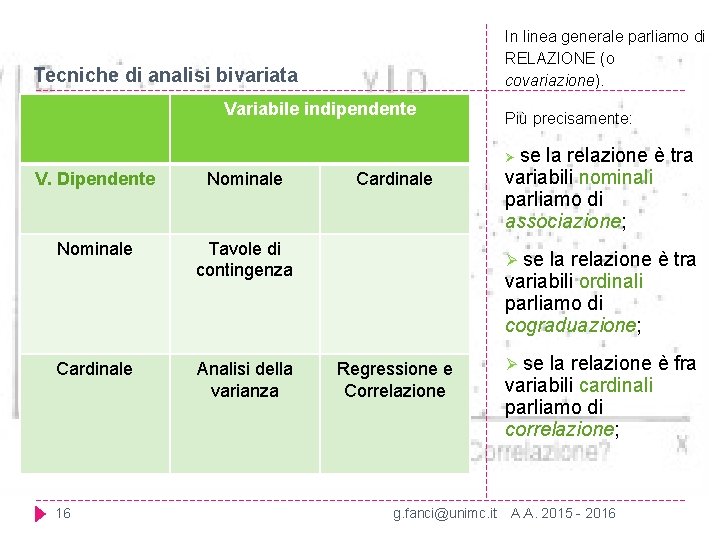
In linea generale parliamo di RELAZIONE (o covariazione). Tecniche di analisi bivariata Variabile indipendente Più precisamente: se la relazione è tra variabili nominali parliamo di associazione; Ø V. Dipendente Nominale Tavole di contingenza Cardinale Analisi della varianza 16 Cardinale se la relazione è tra variabili ordinali parliamo di cograduazione; Ø Regressione e Correlazione g. fanci@unimc. it se la relazione è fra variabili cardinali parliamo di correlazione; Ø A. A. 2015 - 2016

Tavole di contingenza: associazione � Occorre innanzitutto osservare congiuntamente le due distribuzioni di frequenza Ossia bisogna organizzare le osservazioni in una tabella a doppia entrata (o tavola di contingenza) in grado di mostrare congiuntamente le modalità delle due variabili 17 g. fanci@unimc. it A. A. 2015 - 2016

Esempio tavola di contingenza (contingent in inglese significa “condizionata” ) W = gradimento (dipendente); X = genere (indipendente) W 18 X Basso w 1 Medio w 2 Alto w 3 somma S Femmina x 1 4 (n 1, 1) 3 (n 1, 2) 4 (n 1, 3) 11 n 1. Maschio x 2 4 (n 2, 1) 2 (n 2, 2) 3 (n 2, 3) 9 n 2. somma S 8 n. 1 5 n. 2 7 n. 3 20 N g. fanci@unimc. it A. A. 2015 - 2016

Riflessioni sulla tabella � Distribuzione congiunta di X e di W: frequenze congiunte assolute N con doppio pedice; � Distribuzione marginale di X: la prima e l’ultima colonna eliminando l’effetto di W; � Distribuzione marginale di W: la prima e l’ultima riga eliminando l’effetto di X; � Percentuali di riga; � Percentuali di colonna. 19 g. fanci@unimc. it A. A. 2015 - 2016

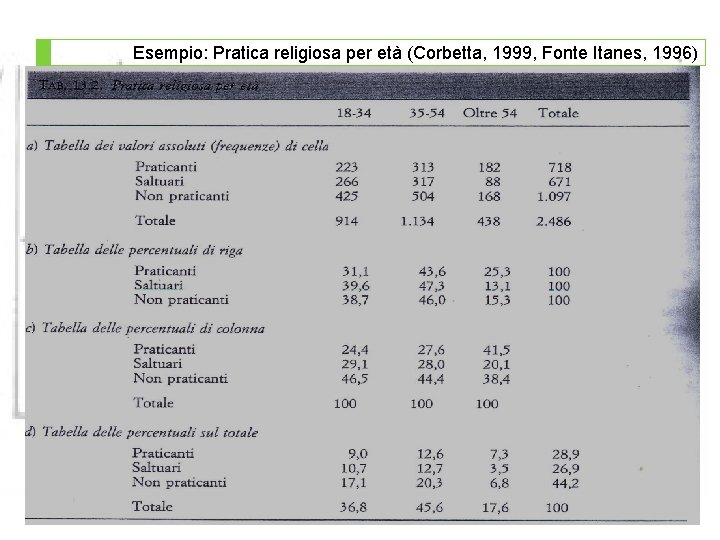
Esempio: Pratica religiosa per età (Corbetta, 1999, Fonte Itanes, 1996) 20 g. fanci@unimc. it A. A. 2015 - 2016

Come scegliere la percentuale? � Si sceglie la percentuale di colonna quando si vuole analizzare l’influenza che la variabile posta in colonna ha sulla variabile posta in riga; � Si sceglie la percentuale di riga quando si vuole analizzare l’influenza che la variabile posta in riga ha sulla variabile posta in colonna Si definisce qual è la variabile indipendente e si percentualizza all’interno della sua modalità. 21 g. fanci@unimc. it A. A. 2015 - 2016

Regressione: correlazione Se la relazione interessa due variabili cardinali parliamo di correlazione e ci serviamo della retta di regressione come modello matematico. Rappresentazione grafica: piano cartesiano: cartesiano � Sulla retta orizzontale – chiamata delle ascisse – si pone, per convenzione, convenzione la variabile che si assume essere indipendente, talvolta detta esplicativa; esplicativa � Sulla retta verticale – chiamata delle ordinate – si pone, per convenzione, convenzione la variabile che si assume essere dipendente. 22 g. fanci@unimc. it A. A. 2015 - 2016

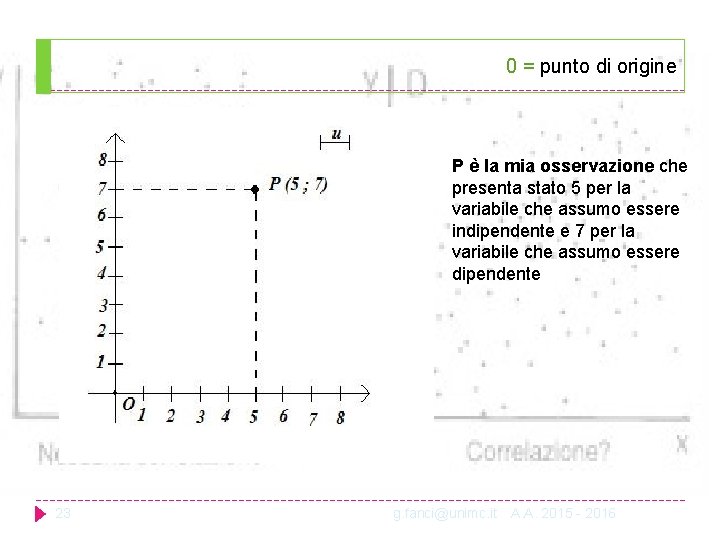
0 = punto di origine P è la mia osservazione che presenta stato 5 per la variabile che assumo essere indipendente e 7 per la variabile che assumo essere dipendente 23 g. fanci@unimc. it A. A. 2015 - 2016

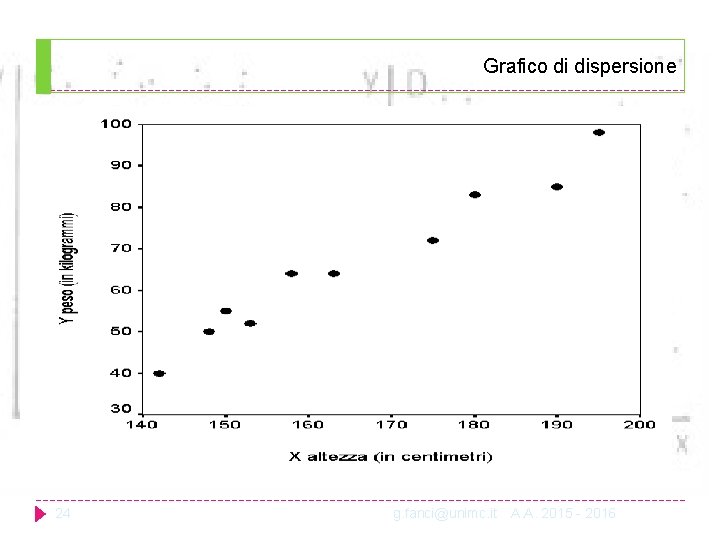
Grafico di dispersione 24 g. fanci@unimc. it A. A. 2015 - 2016

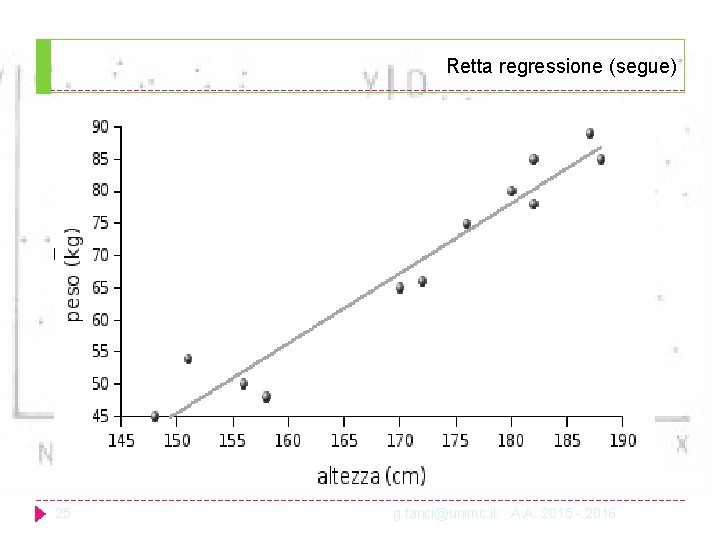
Retta regressione (segue) 25 g. fanci@unimc. it A. A. 2015 - 2016

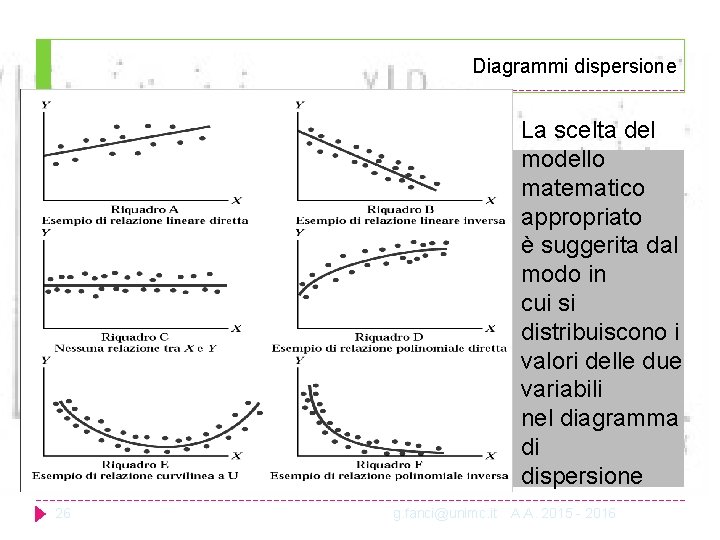
Diagrammi dispersione La scelta del modello matematico appropriato è suggerita dal modo in cui si distribuiscono i valori delle due variabili nel diagramma di dispersione 26 g. fanci@unimc. it A. A. 2015 - 2016

Relazione lineare bivariata “Regrediamo” Y rispetto ad X Regressione bivariata, in termini algebrici Y = a + b. X Dove a indica una costante, punto in cui la retta “intercetta” o incrocia l’asse verticale; b indica il coefficiente di regressione, ossia l’inclinazione della retta; Si dice che la retta interpola, meglio di altre forme, i punti (le osservazioni) e sintetizza la nuvola. 27 g. fanci@unimc. it A. A. 2015 - 2016

Equazione predittiva Predire Y da X Posso conoscere la variazione di Y se, come e quando varia X Valore assunto da Y per ciascuna osservazione i è funzione lineare esatta del corrispondente valore di X Ŷi = a + byx Xi 28 g. fanci@unimc. it A. A. 2015 - 2016

Modello di regressione lineare La difficoltà maggiore è quella di non riuscire a rappresentare relazioni bivariate con una retta perfettamente interpolante. occorre stimare le deviazioni dalla predizione lineare Yi = a + byx Xi + ei Dove ei rappresenta la porzione di valore di Y per l’osservazione i che non è predetta dalla sua relazione lineare con X. 29 g. fanci@unimc. it A. A. 2015 - 2016

Y e 1 X Valore osservato i-esimo Valore medio della distribuzione Valore predetto i-esimo Errore i-esimo A. A. 2015 - 2016 g. fanci@unimc. it 30

Y e 1 X e 1 10 – 12 = (10 – 5) + (5 – 12) A. A. 2015 - 2016 g. fanci@unimc. it 31

Errore o residuo Si chiama residuo per indicare lo scarto fra il valore atteso o predetto dall’equazione di regressione e il valore effettivamente osservato Y–Ŷ=e Y – Ŷ = [a + byx Xi + ei ] – [a + byx Xi ] = ei 32 g. fanci@unimc. it A. A. 2015 - 2016

Stima della equazione di regressione stimare valori dei due coefficienti con le osservazioni le stime di a e bxy devono minimizzare gli errori, “fare sì che gli errori di predizione prodotti da quella equazione siano minori di quelli prodotti da qualsiasi relazione lineare” (Knoke) I due coefficienti devono soddisfare il criterio dei minimi quadrati: quadrati “la migliore retta sia quella che rende minima la somma delle differenze al quadrato tra i valori di yi realmente osservati e i corrispondenti valori che la retta stessa fornisce per i diversi valori di xi osservati” 33 g. fanci@unimc. it A. A. 2015 - 2016

Retta detta anche dei minimi quadrati � La somma dei residui è sempre = 0, se la elevo al quadrato il valore sarà sempre positivo � “Sommando le differenze al quadrato fra ogni valore osservato di Yi e il corrispondente valore Ŷi predetto dall’equazione di regressione prescelta si dovrebbe ottenere una quantità minore di quella che si otterrebbe utilizzando qualsiasi altra equazione di regressione lineare” (Knoke) 34 g. fanci@unimc. it A. A. 2015 - 2016

Devianza spiegata e devianza non spiegata 35 g. fanci@unimc. it A. A. 2015 - 2016

Coefficiente ρ di Bravais Pearson Il coefficiente di correlazione lineare ρ misura l’intensità del legame lineare (interpretabile graficamente da una retta) tra due variabili cardinali X e Y, ovvero il grado di proporzionalità esistente tra X e Y. Si calcola come rapporto tra covarianza tra X e Y e il rapporto degli scarti quadratici medi: ρxy = covxy σx σy ρ = + 1, correlazione perfetta positiva ρ = - 1 , correlazione perfetta negativa 36 g. fanci@unimc. it A. A. 2015 - 2016

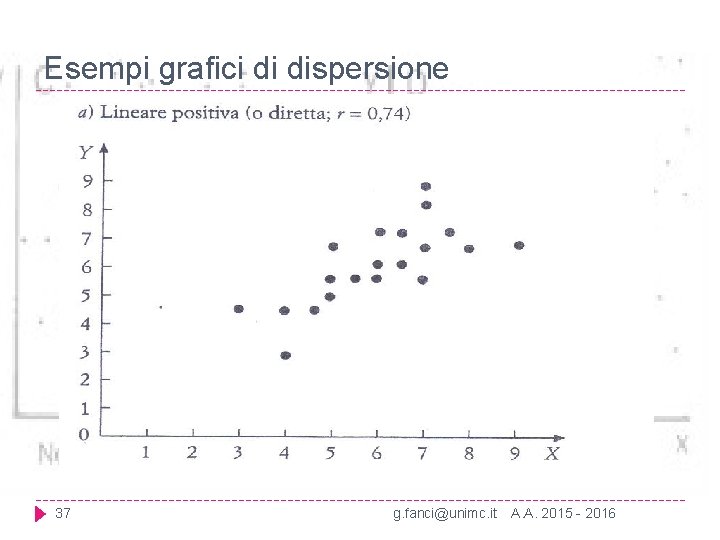
Esempi grafici di dispersione 37 g. fanci@unimc. it A. A. 2015 - 2016

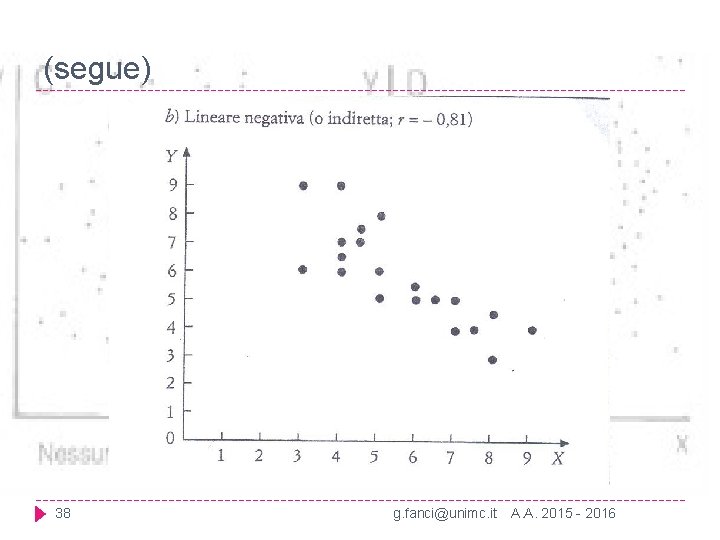
(segue) 38 g. fanci@unimc. it A. A. 2015 - 2016

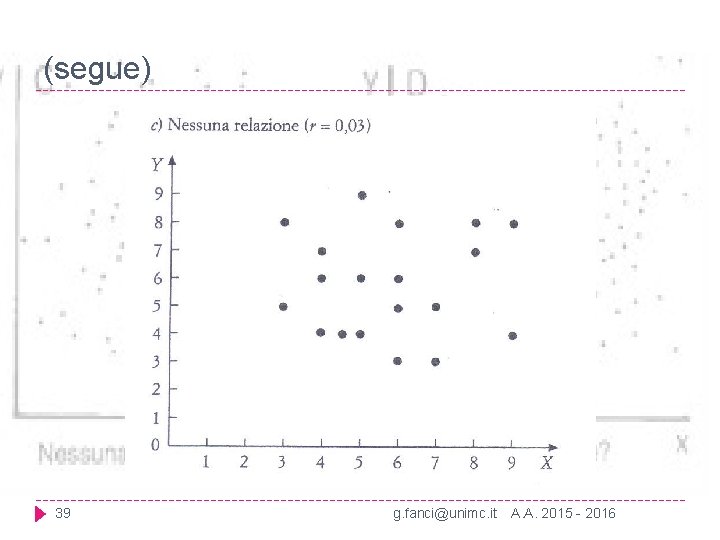
(segue) 39 g. fanci@unimc. it A. A. 2015 - 2016

Coefficiente di determinazione Corrisponde a ρ di Pearson al quadrato, fornisce la stima della varianza spiegata di una variabile da parte dell’altra. ρ2 = σ x y 2 σ x 2σ y 2 0 > ρ2 > 1 È una misura della capacità della retta di regressione di rappresentare la nube di punti del diagramma di dispersione. Quanto più i punti sono lontani dalla retta tanto più ρ2 tende a 0; più sono vicini più si approssima a 1. ρ2 = 0, la retta non è la rappresentazione migliore, forse la relazione c’è ma è più adeguata un’altra figura. 40 g. fanci@unimc. it A. A. 2015 - 2016

(segue) 41 g. fanci@unimc. it A. A. 2015 - 2016
 Lezioni di tecnica delle costruzioni
Lezioni di tecnica delle costruzioni Barriere e facilitatori nel contesto scolastico
Barriere e facilitatori nel contesto scolastico Barriere e facilitatori infanzia
Barriere e facilitatori infanzia Fondamenti di automatica benvenuti
Fondamenti di automatica benvenuti Fondamenti di astronomia
Fondamenti di astronomia I fondamenti dell'ict
I fondamenti dell'ict Fondamenti di informatica 2
Fondamenti di informatica 2 Fondamenti di informatica 2
Fondamenti di informatica 2 Pedagogia generale slide
Pedagogia generale slide Giddens fondamenti di sociologia
Giddens fondamenti di sociologia Giovanni danese
Giovanni danese Reazione di riduzione
Reazione di riduzione Naturalismo francese e verismo italiano
Naturalismo francese e verismo italiano Fondamenti di misure
Fondamenti di misure Fondamenti di automatica unife
Fondamenti di automatica unife Fondamenti biogenetici
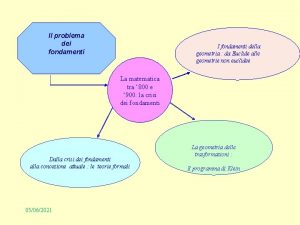
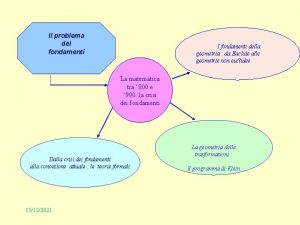
Fondamenti biogenetici Crisi dei fondamenti
Crisi dei fondamenti La nascita delle lingue e delle letterature romanze
La nascita delle lingue e delle letterature romanze L'esperienza delle cose moderne e la lezione delle antique
L'esperienza delle cose moderne e la lezione delle antique L'esperienza delle cose moderne
L'esperienza delle cose moderne Lim fa parte delle ict
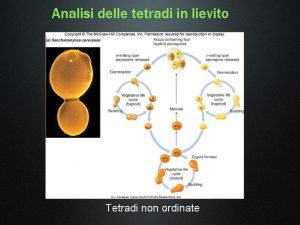
Lim fa parte delle ict Analisi delle tetradi
Analisi delle tetradi Analisi non lineare delle strutture
Analisi non lineare delle strutture Analisi delle componenti principali
Analisi delle componenti principali Matrice di burt
Matrice di burt Missa parte por parte slide catequese
Missa parte por parte slide catequese Te invitamos a ser parte o hacer parte
Te invitamos a ser parte o hacer parte Este parte aquele parte
Este parte aquele parte Partes de un decimal
Partes de un decimal Liceo scientifico dolo
Liceo scientifico dolo Vie metaboliche cicliche
Vie metaboliche cicliche Baricentro
Baricentro Legge di stevino generalizzata
Legge di stevino generalizzata Lezioni di fisica giuseppe ruffo
Lezioni di fisica giuseppe ruffo Sovrapposizione delle onde
Sovrapposizione delle onde Galileo galilei dolo
Galileo galilei dolo Accelerazione negativa
Accelerazione negativa Ordine di grandezza
Ordine di grandezza Lezioni partecipate
Lezioni partecipate Liceo montanari.edu.it
Liceo montanari.edu.it Lezioni online unich
Lezioni online unich Fisica: lezioni e problemi 1 soluzioni
Fisica: lezioni e problemi 1 soluzioni