Additive Spanners in Nearly Quadratic Time David Woodruff

Additive Spanners in Nearly Quadratic Time David Woodruff IBM Almaden

Talk Outline 1. Spanners 1. 2. 3. Definition Applications Previous work 2. Our Results 3. Our Techniques for Additive-6 spanner • • 4. New existence proof Efficiency Conclusion

Spanners • G = (V, E) undirected unweighted graph, n vertices, m edges • G (u, v) shortest path length from u to v in G • [A, PS] An (a, b)-spanner of G is a subgraph H such that for all u, v in V, H(u, v) · a G(u, v) + b • If b = 0, H is a multiplicative spanner • If a = 1, H is an additive spanner • Challenge: find sparse H, and do it quickly

Spanner Application • 3 -approximate distance queries G(u, v) with small space • Construct a (3, 0)-spanner H with O(n 3/2) edges. [PS, ADDJS] do this efficiently • Query answer: G(u, v) · H(u, v) · 3 G(u, v) • Algorithmic tool: replace complicated dense graph with spanner – Spanner should be sparse – Algorithm should be efficient

Multiplicative Spanners • [PS, ADDJS] For every k, can find a (2 k -1, 0)-spanner with O(n 1+1/k) edges in O(m) time • This is optimal assuming a girth conjecture of Erdos

Surprise, Surprise • [ACIM, DHZ]: Construct a (1, 2)-spanner H with O(n 3/2) edges in O~(n 2) time • Remarkable: for all u, v: G(u, v) + 2 G(u, v) · H(u, v) · • Query answer is a 3 -approximation, but with much stronger guarantees for G(u, v) large

Additive Spanners • Sparsity Upper Bounds: – (1, 2)-spanner: O(n 3/2) edges [ACIM, DHZ] – (1, 6)-spanner: O(n 4/3) edges [BKMP] – For any constant c > 6, best (1, c)-spanner known is O(n 4/3) – For graphs with few edges on short cycles, can get better bounds [P] • Time Bounds: – A (1, 2)-spanner can be found in O~(n 2) time [DHZ] – A (1, 6)-spanner can be found in O(mn 2/3) time [BKMP, Elkin]

Talk Outline 1. Spanners 1. 2. 3. Definition Applications Previous Work 2. Our Results 3. Our Techniques for Additive-6 spanner • • 4. New existence proof Efficiency Conclusion

Main Contribution • We construct an additive-6 spanner with O~(n 4/3) edges in O~(n 2) time – Improves previous O(mn 2/3) time for all m, n – Based on a new “path-hitting” framework

Corollary: Graphs with Large Girth • We construct additive spanners for input graphs G with large girth in O~(n 2) time • E. g. , if G has girth > 4, we construct an additive 4 -spanner with O~(n 4/3) edges in O~(n 2) time – Improves previous O(mn) time • E. g. , if G has girth > 4, we construct an additive 8 -spanner with O~(n 5/4) edges in O~(n 2) time – Improves previous O(mn 3/4) time • Generalizes to graphs with few edges on short cycles

Corollary: Source-wise Preservers • Given a subset S of O(n 2/3) vertices of G, we compute a subgraph H of O~(n 4/3) edges in O~(n 2) time so that – For all u, v in S, δH(u, v) · δG(u, v) + 2 • Improves previous O(mn 2/3) time

Talk Outline 1. Spanners 1. 2. 3. Definition Applications Previous Work 2. Our Results 3. Our Techniques for Additive-6 spanner • • 4. New existence proof Efficiency Conclusion

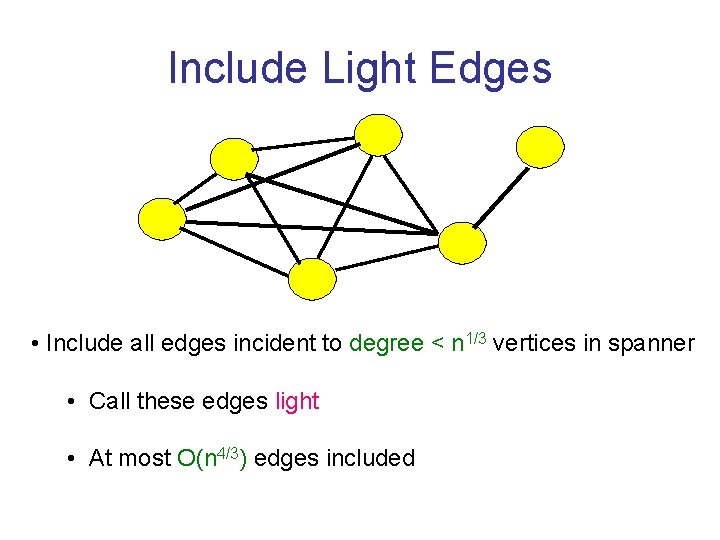
Include Light Edges • Include all edges incident to degree < n 1/3 vertices in spanner • Call these edges light • At most O(n 4/3) edges included

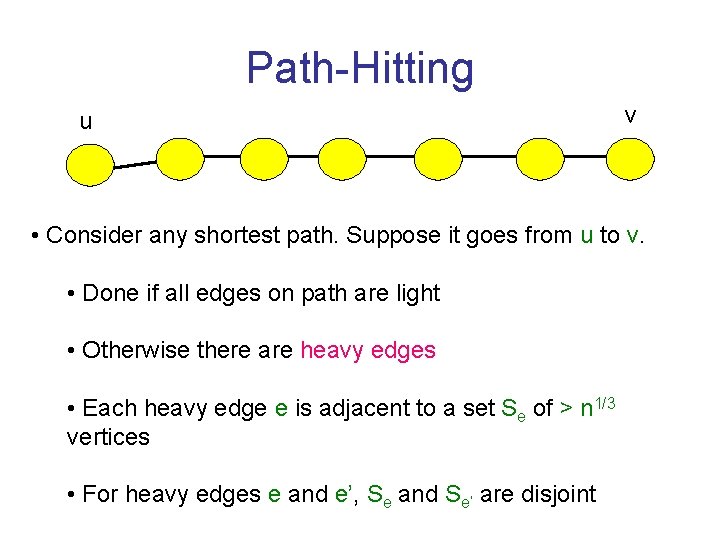
Path-Hitting u v • Consider any shortest path. Suppose it goes from u to v. • Done if all edges on path are light • Otherwise there are heavy edges • Each heavy edge e is adjacent to a set Se of > n 1/3 vertices • For heavy edges e and e’, Se and Se’ are disjoint

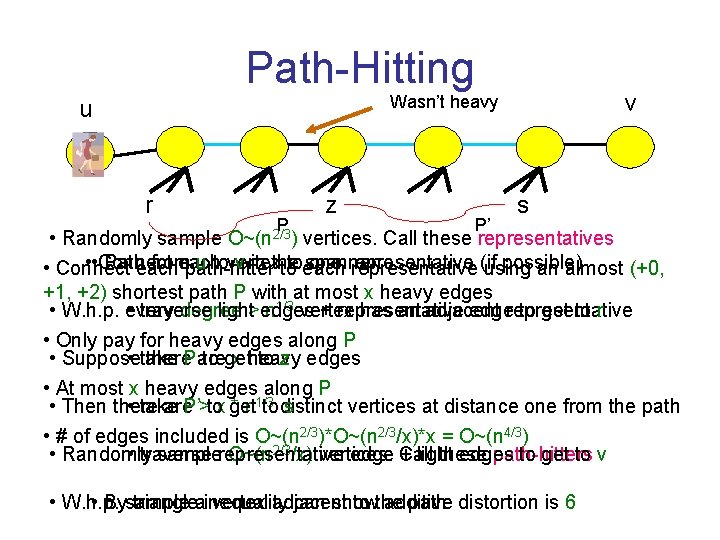
Path-Hitting v Wasn’t heavy u r P z P’ s • Randomly sample vertices. Call these representatives • • Connect Patheach from each u tovertex v in the toeach spanner: one representative possible) • Connect path-hitter to representative (if using an almost (+0, +1, +2) shortest path P with at most x heavy edges • W. h. p. every • traverse degree light> edges n 1/3 vertex + representative has an adjacent edgerepresentative to get to r • Only pay for heavy edges along P • Suppose there. P are x heavy • take to get to z edges • At most x heavy edges along P • Then there • take are. P’>tox get * n 1/3 to distinct s vertices at distance one from the path • # of edges included is O~(n 2/3)*O~(n 2/3/x)*x = O~(n 4/3) • Randomly • traverse samplerepresentative O~(n 2/3/x) vertices. edge Call + light these edges path-hitters to get to v O~(n 2/3) • W. h. p. • Bysample triangleainequality vertex adjacent can show to the additive path distortion is 6

Recap Algorithm: 1. Randomly sample O~(n 2/3) representatives 2. Randomly sample O~(n 2/3/x) path-hitters 3. Connect each representative to each path-hitter on an almost (+0, +1, +2) shortest path using O(x) heavy edges This works w. h. p. for all shortest paths containing between x and 2 x heavy edges To make it work for all shortest paths, vary x in powers of 2 and take the union of the edge-sets Theorem: there exists an additive-6 spanner with O~(n 4/3) edges

Talk Outline 1. Spanners and related objects 1. 2. Definition Applications 2. Previous Work 3. Our Results 4. Our Techniques for Additive-6 spanner • • 5. New existence proof Efficiency Conclusion

Efficiency • Algorithm: 1. Randomly sample O~(n 2/3) representatives 2. Randomly sample O~(n 2/3/x) path-hitters 3. Connect each representative to each path-hitter on an almost (+0, +1, +2) shortest path using O(x) heavy edges • Only one time consuming step • Bicreteria problem: – Almost (+0, +1, +2) shortest path AND O(x) heavy edges • Simple breadth-first-search-like procedure – Time complexity proportional to # of edges in the graph – Only get quadratic time if # of edges is O(n 4/3 x)

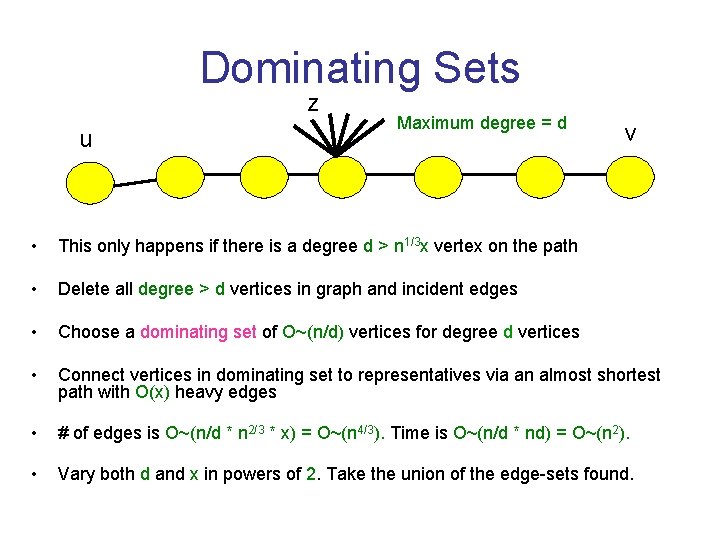
Deleting High Degree Vertices • If maximum degree · n 1/3 x, we get quadratic time • Delete all degree > n 1/3 x vertices and incident edges, run algorithm on subgraph • Oops, some shortest paths are disconnected u v

Dominating Sets z u Maximum degree = d v • This only happens if there is a degree d > n 1/3 x vertex on the path • Delete all degree > d vertices in graph and incident edges • Choose a dominating set of O~(n/d) vertices for degree d vertices • Connect vertices in dominating set to representatives via an almost shortest path with O(x) heavy edges • # of edges is O~(n/d * n 2/3 * x) = O~(n 4/3). Time is O~(n/d * nd) = O~(n 2). • Vary both d and x in powers of 2. Take the union of the edge-sets found.

Talk Outline 1. Spanners and related objects 1. 2. Definition Applications 2. Previous Work 3. Our Results 4. Our Techniques for Additive-6 spanner • • 5. New existence proof Efficiency Conclusion

Conclusion • New path-hitting framework improves running times of spanner problems to O~(n 2) – Additive-6 spanner with O~(n 4/3) edges – Further sparsifies inputs with large girth – Approximate source-wise preservers • Other graph problems for which technique may apply – Constructing emulators more efficiently – Constructing near-additive spanners more efficiently, i. e. , for all pairs u, v, δH(u, v) · (1+ε)δG(u, v) + 4, where ε > 0 is arbitrary