A Szemerdi Regularitsi Lemma kzrtheten Lovsz Lszl Etvs

A Szemerédi Regularitási Lemma (közérthetően? ) Lovász László Eötvös Loránd Tudományegyetem, Budapest lovasz@cs. elte. hu 2012. November 6. 1

Szemerédi Regularitási Lemma Szemerédi Endre 1974 2012. November 6. 2

Szemerédi Regularitási Lemma Szemerédi, E. : On sets of integers containing no four elements in arithmetic progression. Acta Math. Hung. 20 (1969) 89– 104. Szemerédi, E. : On sets of integers containing no k elements in arithmetic progression, Acta Arith. 27 (1975), 199– 245. Ruzsa, I. Z. ; Szemerédi, E. : Triple systems with no six points carrying three triangles. Combinatorics (Proc. 5 th Hung. Colloq. , Keszthely, 1976), 939– 945. Szemerédi, E. : Regular partitions of graphs, Probl. Combin. et Théorie des Graphes, (Colloq. Internat. CNRS, Orsay, 1976); 399 – 401. 2012. November 6. 3

Az Erdős-Turán probléma rk(n) = max(|A|: A {1, . . . , n}, A nem tartalmaz k tagú számtani sorozatot} Erdős-Turán sejtés (1936): minden k-ra, rk(n)/n 0 k=3: Roth 1953 k=4: Szemerédi 1969 k>4: Szemerédi 1975 2012. November 6. 4

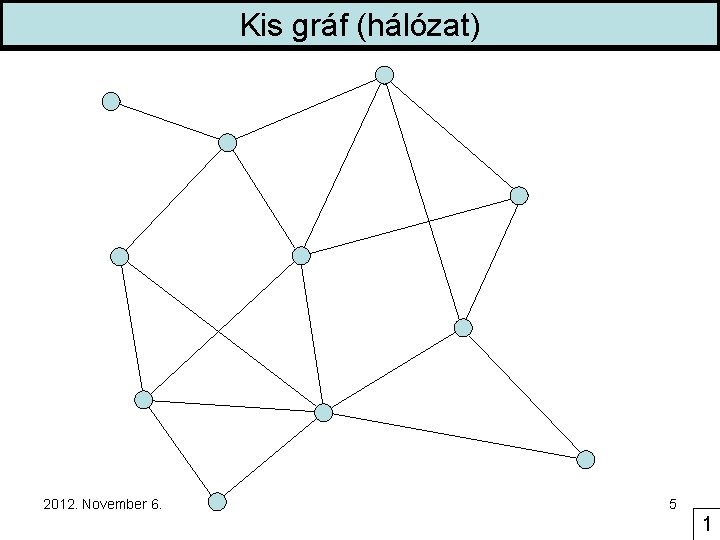
Kis gráf (hálózat) 2012. November 6. 5 1

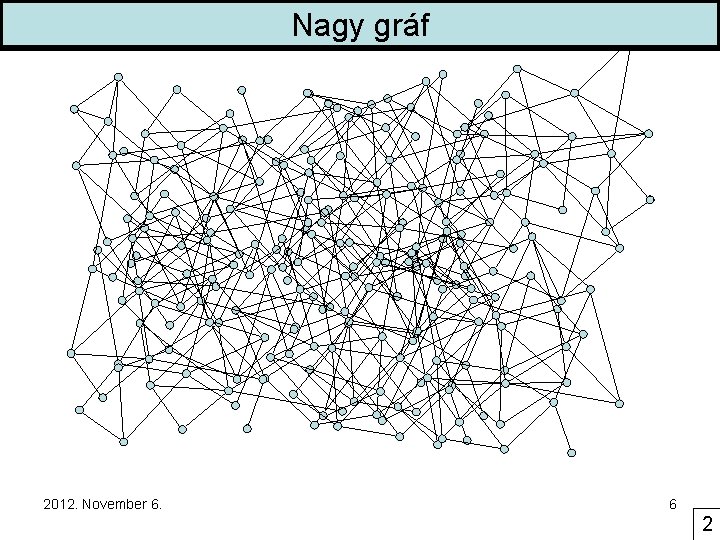
Nagy gráf 2012. November 6. 6 2

Nagyon nagy gráf 2012. November 6. 7 3

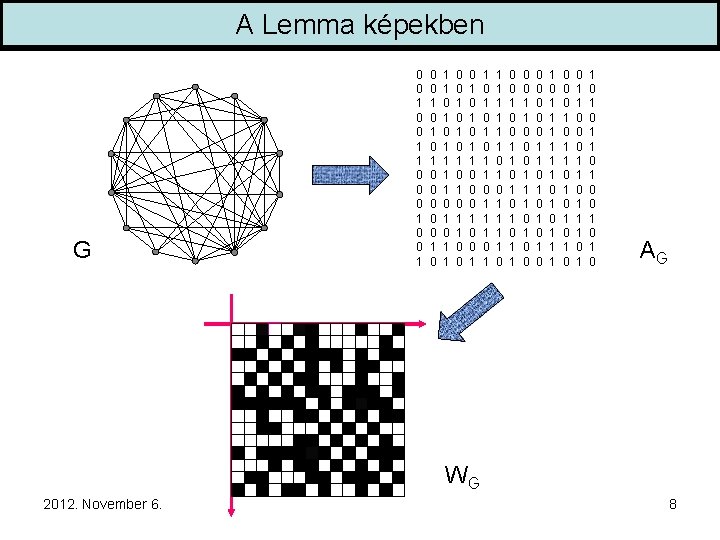
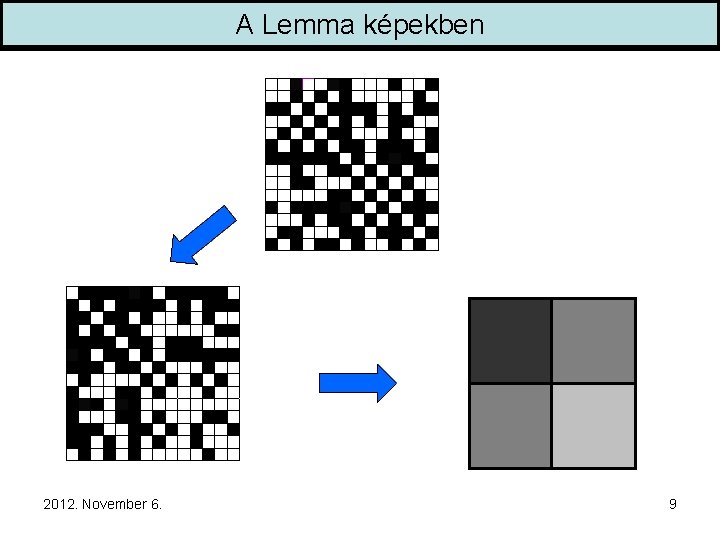
A Lemma képekben G 0 0 1 1 0 0 0 1 0 1 0 0 0 1 0 1 1 1 1 0 0 1 0 1 0 1 1 0 0 0 1 1 0 1 0 1 1 1 1 0 0 0 1 1 0 1 0 1 1 0 0 0 1 1 1 0 0 0 0 1 1 0 1 0 1 0 1 1 1 0 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 1 0 1 0 0 1 0 AG WG 2012. November 6. 8

A Lemma képekben 2012. November 6. 9

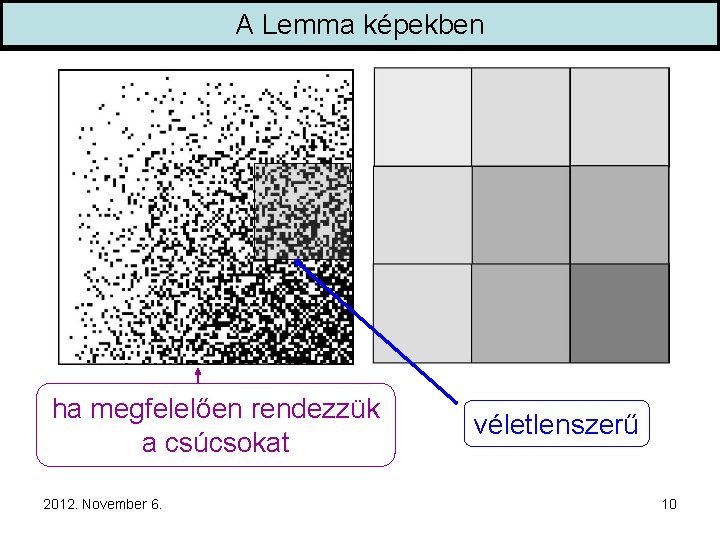
A Lemma képekben ha megfelelően rendezzük a csúcsokat 2012. November 6. véletlenszerű 10

A Lemma Adott >0 Minden gráf csúcsai beoszthatók kevés számú lényegében egyforma osztályba úgy, hogy különbség ≤ 1 a legtöbb osztály-pár közötti páros gráf véletlenszerű ≤ k 2 kivétellel (különböző sűrűséggel). . X Vi, Y Vj 2012. November 6. X és Y közötti élek száma pij|X||Y| ± (n/k)2 11

A Lemma Eredeti Regularitási Lemma Szemerédi 1976 “Gyenge” Regularitási Lemma Frieze-Kannan 1999 “Erős” Regularitási Lemma Alon-Fisher-Krivelevich -M. Szegedy 2000 Tao 2006 L-B. Szegedy 2007 2012. November 6. 12

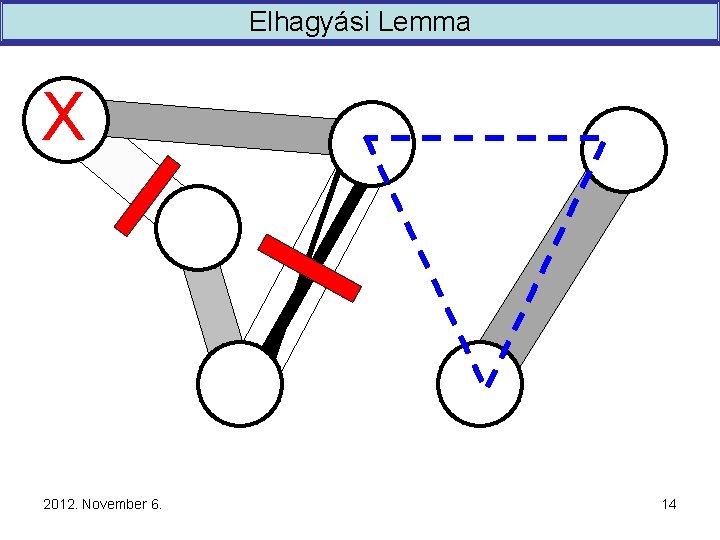
Elhagyási Lemma >0 ’>0 háromszögek száma ’n 3 elhagyható n 2 él úgy, hogy ne maradjon háromszög. Az 1/ ' érték , , csak” log(1/ ) magas torony Ruzsa - Szemerédi Fox 2010 Következményei: Erdős-Turán probléma k=3 esete Háromszögmentesség tesztelhető 2012. November 6. 13

Elhagyási Lemma X 2012. November 6. 14

A Lemma, mint általános séma Nagy, bonyolult struktúra egyszerű struktúra véletlenszerű módosítás (kis) hiba megérthető leirható, kezelhető nagy számok törvénye alkalmazható becsülhető 2012. November 6. 15

A Lemma, mint általános séma Ritka gráfok Kohayakawa, Rödl, Łuczak, Scott, . . . Hipergráfok Frankl, Rödl, Skokan, Schacht, Gowers, . . . Abel-csoportok Green, Tao, Szegedy Permutációk Cooper, Kohayakawa, . . . Boole-függvények Green, Mossel, Schramm, . . . Kategóriák L. . . 2012. November 6. 16

A Lemma más megfogalmazásban - adjacencia-mátrix kis rangú közelítése - 2 -változós függvény közelítése lépcsősfüggvénnyel - sorfejtés Hilbert-térben - gráf-limeszek terének kompaktsága - pontok hasonlóságának (majdnem) véges dimenziója 2012. November 6. 17

A , , gyenge’’ Lemma pij: Vi és Vj közti élsűrűség S S-beli élek száma: 2012. November 6. 18

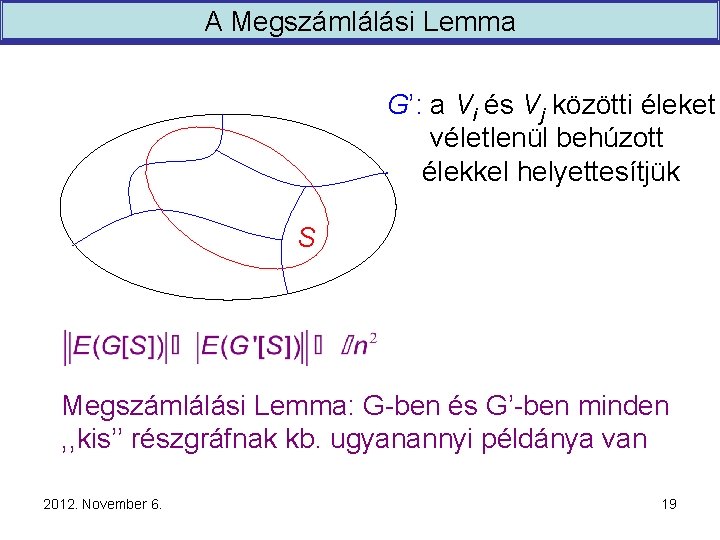
A Megszámlálási Lemma G’: a Vi és Vj közötti éleket véletlenül behúzott élekkel helyettesítjük S Megszámlálási Lemma: G-ben és G’-ben minden , , kis’’ részgráfnak kb. ugyanannyi példánya van 2012. November 6. 19

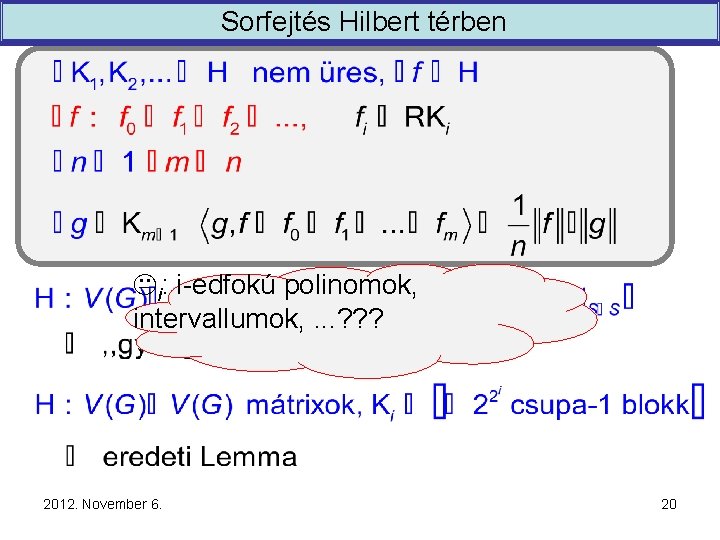
Sorfejtés Hilbert térben Ki: i-edfokú polinomok, intervallumok, . . . ? ? ? 2012. November 6. 20

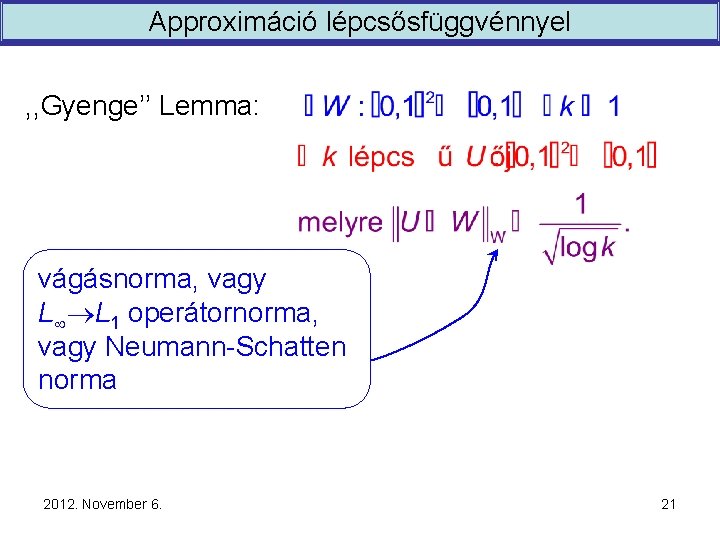
Approximáció lépcsősfüggvénnyel , , Gyenge’’ Lemma: vágásnorma, vagy L L 1 operátornorma, vagy Neumann-Schatten norma 2012. November 6. 21

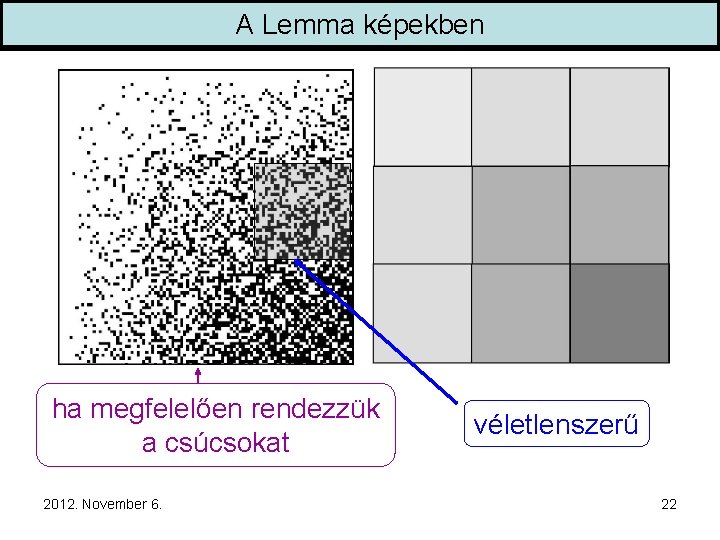
A Lemma képekben ha megfelelően rendezzük a csúcsokat 2012. November 6. véletlenszerű 22

Approximáció lépcsősfüggvénnyel , , Erős’’ Lemma: 2012. November 6. 23

Geometriai változat Hasonlósági távolság: s L-Szegedy B. w u t v Reprezentatív halmaz: s, t U, dsim(s, t) > legtöbb v csúcsra, dsim(U, v) 2012. November 6. 24

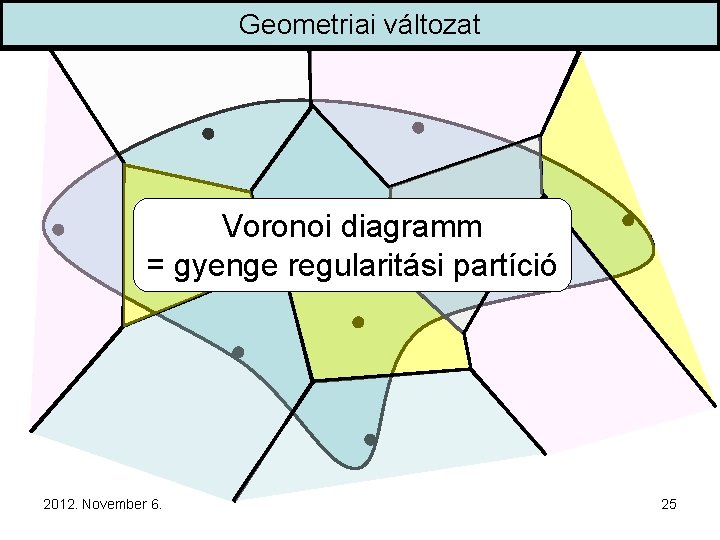
Geometriai változat Voronoi diagramm = gyenge regularitási partíció 2012. November 6. 25

Geometriai változat Minden gráfban van elemű reprezentatív halmaz. Alon A hasonlósági távolságra nézve minden gráf , , majdnem’’ véges dimenziójú. 2012. November 6. 26

Algoritmus A regularitási partíció polinomiális időben kiszámítható. Alon, Duke, Lefmann, Rödl, Yuster 1994 Frieze, Kannan 1999 2012. November 6. 27

Algoritmus Egy reprezentatív halmaz konstans időben kiszámítható. L- Szegedy B. 2012. November 6. 28

És végül. . . 2012. November 6. 29

Analytic version 2. Distance of graphs cut distance (a) V(G) = V(G') (b) |V(G)| = |V(G')| (c) |V(G)| =n, |V(G')|=m (blow up nodes, or fractional overlay) 2012. November 6. 30

Analytic version 2. Distance of graphs “Weak" Regularity Lemma (approximation form): 2012. November 6. 31

Analytic version Graphons W 0 = {W: [0, 1]2 [0, 1], symmetric, measurable} "graphon" t(F, WG) = t(F, G): Probability that random map V(F) V(G) preserves edges 2012. November 6. 32

Analytic version 2. 2012. November 6. Distance of functions 33

Counting Lemma Subgraph densities t(F, G): Probability that random map V(F) V(G) preserves edges (Can be defined for weighted graphs G) |t(F, G) - t(F, H)| |E(F)| □(G, H) If □(G, H) is small, then G and G’ are similar in many other respects. . . 2012. November 6. 34