4 TURUNAN 1 4 1 Konsep Turunan n













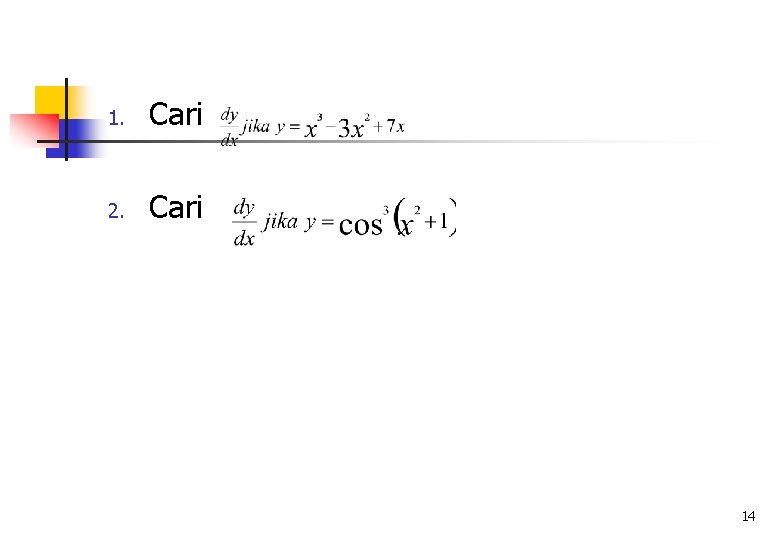


- Slides: 16

4. TURUNAN 1

4. 1 Konsep Turunan n n 4. 1. 1 Turunan di satu titik Definisi 4. 1 Misalkan fungsi f terdefinisi pada selang I yang memuat c. Turunan pertama fungsi f di titik c, ditulis didefinisikan sebagai n Arti geometris: Perhatikan gambar disamping n Kemiringan tali busur PQ adalah : bila limit ini ada. y f ( x) n Q Jika x c , maka tali busur PQ akan berubah menjadi garis singgung di ttk P dgn kemiringan P(c, f (c)) x 2

n n n Jadi, arti geometris dari kurva f di titik (c, f(c)). adalah kemiringan garis singgung Sedangkan arti fisis dari f(x) terhadap peubah x. adalah laju perubahan nilai fungsi Notasi Lain : Contoh Jawab : Diketahui , tentukan 3

4. 1. 2 Turunan Sepihak n Turunan kiri dari fungsi f di titik c, didefinisikan sebagai : n Turunan kanan dari fungsi f di titik c, didefinisikan sebagai : bila limit ini ada. n Fungsi f dikatakan mempunyai turunan ( diferensiabel ) di c atau, ada jika sebaliknya f dikatakan tidak mempunyai turunan di c. 4

Contoh : Diketahui Selidiki apakah f(x) diferensiabel di x=1 Jika ya, tentukan Jawab : a. b. Jadi, f diferensiabel di x=1. 5

n Teorema 4. 1 Jika f diferensiabel di c f kontinu di c. Bukti : Yang perlu ditunjukkan adalah bahwa n Perhatikan bahwa n Maka n = f(c). n Terbukti. Sifat tersebut tidak berlaku sebaliknya. Artinya, Jika f kontinu di c, maka belum tentu f diferensiabel di c. Hal ini, ditunjukkan oleh contoh berikut. 6

4. 2 Aturan Pencarian Turunan n Fungsi Turunan Pertama Definisi 4. 3 Misalkan f (x) terdefinisi pada selang I. Fungsi turunan pertama dari f, ditulis , didefinisikan sebagai n atau jika h=t-x bila limitnya ada. n Notasi lain , bentuk dikenal sebagai notasi Leibniz. 7

n Dengan menggunakan definisi tersebut dapat diturunkan aturan untuk mencari turunan sebagai berikut : n 1. Jika f (x)=k, maka n 2. n 3. n 4. n 5. dengan g(x) 0. Contoh Tentukan fungsi turunan pertama dari Jawab: 8

n Carilah turunan nya 1. 2. 3. jari-jari sebuah semangka bulat tumbuh dg laju tetap sebesar 2 cm/minggu. Ketebalan kulitnya selalu sepersepuluh jari-jarinya. Seberapa cepat isi kulit berkembang pada akhir minggu kelima? Anggap jari-jari semula nol 9

n 4. 3 Turunan Fungsi Sinus dan Cosinus n Turunan fungsi trigonometri yang lain : n 1. 2. n 3. 4. n Contoh: Tentukan dari 10

4. 4 Aturan Rantai n n n Andaikan y = f(u) dan u = g(x). Jika maka dan ada , Jika y = f (u ) , u = g(v), dan v = h(x) maka : Contoh: Jika Tentukan Jawab: 11

Carilah turunan dari 1. 2. 3. 12

4. 5 Notasi leibniz n Notasi lain dikenal , bentuk sebagai notasi Leibniz. 13
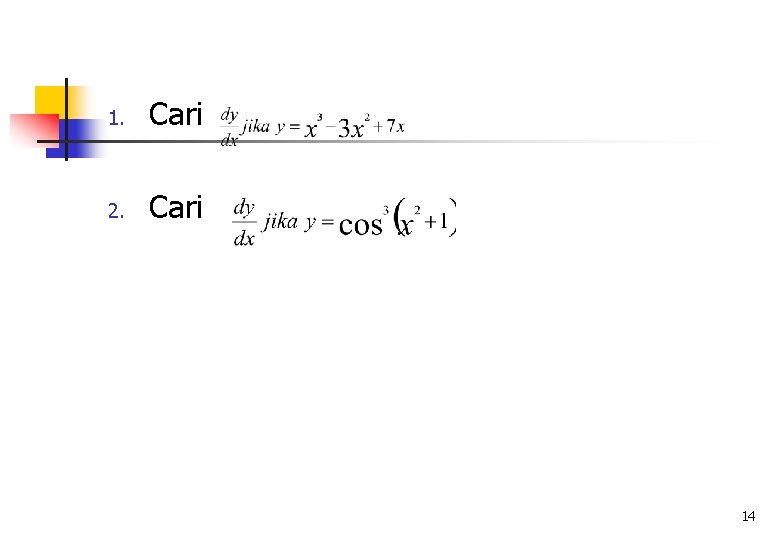
1. Cari 2. Cari 14

4. 5 Turunan Tingkat Tinggi n Turunan ke-n didapatkan dari penurunan turunan ke-(n-1). n Turunan pertama n Turunan kedua n Turunan ketiga n Turunan ke-n n Contoh : Tentukan n Jawab : dari , maka 15

4. 6 Turunan Fungsi Implisit n n Jika hubungan antara y dan x dapat dituliskan dalam bentuk y = f(x) maka y disebut fungsi eksplisit dari x, yaitu antara peubah bebas dan tak bebasnya dituliskan dalam ruas yang berbeda. Bila tidak demikian maka dikatakan y fungsi implisit dari x. Untuk menentukan turunan dari bentuk implisit digunakan aturan rantai dan anggap y fungsi dari x. Contoh: Tentukan y’ dari bentuk implisit Sin(xy) = x 2 + 1 Jawab: Dx (Sinxy) = Dx(x 2 + 1) Cos(xy) Dx(xy) = 2 x Cos(xy) (y + x ) = 2 x Maka 16
 Materi turunan parsial
Materi turunan parsial Bab 1 besaran dan pengukuran
Bab 1 besaran dan pengukuran Peta konsep turunan fungsi
Peta konsep turunan fungsi Peta konsep kerja sama ekonomi internasional
Peta konsep kerja sama ekonomi internasional Metode kualitatif dalam perencanaan sdm
Metode kualitatif dalam perencanaan sdm Contoh perilaku husnuzan terhadap sesama adalah
Contoh perilaku husnuzan terhadap sesama adalah Pembuatan konsep persetujuan konsep pengetikan
Pembuatan konsep persetujuan konsep pengetikan Pengertian profesi keguruan
Pengertian profesi keguruan Maksud konsep merekayasa
Maksud konsep merekayasa Konsep dasar komunikasi
Konsep dasar komunikasi Konsep konsep penelitian ilmiah
Konsep konsep penelitian ilmiah Sekumpulan konsep konsep untuk menerangkan data
Sekumpulan konsep konsep untuk menerangkan data Simbol garis atau line pada er model adalah menunjukan
Simbol garis atau line pada er model adalah menunjukan Konsep dasar wirausaha
Konsep dasar wirausaha Perbedaan fbm dan abm
Perbedaan fbm dan abm Pengertian ruang lingkup pendidikan seni
Pengertian ruang lingkup pendidikan seni Lambang besaran panjang
Lambang besaran panjang