308 203 A Introduction to Computing II Lecture

308 -203 A Introduction to Computing II Lecture 9: Binary Search/Trees Fall Session 2000

Binary Search • Goal: Find a particular element in a sorted array • Solution: Break the data to be searched in two by looking at the middle element • Example: Looking up a word in the dictionary one usually starts by opening the dictionary near the middle

Binary Search: example Lookup “ 20” in a sorted array of 16 elements: (1, 4, 12, 15, 17, 20, 33, 41, 49, 57, 72, 88, 92, 94, 102, 145) Middle (8 th) element = 41 > 20

Binary Search: example Lookup “ 20” in a sorted array of 16 elements: Remaining 7 elements (1, 4, 12, 15, 17, 20, 33, 41, 49, 57, 72, 88, 92, 94, 102, 145) Middle (4 th) element = 15 < 20

Binary Search: example Lookup “ 20” in a sorted array of 16 elements: Remaining 3 elements (1, 4, 12, 15, 17, 20, 33, 41, 49, 57, 72, 88, 92, 94, 102, 145) Middle (6 th) element = 20 done

Pseudocode (recursive) Find( x, A[min. . max] ) { middle = A[min + (max - min)/2 ] ; if (middle = x) return A[ middle ] ; else if (middle < x) return Find(x, A[min, middle-1] else return Find(x, A[middle+1, max]); }

Recurrence Equation Worst case: we don’t find x until only one element is left to check The recurrence: The solution: T(1) = 1 T(n) = 1 + T(n/2) = 1 + (1 + T(n/4) ) = 1 + … + T(n/2 i) + … T(1) = O( log n )

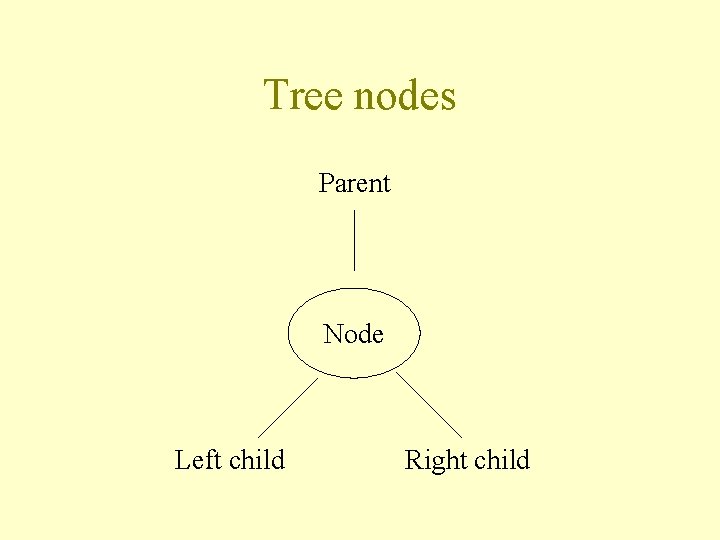
Trees Definition: A tree is a collection of nodes where each node may have: a) one parent-node b) one left child-node c) one right child-node There is exactly one node in the tree which has no parent, and it is called the root. All other nodes have exactly one parent

Tree nodes Parent Node Left child Right child

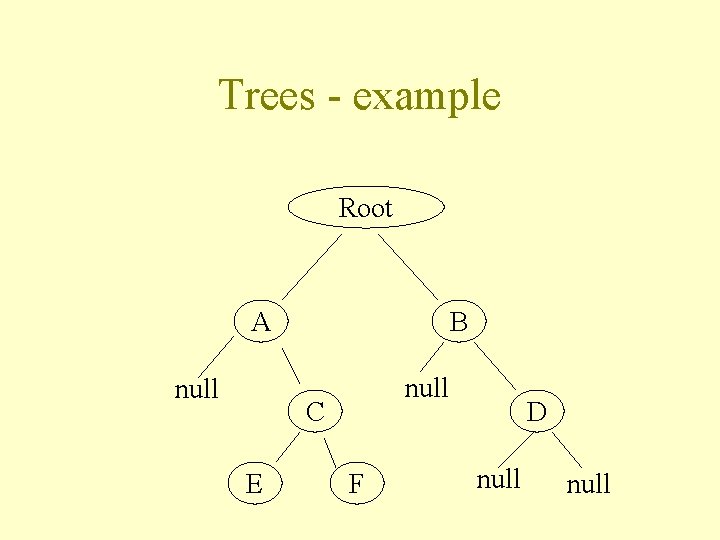
Trees - example Root A null B null C E F D null

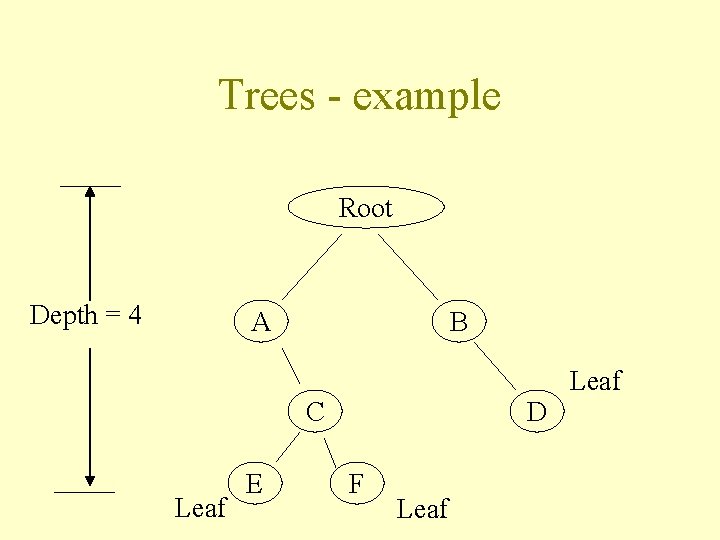
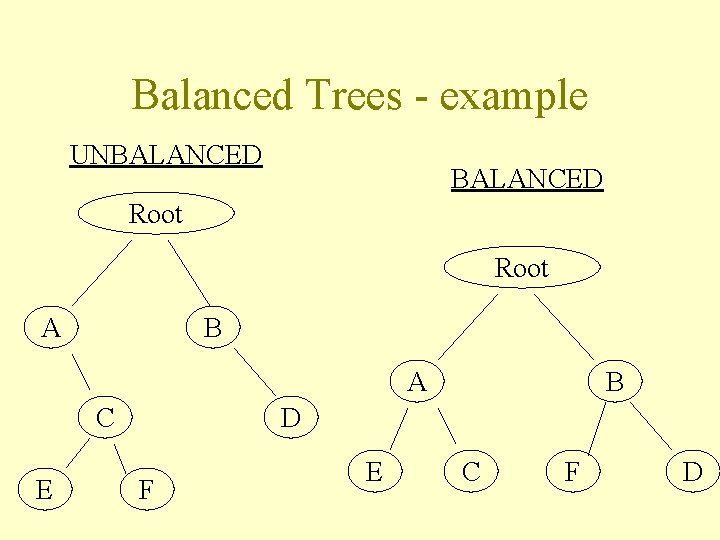
Definitions Definition: A leaf of a tree is an node with no children Definition: The depth of the tree is the length of the longest path from root to leaf Definition: A balanced tree is a tree where the depth is O( log n ), n being the number of nodes in the tree

Trees - example Root Depth = 4 A B Leaf C Leaf E D F Leaf

Balanced Trees - example UNBALANCED Root A B A C E B D F E C F D

Binary Search Trees We can store data in a tree in an order corresponding to a binary search 15 4 1 20 12 41 17 33

Binary Search Trees Definition: A binary search tree is a tree in which where nodes have the binary search property: I. For any node Y reached through the left child of a node X, Y < X II. For any node Y reached through the right child of a node X, X < Y

Tree Traversal traversal - Visiting all nodes in a tree This can be done in three different ways: • preorder traversal • inorder traversal • postorder traversal

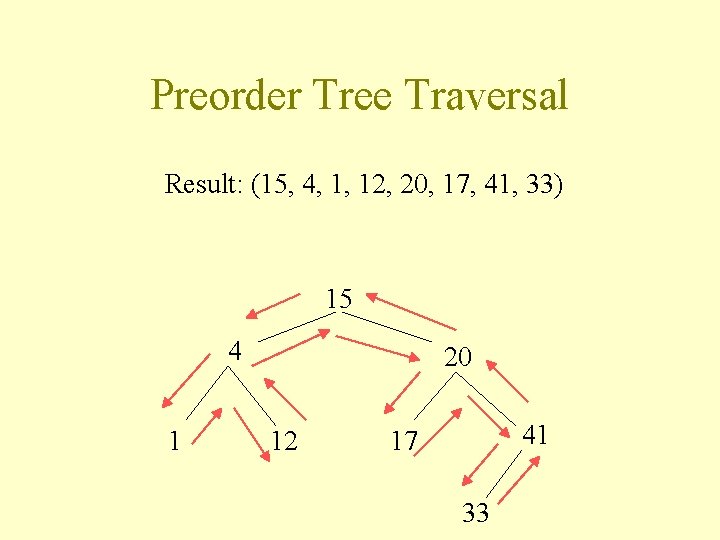
Preorder Tree Traversal Preorder( node N ) { // Do something with N first print(N. key); // Visit the children preorder(N. left. Child); preorder(N. right. Child); }

Preorder Tree Traversal Result: (15, 4, 1, 12, 20, 17, 41, 33) 15 4 1 20 12 41 17 33

Postorder Tree Traversal Postorder( node N ) { // Visit the children postorder(N. left. Child); postorder(N. right. Child); // Do something with N afterwards print(N. key); }

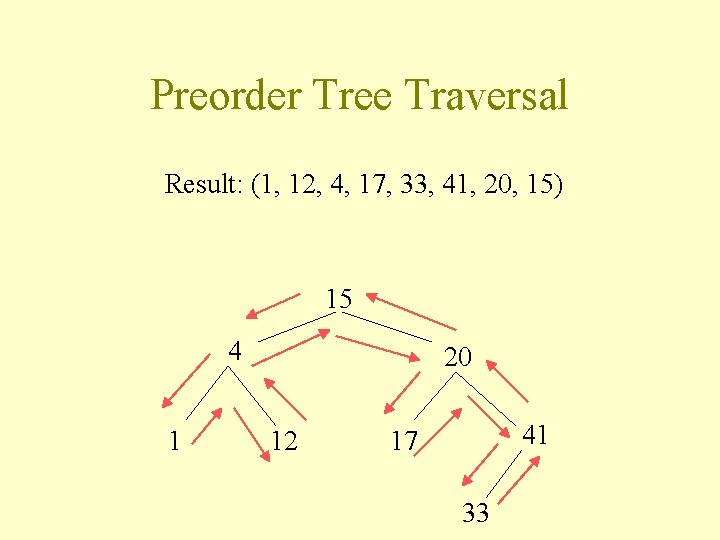
Preorder Tree Traversal Result: (1, 12, 4, 17, 33, 41, 20, 15) 15 4 1 20 12 41 17 33

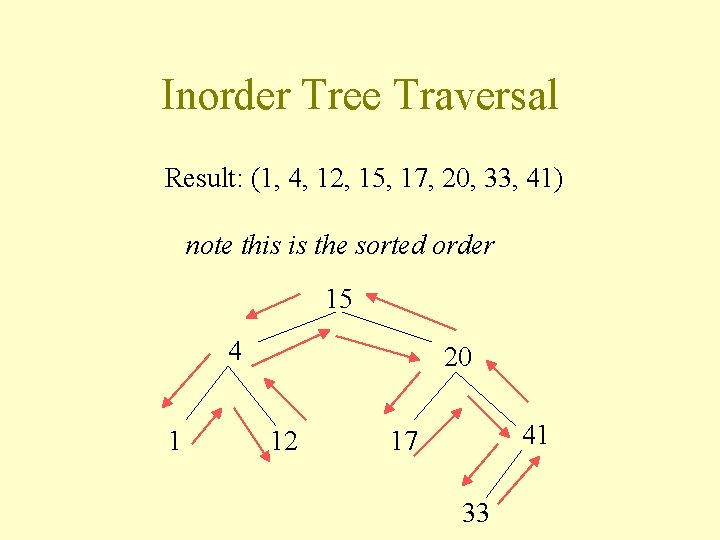
Inorder Tree Traversal Inorder( node N ) { // Visit the left children inorder(N. left. Child); // Do something with N print(N. key); // Visit the rightchildren inorder(N. right. Child); }

Inorder Tree Traversal Result: (1, 4, 12, 15, 17, 20, 33, 41) note this is the sorted order 15 4 1 20 12 41 17 33

Order of Growth O( n ) because we visit each node exactly once and at each node do Q( 1 ) computations

Search To search, start from the root and follow the appropriate child links. Search( Key x, Node N ) { if (N. key = x) done; if (x < N. key) Search(x, N. left. Child); else Search(x, N. left. Child); }

Order of Growth? O( d ) where d is the depth of the tree What is that in terms of n? ? ?

Order of Growth? O( d ) where d is the depth of the tree What is that in terms of n? ? ? log n < d < n depending on whether the tree is balanced

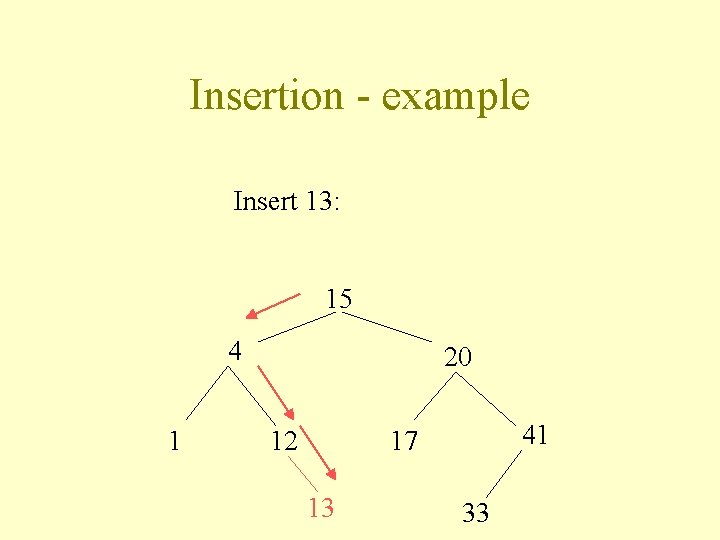
Insertion of a new node A simple algorithm: I) Do “Search” until you find where the node belongs II) Insert it there

Insertion - example Insert 13: 15 4 1 20 12 41 17 13 33

Insertion - Like search takes O( d ) time - Does not guarantee the tree will be balanced - For this reason there are specialized “balanced tree” algorithms which preserve balance, e. g. AVL trees, Red-Black trees, etc.

Any questions?