308 203 A Introduction to Computing II Lecture

308 -203 A Introduction to Computing II Lecture 15: Searching Graphs II Fall Session 2000

Depth-First Search (Assume all nodes start off colored white) DFS-Visit(Vertex v) { v. set. Color(grey); for each u in v. neighbors() if (u. color( ) == white) DFS-Visit(u); v. set. Color(black); }

Running Time of DFS For a connected graph G= (V, E), DFS-Visit will be called exactly once per vertex. When called for a vertex v V, the time taken is: Tv = time for the “for” loop + constants = ( degree(v) ) + (1)

Running Time of DFS Total Time = v V [ Tv ] [ degree(v) + 1 ] = v V degree(v) + = O( |E| + |V| ) v V 1

Deficiencies of DFS explores a single path until it hits a cycle and then backtracks… this was observed to be stupid for some examples, like graphs representing games. What if we take the other extreme and always fully explore the nth step before considering possible steps for (n+1)?

Breadth-First Search (BFS) • Maintain a queue of vertices to explore • Service the queue by exploring that vertex • When exploring a vertex, queue up any unexplored neighbors

Breadth-First Search Again, assume all vertices start of “white” BFS( Vertex start. Vertex ) { start. Vertex. set. Color(grey); queue. enqueue( start. Vertex ); while (queue. has. More. Elements( )) { Vertex v = queue. dequeue( ); explore( v ); } }

Breadth-First Search explore( Vertex v ) { forall u Neighbors( v ) if (u. color() == white) { u. set. Color( grey ) ; queue. enqueue( u ); } v. set. Color( black ); }

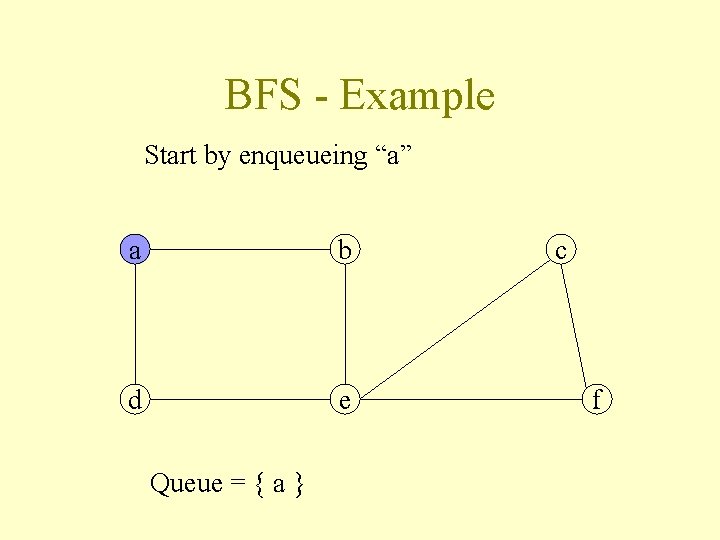
BFS - Example Start by enqueueing “a” a b d e Queue = { a } c f

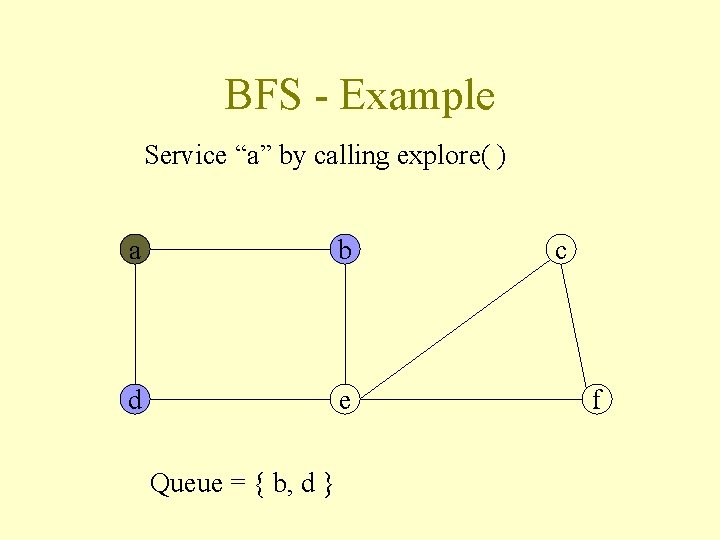
BFS - Example Service “a” by calling explore( ) a b d e Queue = { b, d } c f

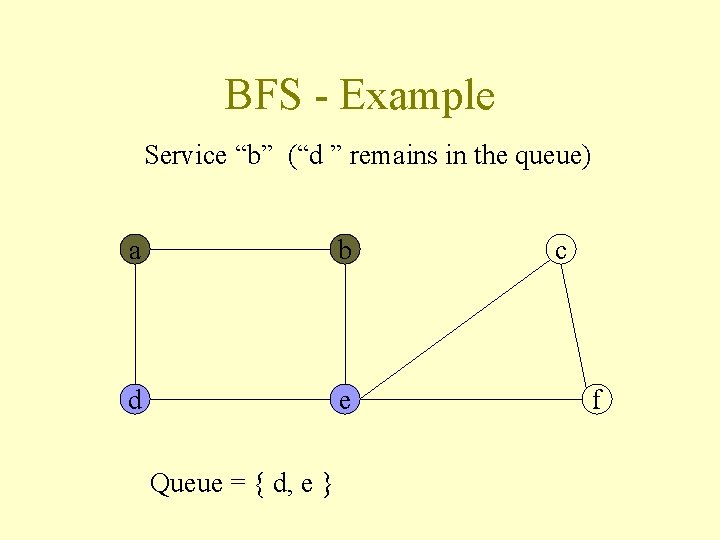
BFS - Example Service “b” (“d ” remains in the queue) a b d e Queue = { d, e } c f

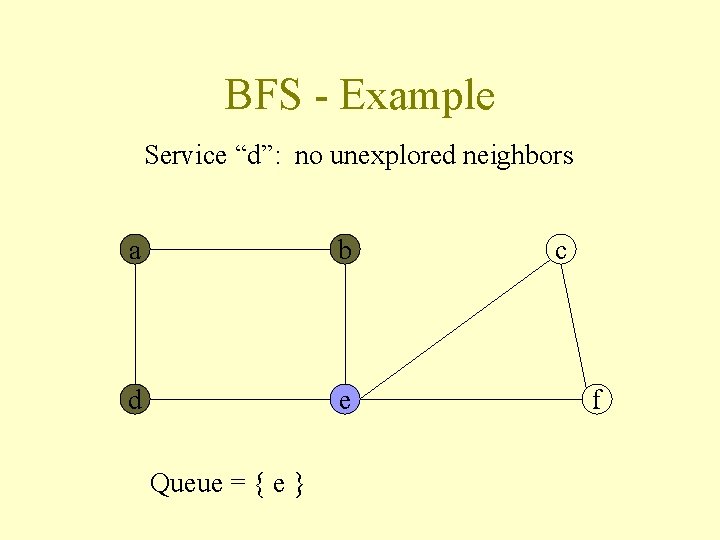
BFS - Example Service “d”: no unexplored neighbors a b d e Queue = { e } c f

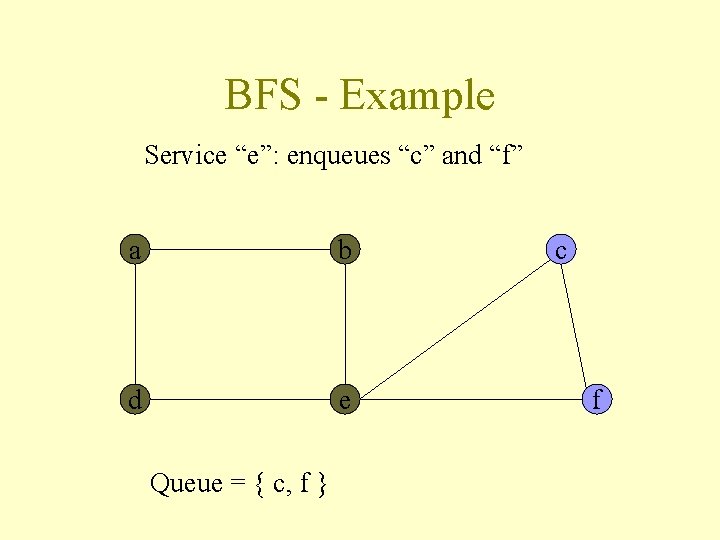
BFS - Example Service “e”: enqueues “c” and “f” a b d e Queue = { c, f } c f

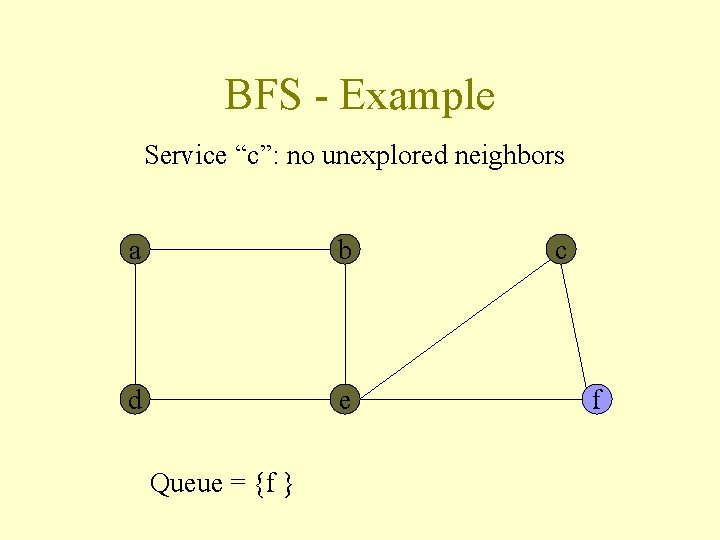
BFS - Example Service “c”: no unexplored neighbors a b d e Queue = {f } c f

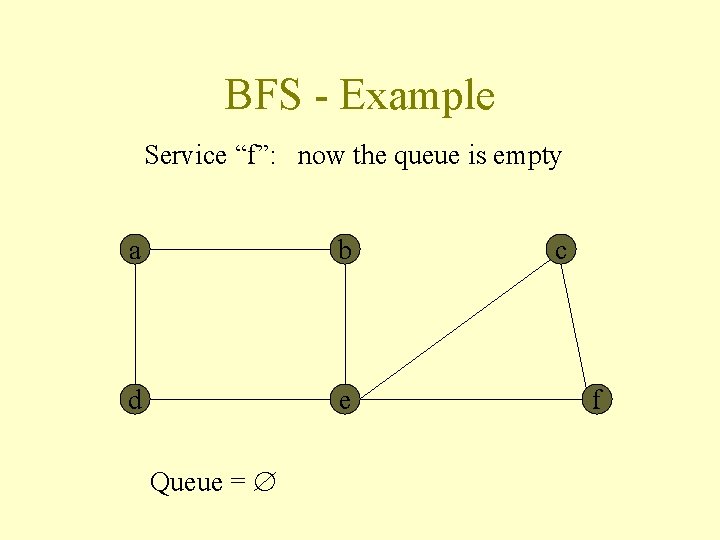
BFS - Example Service “f”: now the queue is empty a b d e Queue = c f

BFS and trees • Like DFS this can be thought of as inducing a tree (with edges from any node u to each other node v which it enqueues)

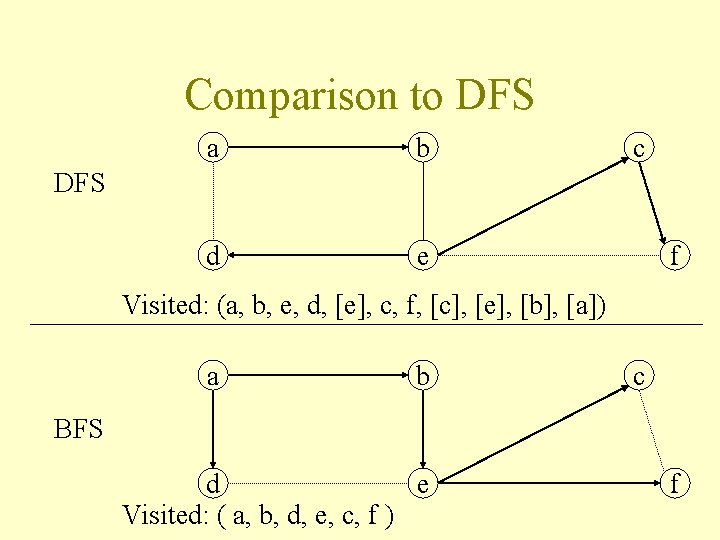
Comparison to DFS a b d e c DFS f Visited: (a, b, e, d, [e], c, f, [c], [e], [b], [a]) a b c BFS d e Visited: ( a, b, d, e, c, f ) f

Running time of BFS? Same as for DFS: for exactly the same reason! • Every node gets enqueued, and therefore explored exactly once • In explore, there is a loop over all adjacent vertices, giving the same O( degree(v) ) term O( |V| + |E| )

Any questions?