308 203 A Introduction to Computing II Lecture

308 -203 A Introduction to Computing II Lecture 13: Trees Fall Session 2000

Trees as graphs We’ve already seen particular examples of trees, aka: • Binary search trees • Call trees of recursive functions (e. g. Merge-sort) • Heaps More generally trees are a special kind of graphs…

Definition: A Forest is an undirected, acyclic graph

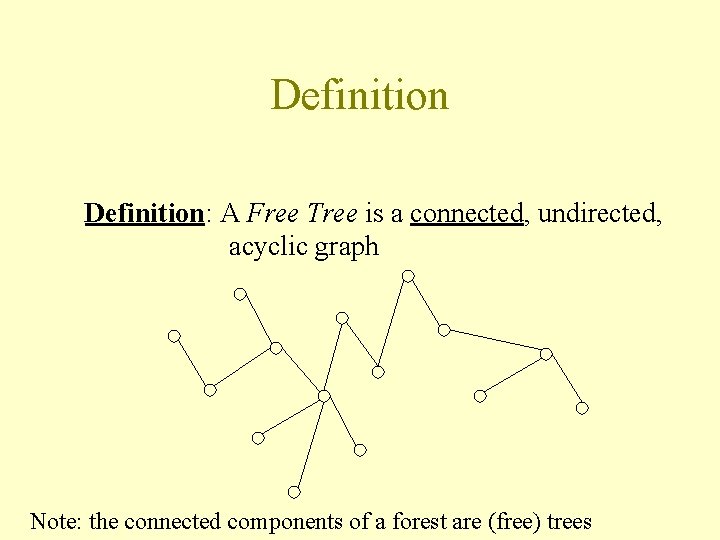
Definition: A Free Tree is a connected, undirected, acyclic graph Note: the connected components of a forest are (free) trees

Is this really what we’ve seen before as trees? We have not (yet) made any distinction of “parent” or “child” vertices. Topologically, the structure has the same important properties, as we will see presently. . .

Defining Characteristics The following statements are equivalent: 1. G = (V, E) is a (free) tree 2. Any two vertices v 0 and v 1 in V are connected by a unique, simple path 3. G is singly-connected (removing any edge disconnects the graph) More on next slide…

Defining Characteristics The following statements are equivalent: 4. G is connected and |E| = |V| -1 5. G is acyclic and |E| = |V| -1 6. G is acyclic but the addition of any edge will create a cycle More on previous slide…

Proof We prove the following sequence of the above facts: 1 2 3 4 5 6 1 This means any one of these six assertions proves all the others.

Any questions?

Rooted Trees For a tree G = (V, E), pick any vertex v in V and call it the “root. ” All v’s neighbors are considered “children” of v. In this way, we can define a parent-child relationship for neighboring nodes in G.

Rooted Trees You can think of “rooting” a tree in terms of the following recursive pseudocode: Root. Tree(Vertex v) { for u neighbors(v) { parent(v) = u if v parent(u), child(u) = child(u) v Root. Tree(u) } }

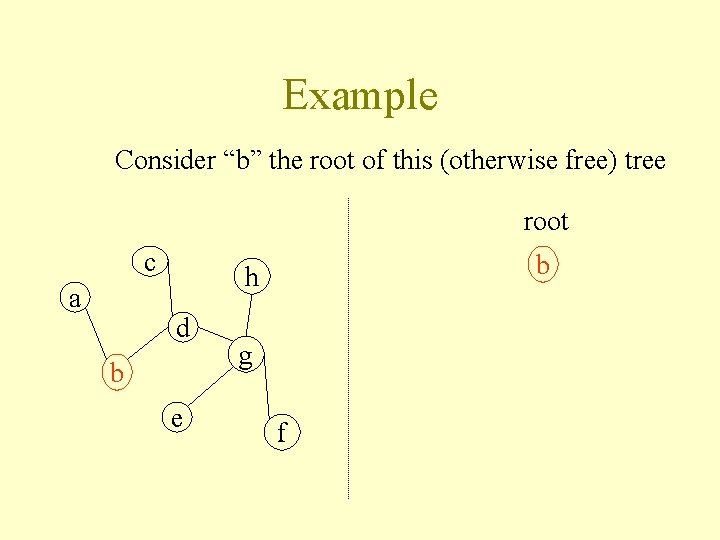
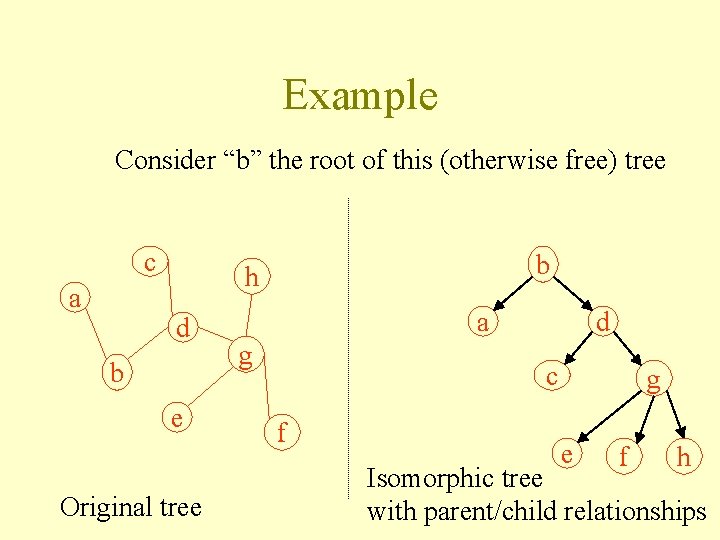
Example Consider “b” the root of this (otherwise free) tree root c a b h d b e g f

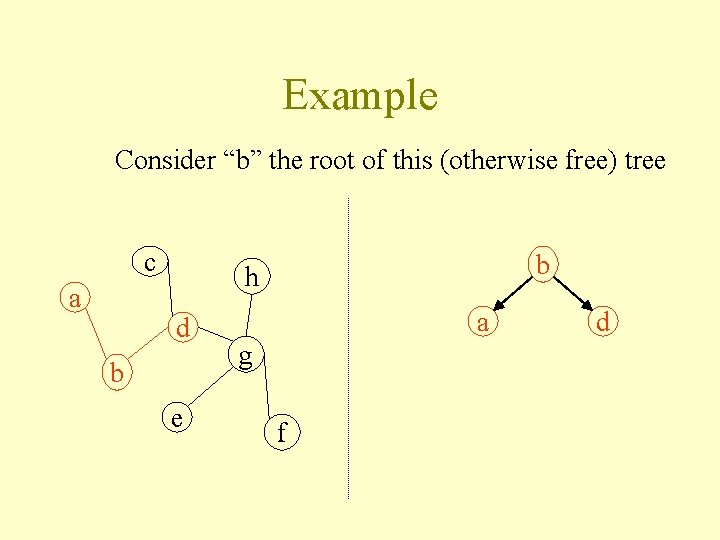
Example Consider “b” the root of this (otherwise free) tree c a b h d b e a g f d

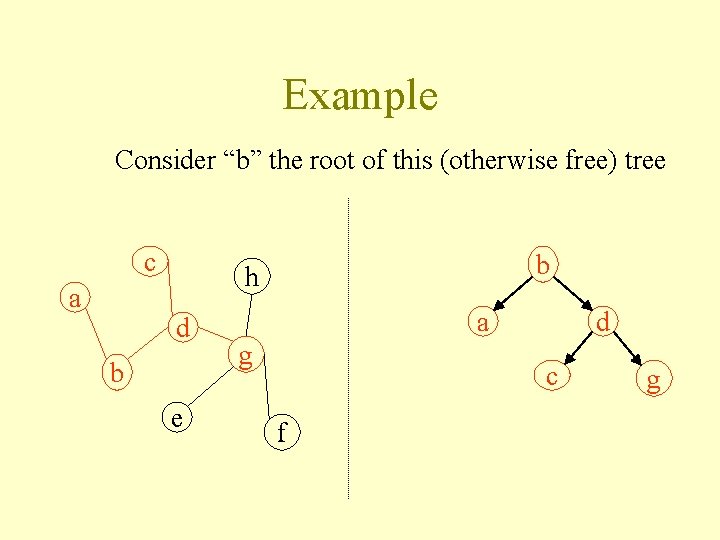
Example Consider “b” the root of this (otherwise free) tree c a b h d b e a g d c f g

Example Consider “b” the root of this (otherwise free) tree c a b h d b e Original tree a g d c f g e f h Isomorphic tree with parent/child relationships

K-ary trees Definition: A rooted tree for which every vertex has at most k children is called a k-ary tree. Definition: In particular, a k-ary tree in which every vertex has at most 2 children is called binary tree. Definition: A k-ary tree in which every vertex has exactly k children is called a complete k-ary tree.

Facts For a complete k-ary tree with of depth d: • There are k i nodes at depth i • There are n = (k d - 1)/(k-1) nodes Conversely, for a complete k-ary tree of n nodes, the depth is d = logk [ n (k-1) + 1] = O( log n)

Any questions?