2 3 Calculating Limits Using the Limit Laws


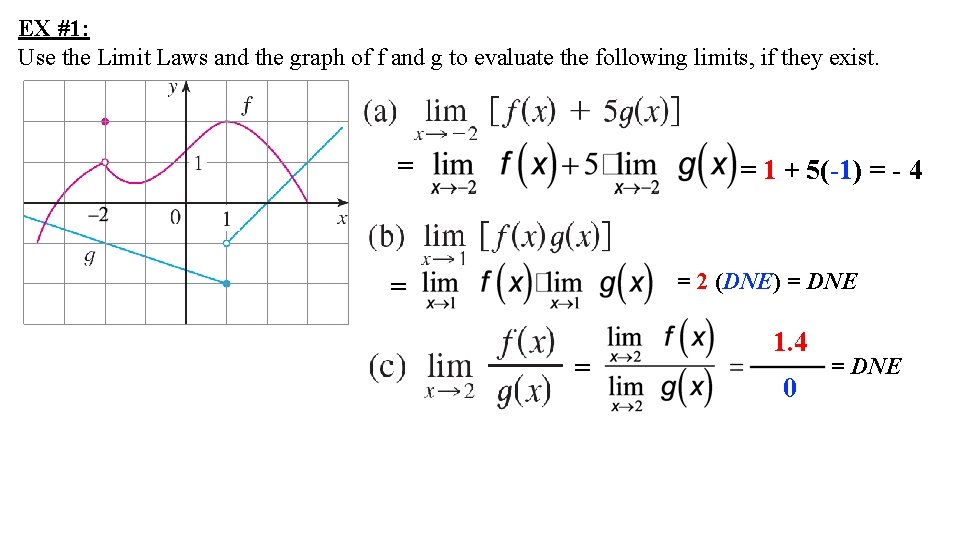

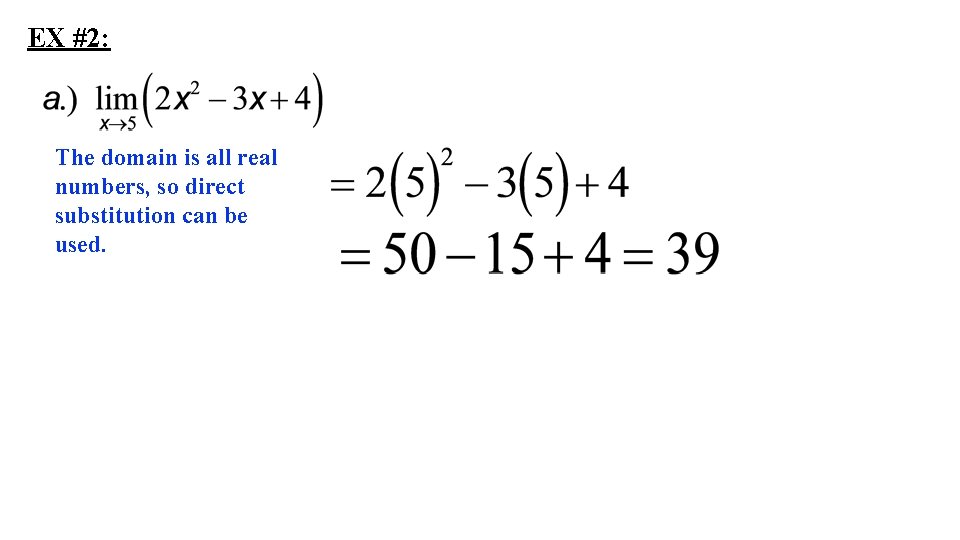
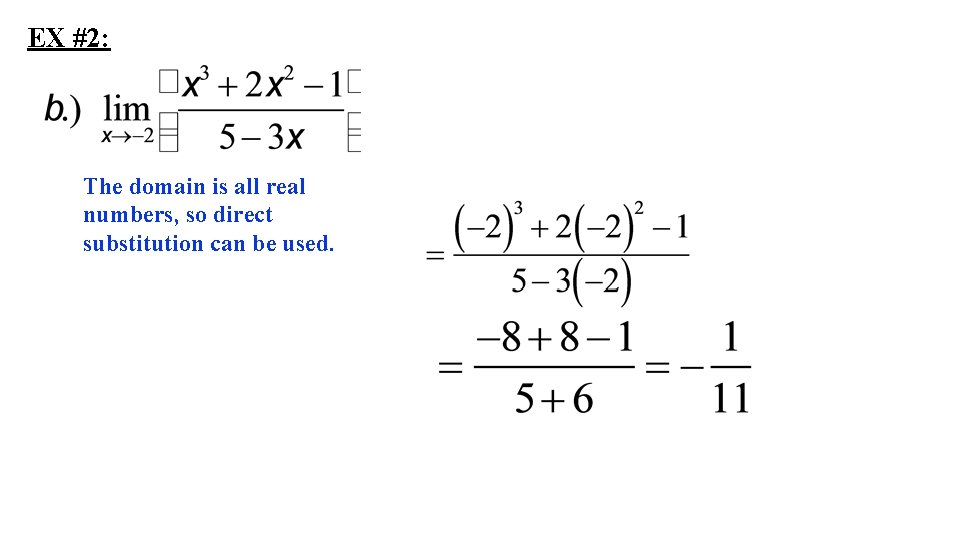








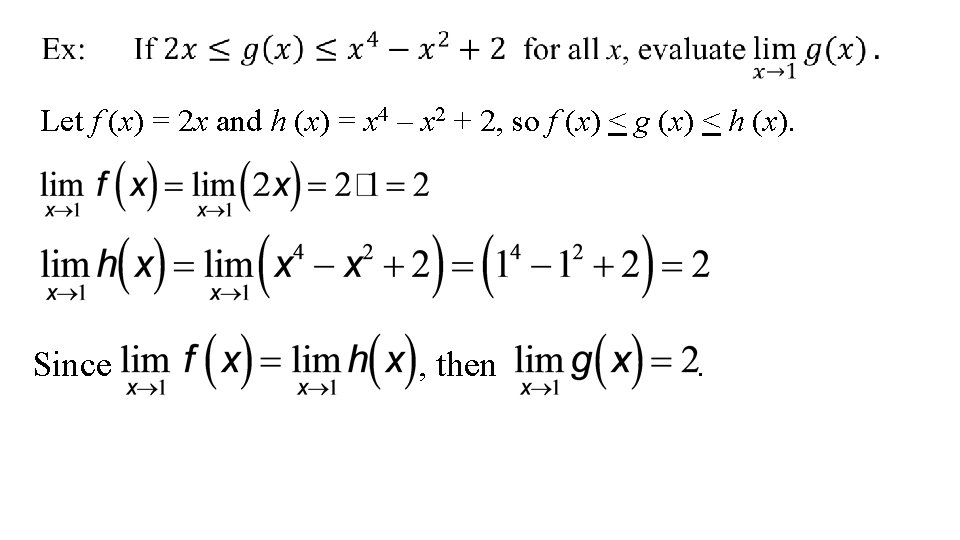



- Slides: 20

2. 3 Calculating Limits Using the Limit Laws: In section 2. 2 we used graphs and tables of values to determine the values of limits. In this section, we use properties of limits to calculate limits analytically. Direct Substitution: Substitute the value that x approaches into the function. 3 -4 4 Basic Limits: b c cn

1. The limit of a sum is the sum of the limits. 2. The limit of a difference is the difference of the limits. 3. The limit of a constant times a function is the constant times the limit of the function. 4. The limit of a product is the product of the limits. 5. The limit of a quotient is the quotient of the limits, provided the limit of the denominator is not 0.
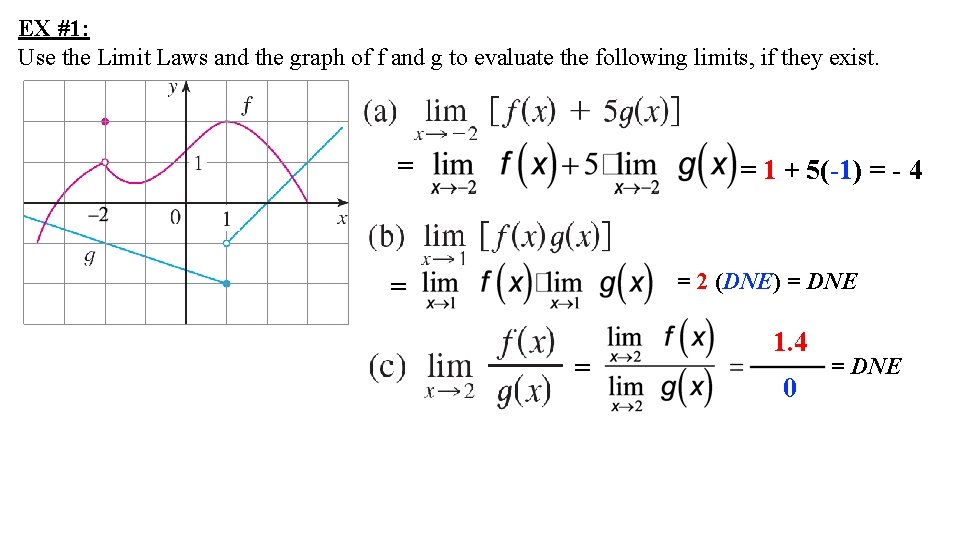
EX #1: Use the Limit Laws and the graph of f and g to evaluate the following limits, if they exist. = = 1 + 5(-1) = - 4 = 2 (DNE) = DNE = = 1. 4 0 = DNE

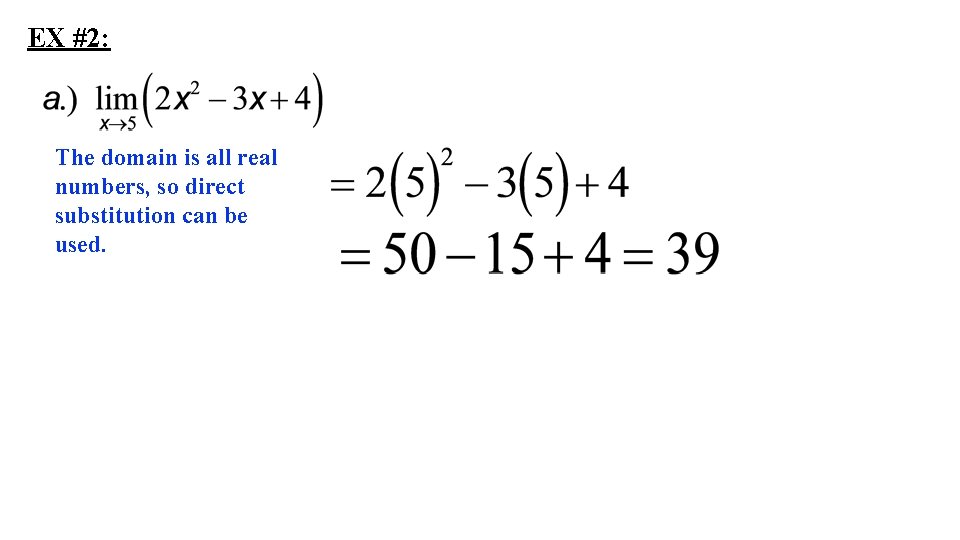
EX #2: The domain is all real numbers, so direct substitution can be used.
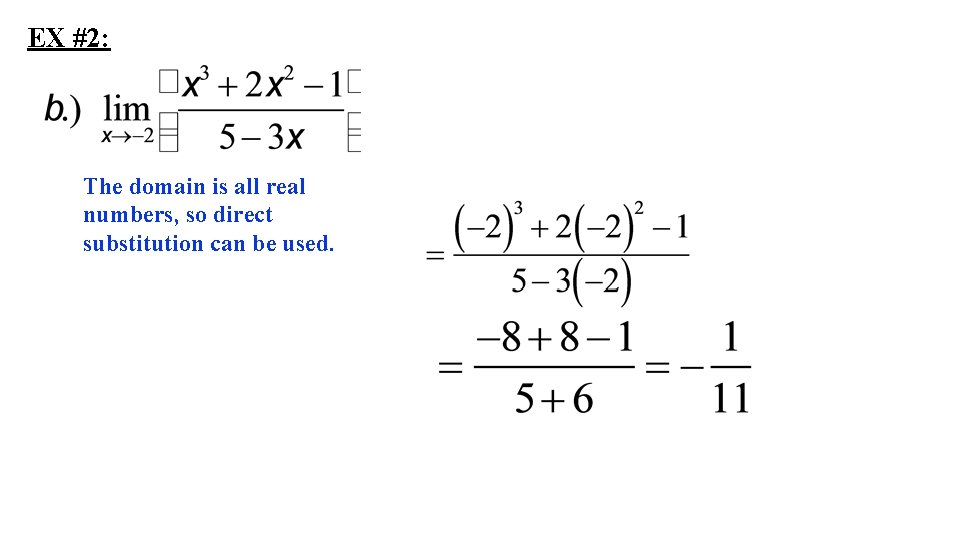
EX #2: The domain is all real numbers, so direct substitution can be used.

When using substitution… * if ____occurs, the limit DOES exist try _________ simplifying re-substituting. and __________ Methods of Simplifying: 1. Factoring 2. Rationalizing * if _____occurs, the limit DOES NOT exist (vertical asymptote at x = c)

What if there is no canceling after you factor? When the numerator and denominator both approach zero, the limit may be finite or infinite value.

Double check. EX #3: DNE Substitution gives us 1 a. Left of 1, 0. 9 (0. 9)3 +1, Positive. 1 a. Right of 1, 1. 1 (1. 1)3 +1, Positive. 2 a. Left of 1, 0. 9 (0. 9) – 1, Negative 2 b. Right of 0, 0. 1 (1. 1) – 1, Positive.

EX #5: substitution: try simplifying numerator:

EX #6: substitution: Multiply by the conjugate. try simplifying numerator:

Recall that Right side. Since | x | = x for x > 0, we have Left side. . For x < 0, we have | x | = – x , so Therefore, by Theorem 1, . .

Using previous facts that | x | = x for x > 0 and | x | = – x we have for x < 0, We can make the following changes… Right side. Left side. Since the left and right sides are different, it follows from Theorem 1 that the limit does not exist.

EX #9: If determine whether exists. Right side. Left side. Since the left and right sides are equal, a limit does exist and .

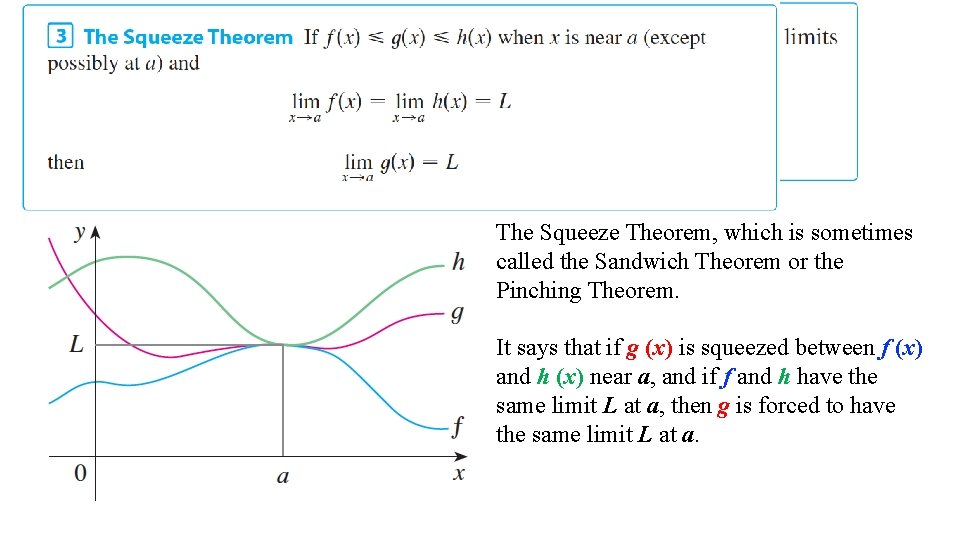
The Squeeze Theorem, which is sometimes called the Sandwich Theorem or the Pinching Theorem. It says that if g (x) is squeezed between f (x) and h (x) near a, and if f and h have the same limit L at a, then g is forced to have the same limit L at a.
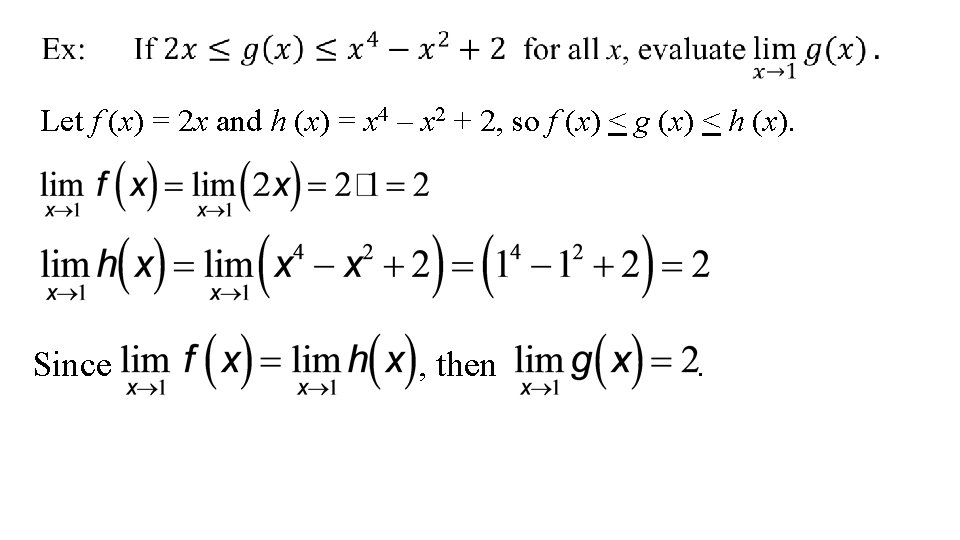
Let f (x) = 2 x and h (x) = x 4 – x 2 + 2, so f (x) < g (x) < h (x). Since , then .

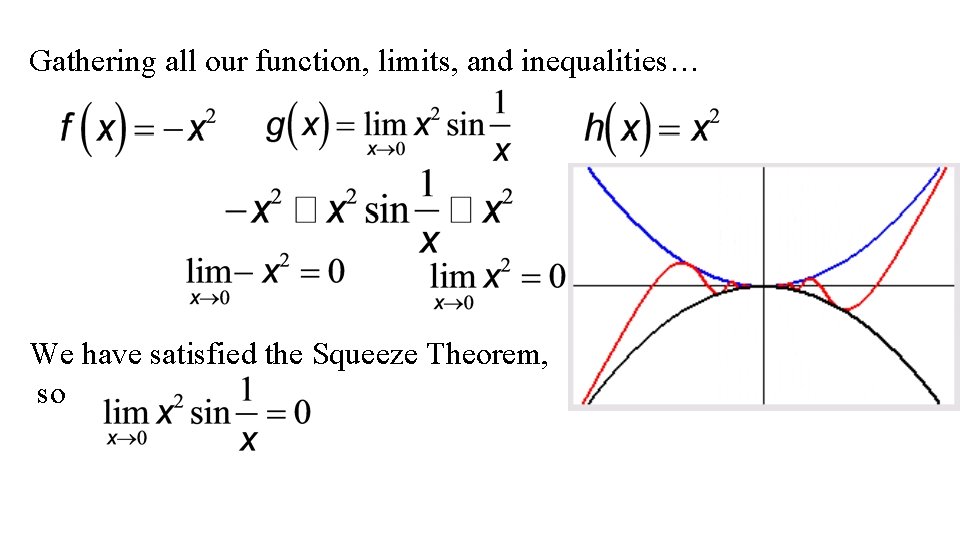
We can’t use the Product Law, because does not exist. We will have to apply the Squeeze Theorem, and will need a function f smaller than and a function h bigger than g such that both f (x) and h(x) approach 0. The sine of any number must range from -1 to 1, so…

Inequalities remain true if we multiply positive values to all the parts. x 2 > 0, so multiply all parts by x 2. The limits of the outer functions will be zero… …and can be our f and h functions.

Gathering all our function, limits, and inequalities… We have satisfied the Squeeze Theorem, so

1 0
 Calculating limits using the limit laws
Calculating limits using the limit laws Horizontal
Horizontal Real limits
Real limits Upper specification limit and lower specification limit
Upper specification limit and lower specification limit Upper specification limit and lower specification limit
Upper specification limit and lower specification limit Perbedaan limit kiri dan limit kanan
Perbedaan limit kiri dan limit kanan How to tell if the limit exists
How to tell if the limit exists Algor mortis
Algor mortis Calculating molar mass using colligative properties
Calculating molar mass using colligative properties Calculating time of death using algor mortis answers
Calculating time of death using algor mortis answers Facts about montesquieu
Facts about montesquieu Limit and continuity
Limit and continuity Section 3 using newtons laws
Section 3 using newtons laws Section 1 forces
Section 1 forces Section 3 using newtons laws
Section 3 using newtons laws Hình ảnh bộ gõ cơ thể búng tay
Hình ảnh bộ gõ cơ thể búng tay Lp html
Lp html Bổ thể
Bổ thể Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Chó sói
Chó sói Thang điểm glasgow
Thang điểm glasgow