Aim How can we use colligative properties to

Aim: How can we use colligative properties to determine the molar mass of a solute? H. W. Study p. 505 sample exercise 11. 8 p. 507 sample exercise 11. 10 pp. 508 -513 Ans. ques. p. 522 # 58, 64, 66, 67, 84, 100

I Determination of molar mass using freezing point depression Problem: 98. 0 g of a nonvolatile, non-electrolyte is dissolved in 950. g of benzene. The freezing point of this solution is found to be 0. 500 C. If the normal freezing point of benzene is 5. 500 C, what is the molar mass of the unknown solute? Kf for benzene is 5. 120 C • kg mol Ans: ΔTf = Kfm (i=1) m = ΔTf = 5. 000 C =. 977 kg Kf 5. 120 C • kg mol moles of solute = (0. 977 mol/kg)(. 950 kg) =. 928 mol solute

98. 0 g = molar mass. 928 mol 1 molar mass = 98. 0 g = 106 g/mol. 928 mol Problem: A solution of 8. 00 g acetic acid in 100. g benzene freezes at 2. 100 C. A solution of 8. 00 g acetic acid in 100. g water freezes at -2. 500 C. Find the molar mass of acetic acid from each of these data. What can you conclude about the state of acetic acid molecules dissolved in each of these solvents? How are these results related to the properties of the water and benzene molecules?

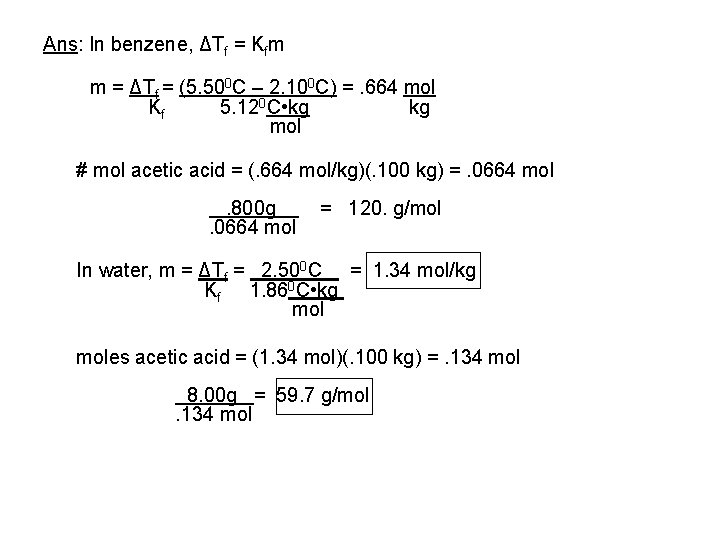
Ans: In benzene, ΔTf = Kfm m = ΔTf = (5. 500 C – 2. 100 C) =. 664 mol Kf 5. 120 C • kg kg mol # mol acetic acid = (. 664 mol/kg)(. 100 kg) =. 0664 mol. 800 g. 0664 mol = 120. g/mol In water, m = ΔTf = 2. 500 C = 1. 34 mol/kg Kf 1. 860 C • kg moles acetic acid = (1. 34 mol)(. 100 kg) =. 134 mol 8. 00 g = 59. 7 g/mol. 134 mol

The Kf in benzene = 5. 12 = 2. 75 Kf in water 1. 86 1 However, the molalities seem to indicate that there are fewer particles of acetic acid in the benzene than in the water. The acetic acid molecules, therefore, appear to be almost completely undissociated in benzene, and dissociated in water. In H 2 O: CH 3 COOH + H 2 O CH 3 COO-(aq) + H 3 O+(aq) In C 6 H 6: CH 3 COOH + C 6 H 6 → CH 3 COOH(aq)

Water is polar, benzene is not. The polar nature of water must promote the dissociation of a proton from the acid, while the nonpolar benzene molecules do not. The acid should be more soluble in water than in benzene. True M. W. CH 3 COOH = 60. g/mol

II A. Osmotic Pressure Semipermiable membrane – a membrane that permits the passage of some molecules, but not others. Osmosis – the net movement of solvent molecules from a solution of lower solute concentration, across a semipermeable membrane, to a solution of higher solute concentration. NOTE: osmosis is a dynamic process e. g. Osmosis stops as a result of added pressure due to the extra concentrated solution height (weight) of the fluid column (2). dilute solution semipermeable membrane 1. before osmosis net direction of osmosis 2. after osmosis

Even after osmosis stops, there still exists a difference between the concentrations of the two solutions. Osmotic Pressure (π) – the pressure that must be applied to the more concentrated solution in order to stop osmosis. π conc. solution = pressure applied to stop net movement of solvent dilute solution (or pure solvent) π = MRT where M = molarity of solution R = gas constant (. 08206 L • atm/mol • K) T = Kelvin temp. of the solution

Note: Since M = n , V π = n. RT = m. RT V MV where M = molar mass Problem: What is the osmotic pressure at 250 C of an aqueous solution that is 0. 001 M sucrose? Ans: π = MRT π = (. 0010 mol)(. 08206 L • atm )(298 K) L mol • K π =. 024 atm

B. Determination of molar mass using osmotic pressure Problem: A 50. 00 m. L sample of an aqueous solution is prepared containing 1. 08 g of a blood plasma protein, human serum albumen. The solution has an osmotic pressure of 5. 85 mm Hg at 250 C. What is the molar mass of the albumen? Ans: π = 5. 85 mm Hg x 1 atm = 7. 70 x 10 -3 atm 760 mm Hg π = MRT = n. RT = m. RT V MV M = molar mass = m. RT πV

molar mass = (1. 08 g)(. 08206 L • atm)(298 K) mol • K (7. 70 x 10 -3 atm)(. 0500 L) molar mass = 6. 86 x 104 g/mol Two solutions that have the same osmotic pressure are said to be isotonic. A solution that has a lower osmotic pressure (lower conc. ) than another is said to be hypotonic. A solution that has a higher osmotic pressure than another is said to be hypertonic.

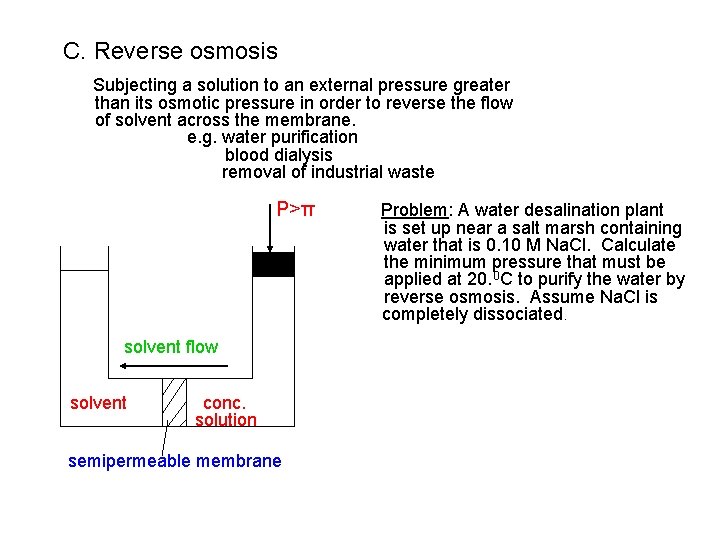
C. Reverse osmosis Subjecting a solution to an external pressure greater than its osmotic pressure in order to reverse the flow of solvent across the membrane. e. g. water purification blood dialysis removal of industrial waste P>π solvent flow solvent conc. solution semipermeable membrane Problem: A water desalination plant is set up near a salt marsh containing water that is 0. 10 M Na. Cl. Calculate the minimum pressure that must be applied at 20. 0 C to purify the water by reverse osmosis. Assume Na. Cl is completely dissociated.

Ans: Na. Cl(aq) → Na+(aq) + Cl-(aq) i=2 and π = i. MRT π = (2)(0. 10 mol)(. 08206 L • atm)(293 K) L mol • K π = 4. 8 atm Actually, π > 4. 8 atm should be applied