vwo AC Samenvatting Hoofdstuk 7 Oneindige intervallen a

vwo A/C Samenvatting Hoofdstuk 7

Oneindige intervallen a x ≤ 4½ ● l 4½ ‹ , 4½ ] b x > -8 ‹ -8 , › ○ l -8 7. 1

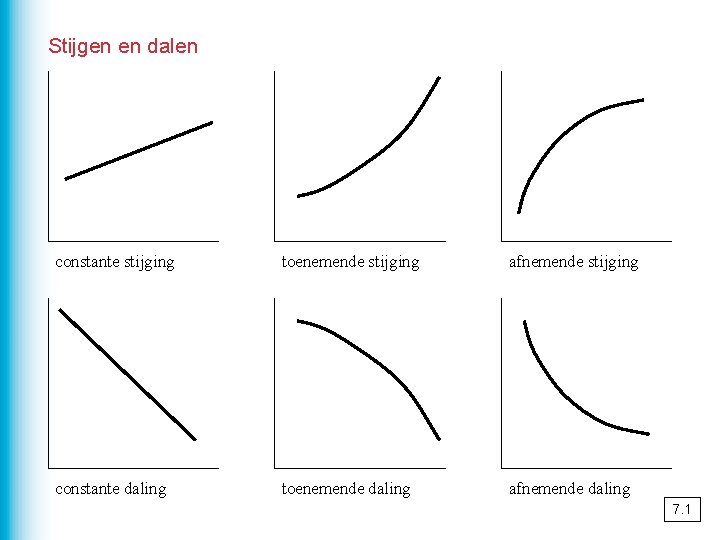
Stijgen en dalen constante stijging toenemende stijging afnemende stijging constante daling toenemende daling afnemende daling 7. 1

Toenamendiagram De toenamen en afnamen van een grafiek kun je verwerken in een toenamendiagram : 1 kies een stapgrootte 2 bereken voor elke stap de toename of afname 3 teken de staafjes omhoog bij toename en omlaag bij afname 4 teken het staafje bij de rechtergrens 5 bv. toename van 3 4 teken je het staafje bij 4 7. 1

. y . . voorbeeld . 0 . . x 7. 1

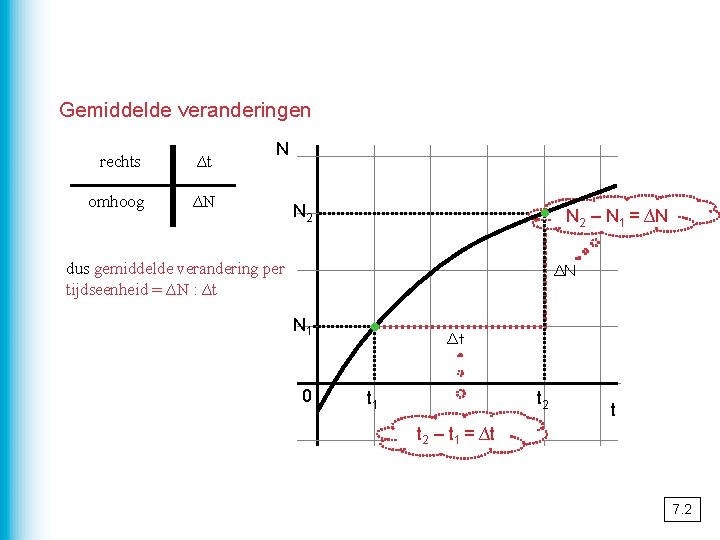
Gemiddelde veranderingen rechts ∆t omhoog ∆N N · N 2 dus gemiddelde verandering per tijdseenheid = ∆N : ∆t N 1 · 0 t 1 N 2 – N 1 = ∆N ∆N ∆t t 2 – t 1 = ∆t 7. 2

. Het differentiequotiënt van y op het interval [x. A, x. B] is y f(b) y. B B . ∆y ∆y A f(a) y. A ∆x 0 xa. A differentiequotiënt = ∆y : ∆x = gemiddelde verandering van y op [x. A, x. B] = r. c. = hellingsgetal van de lijn AB ∆x ∆y ∆x x xb. B = y. B – y. A x. B – x. A = f(b) – f(a) b - a 7. 2

Gemiddelde snelheid In een tijd-afstandgrafiek is de afgelegde s uitgezet tegen de tijd t Bij een tijd-afstandgrafiek geeft het differentiequotiënt op [a, b] de gemiddelde snelheid is ∆s ∆t 7. 2

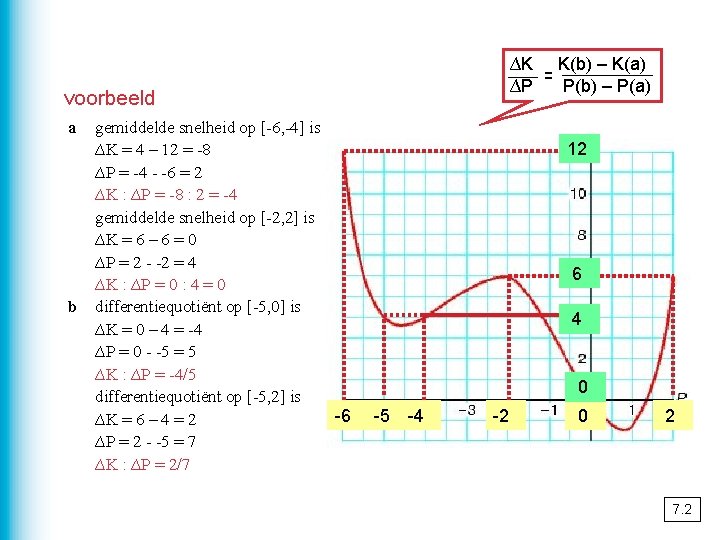
∆K K(b) – K(a) = ∆P P(b) – P(a) voorbeeld a b gemiddelde snelheid op [-6, -4] is ∆K = 4 – 12 = -8 ∆P = -4 - -6 = 2 ∆K : ∆P = -8 : 2 = -4 gemiddelde snelheid op [-2, 2] is ∆K = 6 – 6 = 0 ∆P = 2 - -2 = 4 ∆K : ∆P = 0 : 4 = 0 differentiequotiënt op [-5, 0] is ∆K = 0 – 4 = -4 ∆P = 0 - -5 = 5 ∆K : ∆P = -4/5 differentiequotiënt op [-5, 2] is -6 ∆K = 6 – 4 = 2 ∆P = 2 - -5 = 7 ∆K : ∆P = 2/7 12 6 4 0 -5 -4 -2 0 2 7. 2

Snelheid bij een tijd-afstand grafiek waarvan de formule bekend is, benader je de snelheid op het moment t = a door het differentiequotiënt te berekenen op een klein interval [a , a + ∆t] met bijvoorbeeld ∆t = 0, 001 7. 3

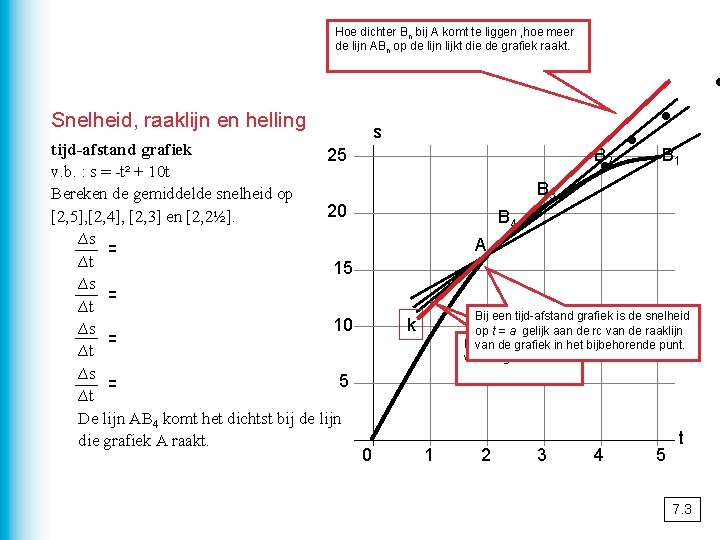
Hoe dichter Bn bij A komt te liggen , hoe meer de lijn ABn op de lijn lijkt die de grafiek raakt. Snelheid, raaklijn en helling tijd-afstand grafiek 25 v. b. : s = -t² + 10 t Bereken de gemiddelde snelheid op 20 [2, 5], [2, 4], [2, 3] en [2, 2½]. ∆s 25 – 16 = = 3 m/s ∆t 5– 2 15 ∆s 24 – 16 = 4 m/s = ∆t 4– 2 10 ∆s 21 – 16 = 5 m/s = ∆t 3– 2 ∆s 18, 75 – 16 5 = 5, 5 m/s = ∆t 2, 5 – 2 De lijn AB 4 komt het dichtst bij de lijn die grafiek A raakt. s . . B 2 B 3 B 1 B 4 A Bij een tijd-afstand grafiek is de snelheid op t = a gelijk aan de rc van de raaklijn Devan lijn de k isgrafiek de raaklijn in het bijbehorende punt. van de grafiek in A. k 0 1 2 3 4 5 t 7. 3

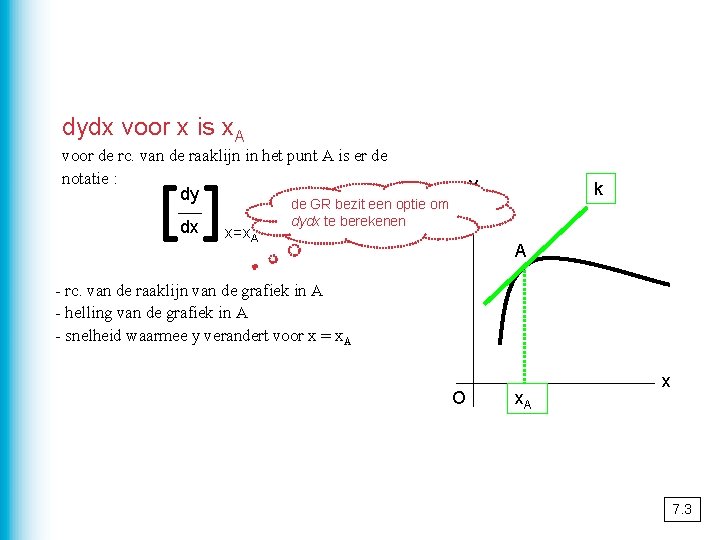
dydx voor x is x. A voor de rc. van de raaklijn in het punt A is er de notatie : [] dy dx x=x. A y k de GR bezit een optie om dydx te berekenen A - rc. van de raaklijn van de grafiek in A - helling van de grafiek in A - snelheid waarmee y verandert voor x = x. A O x. A x 7. 3

7. 3

Het opstellen van de formule van een raaklijn voer in y 1 = x² + x – 2 stel k : y = ax + b met a = [] dy dx = -1 dus k : y = -x + b f(-1) = -2 dus A(-1, -2) -2 = - -1 + b -2 = 1 + b -3 = b k : y = -x - 3 7. 3

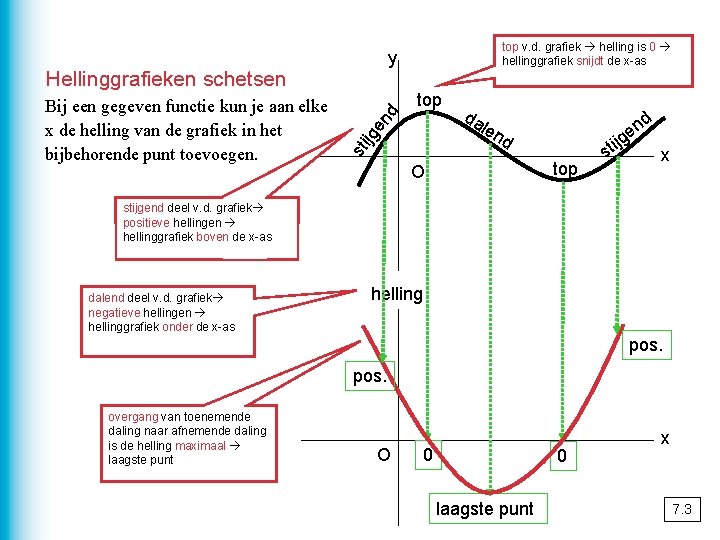
y Hellinggrafieken schetsen d top da d len sti jg en Bij een gegeven functie kun je aan elke x de helling van de grafiek in het bijbehorende punt toevoegen. top v. d. grafiek helling is 0 hellinggrafiek snijdt de x-as d top O sti n jge x stijgend deel v. d. grafiek positieve hellingen hellinggrafiek boven de x-as dalend deel v. d. grafiek negatieve hellingen hellinggrafiek onder de x-as helling pos. overgang van toenemende daling naar afnemende daling is de helling maximaal laagste punt O 0 0 laagste punt x 7. 3

Hellinggrafiek plotten m. b. v. GR TI MATH – MATH - menu optie n. Deriv Casio OPTN – CALC – menu optie d/dx vb. voer in y 1 = 0, 1 x 4 – x 2 + x + 8 en y 2 = n. Deriv(y 1, x, x) (op de TI) of y 2 = d/dx(y 1, x) (op de Casio) 7. 3

De afgeleide functie bij een functie hoort een hellingfunctie i. p. v. hellingfunctie wordt meestal de naam afgeleide functie of afgeleide gebruikt notatie : f’ (f-accent) regels voor de afgeleide : f(x) = a geeft f’(x) = 0 f(x) = ax geeft f’(x) = a f(x) = ax² geeft f’(x) = 2 ax 7. 4

de afgeleide van f(x) = ax 3 f’(x) = 3 ax² g(x) = ax 4 g’(x) = 4 ax 3 oude exponent ervoor zetten nieuwe exponent 1 minder (4 - 1 = 3) h(x) = ax 5 h’(x) = 5 ax 4 algemeen geldt : k(x) = axn k’(x) = n · axn-1 somregel van het differentiëren f(x) = g(x) + h(x) f’(x) = g’(x) + h’(x) 7. 4

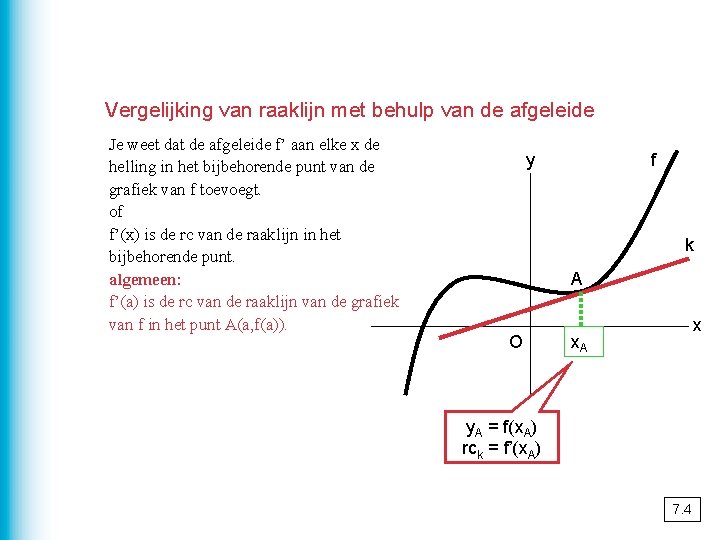
Vergelijking van raaklijn met behulp van de afgeleide Je weet dat de afgeleide f’ aan elke x de helling in het bijbehorende punt van de grafiek van f toevoegt. of f’(x) is de rc van de raaklijn in het bijbehorende punt. algemeen: f’(a) is de rc van de raaklijn van de grafiek van f in het punt A(a, f(a)). y f k A O x x. A y. A = f(x. A) rck = f’(x. A) 7. 4

Notaties voor de afgeleide notaties voor de afgeleide van y = f(x) zijn : dy dx f’(x) d dx (f(x)) df(x) dx 7. 5

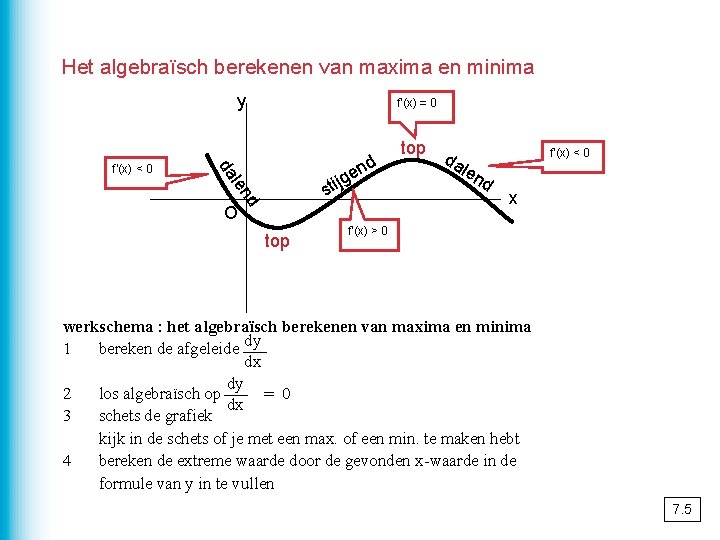
Het algebraïsch berekenen van maxima en minima y nd e jg da f’(x) < 0 f’(x) = 0 len sti d O top d ale f’(x) < 0 nd x f’(x) > 0 werkschema : het algebraïsch berekenen van maxima en minima 1 bereken de afgeleide dy dx dy 2 los algebraïsch op = 0 dx 3 schets de grafiek kijk in de schets of je met een max. of een min. te maken hebt 4 bereken de extreme waarde door de gevonden x-waarde in de formule van y in te vullen 7. 5