Vn vc t php tuyn trong h Trong

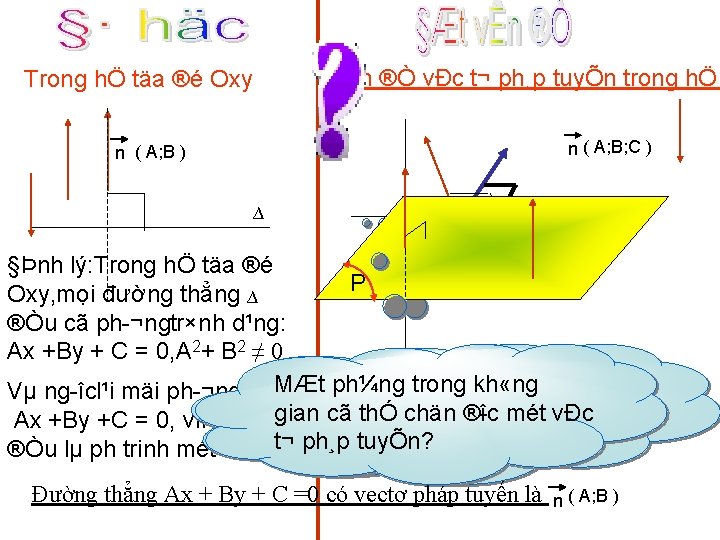
VÊn ®Ò vÐc t¬ ph¸p tuyÕn trong hÖ Trong hÖ täa ®é Oxy n ( A; B; C ) n ( A; B ) ∆ ∆ §Þnh lý: Trong hÖ täa ®é P Oxy, mọi đường thẳng ∆ ®Òu cã ph ¬ngtr×nh d¹ng: Ax +By + C = 0, A 2+ B 2 ≠ 0 T¹i MÆt sao ph¼ng ® êng trong th¼ngkh «ng trong kh «ng Vµ ng îcl¹i mäi ph ¬ngtr×nh 2 gian kh «ng thÓ chän ® îc mét vÐc Ax +By +C = 0, víi A 2 +Bgian ≠ 0 cã t¬ t¬ th¼ng ph¸p tuyÕn? ®Òu lµ ph trinh mét dường Đường thẳng Ax + By + C =0 có vectơ pháp tuyến là n ( A; B )

vÐc t¬ ph¸p tuyÕn cña mÆt ph¼ng ph ¬ngtr×nh tæng qu¸t cña mÆt ph¼ng 1. VÐc t¬ ph¸p tuyÕn cña mÆt ph¼ng n n ( A; B; C ) lµ vÐc t¬ ph¸p tuyÕn cña mp (P) ≠ n n 0 (P) A 2+ B 2 + C 2 ≠ 0 n (P) P kn C¸c vÐc t¬ k n còng lµ vÐc t¬ ph¸p tuyÕn Bài toán: Trong không gian Oxyz cho mp (P) và 2 vectơ không cùng phươn a = (a 1, a 2, a 3), b = (b 1, b 2, b 3) có giá song hoặc nằm trong mặt phẳng (P) Vectơ Ng h = (a 2 b 3 – a 3 b 2; a 3 b 1 – a 1 b 3; a 1 b 2 – a 2 b 1) ghi e tóm tắt : được gọi là vectơ pháp tuyến của mp (P). Kí hiệu: n n = a ^ b hoặc = [a , b ] là tích có hướng của 2 vectơ

HĐ 1: Trong không gian Oxyz cho A(2; 1; 3), B(4; 0; 1), C( 10; 5; 3). Hãy tính vectơ pháp tuyến của mp(ABC). Bµi gi¶i Vtpt n = [AB; AC] AB = ( 2; 1 ; 2) AC = ( 12; 6 ; 0) Vtpt n = [AB; AC] = (12 ; 24) Hay n = (1; 2; 2)

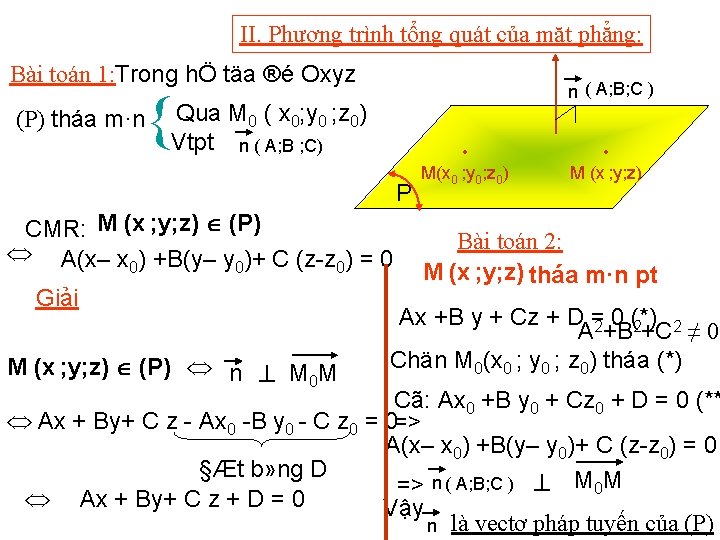
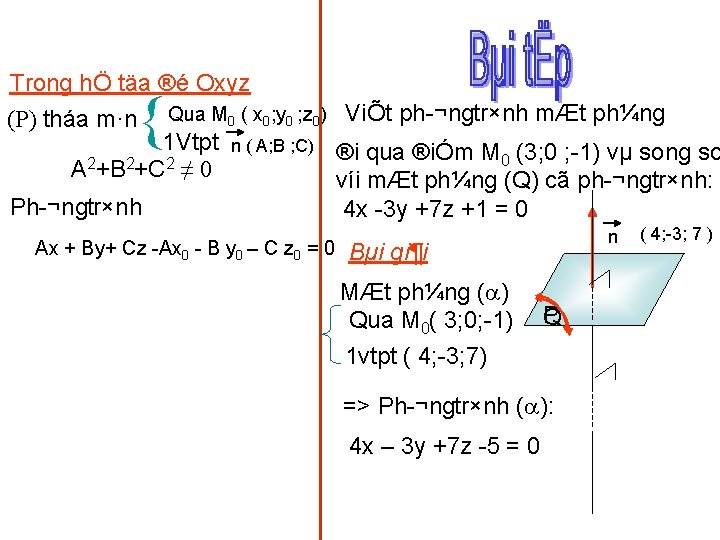
II. Phương trình tổng quát của mặt phẳng: Bài toán 1: Trong hÖ täa ®é Oxyz (P) tháa m·n n ( A; B; C ) Qua M 0 ( x 0; y 0 ; z 0) Vtpt n ( A; B ; C) P CMR: M (x ; y; z) (P) A(x– x 0) +B(y– y 0)+ C (z z 0) = 0 Giải M (x ; y; z) (P) n M 0 M • M(x 0 ; y 0; z 0) • M (x ; y; z) Bài toán 2: M (x ; y; z) tháa m·n pt Ax +B y + Cz + D =2 0 (*) A +B 2+C 2 ≠ 0 Chän M 0(x 0 ; y 0 ; z 0) tháa (*) Cã: Ax 0 +B y 0 + Cz 0 + D = 0 (** Ax + By+ C z Ax 0 B y 0 C z 0 = 0=> A(x– x 0) +B(y– y 0)+ C (z z 0) = 0 §Æt b» ng D => n ( A; B; C ) M 0 M Ax + By+ C z + D = 0 Vậy n là vectơ pháp tuyến của (P)

1. Định nghĩa: Phương trình có dạng Ax + By + Cz + D = 0, A 2 + B 2+C 2 ≠ 0, được gọi là phương trình tổng quát của mặt phẳng. *) Nhận xét: a) Nếu mp (P) có phương trình tổng quát là Ax + By + n = ( A; B ; C) Cz + D = 0 thì nó có 1 vtpt là b) Phương trình mp đi qua điểm M 0(x 0, y 0, z 0) nhận n = ( A; B ; C) vectơ khác vectơ không làm vectơ pháp tuyến là A(x – x 0) + B(y – y 0) + C(z – z 0) = 0.

HĐ 2: Cho mp (P): 4 x – 2 y – 6 z + 7 = 0 Tìm 1 vtpt của (P)? Giải: n = ( 4; 2 ; 6)

HĐ 3: Lập phương trình tổng quát của mp(MNP) với M(1; 1; 1), N(4; 3; 2), P(5; 2; 1) Giải: Vtpt n = [MN; MP] MN = ( 3; 2 ; 1) MP = ( 4; 1 ; 0) Vtpt n = [MN; MP] = ( 1 ; 4 ; 5) Pt mp (MNP) qua M(1; 1; 1 ) nhận n = ( 1 ; 4 ; 5) làm vtc Pt. (ABC) lµ : 1(x – 1) + 4(y – 1) – 5(z – 1) = 0 hay x + 4 y 5 z + 2 = 0

2. Các trường hợp riêng: Trong không gian Oxyz cho mp(P): Ax + By + Cz +D= 0(1) a) Nếu D = 0 (P) đi qua gốc toạ độ O. b) Nếu hệ số A bắng 0 (P) // Ox hoặc (P) chứa trục Ox HĐ 4: Nêu trường hợp nếu B = 0 hoặc C = 0? ) ĐA: B = 0 (P) // Oy hoặc chứa trục Oy C = 0 (P) // Oz hoặc chứa trục Oz. c) Nếu A = B = 0, C ≠ 0 (P) // hoặc trùng mp(Oxy HĐ 5: Nếu A = C = 0, B ≠ 0 (P) // hoặc trùng mp(Oxz) Nếu B = C = 0, A ≠ 0 (P) // hoặc trùng mp(Oyz)

*) Nhận xét: Phương trình mặt phẳng đi qua 3 điểm A(a; 0; 0), B(0; b; 0), C(0; 0; c) là: z =1 x + y + a b c Ví dụ : ViÕt ph ¬ngtr×nh mÆt ph¼ng §i qua 3 ®iÓm A( 1; 0; 0) , B(0; 2; 0), C (0; 0; 5) Bµi gi¶i z =1 x + y + 1 2 5 Ph. tr×nh mp (ABC) : 10 x 5 y + 2 z 10 = 0

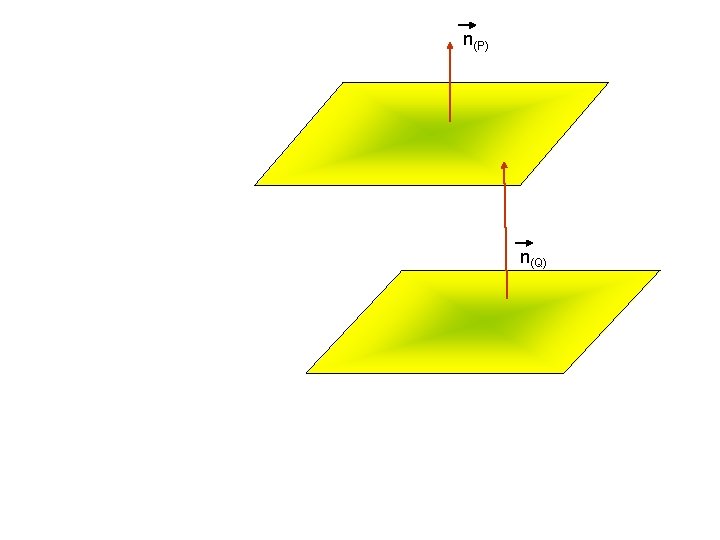
III. Điều kiện để hai mặt phẳng song, vuông góc HĐ 6: cho hai mp (P): x – 2 y + 3 z + 1 = 0 (Q): 2 x – 4 y + 6 z + 1= 0 Có nhận xét gì về vectơ pháp tuyến của chúng? Trả lời: n(P) = (1; 2; 3) n(Q)= (2; 4; 6) = 2(1; 2; 3) = 2 n(P) Hai mp (P) và (Q) được gọi là hai mp song.

n(P) n(Q)

1. Điều kiện để hai mp song Cho 2 mp: (P): A 1 x + B 1 y + C 1 z + D 1= 0 có vtpt n(P) = (A 1; B 1; C 1) (Q): A 2 x + B 2 y + C 2 z + D 2 = 0 có vtpt n(Q) = (A 2; B 2; C 2) (P) // (Q) n(P) = k n(Q) D 1 ≠ k. D 2 (A 1; B 1; C 1) = k(A 2; B 2; C 2) D 1 ≠ k. D 2

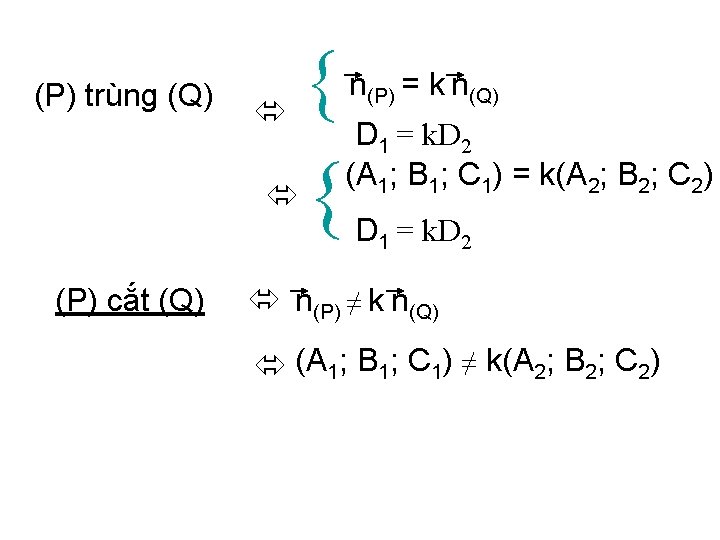
(P) trùng (Q) (P) cắt (Q) n(P) = k n(Q) D 1 = k. D 2 (A 1; B 1; C 1) = k(A 2; B 2; C 2) D 1 = k. D 2 n(P) ≠ k n(Q) (A 1; B 1; C 1) ≠ k(A 2; B 2; C 2)

Trong hÖ täa ®é Oxyz (P) tháa m·n Qua M 0 ( x 0; y 0 ; z 0) ViÕt ph ¬ngtr×nh mÆt ph¼ng 1 Vtpt n ( A; B ; C) ®i qua ®iÓm M (3; 0 ; 1) vµ song so 0 A 2+B 2+C 2 ≠ 0 víi mÆt ph¼ng (Q) cã ph ¬ngtr×nh: Ph ¬ngtr×nh 4 x 3 y +7 z +1 = 0 Ax + By+ Cz Ax 0 B y 0 – C z 0 = 0 n Bµi gi¶i MÆt ph¼ng ( ) Qua M 0( 3; 0; 1) 1 vtpt ( 4; 3; 7) P Q => Ph ¬ngtr×nh ( ): 4 x – 3 y +7 z 5 = 0 ( 4; 3; 7 )

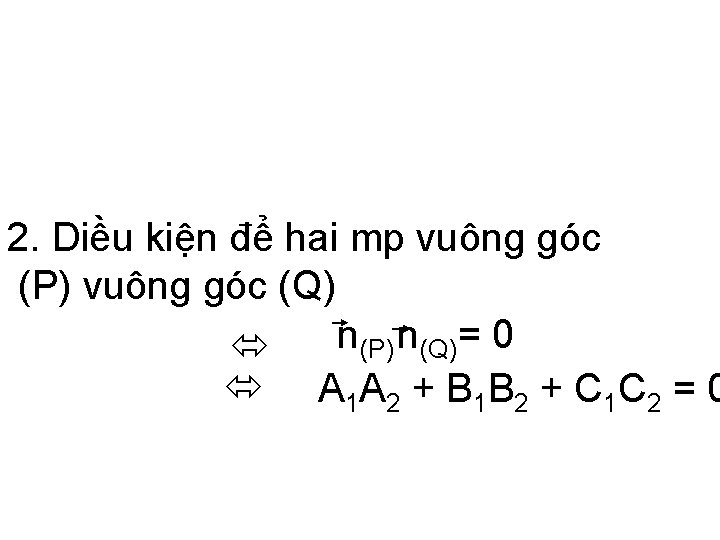
2. Diều kiện để hai mp vuông góc (P) vuông góc (Q) n(P). n(Q)= 0 A 1 A 2 + B 1 B 2 + C 1 C 2 = 0

Ví dụ: §i qua A(2; 3; 1) vµ B ( 0 ; 1 ; 2) ViÕt pt mÆt ph¼ng (P) tháa m·n : (Q)_cã pt: 3 x + 5 y 4 z + 7 = 0 Bµi gi¶i V× (P) (Q) và (P) qua A, B => hai vectơ không cùng phương có gi song hoặc nằm trên (P) là AB ( 2; 4; 3) n(Q)(3; 5; 4) => VÐc t¬ n(P) = [ n(Q) , AB] = (1; 17 ; 22) lµ vÐc t¬ ph¸p tuyÕn c (P) Qua A(2; 3; 1) => Ph ¬ngtr×nh (P) lµ 1(x – 2) + 17(y+3) + 22(z 1) = 0 Hay x + 17 y + 22 z + 27 = 0

§i qua A(2; 3; 1) vµ B ( 0 ; 1 ; 2) Cho mÆt ph¼ng (P) tháa m·n : (Q)_cã pt: 3 x + 5 y 4 z + 7 = 0 KÕt luËn nµo sau ®©y ®óng? a) VÐc t¬ u = ( 3 ; 5 ; 4) lµ vÐc t¬ ph¸p tuyÕn cña (P). b) VÐc t¬ v = ( 2 ; 4 ; 3) lµ vÐc t¬ ph¸p tuyÕn cña (P). c) VÐc t¬ n = [ u , v] = (1; 17 ; 22) lµ vÐc t¬ ph¸p tuyÕn cña (P)

Trong hÖ täa ®é Oxyz Bµi 1: Trong hÖ to¹ ®é Oxyz cho A( 1; 3; 0), B( 5; 7 ; 4) 1 Vtpt n ( A; B ; C) A 2+B 2+C 2 ≠ 0 ViÕt ph ¬ngtr×nh mÆt ph¼ng trung Ph ¬ngtr×nh trùc cña ®o¹n AB Bµi gi¶i A(x – x 0) + B(y – y 0)+ C(z – z 0) = 0 Gäi (P) lµ mÆt ph¼ng trung trùc AB Ng îcl¹i (2; 2; 2) Tõ pt: Ax + By+ C z + D = 0 (P) tháa m·n Qua I ? 1 Vtpt AB n =? (6; 10; 4) Víi: A 2+B 2+C 2 ≠ 0 Ph ¬ngtr×nh (P): Chän ® îc: M (x ; y ; z ) tháa (*) (P) tháa m·n Qua M 0 ( x 0; y 0 ; z 0) 0 0 Vµ mét vÐc t¬ ph¸p tuyÕn n ( A; B; C ) 3 x 5 y +2 z – 20 = 0

Bµi tËp : Trong hÖ täa ®é Oxyz Cho hai mÆt ph¼ng (P) vµ (Q)_ lÇn (P) tháa m·n Qua M 0 ( x 0; y 0 ; z 0) l îtcã ph ¬ngtr×nh: 1 Vtpt n ( A; B ; C) 3 x + 2 y 5 z +4 = 0, x 7 y +6 z 1 = 0 A 2+B 2+C 2 ≠ 0 Mét ®iÓm M 0 ( 1; 4; 0). ViÕt ph ¬ngtr×nh mÆt ph¼ng( ) qu Ph ¬ngtr×nh vµ ®ång thêi vu «ng gãc víi c¶ hai mÆ Ax + By+ Cz Ax 0 B y 0 – C z 0 = 0 ph¼ng (P) vµ (Q). * MÆt ph¼ng (P) (Q) Bµi gi¶i: n(P). n(Q)= 0 *) (P) // (Q) chung vtpt V× ( ) (P) => ( ) cã 1 vtcp u (3; 2; 5 V× ( ) (Q) => ( ) cã 1 vtcp v (1; 7; 6 [u, v] = ( 23; 7 ; 23) ≠ 0 Chän vtpt cña ( ) lµ n (23; 7; 23) ( ) qua M 0(1; 4 ; 0) => Ph. tr×nh ( ) lµ 23 x +7 y +23 z +5 =

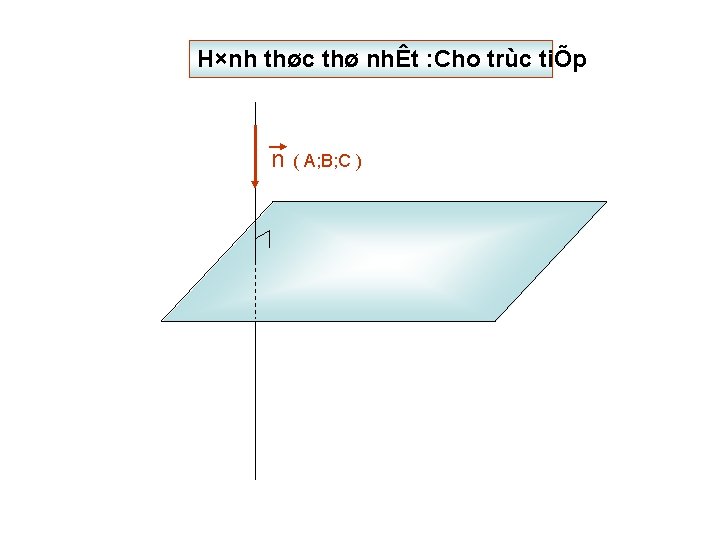
H×nh thøc thø nhÊt : Cho trùc tiÕp n ( A; B; C )

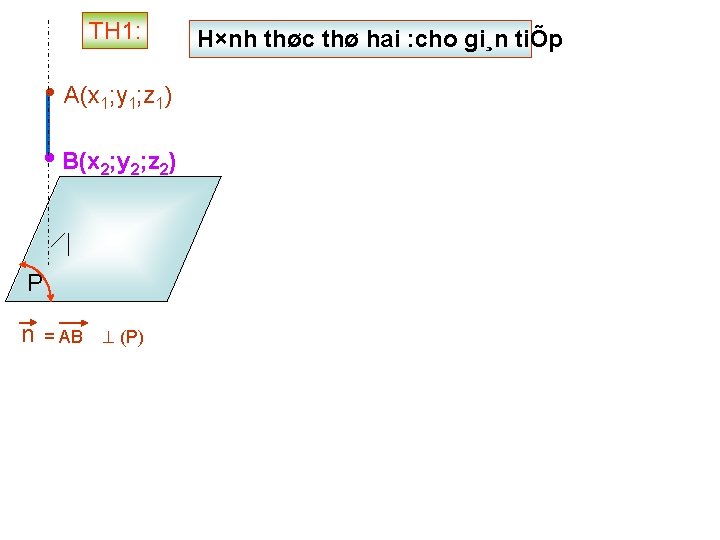
TH 1: • A(x 1; y 1; z 1) • B(x 2; y 2; z 2) P n = AB (P) H×nh thøc thø hai : cho gi¸n tiÕp

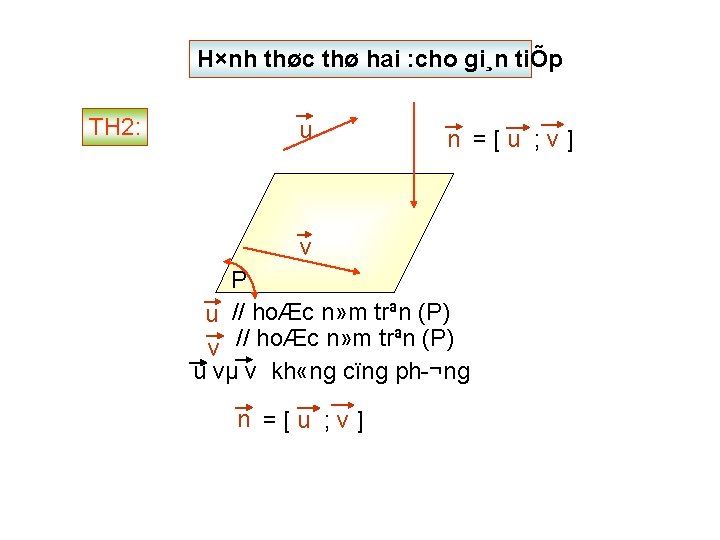
H×nh thøc thø hai : cho gi¸n tiÕp TH 2: u n =[u ; v] v P u // hoÆc n» m trªn (P) v // hoÆc n» m trªn (P) u vµ v kh «ng cïng ph ¬ng n =[u ; v]

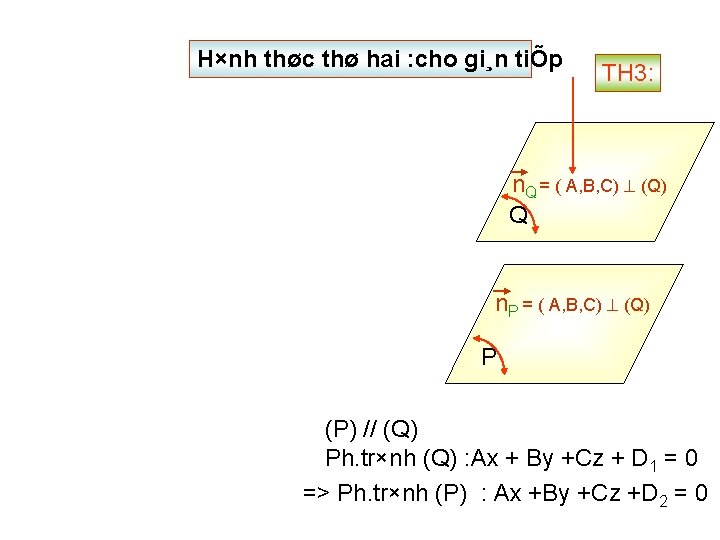
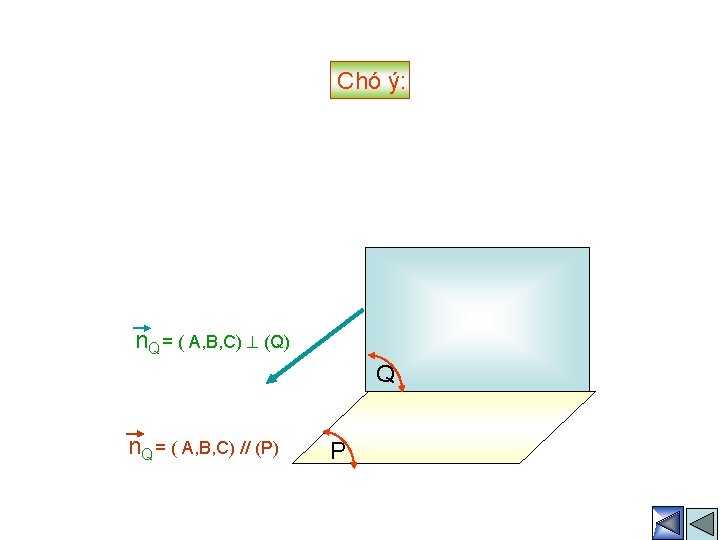
H×nh thøc thø hai : cho gi¸n tiÕp TH 3: n. Q = ( A, B, C) (Q) Q n. P = ( A, B, C) (Q) P (P) // (Q) Ph. tr×nh (Q) : Ax + By +Cz + D 1 = 0 => Ph. tr×nh (P) : Ax +By +Cz +D 2 = 0

IV. Khoảng cách từ một điểm đến một mặt phẳng Định lí: Trong không gian Oxyz cho mp (P) : Ax + By + Cz + D = 0 và điểm M 0(x 0; y 0; z 0). Khoảng cách từ M 0 đến mp (P), kí hiệu d(M 0, (P))

Ví dụ: Tính khoảng cách từ gốc toạ độ O đến mp(P): 2 x + 2 y –z + 3 = 0 Giải:

Ví dụ 2: Tính khoảng cách giữa hai mp song (P): x + 2 y + 2 z + 11 = 0 (Q): x + 2 y + 2 z + 2 = 0 Giải: Lấy M(0; 0; 1) thuộc (Q)

HĐ 7: Tính khoảng cách giữa 2 mp (P): x – 2 = 0 (Q): x – 8 = 0 Giải: Lấy M(2, 0, 0) thuộc (P)

I. Lý thuyÕt : • N¾m v÷ng bµi to¸n c¬ b¶n vÒ viÕt ph ¬ngtr×nh mÆt ph¼ng. (Ph¶i biÕt mét ®iÓm cña mÆt ph¼ vµ mét Vtpt cña mÆt ph¼n • N¾m v÷ng c¸ch x¸c ®Þnh mét vÐc chØ ph ¬ngcña mÆt ph¼ng • N¾m v÷ng c¸ch x¸c ®Þnh mét vÐc ph¸p tuyÕn cña mÆt ph¼ng I • Bµi tËp: Tõ 1 ®Õn 10 trang 81 vµ 82 (Sgk)

10