Unsupervised Learning Clustering Dimensionality Reduction 273 A Intro

Unsupervised Learning Clustering & Dimensionality Reduction 273 A Intro Machine Learning

What is Unsupervised Learning? • In supervised learning we were given attributes & targets (e. g. class labels). In unsupervised learning we are only given attributes. • Our task is to discover structure in the data. • Example I: the data may be structured in clusters: • Example II: the data may live on a lower dimensional manifold: Is this a good clustering?

Why Discover Structure ? • Data compression: If you have a good model you can encode the data more cheaply. • Example: To encode the data I have to encode the x and y position of each data-case. However, I could also encode the offset and angle of the line plus the deviations from the line. Small numbers can be encoded more cheaply than large numbers with the same precision. • This idea is the basis for model selection: The complexity of your model (e. g. the number of parameters) should be such that you can encode the data-set with the fewest number of bits (up to a certain precision).

Why Discover Structure ? the a on. . . • Often, the result of an unsupervised learning algorithm is a new representation for the same data. This new representation should be more meaningful and could be used for further processing (e. g. classification). • Example I: Clustering. The new representation is now given by the label of a cluster to which the data-point belongs. This tells us how similar data-cases are. • Example II: Dimensionality Reduction. Instead of a 100 dimensional vector of real numbers, the data are now represented by a 2 dimensional vector which can be drawn in the plane. • The new representation is smaller and hence more convenient computationally. • Example I: A text corpus has about 1 M documents. Each document is represented as a 20, 000 dimensional count vector for each word in the vocabulary. Dimensionality reduction turns this into a (say) 50 dimensional vector for each doc. However: in the new representation documents which are on the same topic, but do not necessarily share keywords have moved closer together! 5 4 7 0 0 0 1 3 5 0 0 0 1 0 0 0 4 0 0 1. . .

Clustering: K-means • We iterate two operations: 1. Update the assignment of data-cases to clusters 2. Update the location of the cluster. • Denote the assignment of data-case “i” to cluster “c”. • Denote the position of cluster “c” in a d-dimensional space. the location of data-case i • Then iterate until convergence: 1. For each data-case, compute distances to each cluster and the closest one: 2. For each cluster location, compute the mean location of all data-cases assigned to it: Nr. of data-cases in cluster c Set of data-cases assigned to cluster c

K-means • Cost function: • Each step in k-means decreases this cost function. • Often initialization is very important since there are very many local minima in C. Relatively good initialization: place cluster locations on K randomly chosen data-cases. • How to choose K? Add complexity term: Or X-validation Or Bayesian methods and minimize also over K

Vector Quantization • K-means divides the space up in a Voronoi tesselation. • Every point on a tile is summarized by the code-book vector “+”. This clearly allows for data compression !

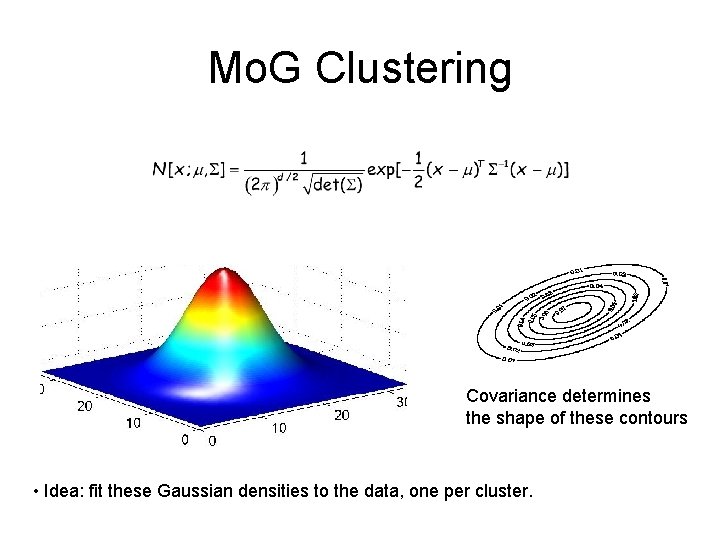
Mixtures of Gaussians • K-means assigns each data-case to exactly 1 cluster. But what if clusters are overlapping? Maybe we are uncertain as to which cluster it really belongs. • The mixtures of Gaussians algorithm assigns data-cases to cluster with a certain probability.

Mo. G Clustering Covariance determines the shape of these contours • Idea: fit these Gaussian densities to the data, one per cluster.

EM Algorithm: E-step • “r” is the probability that data-case “i” belongs to cluster “c”. • is the a priori probability of being assigned to cluster “c”. • Note that if the Gaussian has high probability on data-case “i” (i. e. the bell-shape is on top of the data-case) then it claims high responsibility for this data-case. • The denominator is just to normalize all responsibilities to 1:

EM Algorithm: M-Step total responsibility claimed by cluster “c” expected fraction of data-cases assigned to this cluster weighted sample mean where every data-case is weighted according to the probability that it belongs to that cluster. weighted sample covariance

EM-Mo. G • EM comes from “expectation maximization”. We won’t go through the derivation. • If we are forced to decide, we should assign a data-case to the cluster which claims highest responsibility. • For a new data-case, we should compute responsibilities as in the E-step and pick the cluster with the largest responsibility. • E and M steps should be iterated until convergence (which is guaranteed). • Every step increases the following objective function (which is the total log-probability of the data under the model we are learning):

Dimensionality Reduction • Instead of organized in clusters, the data may be approximately lying on a (perhaps curved) manifold. • Most information in the data would be retained if we project the data on this low dimensional manifold. • Advantages: visualization, extracting meaning attributes, computational efficiency

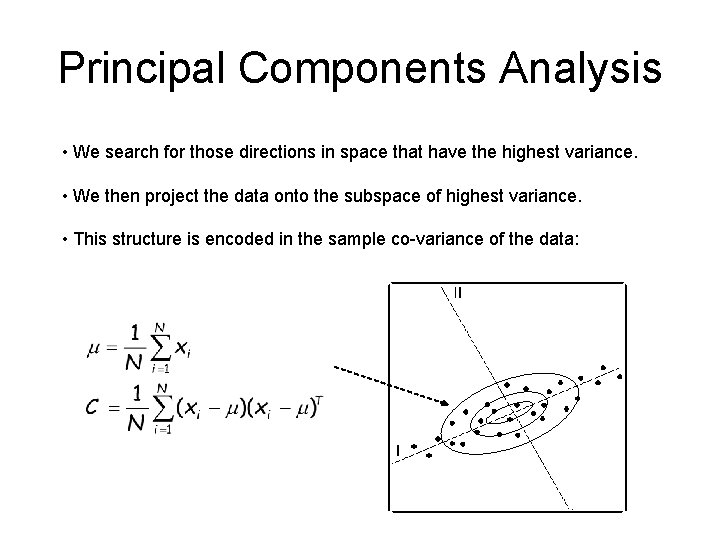
Principal Components Analysis • We search for those directions in space that have the highest variance. • We then project the data onto the subspace of highest variance. • This structure is encoded in the sample co-variance of the data:

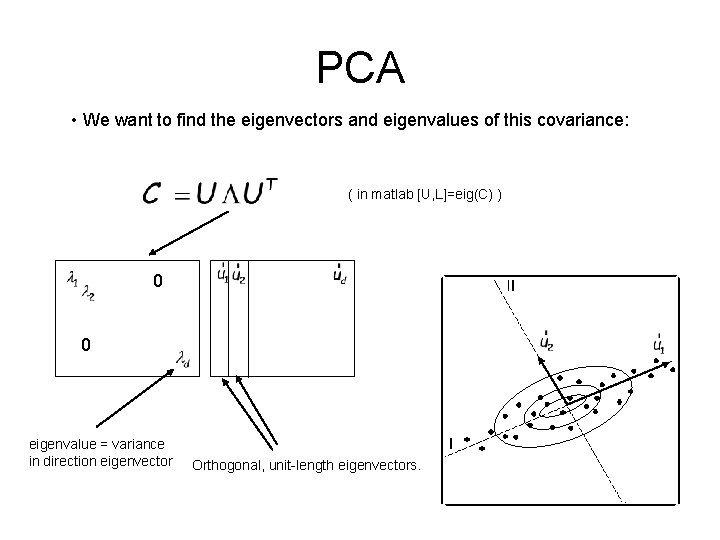
PCA • We want to find the eigenvectors and eigenvalues of this covariance: ( in matlab [U, L]=eig(C) ) 0 0 eigenvalue = variance in direction eigenvector Orthogonal, unit-length eigenvectors.

PCA properties (U eigevectors) (u orthonormal U rotation) 0 0 (rank-k approximation) (projection)

PCA properties is the optimal rank-k approximation of C in Frobenius norm. I. e. it minimizes the cost-function: Note that there are infinite solutions that minimize this norm. If A is a solution, then is also a solution. The solution provided by PCA is unique because U is orthogonal and ordered by largest eigenvalue. Solution is also nested: if I solve for a rank-k+1 approximation, I will find that the first k eigenvectors are those found by an rank-k approximation (etc. )