Traffic Matrix Estimation for Traffic Engineering Mehmet Umut

Traffic Matrix Estimation for Traffic Engineering Mehmet Umut Demircin

Traffic Engineering (TE) n Tasks ¨ Load balancing ¨ Routing protocols configuration ¨ Dimensioning ¨ Provisioning ¨ Failover strategies

Particular TE Problem n Optimizing routes in a backbone network in order to avoid congestions and failures. ¨ Minimize the max-utilization. ¨ MPLS (Multi-Protocol Label Switching) n Linear programming solution to a multi-commodity flow problem. ¨ Traditional shortest path routing (OSPF, n Compute set of link weights that minimize congestion. IS-IS)

Traffic Matrix (TM) n n n A traffic matrix provides, for every ingress point i into the network and every egress point j out of the network, the volume of traffic Ti, j from i to j over a given time interval. TE utilizes traffic matrices in diagnosis and management of network congestion. Traffic matrices are critical inputs to network design, capacity planning and business planning.

Traffic Matrix (cont’d) n Ingress and egress points can be routers or Po. Ps.

Determining the Traffic Matrix n Direct Measurement: TM is computed directly by collecting flowlevel measurements at ingress points. Additional infrastructure needed at routers. (Expensive!) n May reduce forwarding performance at routers. n Terabytes of data per day. n Solution = Estimation

TM Estimation n Available information: ¨ Link counts from SNMP data. ¨ Routing information. (Weights of links) ¨ Additional topological information. ( Peerings, access links) ¨ Assumption on the distribution of demands.

Traffic Matrix Estimation: Existing Techniques and New Directions A. Madina, N. Taft, K. Salamatian, S. Bhattacharyya, C. Diot Sigcomm 2003

Three Existing Techniques n Linear Programming (LP) approach. ¨ n Bayesian estimation. ¨ n O. Goldschmidt - ISMA Workshop 2000 C. Tebaldi, M. West - J. of American Statistical Association, June 1998. Expectation Maximization (EM) approach. ¨ J. Cao, D. Davis, S. Vander Weil, B. Yu - J. of American Statistical Association, 2000.

Terminology n n c=n*(n-1) origin-destination (OD) pairs. X: Traffic matrix. (Xj data transmitted by OD pair j) Y=(y 1, y 2, …, yr ) : vector of link counts. A: r-by-c routing matrix (aij=1, if link i belongs to the path associated to OD pair j) Y=AX r<<c => Infinitely many solutions!

Linear Programming n Objective: n Constraints:

Statistical Approaches

Bayesian Approach Assumes P(Xj) follows a Poisson distribution with mean λj. (independently dist. ) n needs to be estimated. (a prior is needed) n Conditioning on link counts: P(X, Λ|Y) Uses Markov Chain Monte Carlo (MCMC) simulation method to get posterior distributions. n Ultimate goal: compute P(X|Y) n

Expectation Maximization (EM) n Assumes Xj are ind. dist. Gaussian. n Y=AX implies: n Requires a prior for initialization. Incorporates multiple sets of link measurements. Uses EM algorithm to compute MLE. n n

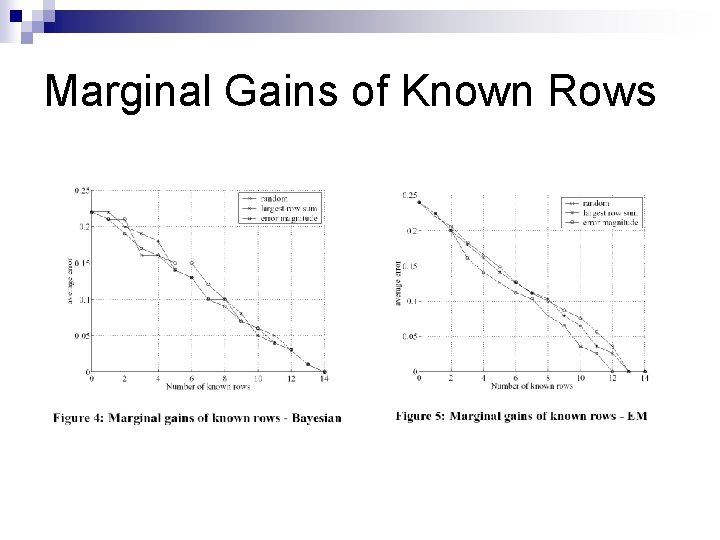
Comparison of Methodologies n n Considers Po. P-Po. P traffic demands. Two different topologies (4 -node, 14 -node). Synthetic TMs. (constant, Poisson, Gaussian, Uniform, Bimodal) Comparison criteria: ¨ Estimation errors yielded. ¨ Sensitivity to prior. ¨ Sensitivity to distribution assumptions.

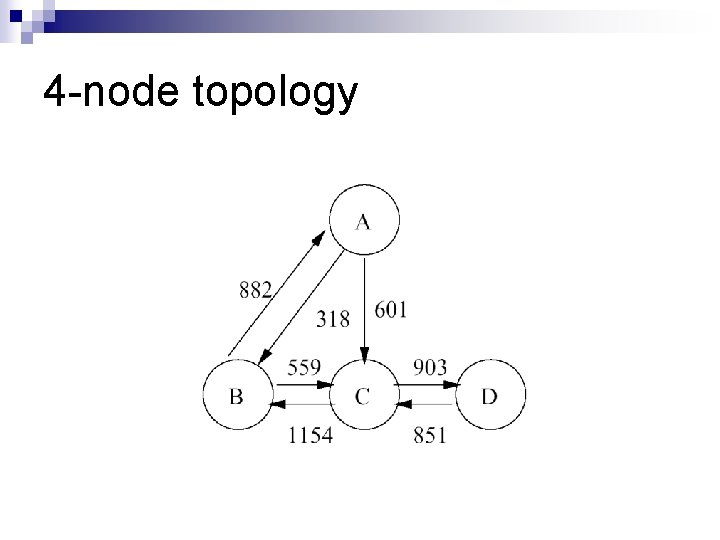
4 -node topology

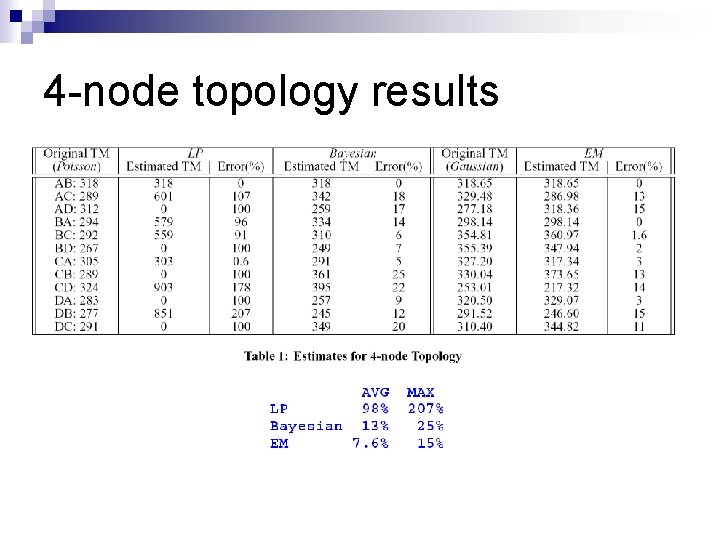
4 -node topology results

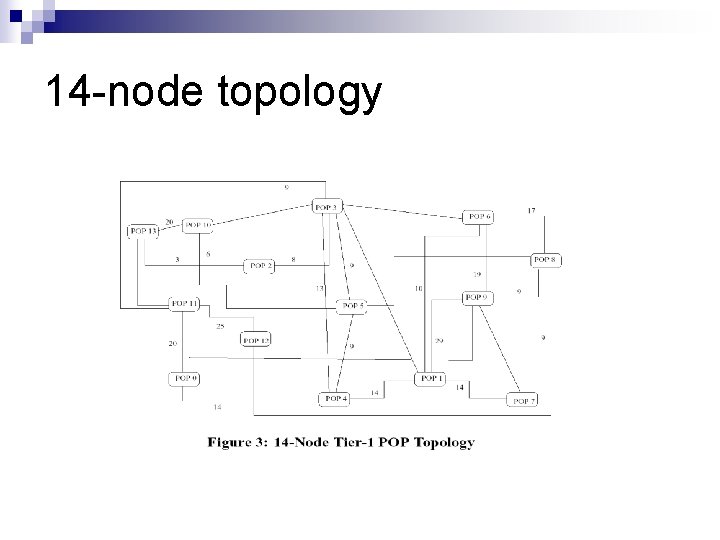
14 -node topology

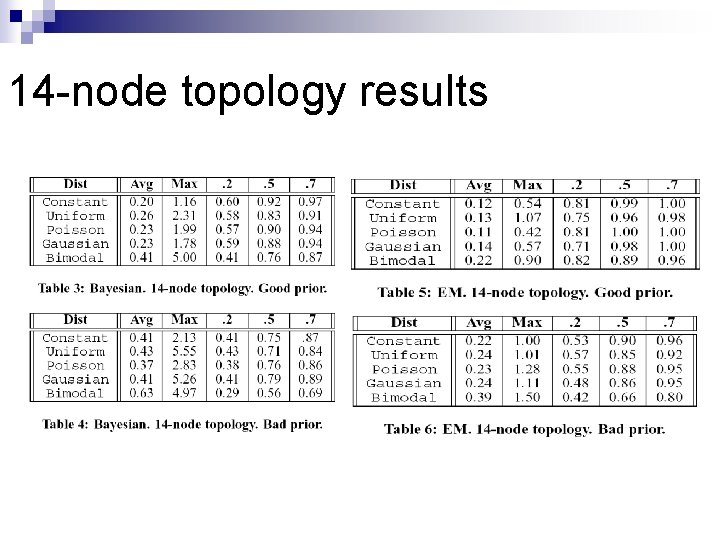
14 -node topology results

Marginal Gains of Known Rows

New Directions n Lessons learned: ¨ Model assumptions do not reflect the true nature of traffic. (multimodal behavior) ¨ Dependence on priors ¨ Link count is not sufficient (Generally more data is available to network operators. ) n Proposed Solutions: ¨ Use choice models to incorporate additional information. ¨ Generate a good prior solution.

New statement of the problem n Xij= Oi. αij ¨ Oi : outflow from node (Po. P) i. ¨ αij : fraction Oi going to Po. P j. Equivalent problem: estimating αij. n Solution via Discrete Choice Models (DCM). ¨ User choices. ¨ ISP choices.

Choice Models n n Decision makers: Po. Ps Set of alternatives: egress Po. Ps. Attributes of decision makers and alternatives: attractiveness (capacity, number of attached customers, peering links). Utility maximization with random utility models.

Random Utility Model Uij= Vij + εij : Utility of Po. P i choosing to send packet to Po. P j. n Choice problem: n Deterministic component: n n Random component: mlogit model used.

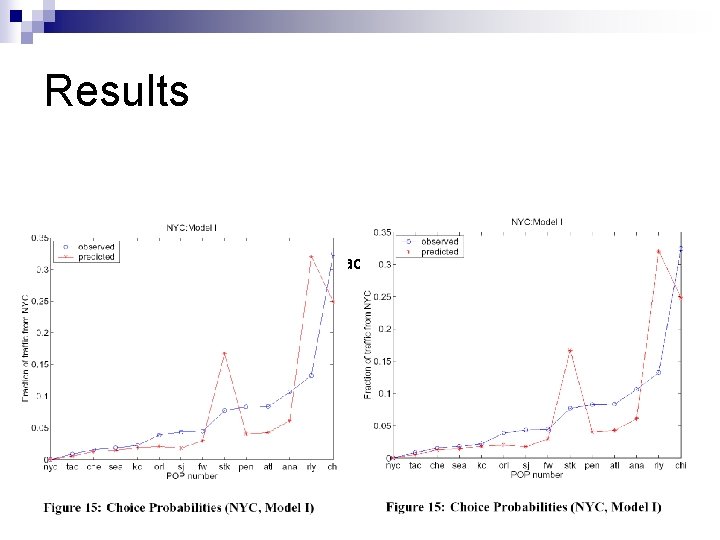
Results Two different models (Model 1: attractiveness, Model 2: attractiveness + repulsion ) n

Fast Accurate Computation of Large -Scale IP Traffic Matrices from Link Loads Y. Zhang, M. Roughan, N. Duffield, A. Greenberg Sigmetrics 2003

Highlights Router to router traffic matrix is computed instead of Po. P to Po. P. n Performance evaluation with real traffic matrices. n Tomogravity method (Gravity + Tomography) n

Tomogravity n Two step modeling. ¨ Gravity Model: Initial solution obtained using edge link load data and ISP routing policy. ¨ Tomographic Estimation: Initial solution is refined by applying quadratic programming to minimize distance to initial solution subject to tomographic constraints (link counts).

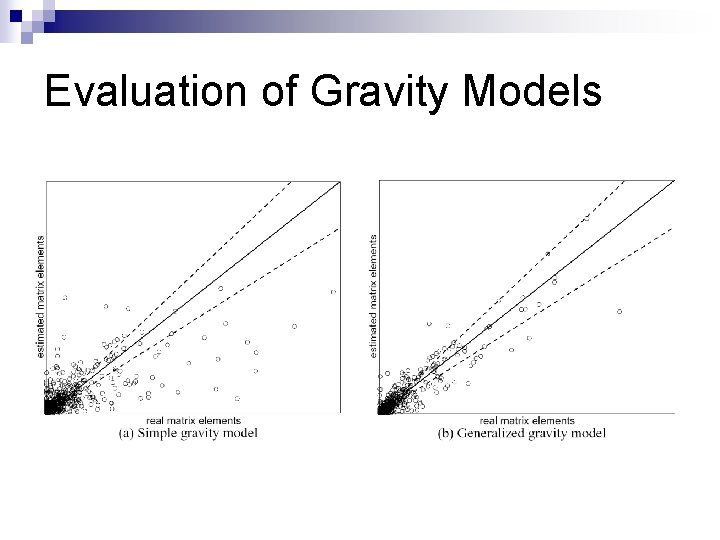
Gravity Modeling n General formula: n Simple gravity model: Try to estimate the amount of traffic between edge links.

Generalized Gravity Model n Four traffic categories ¨ Transit ¨ Outbound ¨ Internal n n n Peers: P 1, P 2, … Access links: a 1, a 2, . . . Peering links: p 1, p 2, …

Generalized Gravity Model

Generalized Gravity Model

Tomography n Solution should be consistent with the link counts.

Reducing the computational complexity Hundreds of backbone routers, ten thousands of unknowns. n Observations: n Some elements of the BR to BR matrix are empty. (Multiple BRs in each Po. P, shortest paths) n Topological equivalence. (Reduce the number of IGP simulations) n

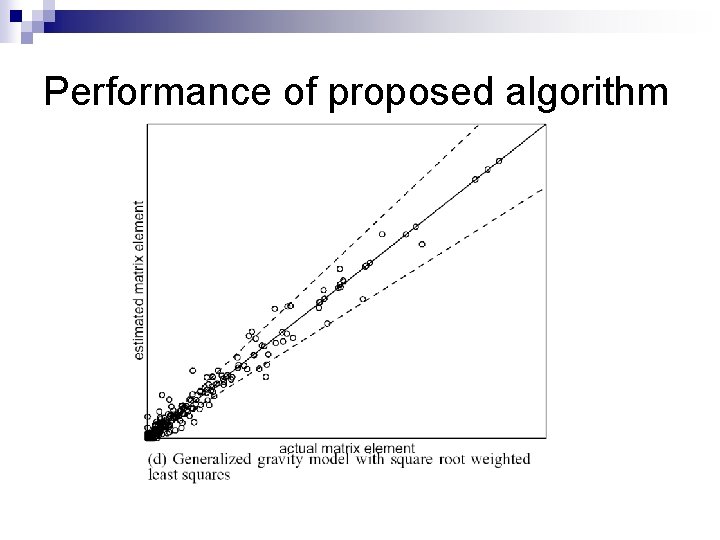
Quadratic Programming n Problem Definition: Use SVD to solve the inverse problem. n Use Iterative Proportional Fitting (IPF) to ensure non-negativity. n

Evaluation of Gravity Models

Performance of proposed algorithm

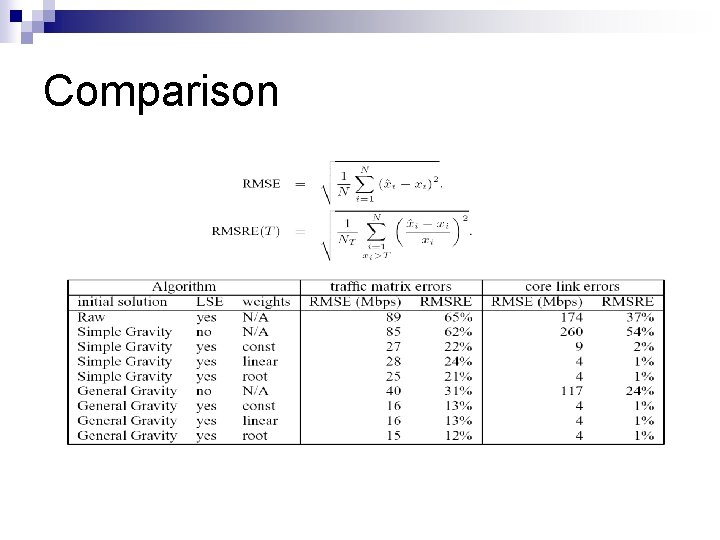
Comparison

Robustness Measurement errors x=At+ε ε=x*N(0, σ) n

Questions?