Todays Topics Weight Space for ANNs Gradient Descent

Today’s Topics • • • Weight Space (for ANNs) Gradient Descent and Local Minima Stochastic Gradient Descent Backpropagation The Need to Train the Biases and a Simple Algebraic Trick • Perceptron Training Rule and a Worked Example • Case Analysis of Delta Rule 11/10/16 cs 540 - Fall 2016 (Shavlik©), Lecture 18, Week 10 1

WARNING! Some Calculus Ahead 11/10/16 cs 540 - Fall 2016 (Shavlik©), Lecture 18, Week 10 2

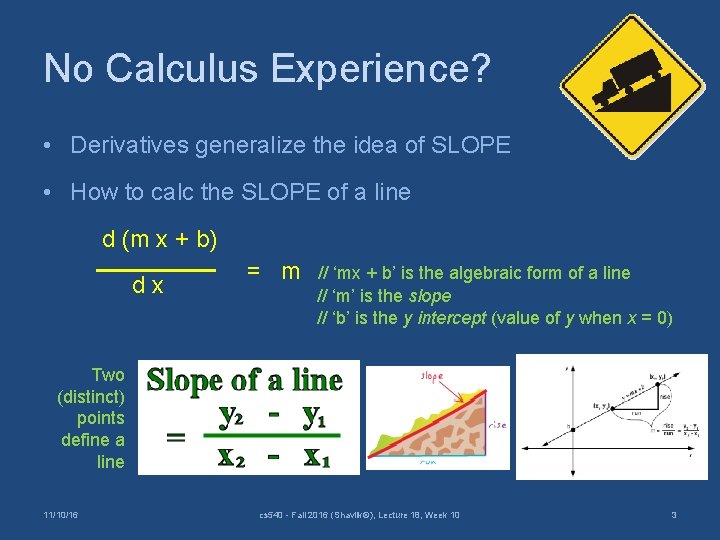
No Calculus Experience? • Derivatives generalize the idea of SLOPE • How to calc the SLOPE of a line d (m x + b) dx = m // ‘mx + b’ is the algebraic form of a line // ‘m’ is the slope // ‘b’ is the y intercept (value of y when x = 0) Two (distinct) points define a line 11/10/16 cs 540 - Fall 2016 (Shavlik©), Lecture 18, Week 10 3

Weight Space • Given a neural-network layout, the weights and biases are free parameters that define a space • Each point in this Weight Space specifies a network weight space is a continuous space we search • Associated with each point is an error rate, E, over the training data • Backprop performs gradient descent in weight space 11/10/16 cs 540 - Fall 2016 (Shavlik©), Lecture 18, Week 10 4

Gradient Descent in Weight Space Total Error on Training Set ERROR with Current Wgt Settings ∂E ∂W W 1 W 2 11/10/16 New Wgt Settings cs 540 - Fall 2016 (Shavlik©), Lecture 18, Week 10 W 1 Current Wgt Settings W 2 5

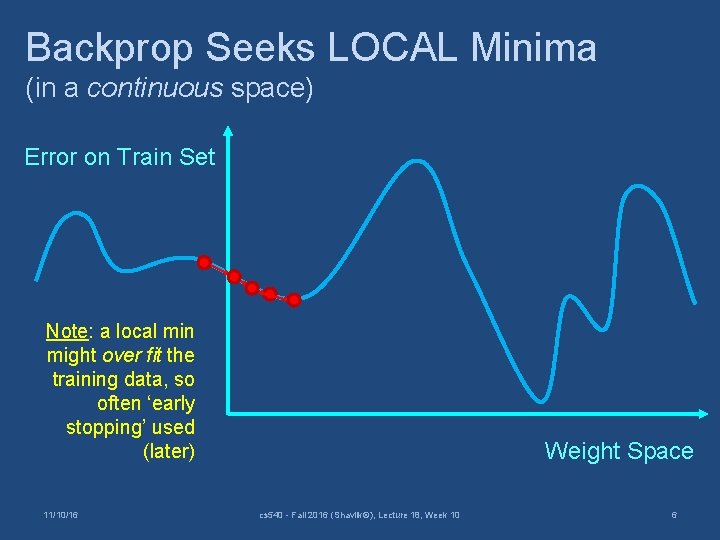
Backprop Seeks LOCAL Minima (in a continuous space) Error on Train Set Note: a local min might over fit the training data, so often ‘early stopping’ used (later) 11/10/16 Weight Space cs 540 - Fall 2016 (Shavlik©), Lecture 18, Week 10 6

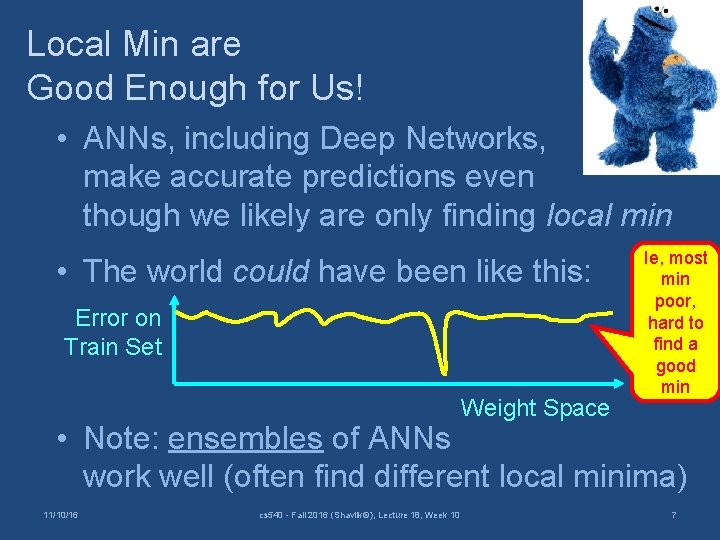
Local Min are Good Enough for Us! • ANNs, including Deep Networks, make accurate predictions even though we likely are only finding local min • The world could have been like this: Error on Train Set Weight Space Ie, most min poor, hard to find a good min • Note: ensembles of ANNs work well (often find different local minima) 11/10/16 cs 540 - Fall 2016 (Shavlik©), Lecture 18, Week 10 7

The Gradient-Descent Rule E(w) [ The ‘gradient’ E, w 0 E, w 1 E , w 2 …, E_ w. N ] This is a N+1 dimensional vector (ie, the ‘slope’ in weight space) Since we want to reduce errors, we want to go ‘down hill’ We’ll take a finite step in weight space: E E w = - E ( w ) ‘delta’ = the change to w 11/10/16 or wi = - E wi cs 540 - Fall 2016 (Shavlik©), Lecture 18, Week 10 W 1 W 2 w 8

‘On Line’ vs. ‘Batch’ Backprop • Technically, we should look at the error gradient for the entire training set, before taking a step in weight space (‘batch’ backprop) • However, in practice we take a step after each example (‘on-line’ backprop) – Much faster convergence (learn after each example) – Called ‘stochastic’ gradient descent – Stochastic gradient descent quite popular at Google, Facebook, Microsoft, etc due to easy parallelism 11/10/16 cs 540 - Fall 2016 (Shavlik©), Lecture 18, Week 10 9

‘On Line’ vs. ‘Batch’ BP (continued) * Note wi, BATCH wi, ON-LINE, for i > 1 E BATCH – add w vectors for every training example, then ‘move’ in weight space wex 1 wi wex 3 w E ON-LINE – ‘move’ after each example (aka, stochastic gradient descent) wex 2 wex 1 Vector from BATCH wex 3 w * Final locations in w space need not be the same for BATCH and ON-LINE 11/10/16 cs 540 - Fall 2016 (Shavlik©), Lecture 18, Week 10 10

BP Calculations (note: text uses ‘loss’ instead of ‘error’) k j i Assume one layer of hidden units (std. non-deep topology) 1. Error ½ ( Teacheri – Output i ) 2 2. = ½ (Teacheri – F ( [ Wi, j x Output j ] )2 3. = ½ (Teacheri – F ( [ Wi, j x F ( Wj, k x Output k)] ))2 Determine ∂ Error = ∂ Wi, j (use equation 2) ∂ Error ∂ Wj, k = (use equation 3) Recall 11/10/16 See text’s Section 18. 7. 4 for the specific calculations wx, y = - (∂ E / ∂ wx, y ) cs 540 - Fall 2016 (Shavlik©), Lecture 18, Week 10 11

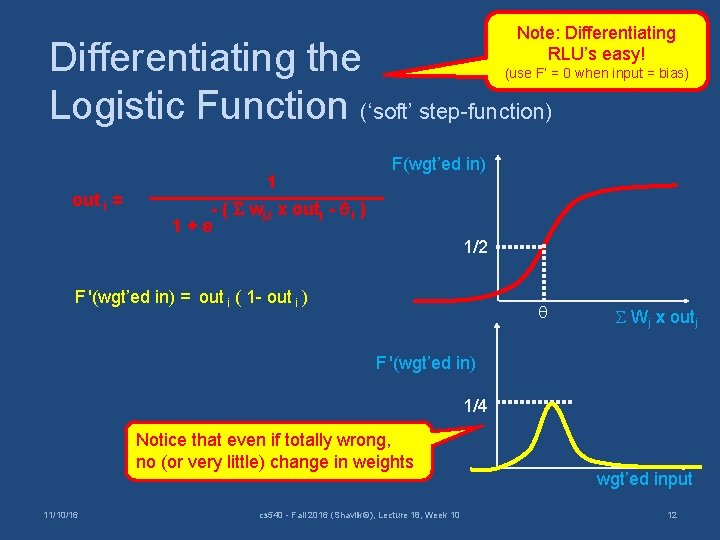
Note: Differentiating RLU’s easy! Differentiating the Logistic Function (‘soft’ step-function) (use F’ = 0 when input = bias) out i = 1 F(wgt’ed in) - ( wj, i x outj - i ) 1+e 1/2 F '(wgt’ed in) = out i ( 1 - out i ) Wj x outj F '(wgt’ed in) 1/4 Notice that even if totally wrong, no (or very little) change in weights 11/10/16 cs 540 - Fall 2016 (Shavlik©), Lecture 18, Week 10 wgt’ed input 12

Gradient Descent for the Perceptron (for the simple case of linear output units) 2 Error ½ ( T – o ) ∂E ∂ Wk 11/10/16 Network’s output Teacher’s answer (a constant wrt the weights) = (T – o) ∂ (T – o) = - (T – o) ∂ o ∂ Wk cs 540 - Fall 2016 (Shavlik©), Lecture 18, Week 10 13

Continuation of Derivation ∂E ∂ Wk = - (T – o) ∂( ∑ w j x j) ∂ Wk = - (T – o) x k So Stick in formula for output ΔWk = η (T – o) xk Recall ΔWk - η ∂ Wk The Perceptron Rule We’ll use for both LINEAR and STEP-FUNCTION activation 11/10/16 ∂E cs 540 - Fall 2016 (Shavlik©), Lecture 18, Week 10 Also known as the delta rule and other names (with some variation in the calculation) 14

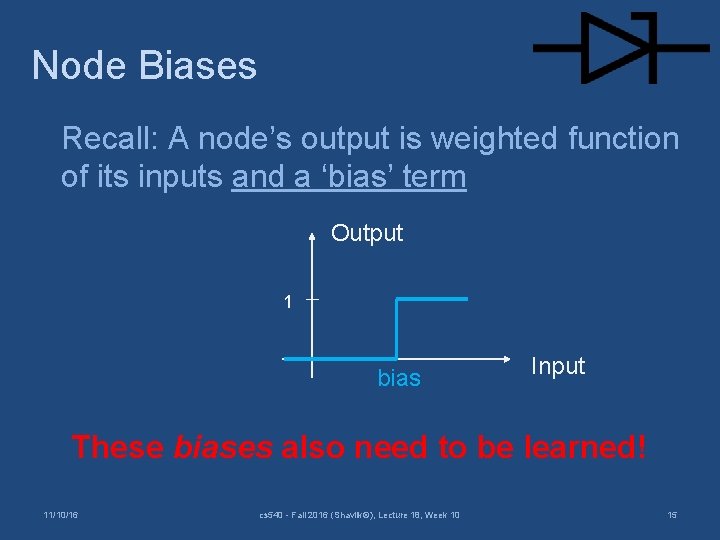
Node Biases Recall: A node’s output is weighted function of its inputs and a ‘bias’ term Output 1 bias Input These biases also need to be learned! 11/10/16 cs 540 - Fall 2016 (Shavlik©), Lecture 18, Week 10 15

Training Biases ( Θ’s ) A node’s output (assume ‘step function’ for simplicity) 1 if W 1 X 1 + W 2 X 2 +…+ Wn Xn ≥ Θ 0 otherwise Rewriting W 1 X 1 + W 2 X 2 + … + W n Xn – Θ ≥ 0 W 1 X 1 + W 2 X 2 + … + Wn Xn + Θ (-1) ≥ 0 ‘activation’ weight 11/10/16 cs 540 - Fall 2016 (Shavlik©), Lecture 18, Week 10 16

Training Biases (cont. ) Hence, add another unit whose activation is always -1 The bias is then just another weight! Eg Θ -1 11/10/16 cs 540 - Fall 2016 (Shavlik©), Lecture 18, Week 10 Θ 17

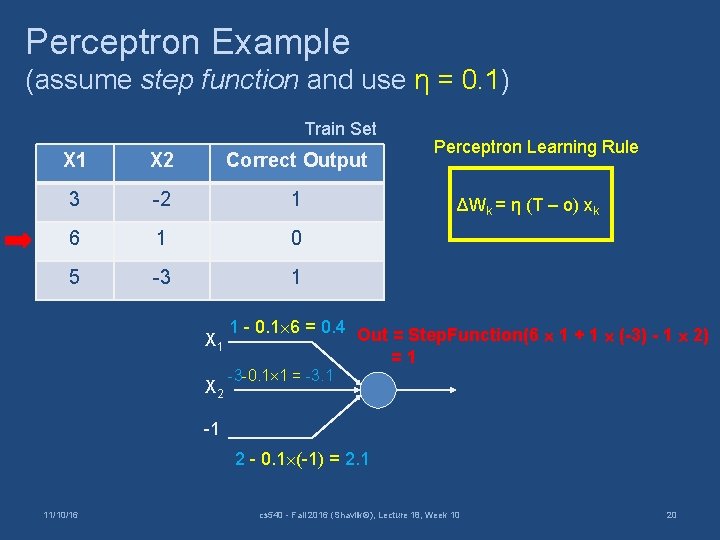
Perceptron Example (assume step function and use η = 0. 1) Train Set X 1 X 2 Correct Output 3 -2 1 6 1 0 5 -3 1 X 2 -1 11/10/16 1 -3 Perceptron Learning Rule ΔWk = η (T – o) xk Out = Step. Function(3 1 - 2 (-3) - 1 2) =1 2 No wgt changes, since correct cs 540 - Fall 2016 (Shavlik©), Lecture 18, Week 10 18

Perceptron Example (assume step function and use η = 0. 1) Train Set X 1 X 2 Correct Output 3 -2 1 6 1 0 5 -3 1 X 2 -1 11/10/16 1 Perceptron Learning Rule ΔWa = η (T – o) xa Out = Step. Function(6 1 + 1 (-3) - 1 2) = 1 // So need to update weights -3 2 cs 540 - Fall 2016 (Shavlik©), Lecture 18, Week 10 19

Perceptron Example (assume step function and use η = 0. 1) Train Set X 1 X 2 Correct Output 3 -2 1 6 1 0 5 -3 1 X 2 Perceptron Learning Rule ΔWk = η (T – o) xk 1 - 0. 1 6 = 0. 4 Out = Step. Function(6 1 + 1 (-3) - 1 2) =1 -3 -0. 1 1 = -3. 1 -1 2 - 0. 1 (-1) = 2. 1 11/10/16 cs 540 - Fall 2016 (Shavlik©), Lecture 18, Week 10 20

Pushing the Weights and Bias in the Correct Direction when Wrong Output Assume TEACHER=1 and ANN=0, so some combo of (a) wgts on some positively valued inputs too small (b) wgts on some negatively valued inputs too large (c) ‘bias’ too large Opposite movement when TEACHER= 0 and ANN = 1 Wgt’ed Sum bias 11/10/16 cs 540 - Fall 2016 (Shavlik©), Lecture 18, Week 10 21

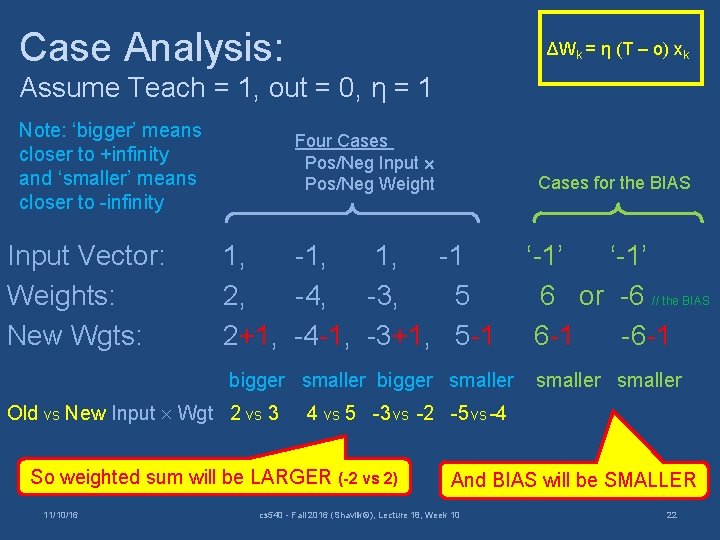
Case Analysis: ΔWk = η (T – o) xk Assume Teach = 1, out = 0, η = 1 Note: ‘bigger’ means closer to +infinity and ‘smaller’ means closer to -infinity Input Vector: Weights: New Wgts: Four Cases Pos/Neg Input Pos/Neg Weight Cases for the BIAS 1, -1, 1, -1 2, -4, -3, 5 2+1, -4 -1, -3+1, 5 -1 bigger smaller Old vs New Input Wgt 2 vs 3 smaller 4 vs 5 -3 vs -2 -5 vs -4 So weighted sum will be LARGER (-2 vs 2) 11/10/16 ‘-1’ 6 or -6 // the BIAS 6 -1 -6 -1 And BIAS will be SMALLER cs 540 - Fall 2016 (Shavlik©), Lecture 18, Week 10 22

HW 4 • Train a perceptron on WINE – For N Boolean-valued features, have N+1 input units (+1 due to “-1” input) and 1 output unit – Learned model rep’ed by vector of N+1 doubles – Your code should handle any dataset that meets HW 0 spec • (Maybe also train an ANN with 100 HU’s - but not required) • Employ ‘early stopping’ (later) • Compare perceptron testset results to random forests 11/10/16 cs 540 - Fall 2016 (Shavlik©), Lecture 18, Week 10 23

Wrapup of Basics of ANN Training ∂ Error ∂ Wk • We differentiate (in the calculus sense) all the free parameters in an ANN with a fixed structure (‘topology’) – If all else is held constant (‘partial derivatives’), what is the impact of changing weightk? – Simultaneously move each weight a small amount in the direction that reduces error – Process example-by-example, many times • Seeks local minimum, ie, where all derivatives = 0 11/10/16 cs 540 - Fall 2016 (Shavlik©), Lecture 18, Week 10 24