Intelligent CS 5 Todays Lab MZ Chess is

Intelligent CS 5 ? Today’s Lab: M-Z Chess is the Drosophila of artificial intelligence. - Alexander Kronrod Games: computers vs. humans… • HW 11 (1 problem !) Recitation for HW 11 -- Friday 11/12, 8: 00 am The computer that defeated Garry Kasparov 1997 due Sunday, 11/14 at midnight due Monday, 11/15 at midnight M/T sections W/Th sections • 2 nd midterm exam -- this Friday, 11/12 exemption: > 95% HW Take-home, 2. 0 hours, closed-book exam. Practice problems are online… www. cs. hmc. edu/~dodds/cs 5 (top link) Exam will be available this Friday; it’s due Sunday evening by 5: 00 pm.

Two-player games • Strategic thinking was considered essential for intelligence • Computer Chess has a long history: Ranking 500 beginner early programs ~ 1960’s amateur 1200 Mac. Hack (1100) ~ 1967 MIT world ranked 2000 Slate (2070) ~ 1970’s Northwestern Deep Thought ~ 1989 Carnegie Mellon Deep Blue ~ 1996 2800 IBM world champion Deep Blue rematch ~ 1997 IBM

Computers’ strategy… • Strategic thinking was considered essential for intelligence • Computer Chess has a long history: Ranking 500 beginner early programs ~ 1960’s 100’s of moves/sec amateur 1200 Mac. Hack (1100) ~ 1967 MIT 10, 000’s of moves/sec 100, 000 moves/sec 200, 000 moves/sec world ranked 2000 Slate (2070) ~ 1970’s Northwestern Deep Thought ~ 1989 Carnegie Mellon how far ahead is this? Deep Blue ~ 1996 2800 IBM world champion Deep Blue rematch ~ 1997 IBM

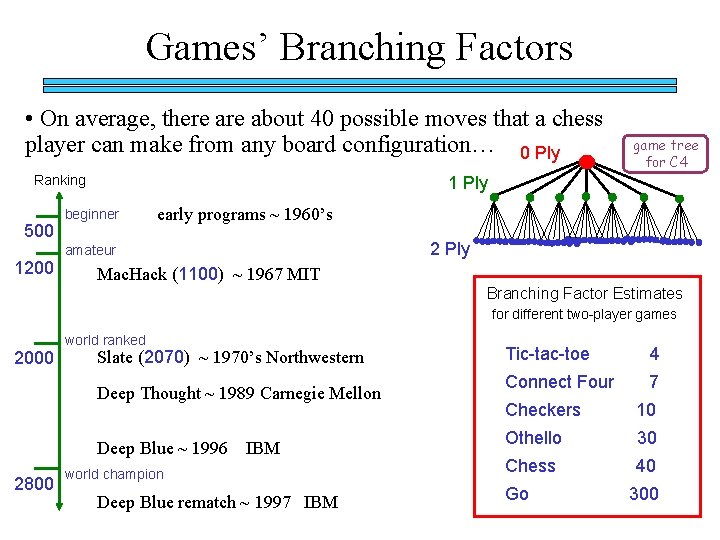
Games’ Branching Factors • On average, there about 40 possible moves that a chess player can make from any board configuration… 0 Ply Ranking 500 1 Ply beginner early programs ~ 1960’s 2 Ply amateur 1200 game tree for C 4 Mac. Hack (1100) ~ 1967 MIT Branching Factor Estimates for different two-player games world ranked 2000 Slate (2070) ~ 1970’s Northwestern Deep Thought ~ 1989 Carnegie Mellon Deep Blue ~ 1996 2800 IBM world champion Deep Blue rematch ~ 1997 IBM Tic-tac-toe 4 Connect Four 7 Checkers 10 Othello 30 Chess 40 Go 300

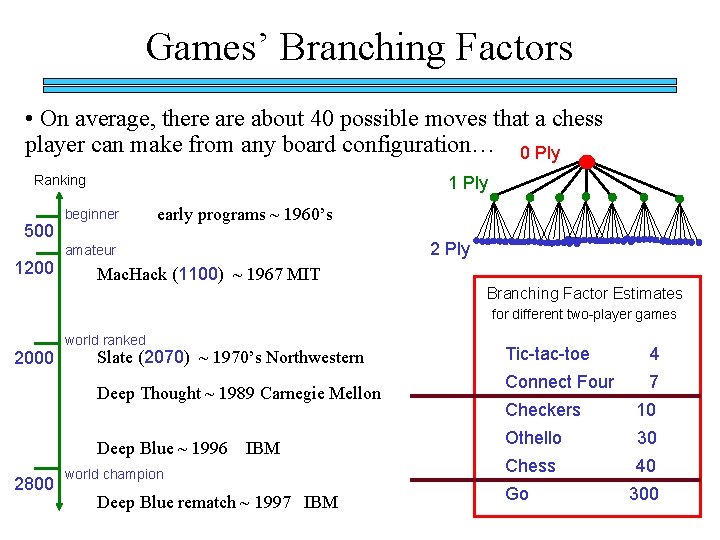
Games’ Branching Factors • On average, there about 40 possible moves that a chess player can make from any board configuration… 0 Ply Ranking 500 1 Ply beginner early programs ~ 1960’s 2 Ply amateur 1200 Mac. Hack (1100) ~ 1967 MIT Branching Factor Estimates for different two-player games world ranked 2000 Slate (2070) ~ 1970’s Northwestern Deep Thought ~ 1989 Carnegie Mellon Deep Blue ~ 1996 2800 IBM world champion Deep Blue rematch ~ 1997 IBM Tic-tac-toe 4 Connect Four 7 Checkers 10 Othello 30 Chess 40 Go 300

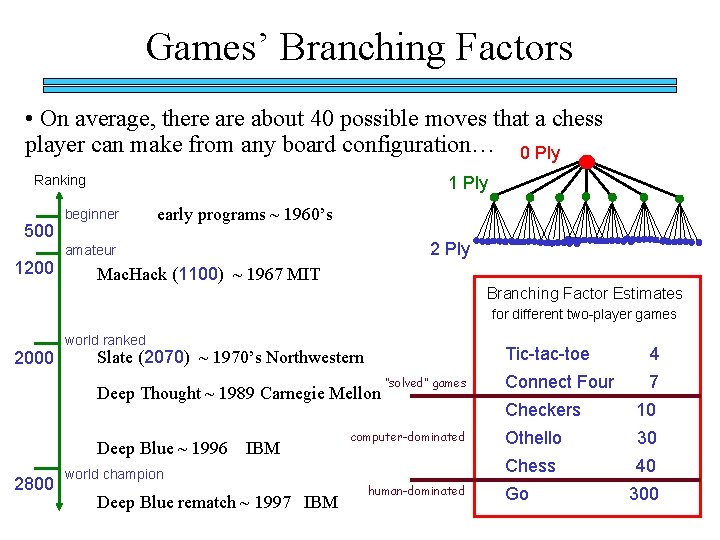
Games’ Branching Factors • On average, there about 40 possible moves that a chess player can make from any board configuration… 0 Ply Ranking 500 1 Ply beginner early programs ~ 1960’s 2 Ply amateur 1200 Mac. Hack (1100) ~ 1967 MIT Branching Factor Estimates for different two-player games world ranked 2000 Slate (2070) ~ 1970’s Northwestern Deep Thought ~ 1989 Carnegie Mellon Deep Blue ~ 1996 2800 IBM world champion Deep Blue rematch ~ 1997 IBM “solved” games computer-dominated human-dominated Tic-tac-toe 4 Connect Four 7 Checkers 10 Othello 30 Chess 40 Go 300

Winning: Details public boolean wins. For(char ch) { for (int r=0 ; r<this. nrows-3 ; ++r) { for (int c=0 ; c<this. ncols-3 ; ++c) { if (this. data[r+0][c+0] == ch && this. data[r+1][c+1] == ch && this. data[r+2][c+2] == ch && this. data[r+3][c+3] == ch) { return true; } } } … same idea for vert. , horiz. , other diag. … } return false; which diagonals? which board piece? which curly braces?

Winning: Details (compact version) public boolean wins. For(char ch) { for (int r=0 ; r<this. n. Rows-3 ; ++r) for (int c=0 ; c<this. n. Cols-3 ; ++c) if (this. data[r+0][c+0] == ch && this. data[r+1][c+1] == ch && this. data[r+2][c+2] == ch && this. data[r+3][c+3] == ch) return true; … same idea for vert. , horiz. , other diag. … } return false;

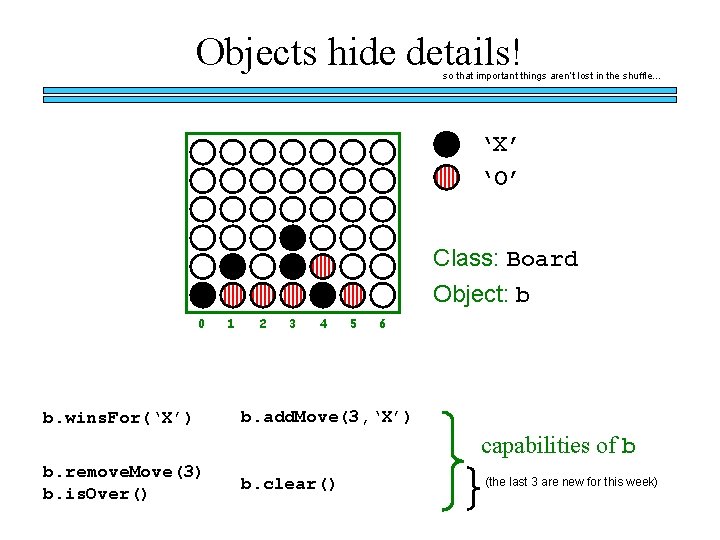
Objects hide details! so that important things aren’t lost in the shuffle… ‘X’ ‘O’ Class: Board Object: b 0 b. wins. For(‘X’) 1 2 3 4 5 6 b. add. Move(3, ‘X’) capabilities of b b. remove. Move(3) b. is. Over() b. clear() (the last 3 are new for this week)

Hw 10 Hw 11 class CS 5 App { public static void main(String[] args) { H. pl("Hi! Welcome to Connect 4. . . "); H. pl("How many rows/columns ? (4 -15)"); int R = H. ni(); int C = H. ni(); Board b = new Board(R, C); char player = 'X'; while (true) { b. print(); int c = H. ni(); // gets next move b. add. Move(c, player); if (b. wins. For(player)) break; if (player == 'X') player = '0'; else player = 'X'; } // end of while } } Objects hide details!

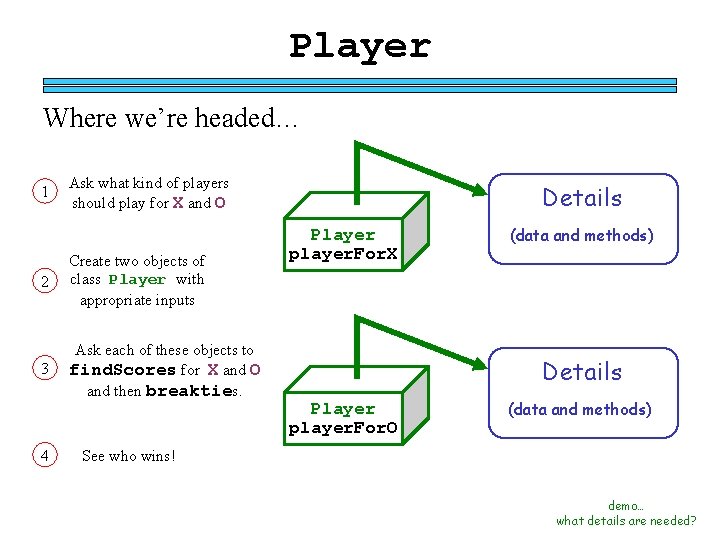
Player Where we’re headed… 1 Ask what kind of players should play for X and O 2 Create two objects of class Player with appropriate inputs 3 Ask each of these objects to find. Scores for X and O and then breakties. 4 Details Player player. For. X (data and methods) Details Player player. For. O (data and methods) See who wins! demo… what details are needed?

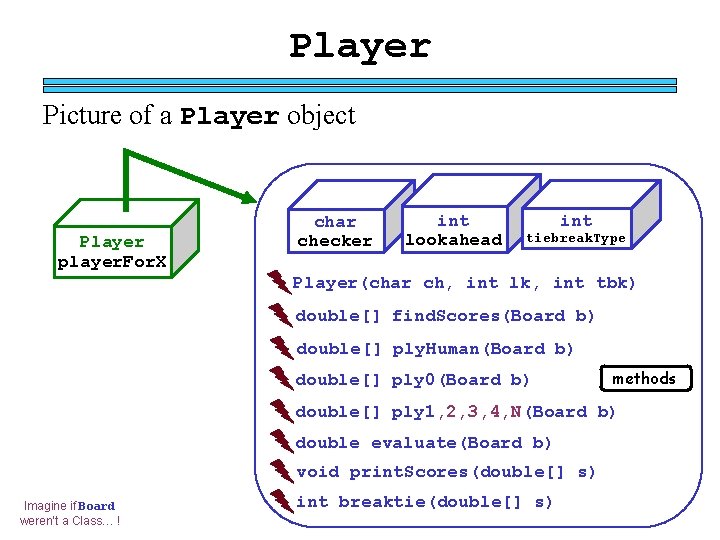
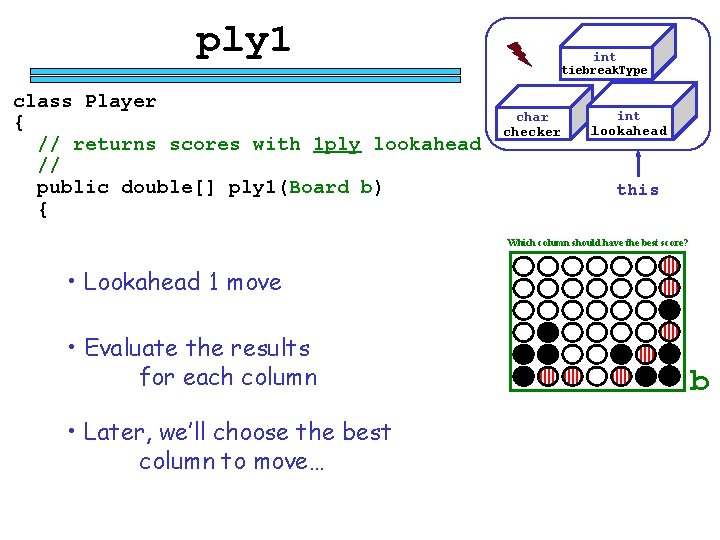
Player Picture of a Player object Player player. For. X char checker int lookahead int tiebreak. Type Player(char ch, int lk, int tbk) double[] find. Scores(Board b) double[] ply. Human(Board b) double[] ply 0(Board b) methods double[] ply 1, 2, 3, 4, N(Board b) double evaluate(Board b) void print. Scores(double[] s) Imagine if Board weren’t a Class… ! int breaktie(double[] s)

class Player { private char checker; private int lookahead; private int tiebreak. Type; Player code public Player(char ch, int la, int tbk) { // constructor } public char get. Checker() // accessor “getter” method { } public char me() { // short for get. Checker() } public char opp() { } // returns the opponent’s checker

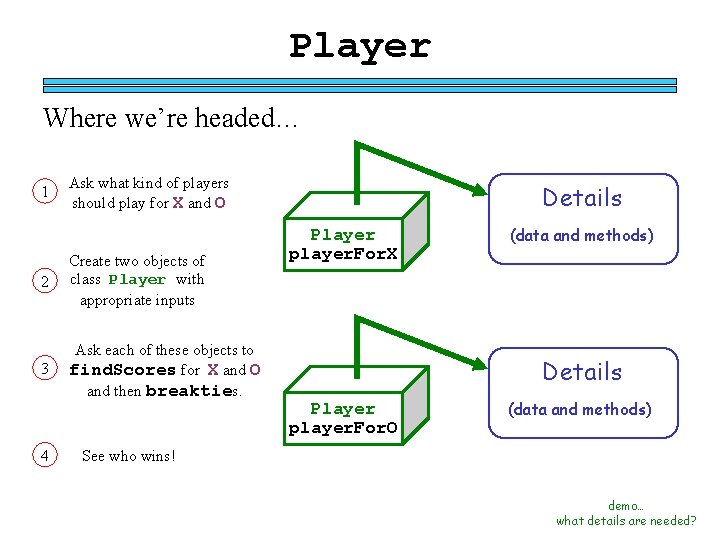
Player Where we’re headed… 1 Ask what kind of players should play for X and O 2 Create two objects of class Player with appropriate inputs 3 Ask each of these objects to find. Scores for X and O and then breakties. 4 Details Player player. For. X (data and methods) Details Player player. For. O (data and methods) See who wins! demo… what details are needed?

Hw 10 class CS 5 App { public static void main(String[] args) { H. pl("Hi! Welcome to Connect 4. . . "); int R = H. ni(); int C = H. ni(); Board b = new Board(R, C); char player = 'X'; while (true) { b. print(); int uc = H. ni(); // user’s column b. add. Move(uc, player); if (b. wins. For(player)) break; if (player == 'X') player = '0'; else player = 'X'; } // end of while } } Hw 11

Choosing a move 1) Find scores at appropriate lookahead… ply 0: 0 ply of lookahead ply 1: 1 ply of lookahead ply 2, 3, 4: 2, 3, 4 ply of lookahead ply. Human: ask the user find. Scores chooses one of these methods to run 2) Print the scores. print. Scores: prints the scores to each column 3) Break ties to determine the next move. breaktie: chooses ONE maximum score

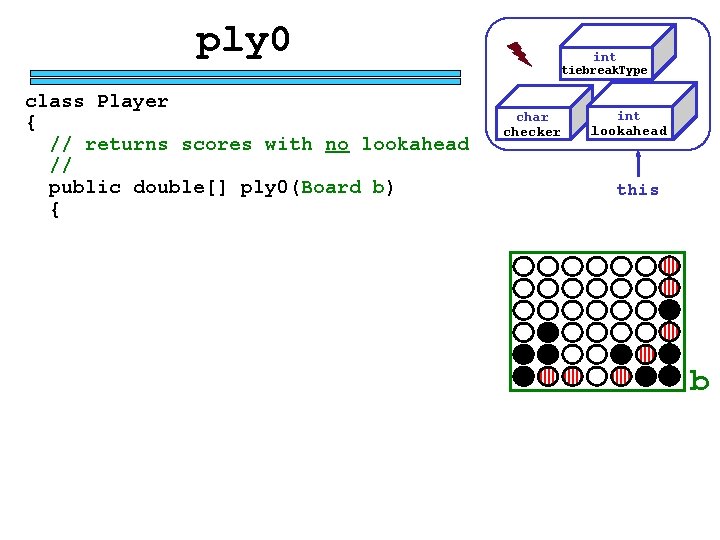
ply 0 int tiebreak. Type class Player { // returns scores with no lookahead // public double[] ply 0(Board b) { char checker int lookahead this b

ply 1 int tiebreak. Type class Player { // returns scores with 1 ply lookahead // public double[] ply 1(Board b) { char checker int lookahead this Which column should have the best score? • Lookahead 1 move • Evaluate the results for each column • Later, we’ll choose the best column to move… b

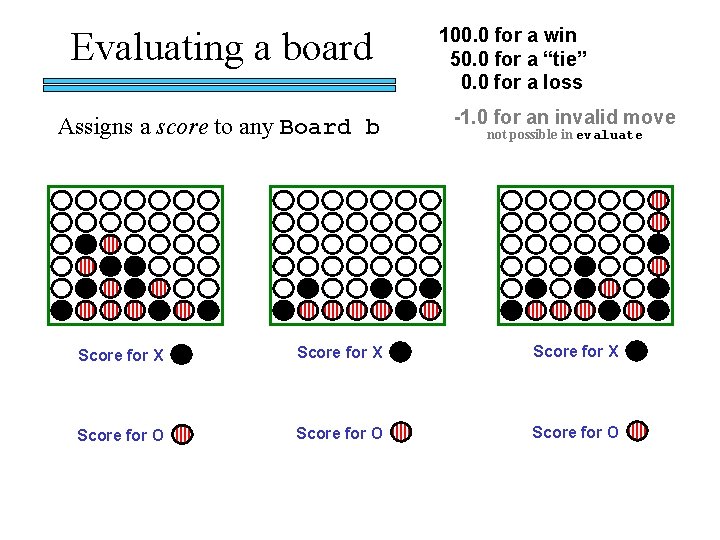
Evaluating a board Assigns a score to any Board b 100. 0 for a win 50. 0 for a “tie” 0. 0 for a loss -1. 0 for an invalid move not possible in evaluate Score for X Score for O

evaluate 100. 0 for a win 50. 0 for a “tie” 0. 0 for a loss -1. 0 for an invalid move class Player { // returns the appropriate score for b // remember: all of Player’s methods are available public double evaluate(Board b) { Improvements? Write tournament. Evaluate for Ex. Cr. !

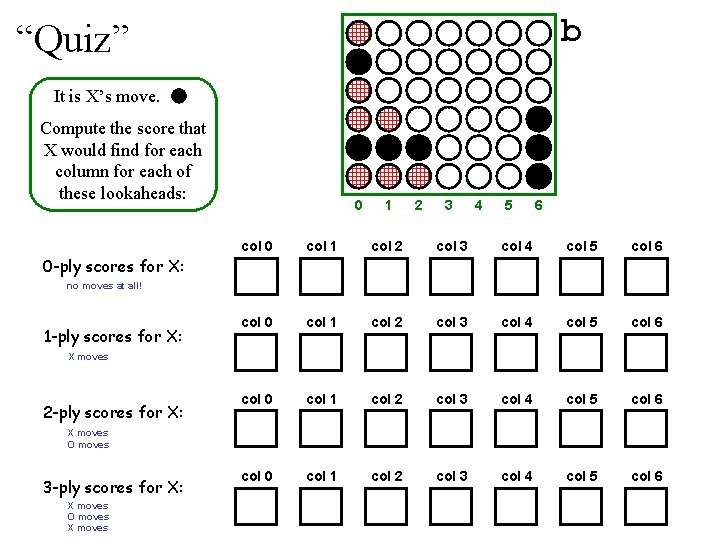
b “Quiz” It is X’s move. . Compute the score that X would find for each column for each of these lookaheads: 0 1 2 3 4 5 6 col 0 col 1 col 2 col 3 col 4 col 5 col 6 0 -ply scores for X: no moves at all! 1 -ply scores for X: X moves 2 -ply scores for X: X moves O moves 3 -ply scores for X: X moves O moves X moves

Write breaktie to return a randomly chosen best score (max score) from an array of scores named s. class Player { private int tiebreak. Type; private int lookahead; private char checker; public int breaktie(double[] s) { double max. Score = get. Max(s); /* assume get. Max is already written */ if (this. tiebreak. Type == 2) */ { } } } /* random tie breaker is tiebreak. Type == 2

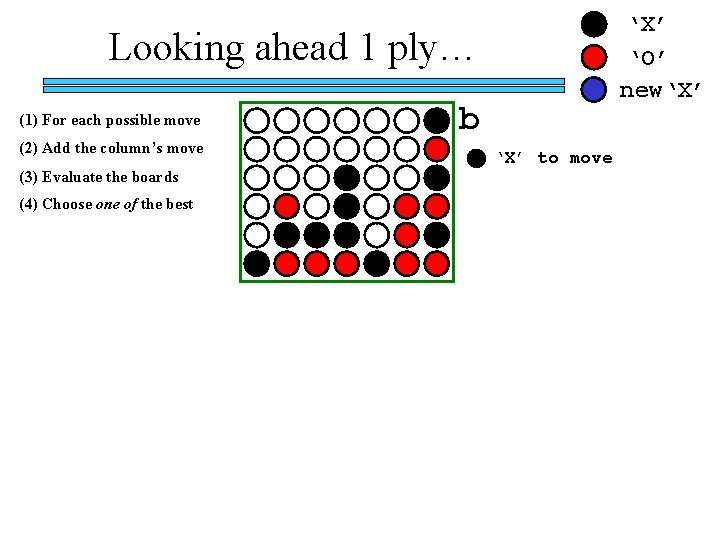
‘X’ ‘O’ new‘X’ Looking ahead 1 ply… (1) For each possible move (2) Add the column’s move (3) Evaluate the boards (4) Choose one of the best b ‘X’ to move

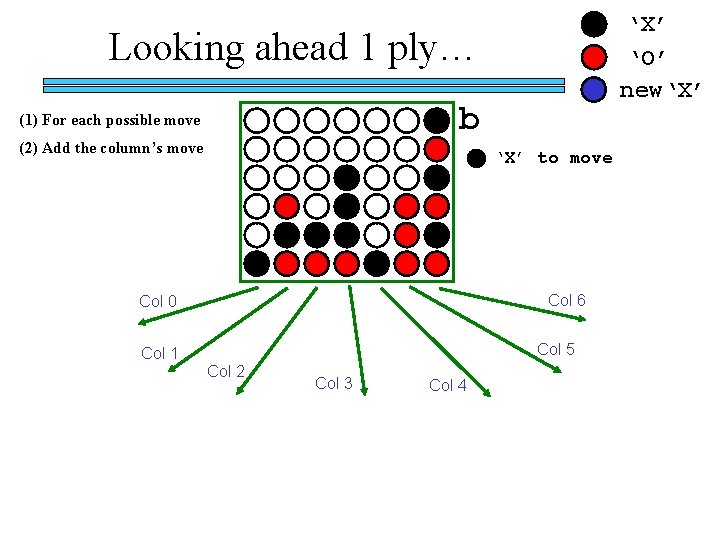
‘X’ ‘O’ new‘X’ Looking ahead 1 ply… b (1) For each possible move (2) Add the column’s move ‘X’ to move Col 6 Col 0 Col 5 Col 1 Col 2 Col 3 Col 4

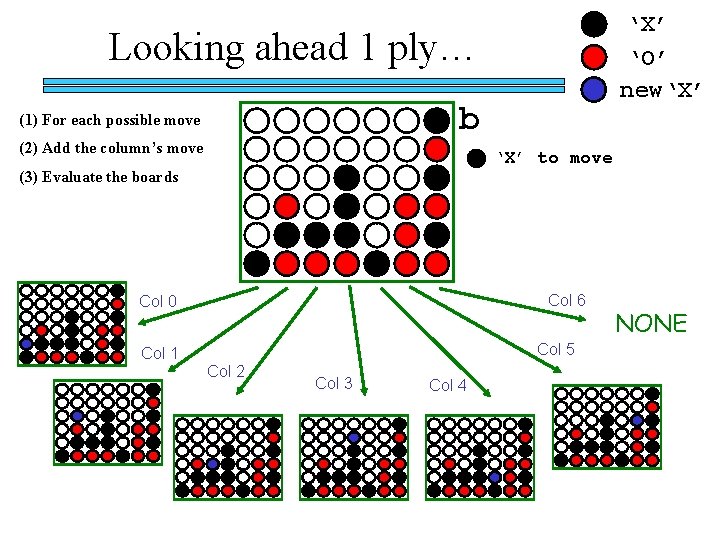
‘X’ ‘O’ new‘X’ Looking ahead 1 ply… b (1) For each possible move (2) Add the column’s move ‘X’ to move (3) Evaluate the boards Col 6 Col 0 Col 5 Col 1 Col 2 Col 3 Col 4 NONE

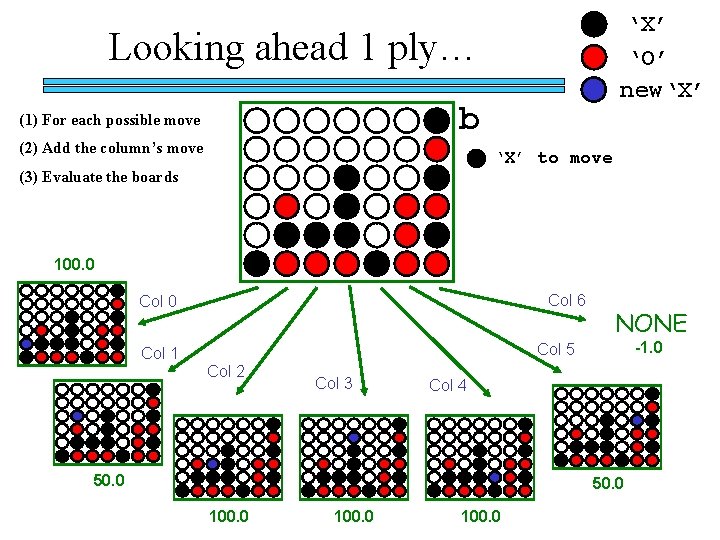
‘X’ ‘O’ new‘X’ Looking ahead 1 ply… b (1) For each possible move (2) Add the column’s move ‘X’ to move (3) Evaluate the boards 100. 0 Col 6 Col 0 NONE -1. 0 Col 5 Col 1 Col 2 Col 3 Col 4 50. 0 100. 0

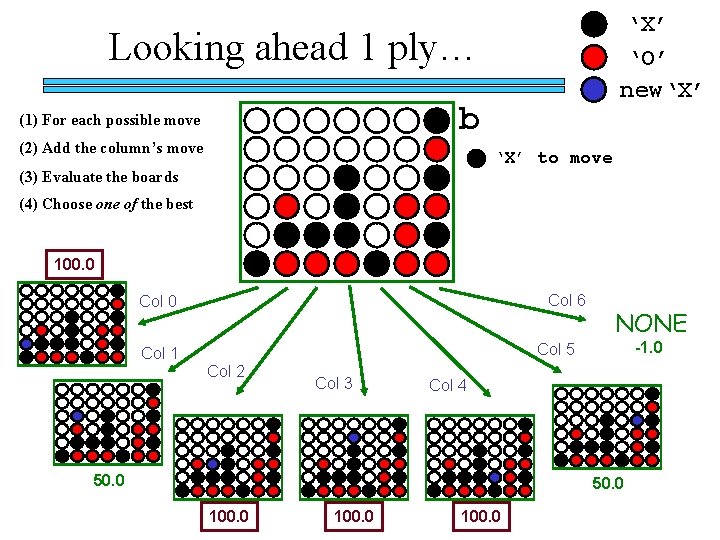
‘X’ ‘O’ new‘X’ Looking ahead 1 ply… b (1) For each possible move (2) Add the column’s move ‘X’ to move (3) Evaluate the boards (4) Choose one of the best 100. 0 Col 6 Col 0 NONE -1. 0 Col 5 Col 1 Col 2 Col 3 Col 4 50. 0 100. 0

public double[] ply 1(Board b) { ply 1

? Strategic thinking = intelligence Two-player games have been a key focus of AI as long as computers have been around… Humans and computers have different relative strengths in these games:

? Strategic thinking = intelligence Two-player games have been a key focus of AI as long as computers have been around… Humans and computers have different relative strengths in these games: computers good at looking ahead in the game to find winning combinations of moves this week…

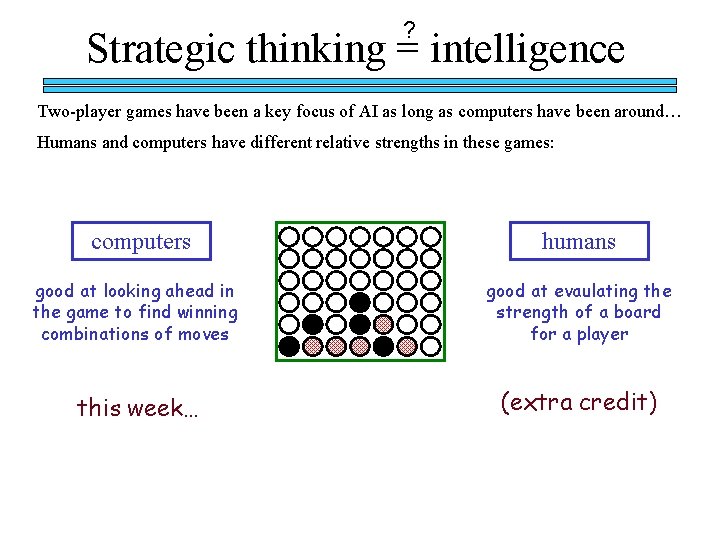
? Strategic thinking = intelligence Two-player games have been a key focus of AI as long as computers have been around… Humans and computers have different relative strengths in these games: computers humans good at looking ahead in the game to find winning combinations of moves good at evaulating the strength of a board for a player this week… (extra credit)

How humans play games… An experiment (by de. Groot) was performed in which chess positions were shown to novice and expert players… - experts could reconstruct these perfectly - novice players did far worse…

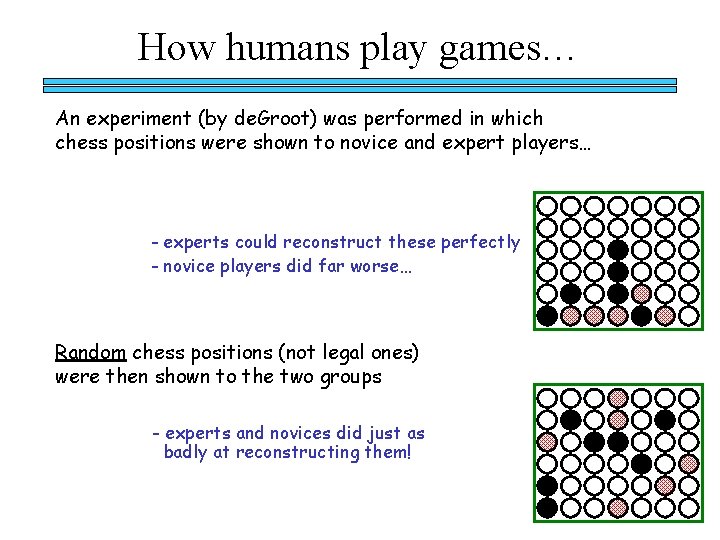
How humans play games… An experiment (by de. Groot) was performed in which chess positions were shown to novice and expert players… - experts could reconstruct these perfectly - novice players did far worse… Random chess positions (not legal ones) were then shown to the two groups - experts and novices did just as badly at reconstructing them!

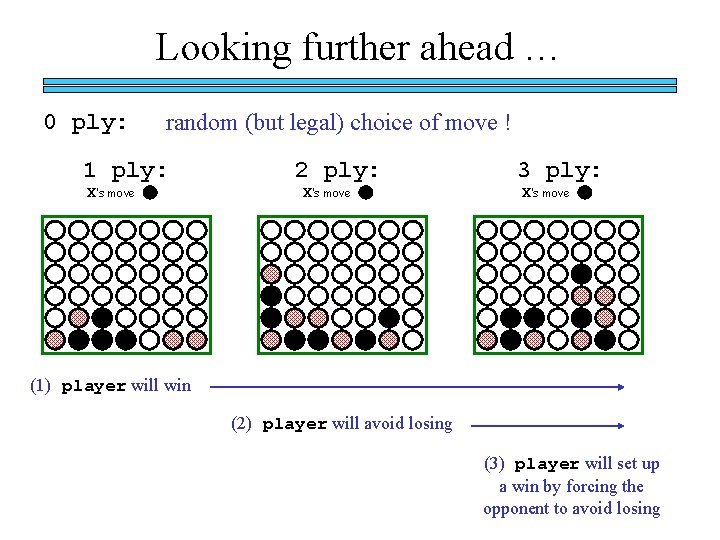
Looking further ahead … 0 ply: random (but legal) choice of move ! 1 ply: X’s move 2 ply: X’s move 3 ply: X’s move (1) player will win (2) player will avoid losing (3) player will set up a win by forcing the opponent to avoid losing

public double[] ply 2(Board b) { ply 2 depends on ply 1 !

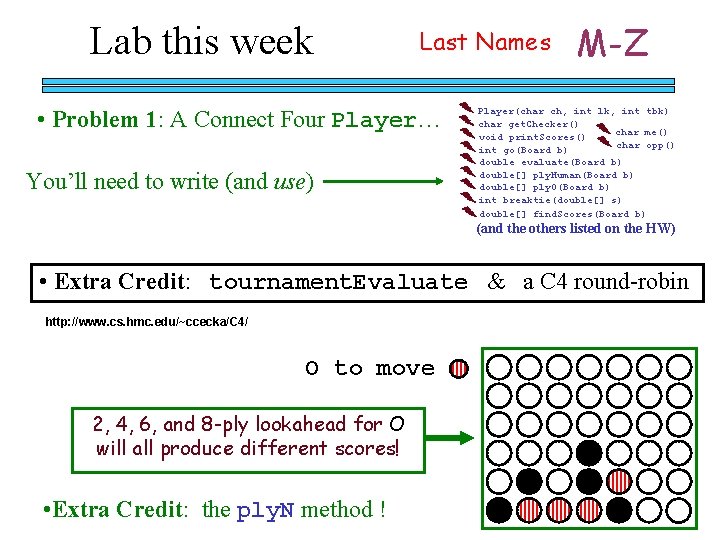
Lab this week Last Names • Problem 1: A Connect Four Player… You’ll need to write (and use) M-Z Player(char ch, int lk, int tbk) char get. Checker() char me() void print. Scores() char opp() int go(Board b) double evaluate(Board b) double[] ply. Human(Board b) double[] ply 0(Board b) int breaktie(double[] s) double[] find. Scores(Board b) (and the others listed on the HW) • Extra Credit: tournament. Evaluate & a C 4 round-robin http: //www. cs. hmc. edu/~ccecka/C 4/ O to move 2, 4, 6, and 8 -ply lookahead for O will all produce different scores! • Extra Credit: the ply. N method !

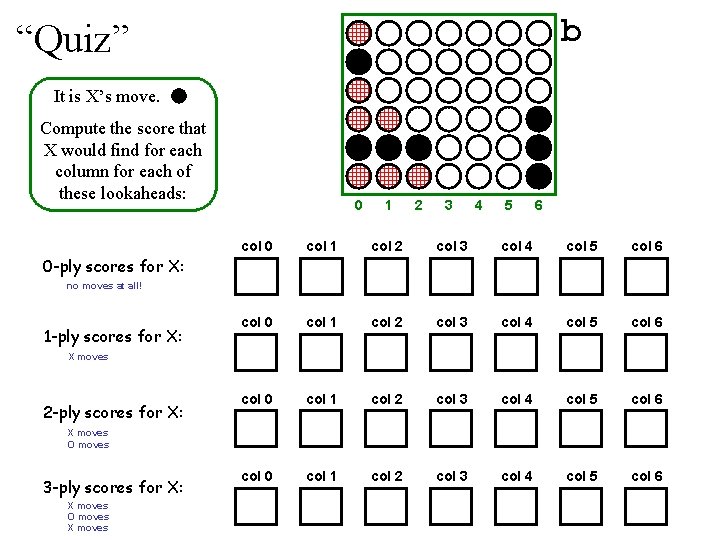
b “Quiz” It is X’s move. . Compute the score that X would find for each column for each of these lookaheads: 0 1 2 3 4 5 6 col 0 col 1 col 2 col 3 col 4 col 5 col 6 0 -ply scores for X: no moves at all! 1 -ply scores for X: X moves 2 -ply scores for X: X moves O moves 3 -ply scores for X: X moves O moves X moves

Write breaktie to return a randomly chosen best score (max score) from an array of scores named s. class Player { private int tiebreak. Type; private int lookahead; private char checker; public int breaktie(double[] s) { double max. Score = get. Max(s); /* assume get. Max is already written */ if (this. tiebreak. Type == 2) */ { } } } /* random tie breaker is tiebreak. Type == 2

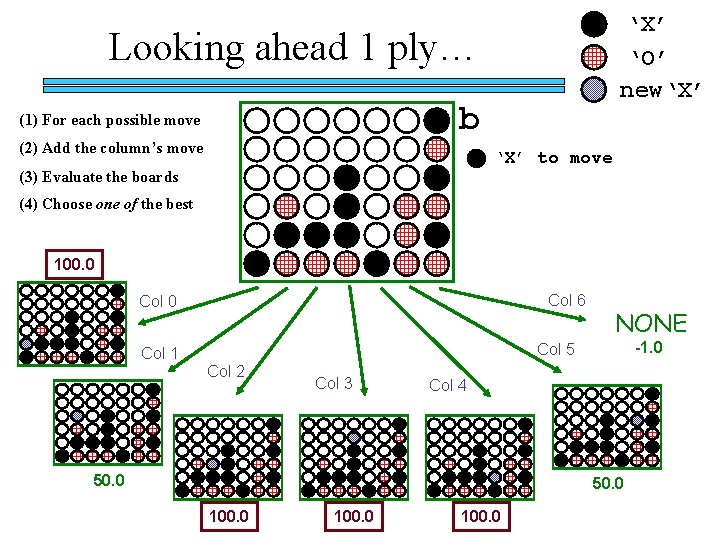
‘X’ ‘O’ new‘X’ Looking ahead 1 ply… b (1) For each possible move (2) Add the column’s move ‘X’ to move (3) Evaluate the boards (4) Choose one of the best 100. 0 Col 6 Col 0 NONE -1. 0 Col 5 Col 1 Col 2 Col 3 Col 4 50. 0 100. 0

Winning -- details complete HW 10 PR 2 solutions at http: //www. cs. hmc. edu/courses/2002/fall/cs 5/week_10/sols. html public boolean wins. For(char ox) { for (int r=0 ; r<this. n. Rows-3 ; ++r) { for (int c=0 ; c<this. n. Cols-3 ; ++c) { if (this. data[r+0][c+0] == ox && this. data[r+1][c+1] == ox && this. data[r+2][c+2] == ox && this. data[r+3][c+3] == ox) { return true; } } } … same idea for vert. , horiz. , SW-NE diag. … } return false; finds this diagonal: | | | | |X| | | | |O|X|O| | | |O|X|X| |O|O| |X|O|O|X|X|O|X| -------0 1 2 3 4 5 6.

static methods belong to a class, not an object H. pl(“I’m a static method”); // lots double av = average. Array(stocks); // HW 7 int syl = num. Syllables(word); // HW 6 double d = Math. sqrt(343. 0); If the static method is in another class, the class name is needed!

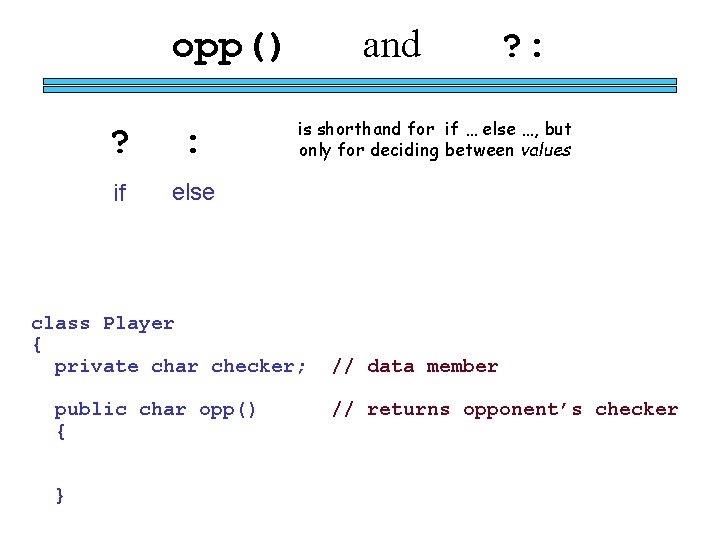
and opp() ? : if else is shorthand for if … else …, but only for deciding between values class Player { private char checker; public char opp() { } ? : // data member // returns opponent’s checker

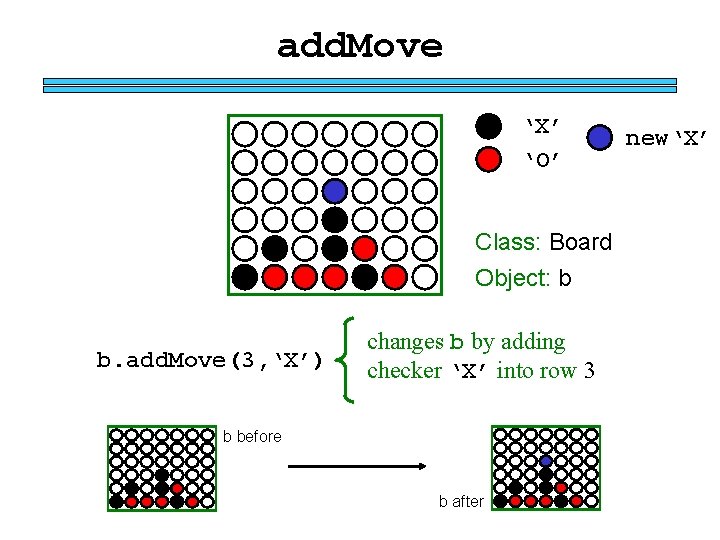
add. Move ‘X’ ‘O’ Class: Board Object: b b. add. Move(3, ‘X’) changes b by adding checker ‘X’ into row 3 b before b after new‘X’

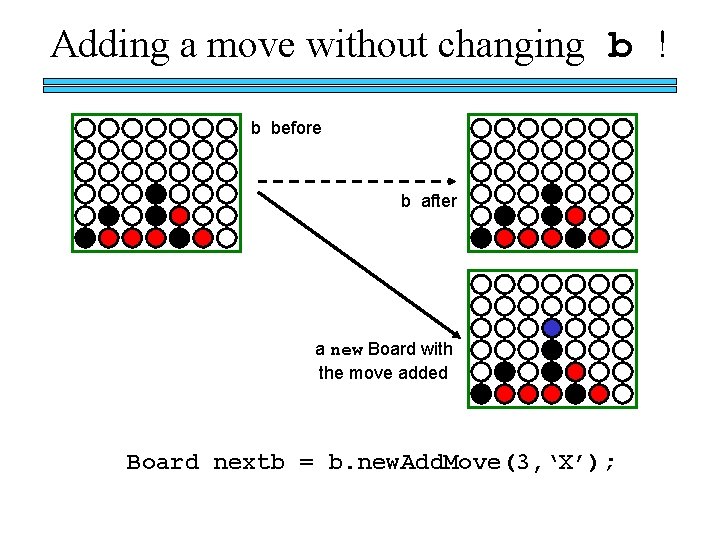
Adding a move without changing b ! b before b after a new Board with the move added Board nextb = b. new. Add. Move(3, ‘X’);