Todays Objective 1 1 To be able to

Today’s Objective (1) ► 1. ) To be able to line up the like terms of 2 polynomials. ► 2. ) To be able to add and subtract polynomials.

Terms to know ►Monomial - a number, variable, or product of either with only exponents of 0 or positive integers. y, -x, ab, (1/3)x, 2 2 3 xy , (abc ) 2 x, 8,

Special Note ►Monomial - No monomial has a variable as an exponent, nor does it have a variable in the denominator of a fraction. ► 3/y, a x

Terms to know ►Polynomial - is the sum or difference of monomials. ►Any Monomial is also a Examples polynomial 2 ►a-b, x, -2 x +xy-3, 2 ► 1/8 x - xy , r + 9, 6

Adding Polynomials ►Add 5 x + 7 and 8 - 2 x

Subtracting Polynomials subtract 3 a + b from 7 a + 5 b

Subtracting Polynomials ►Subtract 3 a + b from 7 a + 5 b

Adding Polynomials ►Add 2 c + 5 c + 4 and 3 c - 7 2 c + 5 c + 4 3 c - 7 2 c + 5 c + 3 c + 4 - 7 2 c + 8 c - 3

Adding Polynomials ►Add 2 c + 5 c + 4 and 3 c - 7 2 c + 5 c + 4 3 c - 7 2 c + 8 c - 3

Today’s Objective (2) ►To understand the similarities and differences of: ►Monomials (1) ►Binomials (2) ►Trinomials (3) ►Polynomials (Many)

Monomials ►Have ► 6, one term such as: 2 3 2 7 a, 5 x , -4 m n 3 2 -4 m n

►Have Binomials two terms such as 2 ► 5 x + 3, 6 y - 2, ►a - b, 2 2 x y - 2 3 xy The terms are separated by one operation sign (+ or -)

►Have ► ► Trinomials three terms such as: 2 3 x + 5 x - 6 -3 m + 3 m -2 The terms are separated by two operation signs (+ or -)

Be ready to answer the following questions: ► 1. ) What separates the terms of a polynomial? ► 2. ) How many signs separate the terms of a trinomial?

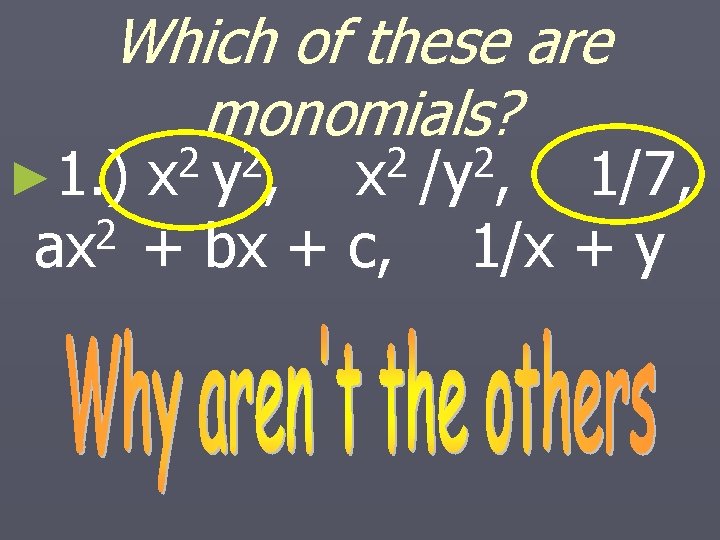
Which of these are monomials? ► 1. ) 2 ax 2 2 x y, 2 2 x /y , + bx + c, 1/7, 1/x + y

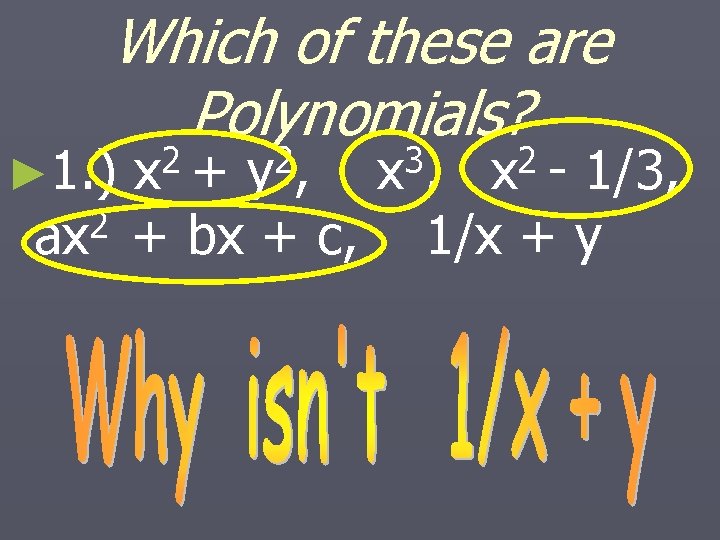
Which of these are Polynomials? ► 1. ) 2 ax 2 x + 2 y, + bx + c, 3 x, 2 x - 1/3, 1/x + y

Classifying Polynomials ►Polynomials are Classified by degree. ►The Degree is determined by the exponents of the terms.

The degree of a Monomial Degree ►Is the sum 3 x 3 of the 3 2 x y 5 exponents of 3 2 the variables 3 x y 5 of the 2 3 x y 5 monomial.

The degree of a Monomial Degree ►Is the sum of the 9 0 exponents of x 1 the variables x y 2 of the monomial.

The degree of a Polynomial ►Is the highest degree of any of its terms after the poly has been simplified. Polynomial 2 3 x + 5 x + 7 Degree 2

The degree of a Polynomial Degree 2 + 5 x + 7 2 3 x -9 xyz +y+z 3 1 x+y+7 2 2 2 x +7 x -3 y-2 x 2 2 3 x

Descending order of Polynomials ►From the highest degree to the lowest degree of the terms. 2 ► 3 x + 5 x + 7 3 2 ► 3 x + 5 x - 2 x +

Ascending order of Polynomials ►From the lowest degree to the highest degree of the terms. ► 7 2 3 x + 5 x + 2 3 ► 7 - 2 x + 5 x +3 x

Today’s Objective (3) Learn Basic Laws of Exponents Whenever we have variables which contain exponents and have equal bases, we can do certain mathematical operations to them. Those operations are called the “Laws of Exponents” x b is read ”b to the x power” b = base x = exponent

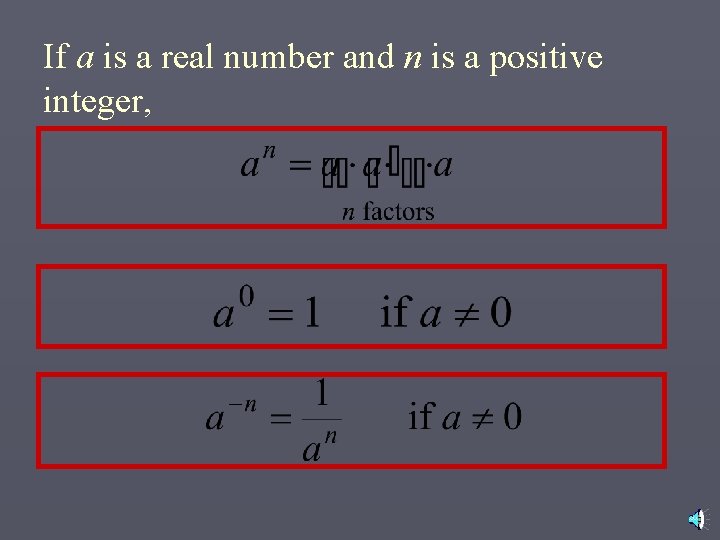
If a is a real number and n is a positive integer,

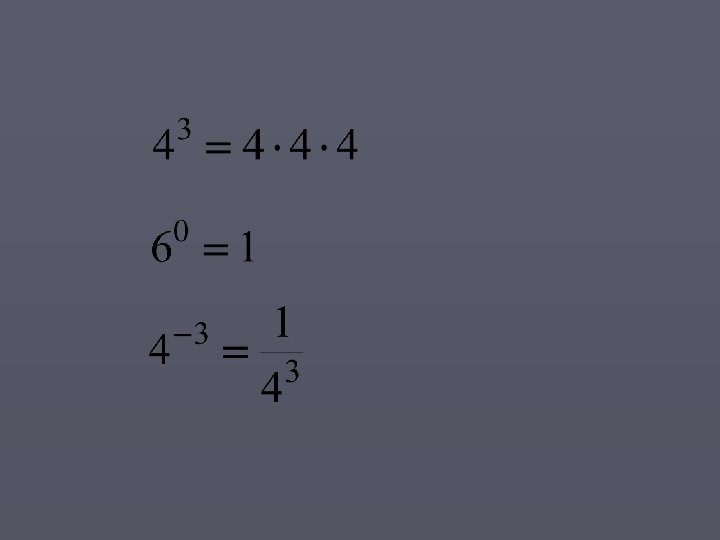
Basic Laws of Exponents

Other Properties of Exponents Any single number or variable is always to the first power

Basic Examples

More Examples