Thermalization and Quantum Information Fernando G S L

Thermalization and Quantum Information Fernando G. S. L. Brandão University College London partially based on joint work with Aram Harrow and Michal Horodecki New Perspectives on Thermalization, Aspen 2014

Plan Quantum Information Thermalization 1. Equivalence of microcanonical and canonical ensembles quantum information-theoretic proof 2. Equilibration by random unitary evolutions relation to unitary designs, quantum circuit complexity

Microcanonical and Canonical Ensembles Given a Hamiltonian of n particles : Microcanonical: Canonical:

Microcanonical and Canonical Ensembles When should we use each? Micro: System in isolation Macro: System in equilibrium with a heat bath at temperature 1/β What if we are only interested in expectation values of local observables? Is the system an environment for itself? i. e. For every e, is there a β(e) s. t. A X

Previous Results • Equivalence when A interacts weakly with Ac (Goldstein, Lebowitz, Tumulka, Zanghi ’ 06; Riera, Gogolin, Eisert ‘ 12) • Non-equivalence for critical systems (e. g. 2 D Ising model) (Desermo ’ 04) • Equivalence for infinite lattices in the “unique phase region” (i. e. only one KMS state). But no bounds on the size of A. (Lima ‘ 72; Muller, Adlam, Masanes, Wiebe ‘ 13)

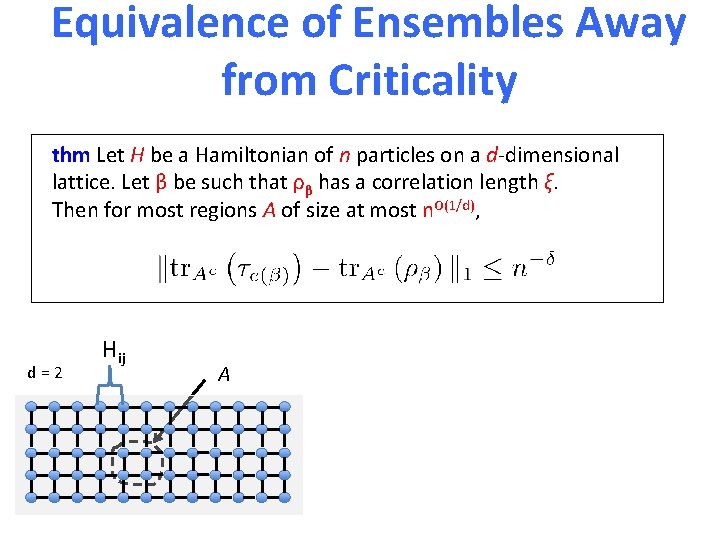
Equivalence of Ensembles Away from Criticality thm Let H be a Hamiltonian of n particles on a d-dimensional lattice. Let β be such that ρβ has a correlation length ξ. Then for most regions A of size at most n. O(1/d), d=2 Hij A

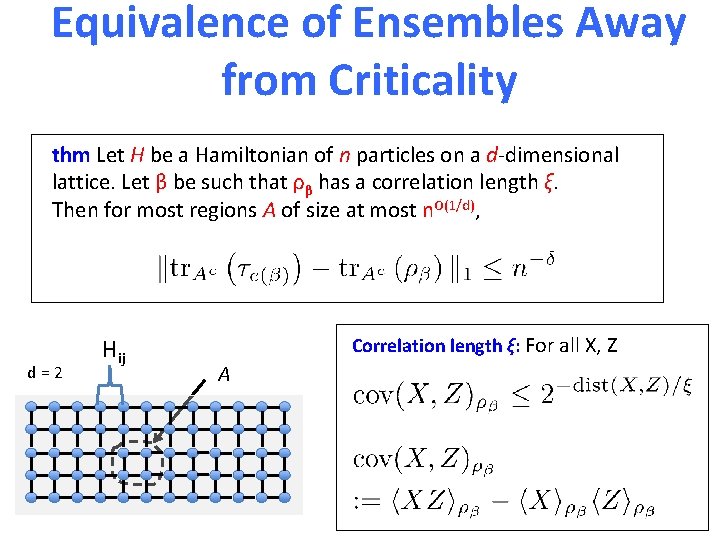
Equivalence of Ensembles Away from Criticality thm Let H be a Hamiltonian of n particles on a d-dimensional lattice. Let β be such that ρβ has a correlation length ξ. Then for most regions A of size at most n. O(1/d), d=2 Hij Correlation length ξ: For all X, Z A

Equivalence of Ensembles Away from Criticality thm Let H be a Hamiltonian of n particles on a d-dimensional lattice. Let β be such that ρβ has a correlation length ξ. Then for most regions A of size at most n. O(1/d), d=2 Hij Obs 1: e(β) given by mean energy of ρβ A Obs 2: Equivalent to for all observables X in A Obs 3: For every H, ρβ has finite ξ for β sufficiently small

Entropy and Relative Entropy: Subaditivity:

Entropy and Relative Entropy: Subaditivity: Relative Entropy: S(ρ || σ) measures the distinguishability of ρ and σ Positivity: Data Processing Inequality: Pinsker Ineq:

Free Energy and Relative Entropy Free energy: Easy-to-derive identity: For every state ρ, Relative Entropy: Obs: That ρβ minimizes free energy follows directly from positivity of relative entropy

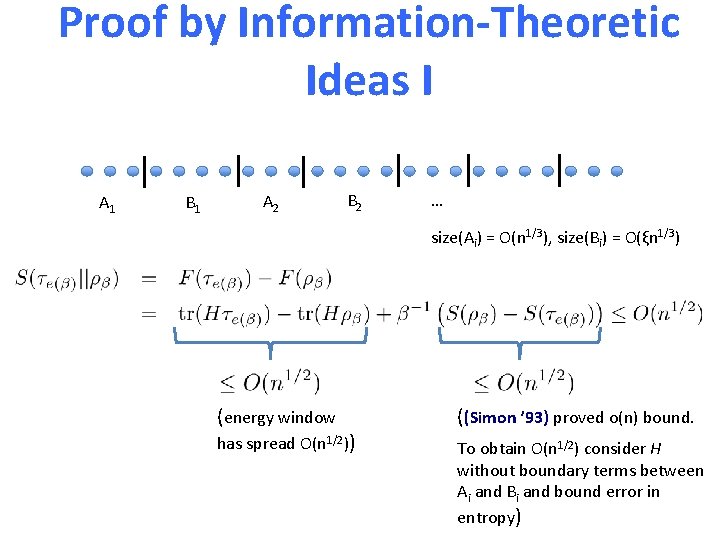
Proof by Information-Theoretic Ideas I A 1 B 1 A 2 B 2 … size(Ai) = O(n 1/3), size(Bi) = O(ξn 1/3)

Proof by Information-Theoretic Ideas I A 1 B 1 A 2 B 2 … size(Ai) = O(n 1/3), size(Bi) = O(ξn 1/3) (energy window has spread O(n 1/2)) ((Simon ’ 93) proved o(n) bound. To obtain O(n 1/2) consider H without boundary terms between Ai and Bi and bound error in entropy)

Proof by Information-Theoretic Ideas I What does A 1 B 1 A 2 imply? B 2 … size(Ai) = O(n 1/3), size(Bi) = O(ξn 1/3) (energy window has spread O(n 1/2)) ((Simon ’ 93) proved o(n) bound. To obtain O(n 1/2) consider H without boundary terms between Ai and Bi and bound error in entropy)

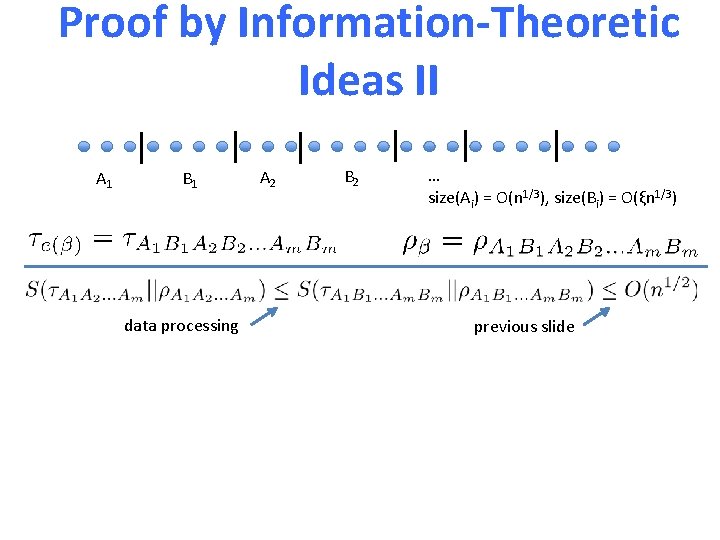
Proof by Information-Theoretic Ideas II A 1 B 1 data processing A 2 B 2 … size(Ai) = O(n 1/3), size(Bi) = O(ξn 1/3) previous slide

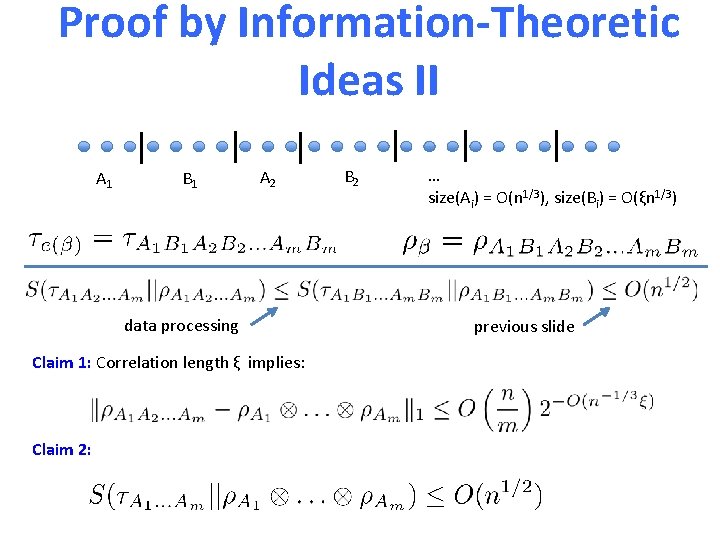
Proof by Information-Theoretic Ideas II A 1 B 1 A 2 data processing Claim 1: Correlation length ξ implies: Claim 2: B 2 … size(Ai) = O(n 1/3), size(Bi) = O(ξn 1/3) previous slide

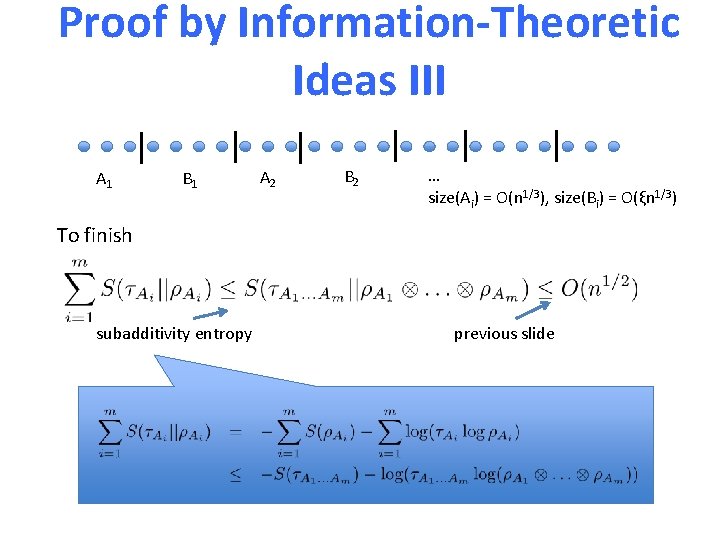
Proof by Information-Theoretic Ideas III A 1 B 1 A 2 B 2 … size(Ai) = O(n 1/3), size(Bi) = O(ξn 1/3) To finish subadditivity entropy previous slide

Proof by Information-Theoretic Ideas III A 1 B 1 A 2 B 2 … size(Ai) = O(n 1/3), size(Bi) = O(ξn 1/3) To finish subadditivity entropy Since m = O(n 2/3): By Pinsker inequality: previous slide

Further Implications (Popescu, Short, Winter ’ 05; Goldstein, Lebowitz, Timulka, Zanghi ‘ 06, …) Let H be a Hamiltonian and Se the subspace of states with energy (en, en + n 1/2). Then for almost every state |ψ> in Se, and region A sufficiently small, Consequence: If ρβ(e) has a correlation finite correlation length, Obs: Even stronger statement is conjectured to hold in some cases Eigenstate Thermalization Hypothesis: For most eigenstates |Ek> in Se

Plan Quantum Information Thermalization 1. Equivalence of microcanonical and canonical ensembles quantum information-theoretic proof 2. Equilibration by random unitary evolutions relation to unitary designs, quantum circuit complexity

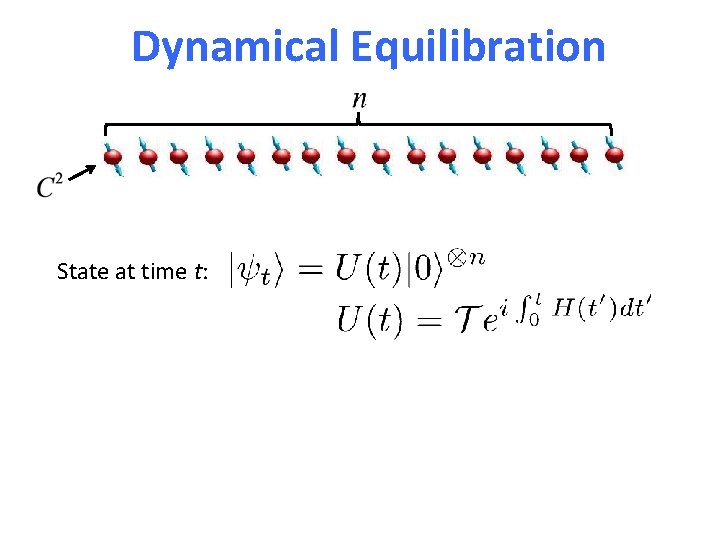
Dynamical Equilibration State at time t:

Dynamical Equilibration State at time t: Will equilibrate? I. e. for most t ?

Dynamical Equilibration State at time t: Will equilibrate? I. e. for most t ? NO!

Relative Equilibration How about relative to particular kind of measurements? Examples • “macroscopic” measurements (e. g. magnetization) • local measurements (e. g. measurements in the 3 first sites)

Equilibration is generic (Linden, Popescu, Short, Winter ’ 08) Almost* any Hamiltonian H equilibrates: with and *Almost: (Ei + Ej – Ek - El) all non-zero and |0 n> spread over energy eigenstates S E

Time Scale of Equilibration The previous general approach only gives exponentially long convergence bounds (in♯ of particles ) Goal: Show that Generic local dynamics leads to rapid equilibration Caveat: time-dependent Hamiltonians…

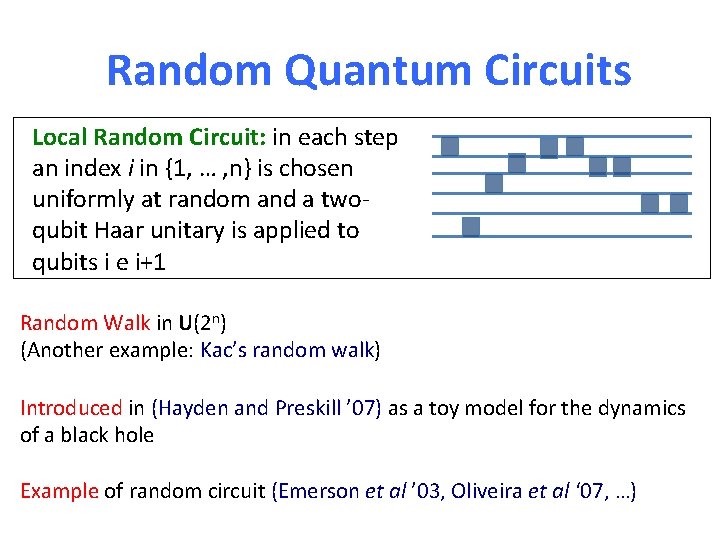
Random Quantum Circuits Local Random Circuit: in each step an index i in {1, … , n} is chosen uniformly at random and a twoqubit Haar unitary is applied to qubits i e i+1 Random Walk in U(2 n) (Another example: Kac’s random walk) Introduced in (Hayden and Preskill ’ 07) as a toy model for the dynamics of a black hole Example of random circuit (Emerson et al ’ 03, Oliveira et al ‘ 07, …)

Parallel Random Quantum Circuits Parallel Local Random Circuit: in each step n/2 independent Haar two -qubit gates are applied to either ((1, 2), (3, 4), …, (n-1, n)) or ((2, 3), (4, 5), …, (n-2, n-1)) Discrete version of with random H(t) = H 12(t) + H 23(t) + … + Hnn-1(t) (i. e. “brownian quantum circuits” (Lashkari, Stanford, Hastings, Osborne, Hayden ‘ 12))

How fast 1 D random circuits equilibrate? As fast as possible: (B. , Harrow, Horodecki ‘ 12) Let RCt be the set of all parallel circuits of depth t ≥ 100 n. For almost all U in RCt For every region S, |S| ≤ n/4: with S (Brown and Fawzi ‘ 13, ‘ 14) Generalization to any dim (t ≥ O(n 1/dpolylog(n)))

Warm-up: Equilibration for Haar Random Unitaries Haar measure (Page ‘ 93) Let and We have only second moments needed But So for S Sc Is there a similar argument for random circuits?

Warm-up: Equilibration for Haar Random Unitaries Haar measure (Page ‘ 93) Let and We have only second moments needed But So for S Sc Is there a similar argument for random circuits?

Unitary k-designs Def. An ensemble of unitaries {μ(d. U), U} in U(d) is an ε-approximate unitary k-design if for every monomial M = Up 1, q 1…Upk, qk. U*r 1, s 1…U*rk, sk, |Eμ(M(U)) – EHaar(M(U))|≤ ε • First k moments are close to the Haar measure • Natural quantum generalization of k-wise independent distributions • Many applications in quantum information

Random Quantum Circuits as k-designs? thm (B. , Harrow, Horodecki ‘ 12) Parallel Local Random Circuits of size O(k 5 n + k 4 log(1/ε)) are an ε-approximate unitary k-design • Previous results (Oliveira et al ‘ 07, Harrow&Low ‘ 08, Znidaric ‘ 08, Brown&Viola ‘ 09, …) Random circuits of size O(n(n + log(1/ε))) ε-approximate designs • Can replace Page’s calculation with k=2 and ε = 2 -O(n) to get • What does k > 2 gives?

Equilibration for low complexity measurements Given an observable M (POVM element 0 < M < id) in we define its circuit complexity as the minimum number of two-qubit gates needed to measure {M, id-M}. {0, 1} Let Mk : = { M : 0 ≤ M ≤ id, M has gate complexity k }. For almost all U in RCt with t ≥ O(k 6) and n ≤ k ≤ 2 O(n), • Shows U|0 n> is quantum pseudo random. • Circuit complexity of U is at least Ω(k).

Outline Proof Random Circuits are Polynomial Designs 1. Mapping the problem to bounding spectral gap of a Local Hamiltonian 2. Technique for bounding spectral gap (Nachtergaele ’ 94) + representation theory (reduces the problem to obtaining an exponentially small lower bound on the spectral gap) 3. Path Coupling applied to the unitary group (to prove convergence of the random walk in exponential time) 4. Use detectability Lemma (Arad et al ‘ 10) to go from local random circuits to parallel local random circuits

Conclusions • Quantum Information theory provides new tools for studying thermalization/equilibration and poses new questions about them Two examples: • Info-theoretical proof of equivalence of ensembles for noncritical systems. What are the conditions for critical systems (diverging correlation length)? • Equilibration of random quantum circuits. Can we prove equilibration for random time-independent Hamiltonians? Thanks!