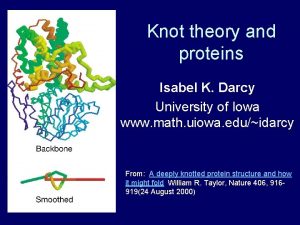
The Unknot the Trefoil Knot and the FigureEight


























- Slides: 38

The Unknot, the Trefoil Knot, and the Figure-Eight Knot are Mutually Nonequivalent An Elementary Proof Jimmy Gillan Thursday, April 10, 2008

Outline • Introduction – A Brief History of Knot Theory – What is a knot? – Knot Terminology • Defining Knots • Equivalence and Knot Invariants • The Proof

A Brief History of Knot Theory • Carl Friedrich Gauss (1777 – 1855) • Lord Kelvin, atoms, and the “ether” • P. G. Tait first to formally publish a paper on knots in 1877 – Enumerating and tabulating knots • Early 20 th century classical knot theory becomes a formal branch of mathematics • Knot theory now includes elements of algebra, combinatorics and geometry

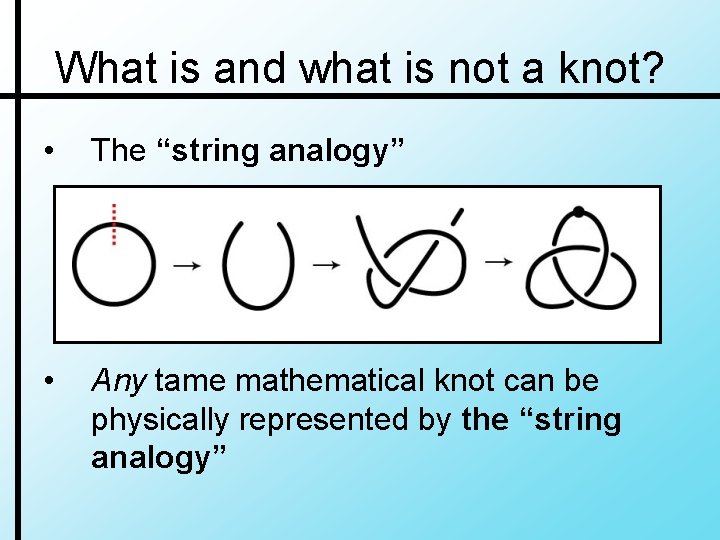
What is and what is not a knot? • The “string analogy” • Any tame mathematical knot can be physically represented by the “string analogy”

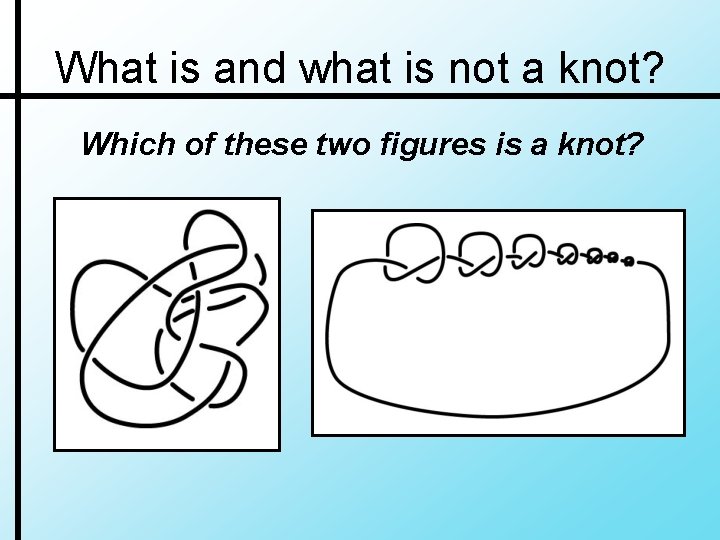
What is and what is not a knot? Which of these two figures is a knot?

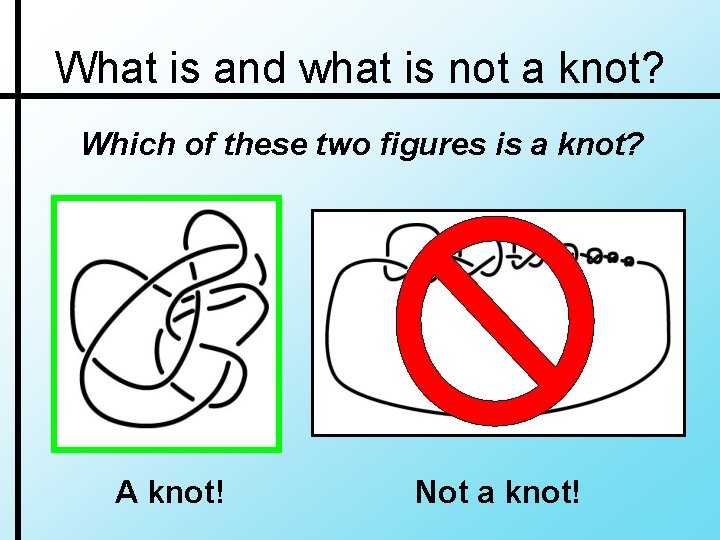
What is and what is not a knot? Which of these two figures is a knot? A knot! Not a knot!

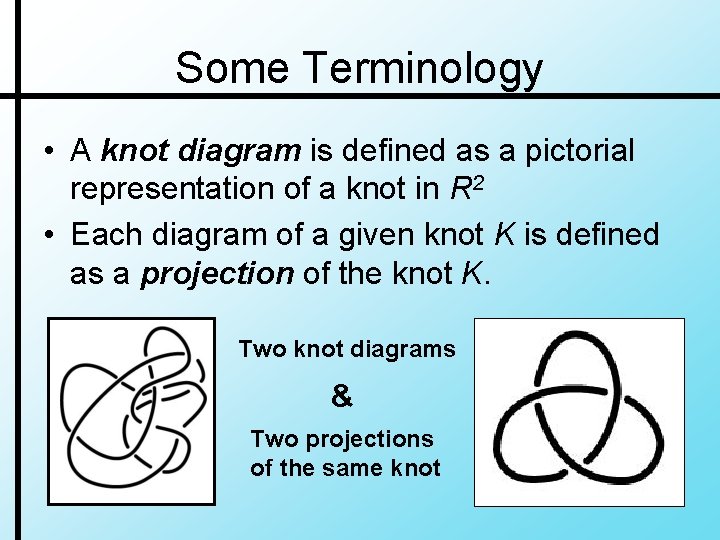
Some Terminology • A knot diagram is defined as a pictorial representation of a knot in R 2 • Each diagram of a given knot K is defined as a projection of the knot K. Two knot diagrams & Two projections of the same knot

Some Terminology • A crossing is defined as a point in the projection of a knot where the knot intersects or crosses-over itself.

Defining Knots Topological Definition • A knot is an embedding of S 1 in R 3 or S 3. Simpler Definition • A knot is a defined as a simple, closed curve in R 3 that is isotopic to a simple, closed polygonal curve with a finite vertex set.

Defining Knots • • • Let K be a curve in R 3 and let f: I → R 3 be a continuous function such that f (I) = K. closed – f (0) = f (1) simple – if f (x) = f (y), then either x = y or x, y ε {0, 1}

Defining Knots • • • A simple, closed polygonal curve is defined as follows: Let (p 1, …, pn) be an ordered set of points in R 3 such that no three points lie on a common line Let [pi, pj] denote the line segment between points pi and pj

Defining Knots • Two curves are said to be isotopic if one can be deformed to form the other in R 3 without breaking the curve at any point The simple, closed polygonal curve determined by (a, b, c) and a knot to which it is isotopic.

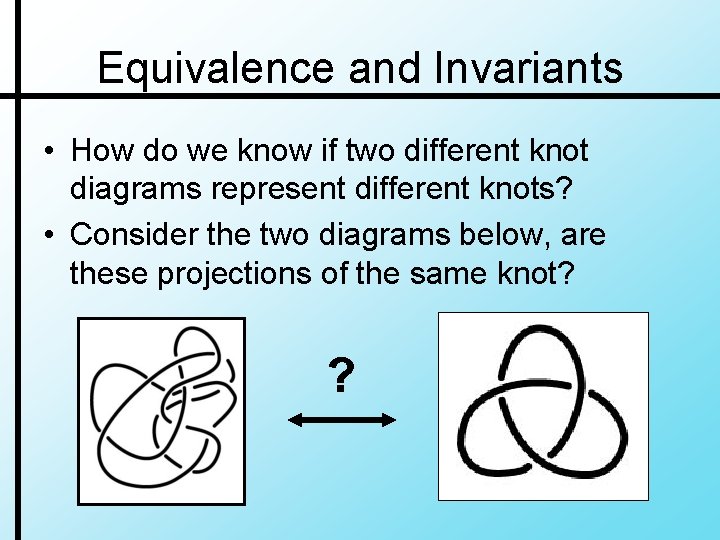
Equivalence and Invariants • How do we know if two different knot diagrams represent different knots? • Consider the two diagrams below, are these projections of the same knot? ?

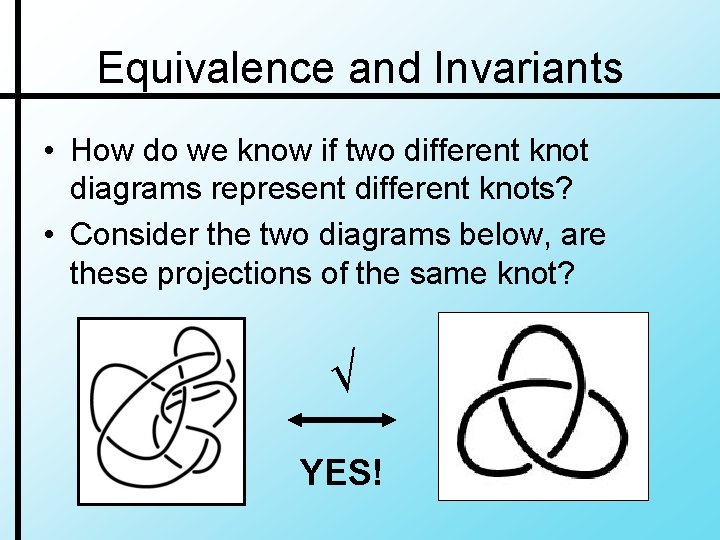
Equivalence and Invariants • How do we know if two different knot diagrams represent different knots? • Consider the two diagrams below, are these projections of the same knot? √ YES!

Equivalence and Invariants • Two projections are equivalent if you can deform one into the other without breaking the knot (“string analogy”) • Planar isotopies –deformations that do not change the crossings of a projection

Equivalence and Invariants • Reidemeister moves TYPE I OR TYPE III OR

Equivalence and Invariants Alexander and Briggs Theorem If two knot projections are equivalent, then their diagrams are related by a series of Reidemeister moves • A knot invariant is defined as a characteristic of a knot which is true for all of its projections • Use knot invariants to determine whether two knots are not equivalent

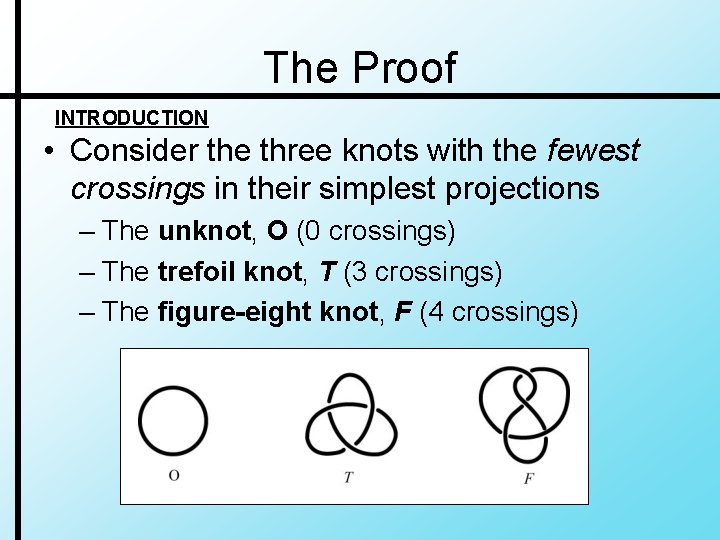
The Proof INTRODUCTION • Consider the three knots with the fewest crossings in their simplest projections – The unknot, O (0 crossings) – The trefoil knot, T (3 crossings) – The figure-eight knot, F (4 crossings)

The Proof OUTLINE O, T and F are mutually nonequivalent Sketch of Proof • First show T is not equivalent to O or F using the knot invariant Tricolorability • Then show O and F are not equivalent using the knot invariant the Jones Polynomial

The Proof TRICOLORABILITY • A knot is tricolorable if the pieces of a projection that are not intersected in its diagram can be colored with exactly 3 different colors such that at each crossing in the knot is the meeting of either 3 different colors or the same color. Is the trefoil knot T tricolorable?

The Proof TRICOLORABILITY • A knot is tricolorable if the pieces of a projection that are not intersected in its diagram can be colored with exactly 3 different colors such that at each crossing in the knot is the meeting of either 3 different colors or the same color. Is the trefoil knot T tricolorable? YES!

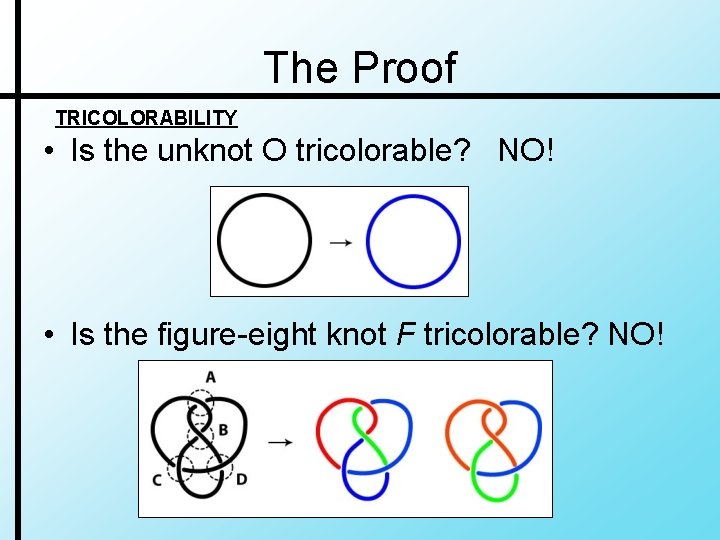
The Proof TRICOLORABILITY • Is the unknot O tricolorable? NO! • Is the figure-eight knot F tricolorable? NO!

The Proof THE JONES POLYNOMIAL • Assign a Laurent polynomial to each knot • If two projections have different polynomials, they are not equivalent • J. W. Alexander [1928] - developed first knot polynomial using matrices & determinants • John Conway [1969] - calculate the Alexander polynomial using skein relations • Vaughn Jones [1984] developed a way to calculate the Alexander polynomial using the bracket polynomial and skein relations

The Proof THE JONES POLYNOMIAL • The Jones polynomial of a knot K is defined as: where: – – X(K) is the Jones polynomial of K < K > denotes the bracket polynomial of K w(K) denotes the writhe of K A is the variable of bracket polynomial and A = t -1/4

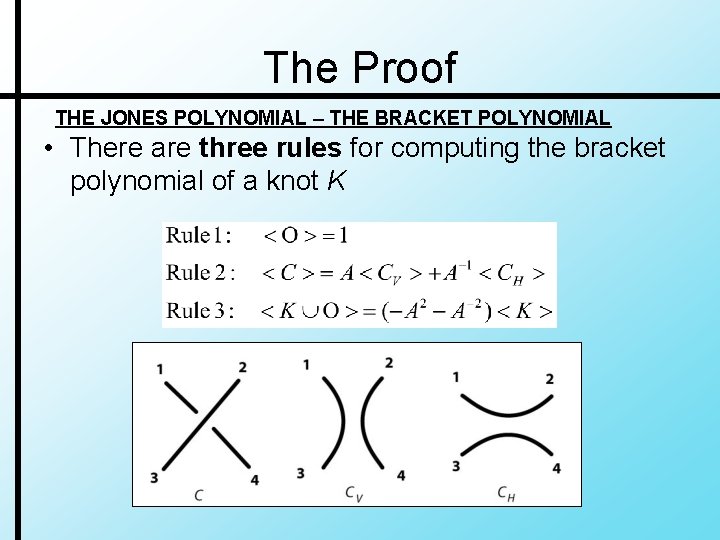
The Proof THE JONES POLYNOMIAL – THE BRACKET POLYNOMIAL • There are three rules for computing the bracket polynomial of a knot K

The Proof THE JONES POLYNOMIAL – BRACKET POLYNOMIAL • By Rule 1, <O> = 1 • Computing the bracket polynomial of F is more involved Take the projection of F and enumerate the crossings

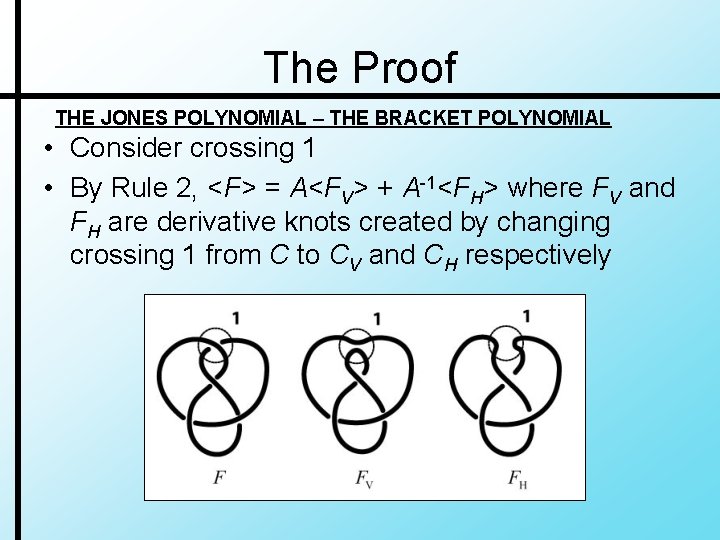
The Proof THE JONES POLYNOMIAL – THE BRACKET POLYNOMIAL • Consider crossing 1 • By Rule 2, <F> = A<FV> + A-1<FH> where FV and FH are derivative knots created by changing crossing 1 from C to CV and CH respectively

The Proof THE JONES POLYNOMIAL – THE BRACKET POLYNOMIAL • We must use Rule 2 again with crossing 2 in order to compute both <FV> and <FH>, giving us four derivative knots, <FVV>, <FVH>, <FHV>, and <FHH> with: • By substituting into the formula for <F> we get:

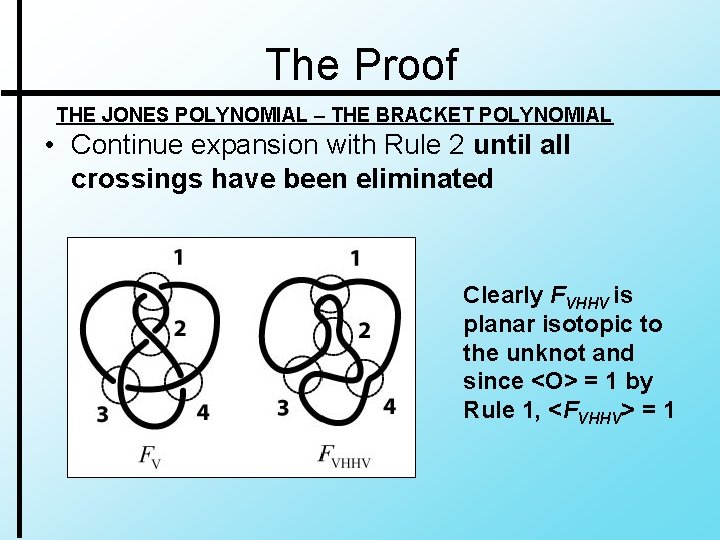
The Proof THE JONES POLYNOMIAL – THE BRACKET POLYNOMIAL • Continue expansion with Rule 2 until all crossings have been eliminated Clearly FVHHV is planar isotopic to the unknot and since <O> = 1 by Rule 1, <FVHHV> = 1

The Proof THE JONES POLYNOMIAL – THE BRACKET POLYNOMIAL • Now Rules 1 and 3 can be used to compute the values of the resulting 16 derivative knots and have <F> in terms of A • After lots of drawing and simplification we ultimately get:

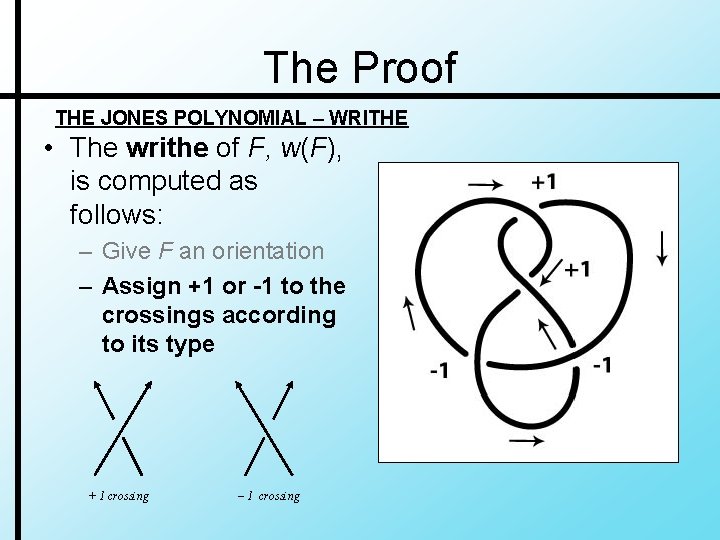
The Proof THE JONES POLYNOMIAL – WRITHE • The writhe of F, w(F), is computed as follows:

The Proof THE JONES POLYNOMIAL – WRITHE • The writhe of F, w(F), is computed as follows: – Give F an orientation

The Proof THE JONES POLYNOMIAL – WRITHE • The writhe of F, w(F), is computed as follows: – Give F an orientation – Assign +1 or -1 to the crossings according to its type + 1 crossing – 1 crossing

The Proof THE JONES POLYNOMIAL – WRITHE • The writhe of F, w(F), is computed as follows: – Give F an orientation – Assign +1 or -1 to the crossings according to its type – Sum the assignments over all crossings

The Proof THE JONES POLYNOMIAL – COMBINING THE TWO • Substitute the bracket polynomial and writhe of F and O into the original equation and replace A with t -1/4 • Clearly X(F) ≠ X(O)

The Proof CONCLUSION • T is not equivalent to O and T is not equivalent to F because T is tricolorable and O and F are not • O and F are not equivalent because their Jones polynomials are different • Thus O, T and F are mutually nonequivalent □

Thank You I’d like to thank my advisors, Professor Ramin Naimi and Professor Ron Buckmire, and the Occidental Mathematics Department for all their help and support over the last four years. Thank you for coming!

References • Adams, Colin C. , The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots, (New York, NY: W. H. Freeman and Company, 1994) • Kauffman, Louis H. , On Knots, (Princeton, NJ: Princeton University Press, 1987) • Livingston, Charles, Knot Theory, (Washington, D. C. : Mathematical Association of America, 1993)
 Thief knot vs square knot
Thief knot vs square knot Venture abroad trefoil guild
Venture abroad trefoil guild شرح قصيدة come sleep بالعربي
شرح قصيدة come sleep بالعربي Macam macam ikatan dan kegunaannya
Macam macam ikatan dan kegunaannya Arrow of light knot
Arrow of light knot 30 pieces of silver allusion
30 pieces of silver allusion Chinese knot tutorial
Chinese knot tutorial Mythical allusion definition
Mythical allusion definition Double figure 8 knot
Double figure 8 knot Tiedid
Tiedid Square knot for restraints
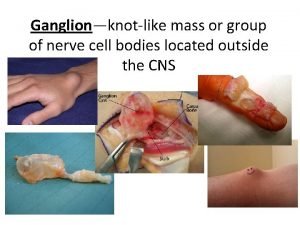
Square knot for restraints Knot like mass of nerve cell bodies
Knot like mass of nerve cell bodies Loaves and fishes allusion
Loaves and fishes allusion Cmsa wood
Cmsa wood Half boson knot
Half boson knot Rüzgar yönleri isimleri
Rüzgar yönleri isimleri Mummy restraint meaning
Mummy restraint meaning Viennese knot
Viennese knot What is a knot
What is a knot How long do dog periods last
How long do dog periods last Dog periods
Dog periods Knot tying ppt
Knot tying ppt Bell ringers knot
Bell ringers knot Clove hitch
Clove hitch Enamel parts
Enamel parts 4 tailed bandage
4 tailed bandage Hình ảnh bộ gõ cơ thể búng tay
Hình ảnh bộ gõ cơ thể búng tay Ng-html
Ng-html Bổ thể
Bổ thể Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Chó sói
Chó sói Tư thế worm breton là gì
Tư thế worm breton là gì Alleluia hat len nguoi oi
Alleluia hat len nguoi oi Môn thể thao bắt đầu bằng từ đua
Môn thể thao bắt đầu bằng từ đua Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Công thức tính thế năng
Công thức tính thế năng Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Cách giải mật thư tọa độ
Cách giải mật thư tọa độ