The transition rate W the Golden Rule of
























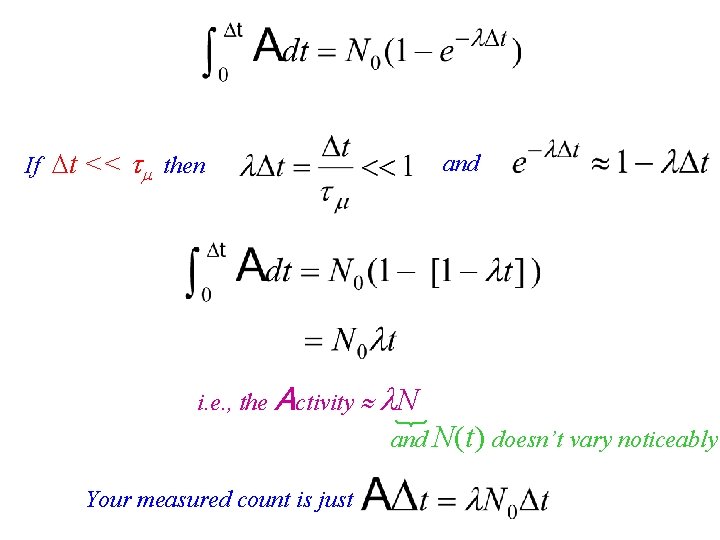
- Slides: 29

The transition rate, W (the “Golden Rule”) of initial final is also invoked to understand a b+c (+ ) decays Some observed decays n p + e- + e - e - + e + 20 10 * Ne 13 7 Fundamental particle decays 20 Ne + 10 N 13 6 C + e + + e Nuclear decays Pu 232 92 U + 236 94 How do you calculate an “overlap” between ? ? ?




It almost seems a self-evident statement: Any decay that’s possible will happen! What makes it possible? What sort of conditions must be satisfied? Total charge q conserved. J conserved.

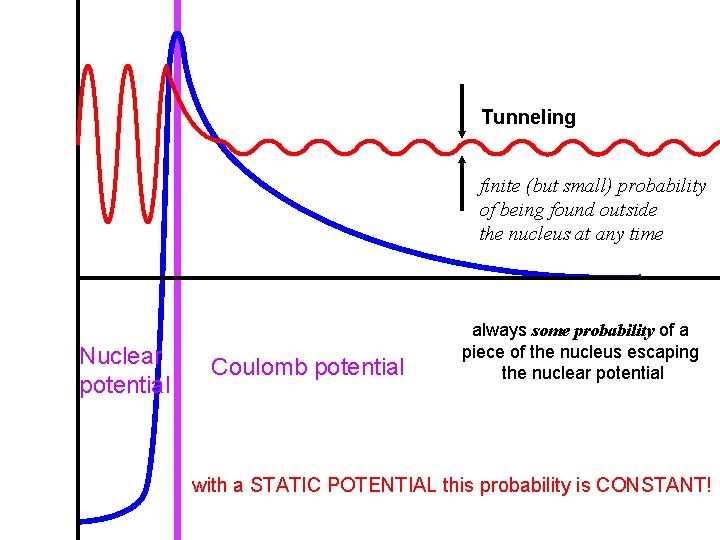
Tunneling finite (but small) probability of being found outside the nucleus at any time Nuclear potential Coulomb potential always some probability of a piece of the nucleus escaping the nuclear potential with a STATIC POTENTIAL this probability is CONSTANT!

probability of decaying (at any time - now or later) = constant ? ? What’s this mean equally likely at any instant ? ? must be expressed as a probability per unit time If we observe one, isolated nucleus it is equally likely it decays this moment t as any other moment t (even years from now) It either decays or it doesn’t.

Suppose a given particle has a 0. 01 probability of decaying in any given sec. Does this mean if we wait 100 sec it will definitely have decayed? If we observe a large sample N of such particles, within 1 sec how many can we expect to have decayed? Even a tiny speck of material can include well over trillions and trillions of atoms!

# decays N (counted by a geiger counter) the size of the sample studied t time interval of the measurement each decay represents a loss in the original number of radioactive particles fraction of particles lost Note: for 1 particle this must be interpreted as the probability of decaying. This argues that: -constant this is what the means!

If events occur randomly in time, (like the decay of a nucleus) the probability that the next event occurs during the very next second is as likely as it not occurring until 10 seconds from now. T) True. F) False.

P(1) Probability of the first count occurring in in 1 st second P(10) Probability of the first count occurring in in 10 th second i. e. , it won’t happen until the 10 th second ? ? ? P(1) = ? ? ? P(10) P(1000) P(10000)

Imagine flipping a coin until you get a head. Is the probability of needing to flip just once the same as the probability of needing to flip 10 times? Probability of a head on your 1 st try, P(1) = 1/2 Probability of 1 st head on your 2 nd try, P(2) = 1/4 Probability of 1 st head on your 3 rd try, P(3) = 1/8 Probability of 1 st head on your 10 th try, P(10) = (1/2)10 = 1/1024

What is the total probability of ALL OCCURRENCES? P(1) + P(2) + P(3) + P(4) + P(5) + • • • =1/2+ 1/4 + 1/8 + 1/16 + 1/32 + • • •

A six-sided die is rolled repeatedly until it gives a 6. What is the probability that one roll is enough? 1/6 What is the probability that it will take exactly 2 rolls? (probability of miss, 1 st try) (probability of hit)= What is the probability that exactly 3 rolls will be needed?

imagine the probability of decaying within any single second is p = 0. 10 the probability of surviving that same single second is p = 0. 90 P(N) probability that it decays in the Nth second (but not the preceeding N-1 seconds) P(1) P(2) P(3) P(4) P(5) P(6) P(7) P(8) P(9) = 0. 10 = = 0. 902 0. 10 = = 0. 903 0. 10 = = 0. 904 0. 10 = = 0. 905 0. 10 = = 0. 906 0. 10 = = 0. 907 0. 10 = = 0. 908 0. 10 =


Probability of living to time t=N sec, but decaying in the next second (1 -p)Np Probability of decaying instantly (t=0) is? 0 Probability of living forever (t ) is? 0

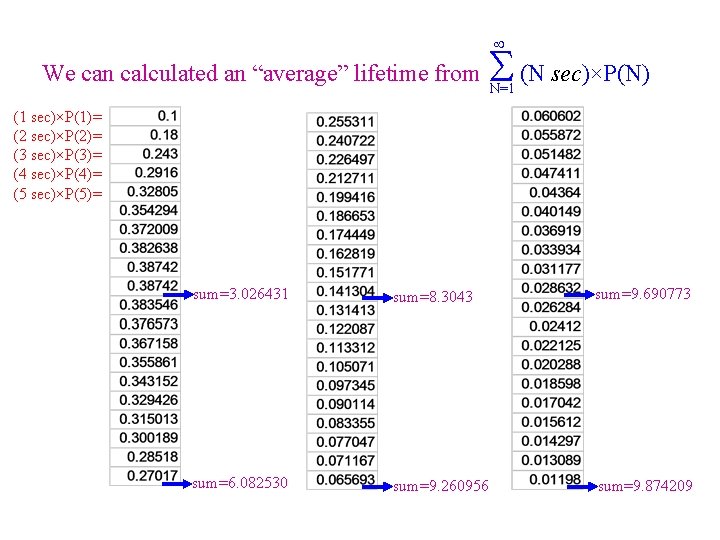
We can calculated an “average” lifetime from S (N sec)×P(N) N=1 (1 sec)×P(1)= (2 sec)×P(2)= (3 sec)×P(3)= (4 sec)×P(4)= (5 sec)×P(5)= sum=3. 026431 sum=8. 3043 sum=9. 690773 sum=6. 082530 sum=9. 260956 sum=9. 874209

the probability of decaying within any single second p = 0. 10 = 1/ where of course is the average lifetime (which in this example was 10, remember? )

The probability that the particle has decayed after waiting N seconds must be cumulative, i. e. Probability has decayed after 2 seconds: P(1)+P(2) after 3 seconds: P(1)+P(2)+P(3) after 4 seconds: P(1)+P(2)+P(3)+P(4) P(1)= P(1)+P(2)+P(3)= P(1)+P(2)+P(3)+P(4)=


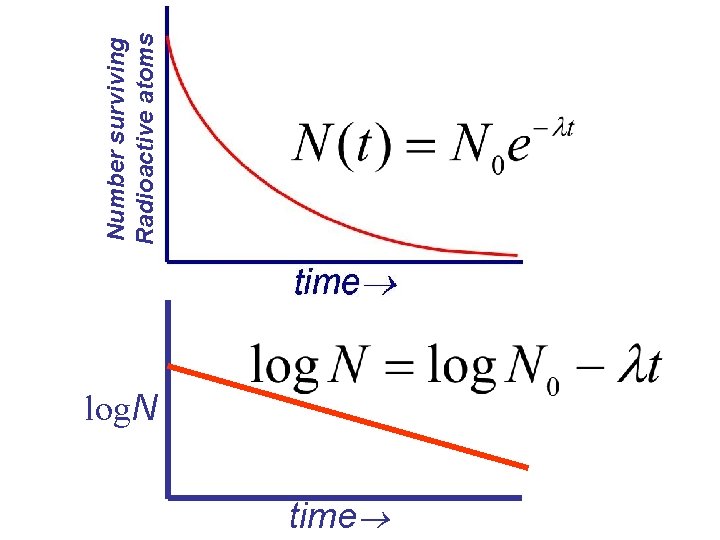
This exponential behavior can be summarized by the rules for our imagined sample of particles fraction surviving until time t fraction decaying by time where = 1/ t = e- t = (1 - e- t ) (and is the average lifetime)

or probability of surviving through to time t then decaying that moment (within t and t)

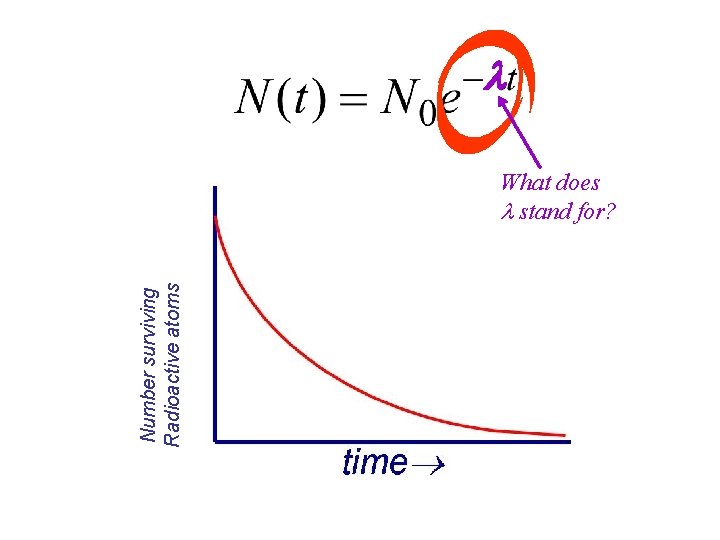
Number surviving Radioactive atoms What does stand for?

log. N time Number surviving Radioactive atoms

probability of still surviving by the time t # decaying within dt Notice: this varies with time! This is the number that survive until t but then decay within the interval t and t + dt Thus the probability of surviving until t but decaying within t and t + dt

the probability of surviving until t but decaying within t and t + dt If then gives the average “lifetime” 0 -0 = 1/

What is directly measured is a “disintegration rate” or ACTIVITY but only over some interval t of observation:
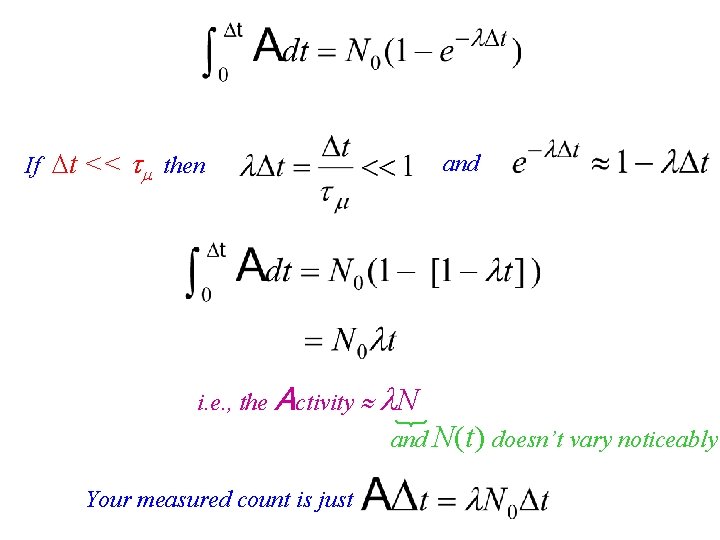
If t << then and i. e. , the Activity N and N(t) doesn’t vary noticeably Your measured count is just
 Golden ratio in the last supper
Golden ratio in the last supper Modified fibonacci sequence
Modified fibonacci sequence United healthcare underwritten by golden rule
United healthcare underwritten by golden rule Advantages and disadvantages of the mischief rule
Advantages and disadvantages of the mischief rule Shelf prospectus
Shelf prospectus Golden rule of framing the prospectus
Golden rule of framing the prospectus The golden rule in all religions
The golden rule in all religions Rule.io
Rule.io Fermi golden rule
Fermi golden rule Fermi golden rule
Fermi golden rule R v harris (1836) 7 c & p 446
R v harris (1836) 7 c & p 446 What is the golden rule in insurance ethics
What is the golden rule in insurance ethics Whitely v chappel (1868)
Whitely v chappel (1868) Golden rule of listening
Golden rule of listening Noc golden rule
Noc golden rule Magor and st mellons v newport corporation
Magor and st mellons v newport corporation Mischief rule
Mischief rule A meaningful authentic good life is based on
A meaningful authentic good life is based on Stair climbing golden rule is
Stair climbing golden rule is Cieh level 2 food hygiene
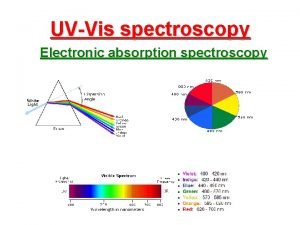
Cieh level 2 food hygiene Spectroscopy principle
Spectroscopy principle Microstate table for d3
Microstate table for d3 Transition rule
Transition rule Selection rule for electronic transition
Selection rule for electronic transition Selection rule for electronic transition
Selection rule for electronic transition Cap rate interest rate relationship
Cap rate interest rate relationship Nominal v. real interest rates
Nominal v. real interest rates Growth analysis definition
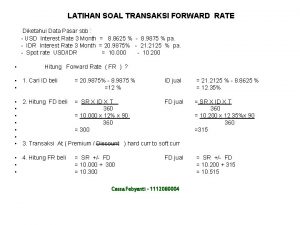
Growth analysis definition Contoh transaksi forward
Contoh transaksi forward Determination of exchange rate
Determination of exchange rate