18 Photons and Atoms The Tools We Will

18. Photons and Atoms The Tools We Will Use • Want to let photons interact with “atoms” • We will use time-dependent perturbation theory with constant perturbations • For final states different from initial, rates determined from Fermi’s Golden Rule: • The transition matrix is • The matrix elements are

18 A. The Hamiltonian Writing the Hamiltonian in Coulomb Gauge • Consider an atom with N electrons, and a quantized electromagnetic field: • The potential V contains all the terms concerning the electrons interacting with nuclei and with each other – Probably including things like spin-orbit coupling • The V term includes the electrostatic potential U(Rj) – Recall, in Coulomb gauge, this is determined by charge density • Note that A, B, and Rj are all operators • They include any interaction with external EM fields, but not electrons interacting with each other

Breaking out the Perturbation • Break Hamiltonian into four parts: • These parts are: • The unperturbed Hamiltonian will be: • It makes sense to break up W this way since W(2) is second order in the small coupling e, while W(1) is first order in e • When we do perturbation theory, we will count the “order” of perturbation theory by the number of factors of e

Eigenstates of the Unperturbed Hamiltonian • We will assume that the eigenstates of the atom are known: • We already know the eigenstates and energies of Hem • The eigentates and energies of H 0 are therefore

Writing Out the Perturbations • Note there is no time-dependence • Recall that A and B are given by: • Note that • We therefore have: • And also:

Comments on Perturbations • Note that W(1) can – Create one photon – Annihilate one photon • In contrast, W(2) can – Create two photons – Annihilate two photons – Create and annihilated one each • Generally not in the same momentum or polarization state

18 B. Emission and Absorption of Photons Which Terms Contribute? • We will consider leading order effect where we only emit or absorb one photon • Rename n 1, k 1, 1 and 1 as n, k, and because these interest us the most • Energy of initial and final states: • Fermi’s Golden Rule conserves energy: • Therefore – Energy goes up for absorption, down for emission • Leading order contribution is – First order in e • W(2) cannot create/annihilate a single photon • Higher order contributions are at least third order in e

Absorption of Photons • Let’s first consider absorption only, so there are n – 1 photons in final state • Only the annihilation term contributes • In the sum on k and , only the term with the correct state contributes • The photon part factors out: • So we have:

Dipole Approximation • As we did back in chapter 15, one can argue that k Rj and Sj k are small • Then we use a trick we found there: • So we have: • Substitute in Fermi’s Golden Rule: • Rewrite with fine structure constant • And use

Discussion • Compare with the formula we found before: • Intensity is energy density times velocity – This formula is identical to what we found before • We used the electric dipole approximation here • We could have used magnetic dipole, electric quadrupole, same as before • For photon absorption, the formulas are always identical

Emission of Photons • Now let’s consider emission only, so there are n + 1 photons in final state: • The photon parts factors out: • So we have: • Dipole approximation: • Proceed to final answer as before:

Spontaneous Emission • The term proportional to n is exactly what we got before • The new term is called spontaneous emission • Note it is zero in the limit V – You are trying to get it into a particular final state momentum k • Instead, sum over momentum states k • In the infinite volume limit, sum on k becomes an integral:

Summing Over Polarizations and Angles • Do the k integral, using = ck but for now, leave the others undone • • • To simplify, assume r. FI is real Let be angle between k and r. FI: One polarization yields zero dot product The other gives a sin factor: If we sum on polarizations and angles, we have:

Sample Problem An electron is trapped in the spherical infinite square well of radius a in the state |2, 1, 0. Calculate the rate for spontaneous emission to fall to the ground state |1, 0, 0. The relevant wave functions and energies are listed below. • We need to find:

Sample Problem An electron is trapped in the spherical infinite square well of radius a in the state |2, 1, 0. Calculate the rate for spontaneous emission to fall to the ground state |1, 0, 0. The relevant wave functions and energies are listed below. • Now substitute in:

Beyond the Dipole Approximation • As before, sometimes the dipole term doesn’t contribute • We can look to higher order terms to give additional contributions • First term is electric dipole: • Second is electric quadrupole: • Third is magnetic dipole:

Sample Problem An electron is trapped in a cubical infinite square well of side a in the state |2, 2, 1. Calculate the rate for spontaneous emission to fall to the ground state |1, 1, 1. • Initial and final wave functions and energies: • These functions are orthogonal: • To get a non-zero expression, we cannot use dipole: • In contrast, quadrupole will not be zero • Can show magnetic dipole does not contribute

Sample Problem (2) An electron is trapped in a cubical infinite square well of side a in the state |2, 2, 1. Calculate the rate for spontaneous emission to fall to the ground state |1, 1, 1. • All other components vanish • We need to find: • The matrix element is: • The frequencies are: • And k is /c • So we have

Sample Problem (3) An electron is trapped in a cubical infinite square well of side a in the state |2, 2, 1. Calculate the rate for spontaneous emission to fall to the ground state |1, 1, 1. • Let k be in an arbitrary direction • Choose polarizations perpendicular to k and each other • The dot products are: • Sum on polarizations: • Integrate over angles:

18 C. The Self-Energy of the Electrons • Consider effects from W(2): • This should cause a shift in energy of any atomic state • Only part that contributes is if we create and then annihilate a photon • And they must be the same photon • Energy is infinite, but independent of the atomic configuration! • Since it is constant, independent of atomic state, we can ignore it

18 D. Photon Scattering Second Order in e • We will consider situations where there is one initial photon and one final photon • We need to eliminate one photon and create one photon • Requires two factors of W(1) or one of W(2) – Both cases are second order in e • To second order, we will have: • Which states |n shall we include? • At first step, we can either delete photon k. I or create photon k. F • Hence there are only two possible intermediate photon states • The atomic state could still be anything, so • The starting energy is • The intermediate energy is • The energy denominator is:

Putting it Together • We now put it all together: • For future purposes, I will give these three pieces names

18 E. A Diagrammatic Approach • • Equations are getting complicated. Let’s draw pictures instead We’ll draw atomic states as arrows to the right and photons as squiggly lines Time will increase to the right W(1) can create one photon or annihilate one photon • W(2) can annihilate two, create two, or create and annihilate one each • We will label the atomic states by their state, and the photons by their momentum • For the process we have been discussing, it would look like this: • Can deduce what particles are present in the intermediate states from diagrams

18 F. Thomson Scattering The Electron Gains Little Energy • Consider a photon scattering from a free electron • Properly normalized eigenstates are just labeled by their momentum q: • We wish to consider: • To simplify, assume initial electron is at rest, q. I = 0 – This doesn’t change the result, but makes calculations a little simpler • We will assume photon energy is less than rest energy of electron – Otherwise we would have to treat electron relativistically • The change in photon momentum will be of order k. I • The electron’s final momentum will therefore be q. F ~ k. I • The electron’s final energy will be of order • Electron kinetic energy negligible compared to photon energy

Relative Size of TFI(1), TFI(2) and TFI(3) • Let’s look at a couple of the terms: • Because we assumed q. I = 0, P gives zero acting on q. I • The other term is order • For the other factor of W(1), we have P ~ k. I as well – This yields a comparable factor for the other W(1) • The energy denominator is order I • So we estimate: • In contrast: • Relative size of the two terms: • Similar argument can be made for the remaining term (not shown) • Bottom line: Ignore TFI(2) and TFI(3)

The Scattering Amplitude Is: • Put it all together • Substitute in the expression • This yields: • Only terms that matter must annihilate correct photon and create correct photon • Let the photon part act:

Simplifying: • The “atomic” matrix elements are easy: • Fermi’s Golden Rule • Rewrite with help of fine structure constant • We can also sum over final electron momentum q. F, which is trivial • We also can sum over the final state photon k. F and polarization F • And take the limit V

The Thomson Cross-Section • Electron kinetic energy is negligible • Note still proportional to 1/V • Trying to hit one electron with one photon • More appropriate to think in terms of cross-section: • We can add over polarizations: – Let be angle between initial polarizations and k. F • And then integrate over angles

Discussion of Thomson Scattering • Numerical value: – Much smaller than an atom • Though small, it is larger than the cross-section for a tightly bound electron • When universe was 380, 000 years old, electrons combined with protons to make hydrogen atoms – This process is called recombination • At this time, universe went from opaque to transparent – Homework problem • It is possible to obtain the same expression classically

18 G. Scattering Away from Resonance Setting it Up • Consider a photon scattering from electrons bound in an atom • We will assume the final atomic state matches the initial atomic state – This also assures that final frequency matches original, I = F = • We will generally assume we are starting in the ground state • We will assume that we are not near resonance • Recall that we had a complicated expression: • We gave them names

The Term TFI(1) • Start with TFI(1): • Need to write this out • Must annihilate state k. I and create state k. F – Two terms contribute • Let photon part act • We want photons whose energy is comparable or less than the binding energy of the atom • This means wavelength much longer than the atom, k R << 1

The Term TFI(2): The Dipole Approximation • Now for TFI(2): • Need to substitute: • We argued a long time ago that typically A P is larger than B S • Write out A: • For example, for the second factor, we must annihilate k. I, so only one term counts: • Let the photon operators act • And approximate k Rj = 0 • And the sum on Pj is P

The Term TFI(2): Putting it Together • • The other factor is similar We can write Put it all together: We can take 0 because not near zero • Turns out it is useful to rewrite the denominator

The Term TFI(2): Clever Rewriting • A clever identity we have used before: • Substitute this for the first factor, and for the first term on the second factor: • On the first term, note that we have a complete sum over intermediate states • For the last term, simplify a little: • So we have:

The Term TFI(3): Done Fast and Dirty • Now for TFI(3), take limit 0 from the start • Substitute for W(1): • • Dipole approximation: Ignore B and ignore eik r Rewrite We now have: Rewrite the denominator

Finishing TFI(3) • Our clever identity again: • Make this replacement on the second factor, and on the first factor second term • First term has a sum over complete states • On second term, simplify using • We have:

Putting the Pieces Together • Add all the pieces together • To simplify a bit, let’s assume real polarizations or real dipole moments

A Lucky Cancellation • The second term is a commutator: • This cancels exactly the first term! • Simplify the remaining term: • Hard (in general) to use this formula because there is still an infinite sum • If we are close, but not too close to resonance, we can estimate by keeping only one term

Tightly Bound Electron vs. Free Electron • Scale of an atom: • Characteristic electron “velocity”: • Order of magnitude for bound electron: • Recall for Thomson cross-section: • Cross section is proportional to |T |2, so • If electron is tightly bound, << n. I • Tightly bound atom much more transparent than free electron

Sample Problem An electron is trapped in a cubical infinite square well of side a in the ground state. Calculate the cross section for scattering of a photon polarized in the z-direction, if it has frequency • • • Eigenstates: Ground state is 1, 1, 1 Eigenstates are orthogonal: We need to find Vanishes unless n = p = 1 • For these states, only the z-component of rn. I exists

Sample Problem (2) An electron is trapped in a cubical infinite square well of side a in the ground state. Calculate the cross section for scattering of a photon polarized in the z-direction, if it has frequency • Summing over all states is just • The energies are: • Therefore, the frequency differences are: • So we have

Sample Problem (3) An electron is trapped in a cubical infinite square well of side a in the ground state. Calculate the cross section for scattering of a photon polarized in the z-direction, if it has frequency • Call the sum S: • Use Fermi’s Golden Rule: • Sum over all final states. Take limit V and turn the sum into an integral

Sample Problem (4) An electron is trapped in a cubical infinite square well of side a in the ground state. Calculate the cross section for scattering of a photon polarized in the z-direction, if it has frequency • Use the fine structure constant: • We use the standard method to convert to cross section: • Numerically (with the help of Maple): • So we have: • Compare to:

18 G. Scattering Near a Resonance We Have to be Careful! • If you simply use the transition matrix formula we got before, you will get infinity if you let = n. I for any n • If you look at the computation, it is easy to see that this comes from TFI(2) • Look at our diagrams to see what is happening: • Photon has just the right energy to match intermediate state energy

Focusing on the Problem • Let’s assume we are very close to resonance, n. I for some n • To simplify, assume there is just one n that causes this – You can redefine intermediate states, if necessary, to make this true • Since it’s large, keep only TFI(2), and only one term in the sum • Use our usual trick: • Call the resulting expression TFI(0) – Because later we will add extra loops, and this one has zero loops • Do not take 0 too early!

A Quick Reminder: • Recall: • At each order, you get: – Another factor W in the numerator – An energy denominator of EI – En + i

Making a Bad Problem Worse … • One intermediate n state made the transition matrix large • How about this diagram with two intermediate states n? What additional factors does this have compared to TFI(0) in the denominator? • For each new intermediate state, get an extra factor of EI – En + i • So we have two new factors in the denominator: What additional factors does this have compared to TFI(0) in the numerator? • Each interaction has a new W(1) matrix element • So our new term, compared to old, is: • This makes it even larger

Simplifying the New Expression • We want to work out our matrix elements using • We will make the usual dipole approximation k R = 0, and ignore spin term • We use our common trick • So we have:

Sum Over Intermediate Photon States • We are supposed to sum over intermediate states • Take the limit V • Fine structure constant • Spherical coordinates • Do the sum on spins and the angular integrals • Replace k = k/c

Separating Into Real and Imaginary Parts • Define the real and imaginary part of the expression as: • Keep in mind there is an implied limit 0+ • The real part doesn’t really interest us – It looks infinite, but isn’t – This is from high frequency, where we incorrectly ignored the eik R • • The imaginary part is what is going to save us Im( k) Look at the complex k plane Note there is a pole at We are integrating along the real axis k Re( k)

Finding the Imaginary Part • We can take the limit we distort the path of integration appropriately • The only part that contributes is the little hop near • We write k = – ei with from 0 to 0+ if Im( k) • Recall that we are assumed to be near resonance, so n. I • This is exactly the same as the decay rate for (n I)! – And this is not a coincidence k Re( k)

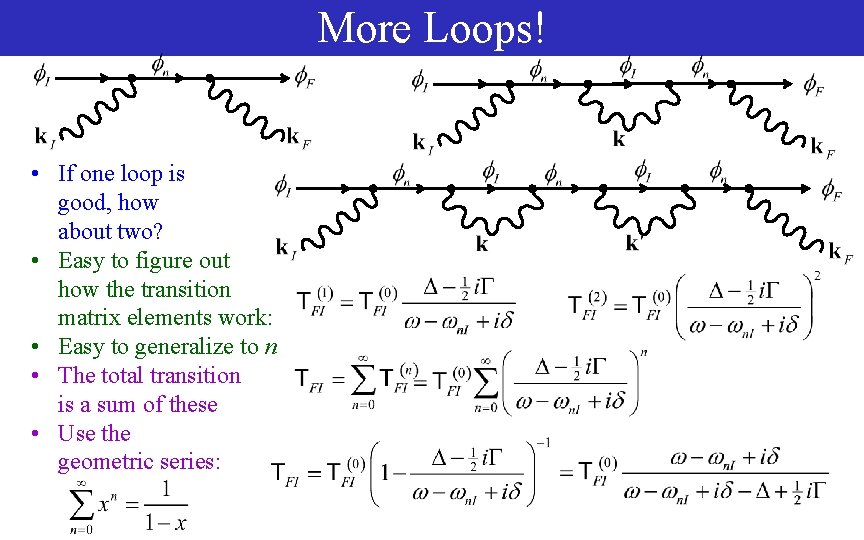
More Loops! • If one loop is good, how about two? • Easy to figure out how the transition matrix elements work: • Easy to generalize to n • The total transition is a sum of these • Use the geometric series:

And Now the Magic Happens • • Recall: Combine them Note that we can now take limit 0! The presence of the imaginary part fixes the problem, no longer a divergence We can also see the significance of : • It adds to the frequency n. I • Multiply by – Recalling that n. I = n – I • It is effectively just a shift of the energy of state n of • We’ll normally ignore this, since it doesn’t change anything qualitatively

Finding the Cross-Section (1) • Substitute into Fermi’s Golden Rule: • • Use fine structure constant: Sum over all final state polarizations and momenta Take limit V We now have: • Rewrite in spherical coordinates

Finding the Cross-Section (2) • Do the sum over polarizations and the integral over angles • Do the remaining integral • Still proportional to 1/V • We need to convert to a cross-section • So the cross-section is

A Slight Simplification • We assumed there is only one state n at this energy • If there are multiple ones, they are generally rotationally related to each other • By judicious choice of basis n, we can make it so one of them has rn. I in the direction of the polarization, and the rest are zero, so • We therefore have: • For reference, recall:

Comments on Scattering Cross-Sections • On resonance, = n. I, scattering can be enormous • Compare ~ 100 nm vs. a 0 ~ 0. 1 nm • We pretended that the state resulting from decay was only I – If there are other states, we must use the total decay rate for • We did all calculations in dipole approximation, but qualitatively results are the same • The cross-section with this characteristic form is called a Lorentzian line shape

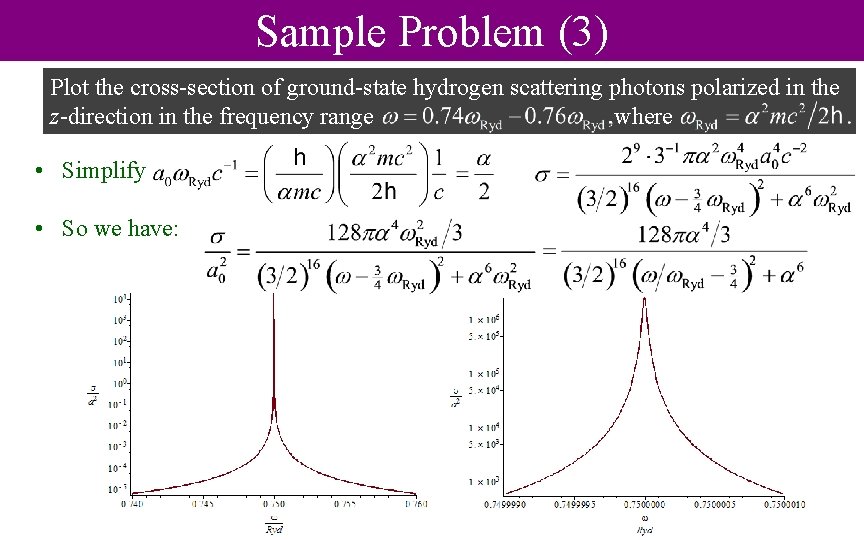
Sample Problem Plot the cross-section of ground-state hydrogen scattering photons polarized in the z-direction in the frequency range where • • • The energies of the eigenstates of hydrogen are Thus, the energy to go from n = 1 to n = 2 is 0. 75 Ryd We first need to find the matrix element: We know this vanishes unless l = 1 It is not hard to show for m = 1, we have Therefore, the only relevant state is |210 , for which

Sample Problem (2) Plot the cross-section of ground-state hydrogen scattering photons polarized in the z-direction in the frequency range where • If we replace Z by X or Y, we have • Therefore • We find the decay rate: • The cross-section is then:

Sample Problem (3) Plot the cross-section of ground-state hydrogen scattering photons polarized in the z-direction in the frequency range where • Simplify • So we have:

Another Way of Thinking About Scattering • Suppose you are at/close to resonance • Then you have the right energy to absorb a photon: • It will then remain in the state | n for a typical time t = -1 • And then decays back to the state • Since it lasts a finite time, it implies there is an uncertainty • Note that the cross-section is large whenever exceeds the difference in frequencies • This implies the energy En is effectively uncertain by • We therefore have: – The energy/time uncertainty relationship

Decay as Imaginary Energy • Recall that the effects of the loops was • Cancelling and multiplying by – And using n. I = n – I • • • So we have effectively We already mentioned that is a shift in the energy Can we see as something like an imaginary energy? Imagine at t = 0 we are in state | n Then at t we will be in state • Probability of it being in state | n is then • In other words, it makes sense to think of it as imaginary energy